Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- Home
- Engineering
- Solve this problem - Co-ordinate geometry - JEE Main
The product of the perpendiculars drawn from the foci of the ellipse ,  upon the tangent to it at the point
upon the tangent to it at the point
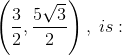
- Option 1)
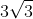
- Option 2)
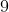
- Option 3)
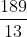
- Option 4)
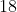
- Option 1)
- Option 2)
- Option 3)
- Option 4)
Answers (1)

As learnt in
Foci of Ellipse -
The two fixed points on the ellipse.
- wherein
Product of perpendicular drawn from foci is always = b2
In ellipse ;
Hence product =9
Option 1)
This option is incorrect.
Option 2)
This option is correct.
Option 3)
This option is incorrect.
Option 4)
This option is incorrect.
View full answer
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Similar Questions
- 0.27 g of a long chain fatty acid was dissolved in 100 cm3 of hexane. 10 mL of this solution was added dropwise to the surface of water in a
- 0.3 g of acid is neutralised by 40 cm3 .125N NaOH .equvivalent mass of acid is
- 1. A block of mass 10 kg is kept on a rough inclined as shown in figure. The coefficient of friction between the block and the surface is 0


