Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • The mean and variance of 20 observations are found to be 10 and 4, respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then the correct variance is :Option: 1 <img alt="4.01" src="h

The mean and variance of 20 observations are found to be 10 and 4, respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then the correct variance is :
Option: 1 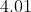4.01
Option: 2 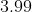3.99
Option: 3 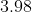3.98
Option: 4 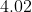4.02

Answers (1)

best_answer

 

 

Dispersion (Variance and Standard Deviation) -

Variance and Standard Deviation

The mean of the squares of the deviations from the mean is called the variance and is denoted by σ2 (read as sigma square).

Variance is a quantity which leads to a proper measure of dispersion. 

The variance of n observations x1 , x2 ,..., xn is given by

\sigma^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}

Standard Deviation

The standard deviation is a number that measures how far data values are from their mean.

The positive square-root of the variance is called standard deviation. The standard deviation, usually denoted by σ  and it is given by

\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}


Variance and Standard Deviation of a Discrete Frequency Distribution

The given discrete frequency distribution be

         \begin{matrix} x &: &x_1, & x_2, & x_3, &\ldots &x _n & \\ & & & & & & & \\ f& : & f_1, &f_2, &f_3, &\ldots & f_n & \end{matrix}

\\\text{In this case, Variance}\;\left ( \sigma^2 \right ) \;\;\;=\frac{1}{N} \sum_{i=1}^{n} f_{i}\left(x_{i}-\bar{x}\right)^{2}\\\\\text{and, Standard Deviation}(\sigma)\;=\sqrt{\frac{1}{N} \sum_{i=1}^{n} f_{i}\left(x_{i}-\bar{x}\right)^{2}}\\\text{where, N}=\sum_{i=1}^{n} f_{i}

 

Variance and Standard deviation of a continuous frequency distribution 

The formula for variance and standard deviation are the same as in the case of discrete frequency distribution. Here, x_i is the mid point of each class.

 

Another formula for Standard Deviation

\\\text{Variance }\left ( \sigma^2 \right )=\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i}\left(x_{i}^{2}+\bar{x}^{2}-2 \bar{x} x_{i}\right)\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{N}\left[\sum_{i=1}^{n} f_{i} x_{i}^{2}+\sum_{i=1}^{n} \bar{x}^{2} f_{i}-\sum_{i=1}^{n} 2 \bar{x} f_{i} x_{i}\right]\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{N}\left[\sum_{i=1}^{n} f_{i} x_{i}^{2}+\bar{x}^{2} \sum_{i=1}^{n} f_{i}-2 \bar{x} \sum_{i=1}^{n} x_{i} f_{i}\right]\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{N}\left[\sum_{i=1}^{n} f_{i} x_{i}^{2}+\bar{x}^{2} N-2 \bar{x} \cdot N\bar x\right]

\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{N}\left[\sum_{i=1}^{n} f_{i} x_{i}^{2}+\bar{x}^{2} N-2 \bar{x} \cdot N\bar x\right]\\\\\left [ \because \frac{1}{N} \sum_{i=1}^{n} x_{i} f_{i}=\bar{x} \text { or } \sum_{i=1}^{n} x_{i} f_{i}=\mathrm{N} \bar{x} \right ]\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i} x_{i}^{2}+\bar{x}^{2}-2 \bar{x}^{2}=\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i} x_{i}^{2}-\bar{x}^{2}\\\\\text{or}\;\;\sigma^{2}=\frac{1}{N} \sum_{i=1}^{n} f_{i} x_{i}^{2}-\left(\frac{\sum_{i=1}^{n} f_{i} x_{i}}{N}\right)^{2}=\frac{1}{N^{2}}\left[N \sum_{i=1}^{n} f_{i} x_{i}^{2}-\left(\sum_{i=1}^{n} f_{i} x_{i}\right)^{2}\right]

\text{Thus, standard deviation }(\sigma)=\frac{1}{N} \sqrt{N \sum_{i=1}^{n} f_{i} x_{i}^{2}-\left(\sum_{i=1}^{n} f_{i} x_{i}\right)^{2}}



Shortcut method to find variance and standard deviation

The values of x_i  in a discrete distribution or the mid points x_i of different classes in a continuous distribution are large and so the calculation of mean and variance becomes tedious and time consuming.

Here is the shortcut method to find variance and standard deviatio

Let the assumed mean be ‘A’ and the scale be reduced to 1/h times (h being the width of class-intervals). 

Let the step-deviations or the new values be y_i .

\\\text { i.e. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \quad y_{i}=\frac{x_{i}-\mathrm{A}}{h} \text { or } x_{i}=\mathrm{A}+h y_{i}|\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ldots(1)\\\\\text { We know that } \quad\;\;\;\;\;\bar x= \frac{\sum_{i=1}^{n} f_{i} x_{i}}{N}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ldots(2)

Replacing x_i from (1) in (2), 

 

\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\bar{x}=\frac{\sum_{i=1}^{n} f_{i}\left(\mathrm{A}+h y_{i}\right)}{\mathrm{N}}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\frac{1}{\mathrm{N}}\left(\sum_{i=1}^{n} f_{i} \mathrm{A}+\sum_{i=1}^{n} h f_{i} y_{i}\right)=\frac{1}{\mathrm{N}}\left(\mathrm{A} \sum_{i=1}^{n} f_{i}+h \sum_{i=1}^{n} f_{i} y_{i}\right)\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\mathrm{A} \cdot \frac{\mathrm{N}}{\mathrm{N}}+h \frac{\sum_{i=1}^{n} f_{i} y_{i}}{\mathrm{N}} \quad\left(\text { because } \sum_{i=1}^{n} f_{i}=\mathrm{N}\right)\\\text { Thus } \quad \bar{x}=\mathrm{A}+h \bar{y}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ldots(3)
Now Variance of the variable x

\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\sigma_{x}^{2}=\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i}\left(x_{i}-\bar{x}\right)^{2}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} =\frac{1}{\mathrm{N}} \sum_{i=1}^{n} f_{i}\left(\mathrm{A}+h y_{i}-\mathrm{A}-h \bar{y}\right)^{2}\;\;\;\;\;\;\;\;\;\text{(Using (1) and (3))}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} =\frac{1}{N} \sum_{i=1}^{n} f_{i} h^{2}\left(y_{i}-\bar{y}\right)^{2}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} =\frac{h^{2}}{\mathrm{N}} \sum_{i=1}^{n} f_{i}\left(y_{i}-\bar{y}\right)^{2}=h^{2} \times \text { variance of the variable } y_{i}\\\text { i.e. }\;\;\;\; \quad \sigma_{x}^{2}=h^{2} \sigma_{y}^{2}\;\;\\\text { or }\;\;\;\;\;\; \quad \sigma_{x}=h \sigma_{y}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ldots(4)

From (3) and (4),

\sigma_{x}=\frac{h}{\mathrm{N}} \sqrt{\mathrm{N} \sum_{i=1}^{n} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{n} f_{i} y_{i}\right)^{2}}

-

 

\\\\\sigma_{new}^2=4-\left [\frac{(11-9)}{20} \right ]^2=4-\frac{4}{200}=3.99

Correct Option (2)

Posted by

vishal kumar

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2025 registration ends tomorrow; changes introduced in exam this year
anam-khan

BTech Admission 2025 Live: JEE Mains registrations closing tomorrow; VITEEE, MET exam dates out
anam-khan

JEE Main 2025 Live: NTA to close JEE registration on Friday; apply at jeemain.nta.nic.in, correction window

Latest Question