Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • The temperature of equal masses of three ifferent liquids x,y and z are <img alt="10^{\circ}C,20^{\circ}C \, and\, 30^{\circ}C" src="https://entrancecorner.codecogs.com/gif.latex?10%5E%7B%5Ccirc%7DC%2C20%5E%7B%5Ccirc%7DC%20%5C%2C%20and%5C%2C%2030%5E%7B%5C

The temperature of equal masses of three ifferent liquids x,y and z are 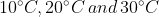10^{\circ}C,20^{\circ}C \, and\, 30^{\circ}C respectively.The temperature of mixture when x is mixed with y is 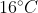16^{\circ}C and that when y is mixed with z is 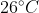26^{\circ}C, The temperature of mixture when x and z are mixed will be :
 
Option: 1 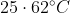25\cdot 62^{\circ}C
Option: 2 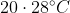20\cdot 28^{\circ}C
Option: 3 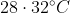28\cdot 32^{\circ}C
Option: 4 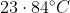23\cdot 84^{\circ}C

Answers (1)

best_answer

T_{mix}= \frac{n_{1}T_{1}+n_{2}T_{2}}{n_{1}+n_{2}}
T_{x}= 10^{\circ}C= 283\, k
T_{y}= 20^{\circ}C= 293\, k
T_{z}= 30^{\circ}C= 303\, k
For x & y mixture ,
T_{1}= \frac{n_{x}T_{x}+n_{y}T_{y}}{n_{x}+n_{y}}
289= \frac{\frac{m_{x}T_{x}}{M_{x}}+\frac{m_{y}T_{y}}{M_{y}}}{\frac{m_{x}}{M_{x}}+\frac{m_{y}}{M_{y}}}
289= \frac{\frac{283}{M_{x}}+\frac{293}{M_{y}}}{\frac{1}{M_{x}}+\frac{1}{M_y}}\rightarrow \left ( 1 \right )
Mixture of y & Z
299= \frac{\frac{293}{M_{y}}+\frac{303}{M_{z}}}{\frac{1}{M_{y}}+\frac{1}{M_z}}\rightarrow \left ( 2 \right )
Mixture of x & z
T_{3}= \frac{\frac{283}{M_{x}}+\frac{303}{M_{z}}}{\frac{1}{M_{x}}+\frac{1}{M_z}}\rightarrow \left ( 3 \right )
From eqn (1)
\frac{289}{M_{x}}+\frac{289}{M_{y}}= \frac{283}{M_{x}}+\frac{213}{M_{y}}
6M_{y} = 4M_{x}
3M_{y} = 2M_{x}\rightarrow \left ( 4 \right )
6M_{z} = 4M_{y}
3M_{z} = 2M_{y}\rightarrow \left ( 5 \right )
3\times \frac{3M_{z}}{2} = 2M_{x}
9 M_{z} = 4M_{x}\rightarrow \left (6 \right )
T_{3}= \frac{\frac{283}{\frac{9}{4}M_{z}}+\frac{303}{M_{z}}}{\frac{1}{\frac{9}{4}M_{z}}+\frac{1}{M_{z}}}= \frac{\frac{4\times 283}{9}+\frac{303\times 9}{9}}{\frac{4}{9}+\frac{9}{9}}
= \frac{4\times283+303\times9}{13}= 296\cdot 84 k
T_{3}= 23\cdot 84\degree C
The correct option is (4)

Posted by

vishal kumar

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

Amrita BTech Admission 2025: JEE Main-based registration deadline extended to August 30
anam-khan

DASA, CSAB Special round 2 seat allotment result 2025 declared on csab.nic.in

Latest Question