Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • Which of the following statements is a tautology ?Option: 1  

Which of the following statements is a tautology ?
Option: 1 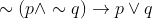\sim (p\wedge \sim q)\rightarrow p\vee q  
Option: 2 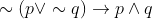\sim (p\vee \sim q)\rightarrow p\wedge q
Option: 3 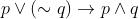p\vee (\sim q)\rightarrow p\wedge q
Option: 4 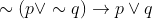\sim (p\vee \sim q)\rightarrow p\vee q

Answers (1)

best_answer

 

 

Tautology And Contradiction -

Tautology

A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example,    ( p ⇒ q ) ∨ ( q ⇒ p ) 

 

Contradiction (fallacy)

A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p ) 

 

Truth Table

\begin{array}{|c|c|c|c|c|c|c|c|}\hline \mathrm{\;\;\;\;\;}p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}q\mathrm{\;\;\;}&\mathrm{\;\;\;\;\;}p\rightarrow q\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;} q\rightarrow p\mathrm{\;\;\;} &\mathrm{\;\;\;}\left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right )\mathrm{\;\;}&\mathrm{\;\;\;}\sim\left ( \left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right ) \right ) \mathrm{\;\;} \\\hline \hline \mathrm{T}&\mathrm{T} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{T}&\mathrm{F} & \mathrm{F} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{T} & \mathrm{T} &\mathrm{F}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{F} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline\end{array}

Quantifiers

Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases. 

For example – 

p : For every prime number x, √x is an irrational number.

q : There exists a triangle whose all sides are equal.

-

 

 

 

Practise Session - 1 -

Q1. Write the negations of the following:
      1. Ram is a doctor or peon.
      2. Room is clean and big.
      3.\sqrt 5 is a rational number.
      4. If Ram is a doctor then he is smart

 

 

-

 

 

 

 

\sim(p \vee \sim q) \rightarrow p \vee q

\begin{array}{l}{(\sim p \wedge q) \rightarrow(p \vee q)} \\ {\sim\{(\sim p \wedge q) \wedge(\sim p \wedge \sim q)\}} \\ {\sim\{\sim p \wedge f\}}\end{array}

Correct Option (4)

Posted by

vishal kumar

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2024: NTA debars 39 candidates for 3 years on account of using unfair means
anam-khan

JEE Main 2024 session 2 paper 2 answer key objection window closes today; fees
anam-khan

JEE Main 2024 Topper: Farmer’s son Gajare Nilkrishna says ‘keep questioning until you understand’

Latest Question