Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Management
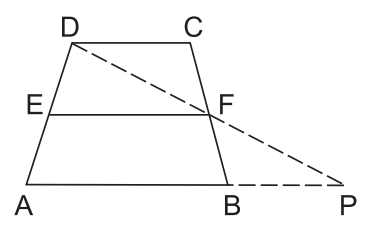
  • In trapezium ABCD, E and F are the midpoints of sides AD and BC respectively. Then which of the following is true <img alt="" src="https://cdn.entrance360.com/media/uploads

In trapezium ABCD, E and F are the midpoints of sides AD and BC respectively. Then which of the following is true

Option: 1

EF || AB


Option: 2

E F=\frac{1}{2}(A B+C D)


Option: 3

2EF = AB


Option: 4

Both (a) and (b)


Answers (1)

best_answer

Join DF and produce it to meet AB produced in P

In triangle DCF and PBF we have

∠DFC = ∠PFB   (vertically opposite angle)

BF = FC   (F is mid point of BC)

∠DCF = ∠PBF    (alternate interior angle)

? DCF ≅ ? PBF

therefore, DF = PF and  CD = BP

Now in triangle, DAP

E is the midpoint of AD and F is the midpoint of DP.

\\ \therefore \quad E F \| A P \text { and } E F=\frac{1}{2} A P \quad[ \text { mid point theorem} \\ \Rightarrow \quad E F \| A B \text { and } E F=\frac{1}{2}(A B+B P) \\

Posted by

Ajit Kumar Dubey

View full answer

Similar Questions

Latest Question