Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Edited By Dinesh Goyal | Updated on Sep 04, 2023 08:55 PM IST | #CBSE Class 10th

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables are discussed here. Class 10 Maths chapter 3 is an important chapter of Algebra and this chapter are created by expert team at careers360 keeping in mind of latest CBSE syllabus 2023. In Class 10 Maths chapter 3 solutions, students will learn to solve the linear equation with two variables. Class 10 Maths chapter 3 NCERT solutions contain the answers of all exercise NCERT questions.

This Story also Contains
  1. NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
  2. Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables PDF Free Download
  3. Pair of Linear Equations in Two Variables Class 10- Important Formulae
  4. NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables (Intext Questions and Exercise)
  5. Key Features of NCERT Class 10 Maths Solutions Chapter 3
  6. NCERT Books and NCERT Syllabus
  7. NCERT Solutions of Class 10 - Subject Wise
  8. NCERT Exemplar solutions - Subject wise
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

NCERT Class 10 Maths chapter 3 solutions are helpful to know the answers to the questions asked in NCERT class 10 maths book. Apart from this, by going through NCERT solutions for class 10 maths chapter 3, they will come to know about various methods of solving questions. NCERT solutions for class 10 are also available for other subjects.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

Also read,

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables PDF Free Download

Download PDF

Pair of Linear Equations in Two Variables Class 10- Important Formulae

Types of Linear Equations:

S. No.

Types of Linear Equation

General form

Description

Solutions

1.

Linear Equation in one Variable

ax + b = 0

Where a ≠ 0 and a & b are real numbers

One Solution

2.

Linear Equation in Two Variables

ax + by + c = 0

Where a ≠ 0 & b ≠ 0 and a, b & c are real numbers

Infinite Solutions possible

3.

Linear Equation in Three Variables

ax + by + cz + d = 0

Where a ≠ 0, b ≠ 0, c ≠ 0 and a, b, c, d are real numbers

Infinite Solutions possible

Simultaneous System of Linear Equations: A pair of equations in the format:

a1x + b1y + c1 = 0

a2x + b2y + c2 = 0

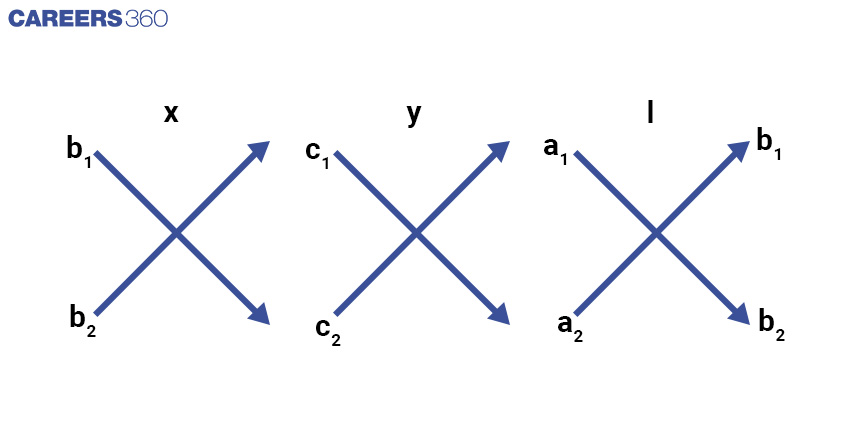
This arrangement is visually depicted through the use of two straight lines on the Cartesian plane, as explained in the following context:

1693838268417

When there is a unique solution then

x/(b1c2 - b2c1) = y/(c1a2 - c2a1) = 1/(a1b2 - a2b2)

This formula can be remembered as the diagram given below

1693838268800

Free download NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables (Intext Questions and Exercise)

Class 10 Maths Chapter 3 solutions Pair of Linear Equations in two variables Excercise: 3.1

Q1 Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.

Answer: Let x be the age of Aftab and y be the age of his daughter

Now, According to the question,

(x-7)=7\times(y-7)

\Rightarrow x-7=7y-49

\Rightarrow x-7y=-42.....(1)

Also,

(x+3)=3(y+3)

\Rightarrow x+3=3y+9

\Rightarrow x-3y=6.....(2)

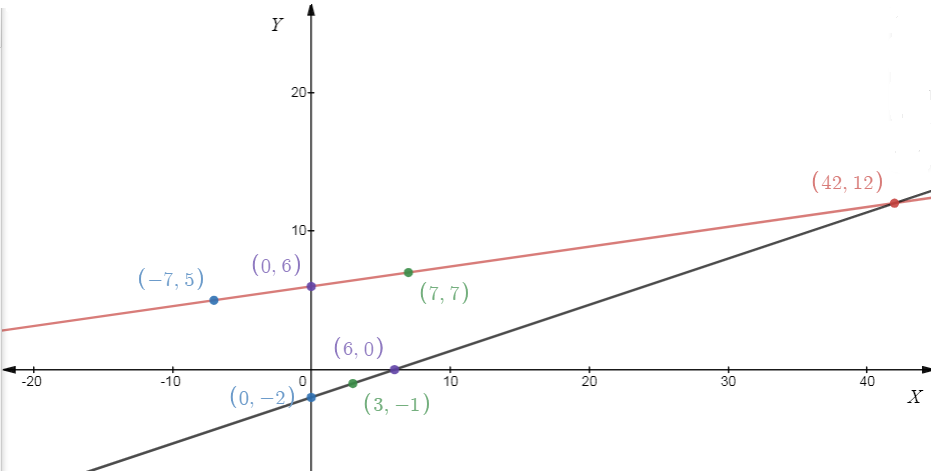
Now, let's represent both equations graphically,

From (1), we get

y=\frac{x+42}{7}

So, Putting different values of x we get corresponding values of y

X

0

7

-7

Y

6

7

5


And From (2) we get,

y=\frac{x-6}{3}

So, Putting different values of x we get corresponding values of y

X

0

3

6

Y

-2

-1

0

GRAPH:

Graph X-Y

Q2 The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.

Answer:

Let the price of one Bat be x and the price of one ball be y,

Now, According to the question,

3x+6y=3900.....(1)

x+3y=1300.....(2)

From(1) we have

y=\frac{3900-3x}{6}

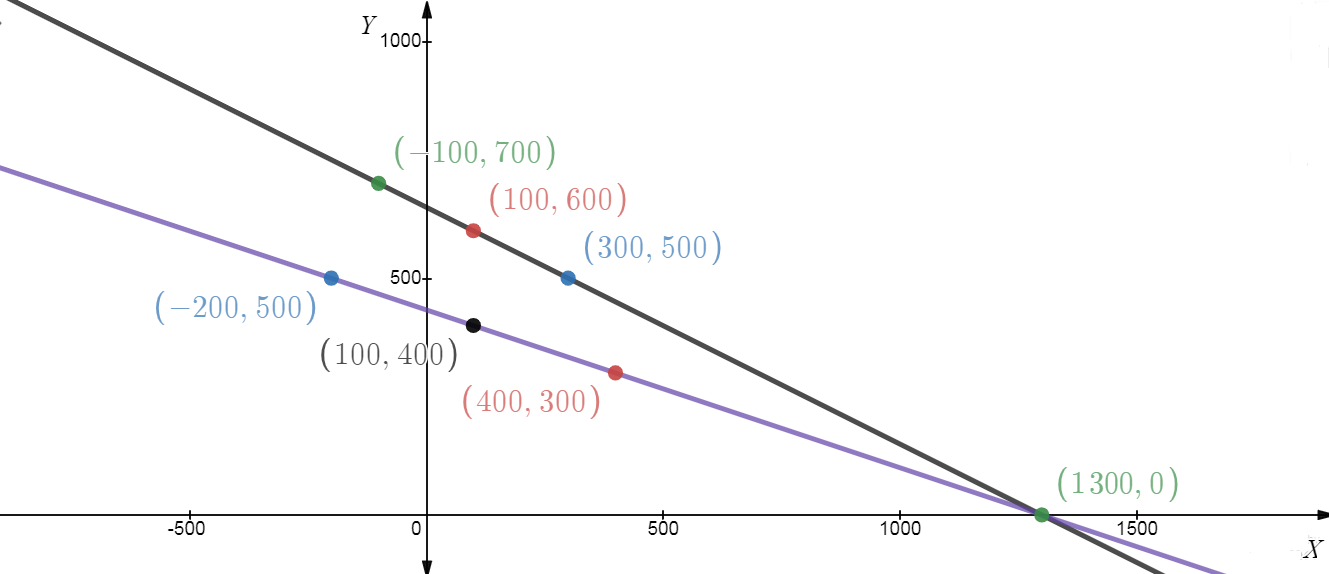
By putting different values of x, we get different corresponding values of y.So

X
100
300
-100
Y
600
500
700

Now, From (2), we have,

y=\frac{1300-x}{3}

By putting different values of x, we get different corresponding values of y.So

X
100
400
-200
Y
400
300
500

GRAPH:

1635919652158

Q3 The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.

Answer:

Let, x be the cost of 1kg apple and y be the cost of 1kg grapes.

Now, According to the question,

On a day:

2x+y=160.....(1)

After One Month:

4x+2y=300.....(2)

Now, From (1) we have

y=160-2x

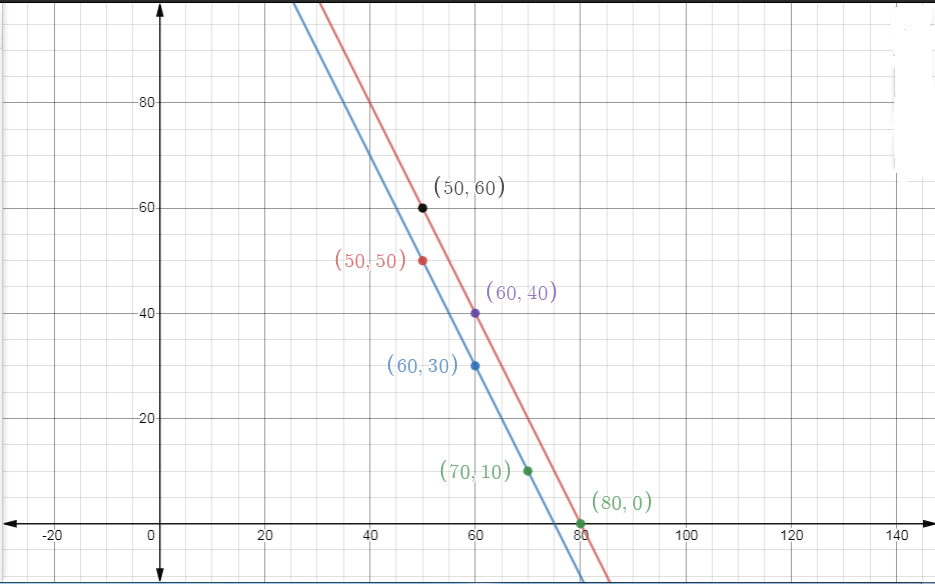
Putting different values of x we get corresponding values of y, so,'

X

80

60

50

Y

0

40

60


And From (2) we have,

y=\frac{300-4x}{2}=150-2x

Putting different values of x we get corresponding values of y, so,

X

50

60

70

Y

50

30

10

Graph:

graph


Class 10 Maths Chapter 3 solutions Pair of Linear Equations in Two Variables Excercise: 3.2

Q1 Form the pair of linear equations in the following problems and find their solutions graphically.

(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

Answer:

Let the number of boys is x and the number of girls is y.

Now, According to the question,

Total number of students in the class = 10, i.e.

\Rightarrow x+y=10.....(1)

And

the number of girls is 4 more than the number of boys,i.e.

x=y+4

\Rightarrow x-y=4..........(2)

Different points (x, y) for equation (1)

X
5
6
4
Y
5
4
6

Different points (x,y) satisfying (2)

X
5
6
7
y
1
2
3


Graph,

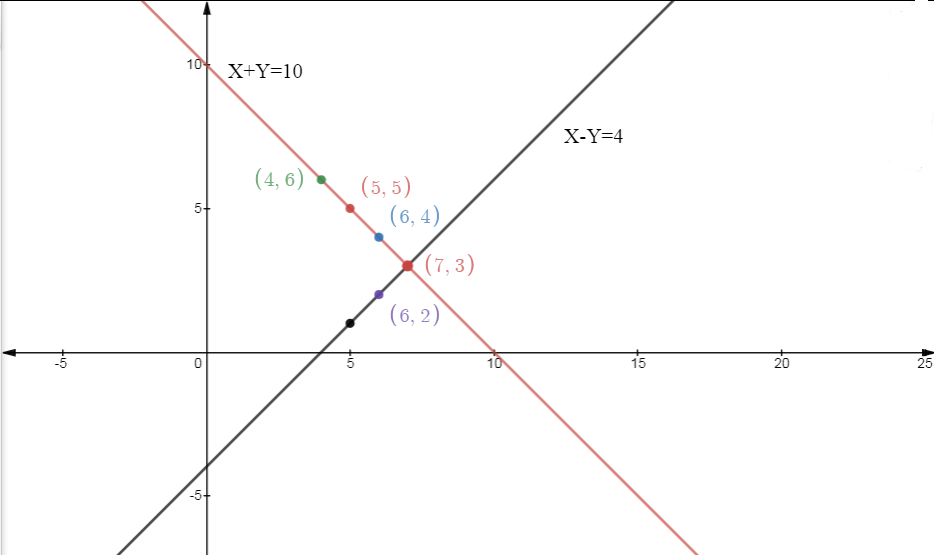
1635919752095

As we can see from the graph, both lines intersect at the point (7,3). that is x= 7 and y = 3 which means the number of boys in the class is 7 and the number of girls in the class is 3.

Q1 Form the pair of linear equations in the following problems and find their solutions graphically.

(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.

Answer:

Let x be the price of 1 pencil and y be the price of 1 pen,

Now, According to the question

5x+7y=50......(1)

And

7x+5y=46......(2)

Now, the points (x,y), that satisfies the equation (1) are

X
3
-4
10
Y
5
10
0

And, the points(x,y) that satisfies the equation (2) are

X
3
8
-2
Y
5
-2
12

The Graph,

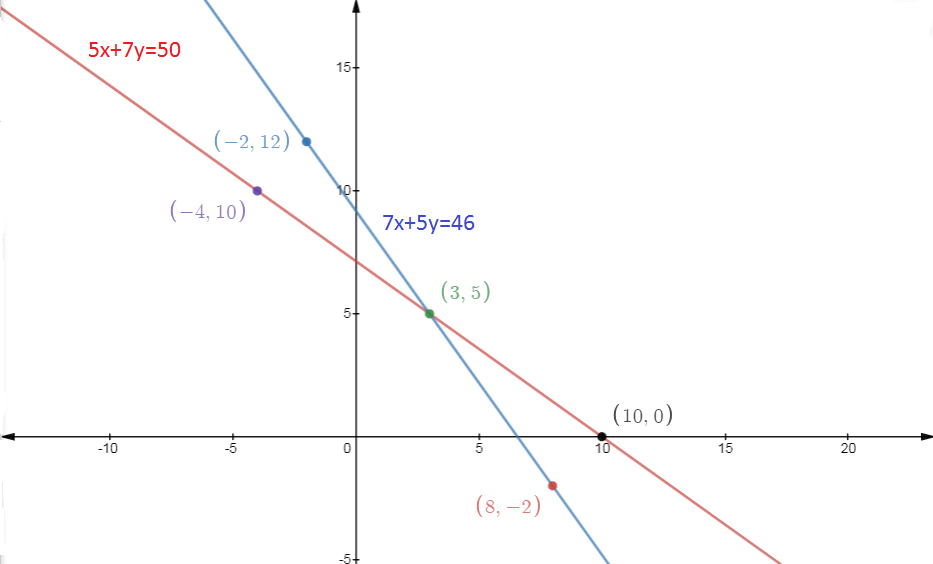
Graph

As we can see from the Graph, both line intersects at point (3,5) that is, x = 3 and y = 5 which means cost of 1 pencil is 3 and the cost of 1 pen is 5.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (i) \\5x - 4y + 8 = 0\\ 7x + 6y - 9 = 0

Answer:

Give, Equations,

\\5x - 4y + 8 = 0\\ 7x + 6y - 9 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{5}{7},\:\frac{b_1}{b_2}=\frac{-4}{6}\:and\:\frac{c_1}{c_2}=\frac{8}{-9}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means that both lines intersect at exactly one point.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (ii) \\9x + 3y + 12 = 0\\ 18x + 6y + 24 = 0

Answer:

Given, Equations,

\\9x + 3y + 12 = 0\\ 18x + 6y + 24 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}\:and \\\:\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means that both lines are coincident.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2} , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (iii) \\6x - 3y + 10 = 0\\ 2x - y+ 9 = 0

Answer:

Give, Equations,

\\6x - 3y + 10 = 0\\ 2x - y+ 9 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{6}{2}=3,\:\frac{b_1}{b_2}=\frac{-3}{-1}=3\:and\:\frac{c_1}{c_2}=\frac{10}{9}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means that both lines are parallel to each other.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (i) 3x + 2y = 5;\qquad 2x - 3y = 7

Answer:

Give, Equations,

\\3x + 2y = 5;\qquad\\ 2x - 3y = 7

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{3}{2},\:\frac{b_1}{b_2}=\frac{2}{-3}\:and\:\frac{c_1}{c_2}=\frac{5}{7}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (ii) 2x - 3y = 8;\qquad 4x - 6y = 9

Answer:

Given, Equations,

\\2x - 3y = 8;\qquad \\4x - 6y = 9

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{8}{9}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iii) \frac{3}{2}x + \frac{5}{3}y = 7;\qquad 9x -10y = 14

Answer:

Given, Equations,

\\\frac{3}{2}x + \frac{5}{3}y = 7;\qquad\\ \\ 9x -10y = 14

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{3/2}{9}=\frac{3}{18}=\frac{1}{6},\\\:\frac{b_1}{b_2}=\frac{5/3}{-10}=\frac{5}{-30}=-\frac{1}{6}\:and\\\:\frac{c_1}{c_2}=\frac{7}{14}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iv) 5x - 3y = 11;\qquad -10x + 6y =-22

Answer:

Given, Equations,

5x - 3y = 11;\qquad \\-10x + 6y =-22

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{5}{-10}=-\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{11}{-22}=-\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the following pair of linear equations are consistent, or inconsistent (v) \frac{4}{3}x + 2y = 8; \qquad 2x + 3y = 12

Answer:

Given, Equations,

\\\frac{4}{3}x + 2y = 8; \qquad\\\\ 2x + 3y = 12

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{4/3}{2}=\frac{4}{6}=\frac{2}{3},\\\:\frac{b_1}{b_2}=\frac{2}{3}\:\:and\\\:\frac{c_1}{c_2}=\frac{8}{12}=\frac{2}{3}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (i) x + y = 5 \qquad 2x + 2 y = 10

Answer:

Given, Equations,

\\x + y = 5 \qquad\\ 2x + 2 y = 10

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{5}{10}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

The points (x,y) which satisfies in both equations are

X
1
3
5
Y
4
2
0

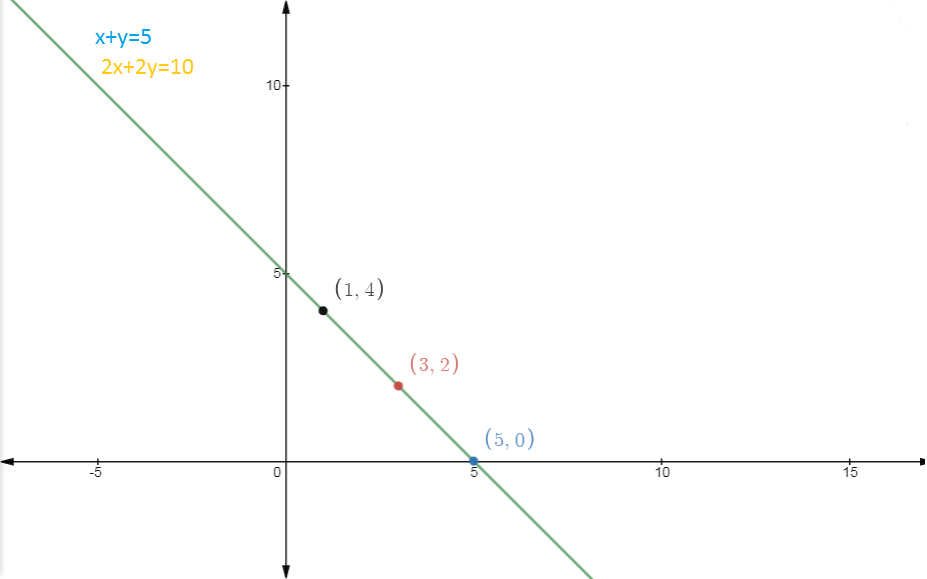
Graph

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (ii) x - y = 8,\qquad 3x - 3y = 16

Answer:

Given, Equations,

\\x - y = 8,\qquad\\ 3x - 3y = 16

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{1}{3},\\\:\frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}\:and\\\:\frac{c_1}{c_2}=\frac{8}{16}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (iii) 2x + y - 6 =0, \qquad 4x - 2 y - 4 = 0

Answer:

Given, Equations,

\\2x + y - 6 =0, \qquad \\4x - 2 y - 4 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-6}{-4}=\frac{3}{2}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Now The points(x, y) satisfying the equation are,

X
0
2
3
Y
6
2
0


And The points(x,y) satisfying the equation \\4x - 2 y - 4 = 0 are,

X
0
1
2
Y
-2
0
2


GRAPH:

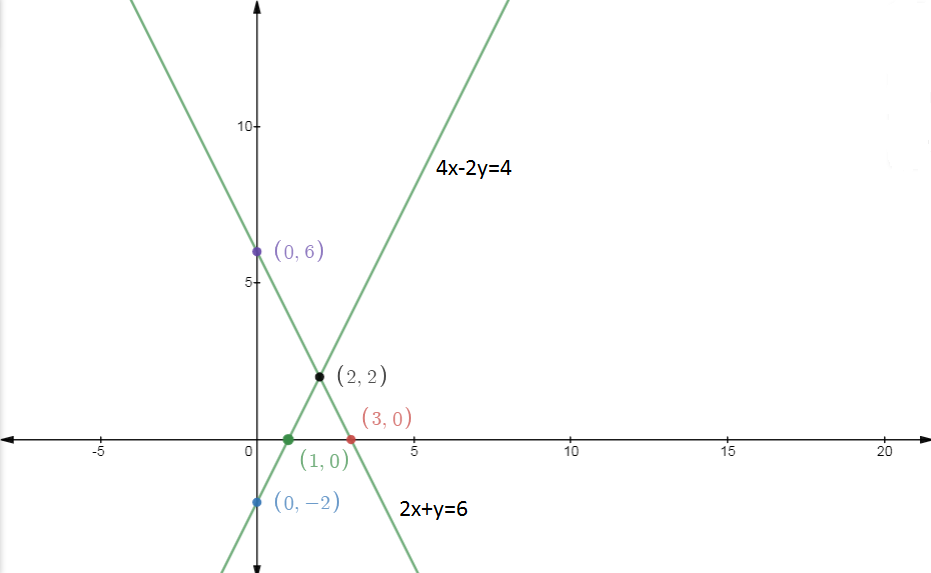
1635919975632

As we can see both lines intersects at point (2,2) and hence the solution of both equations is x = 2 and y = 2.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (iv) 2x - 2y - 2 =0, \qquad 4x - 4y -5 = 0

Answer:

Given, Equations,

\\2x - 2y - 2 =0, \qquad\\ 4x - 4y -5 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q5 Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.

Answer:

Let lbe the length of the rectangular garden and b be the width.

Now, According to the question, the length is 4 m more than its width.i.e.

l=b+4

l-b=4....(1)

Also Given Half Parameter of the rectangle = 36 i.e.

l+b=36....(2)

Now, as we have two equations, on adding both equations, we get,

l+b+l-b=4+36

\Rightarrow 2l=40

\Rightarrow l=20

Putting this in equation (1),

\Rightarrow 20-b=4

\Rightarrow b=20-4

\Rightarrow b=16

Hence Length and width of the rectangle are 20m and 16 respectively.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is: (i) intersecting lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the intersection of lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , is ,

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

So Any line with this condition can be 4x+3y-16=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{3}=1

As

\frac{1}{2}\neq1 the line satisfies the given condition.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is (ii) parallel lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , for being parallel is,

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

So Any line with this condition can be 4x+6y-8=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{-8}{-8}=1

As

\frac{1}{2}=\frac{1}{2}\neq1 the line satisfies the given condition.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is: (iii) coincident lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the coincidence of the lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , is,

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

So any line with this condition can be 4x+6y-16=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}

As

\frac{1}{2}=\frac{1}{2}=\frac{1}{2} the line satisfies the given condition.

Q7 Draw the graphs of the equations x - y + 1=0and 3x +2 y - 12=0 . Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.

Answer:

Given, two equations,

x - y + 1=0.........(1)

And

3x +2 y - 12=0.........(2)

The points (x,y) satisfying (1) are

X

0

3

6

Y

1

4

7

And The points(x,y) satisfying (2) are,

X

0

2

4

Y

6

3

0


GRAPH:

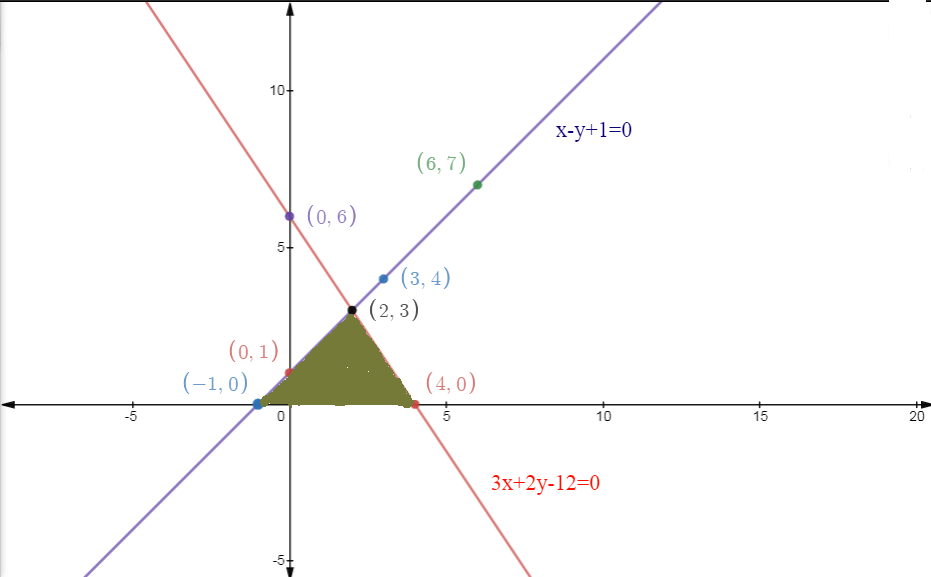
1635920037829

As we can see from the graph that both lines intersect at the point (2,3), And the vertices of the Triangle are ( -1,0), (2,3) and (4,0). The area of the triangle is shaded with a green color.

Pair of linear equations in two variables class 10 solutions Excercise: 3.3

Q1 Solve the following pair of linear equations by the substitution method. (i) \\x + y = 14\\ x - y = 4

Answer:

Given, two equations,

\\x + y = 14.......(1)\\ x - y = 4........(2)

Now, from (1), we have

y=14-x........(3)

Substituting this in (2), we get

x-(14-x)=4

\Rightarrow x-14+x=4

\Rightarrow 2x=4+14=18

\Rightarrow x=9

Substituting this value of x in (3)

\Rightarrow y=14-x=14-9=5

Hence, Solution of the given equations is x = 9 and y = 5.

Q1 Solve the following pair of linear equations by the substitution method (ii) \\s - t = 3\\ \frac{s}{3} + \frac{t}{2} = 6

Answer:

Given, two equations,

\\s - t = 3.........(1)\\ \frac{s}{3} + \frac{t}{2} = 6.......(2)

Now, from (1), we have

s=t+3........(3)

Substituting this in (2), we get

\frac{t+3}{3}+\frac{t}{2}=6

\Rightarrow \frac{2t+6+3t}{6}=6

\Rightarrow 5t+6=36

\Rightarrow 5t=30

\Rightarrow t=6

Substituting this value of t in (3)

\Rightarrow s=t+3 = 6+3=9

Hence, Solution of the given equations is s = 9 and t = 6.

Q1 Solve the following pair of linear equations by the substitution method. (iii) \\ 3 x - y = 3\\ 9x - 3y = 9

Answer:

Given, two equations,

\\ 3 x - y = 3......(1)\\ 9x - 3y = 9.....(2)

Now, from (1), we have

y=3x-3........(3)

Substituting this in (2), we get

9x-3(3x-3)=9

\Rightarrow 9x-9x+9=9

\Rightarrow 9=9

This is always true, and hence this pair of the equation has infinite solutions.

As we have

y=3x-3 ,

One of many possible solutions is x=1,\:and\:y=0 .

Q1 Solve the following pair of linear equations by the substitution method. (iv) \\0.2x + 0.3y = 1.3\\ 0.4x + 0.5y = 2.3

Answer:

Given, two equations,

\\0.2x + 0.3y = 1.3\\ 0.4x + 0.5y = 2.3

Now, from (1), we have

y=\frac{1.3-0.2x}{0.3}........(3)

Substituting this in (2), we get

0.4x+0.5\left(\frac{1.3-0.2x}{0.3}\right)=2.3

\Rightarrow 0.12x+0.65-0.1x=0.69

\Rightarrow 0.02x=0.69-0.65=0.04

\Rightarrow x=2

Substituting this value of x in (3)

\Rightarrow y=\left ( \frac{1.3-0.2x}{0.3} \right )=\left ( \frac{1.3-0.4}{0.3} \right )=\frac{0.9}{0.3}=3

Hence, Solution of the given equations is,

x=2\:and\:y=3 .

Q1 Solve the following pair of linear equations by the substitution method. (v) \\\sqrt2x + \sqrt3y = 0\\ \sqrt3x - \sqrt8y= 0

Answer:

Given, two equations,

\\\sqrt2x + \sqrt3y = 0\\ \sqrt3x - \sqrt8y= 0

Now, from (1), we have

y=-\frac{\sqrt{2}x}{\sqrt{3}}........(3)

Substituting this in (2), we get

\sqrt{3}x-\sqrt{8}\left ( -\frac{\sqrt{2}x}{\sqrt{3}} \right )=0

\Rightarrow \sqrt{3}x=\sqrt{8}\left ( -\frac{\sqrt{2}x}{\sqrt{3}} \right )

\Rightarrow \3x=-4x

\Rightarrow7x=0

\Rightarrow x=0

Substituting this value of x in (3)

\Rightarrow y=-\frac{\sqrt{2}x}{\sqrt{3}}=0

Hence, Solution of the given equations is,

x=0,\:and \:y=0 .

Q1 Solve the following pair of linear equations by the substitution method. (vi) \\\frac{3x}{2} - \frac{5y}{3}= - 2\\ \frac{x}{3} + \frac{y}{2} = \frac{13}{6}

Answer:

Given,

\\\frac{3x}{2} - \frac{5y}{3}= - 2.........(1)\\ \frac{x}{3} + \frac{y}{2} = \frac{13}{6}.............(2)

From (1) we have,

x=\frac{2}{3}\left ( \frac{5y}{3}-2 \right )........(3)

Putting this in (2) we get,

\frac{1}{3}\times\frac{2}{3}\left ( \frac{5y}{3}-2 \right )+\frac{y}{2}=\frac{13}{6}

\frac{10y}{27}-\frac{4}{9}+\frac{y}{2}=\frac{13}{6}

\frac{20y}{54}-\frac{4}{9}+\frac{27y}{54}=\frac{13}{6}

\frac{47y}{54}=\frac{13}{6}+\frac{4}{9}

\frac{47y}{54}=\frac{117}{54}+\frac{24}{54}

47y=117+24

47y=141

y=\frac{141}{47}

y=3

putting this value in (3) we get,

x=\frac{2}{3}\left ( \frac{5y}{3}-2 \right )

x=\frac{2}{3}\left ( \frac{5\times3}{3}-2 \right )

x=\frac{2}{3}\left (5-2 \right )

x=\frac{2}{3}\times 3

x=2

Hence x=2\:\:and\:\:y=3.

Q2 Solve 2x + 3y = 11and 2x - 4y = -24 and hence find the value of ‘ m’ for which y = mx + 3 .

Answer:

Given, two equations,

2x + 3y = 11......(1)

2x - 4y = -24.......(2)

Now, from (1), we have

y=\frac{11-2x}{3}........(3)

Substituting this in (2), we get

2x-4\left ( \frac{11-2x}{3} \right )=-24

\Rightarrow 6x-44+8x=-72

\Rightarrow 14x=44-72

\Rightarrow 14x=-28

\Rightarrow x=-2

Substituting this value of x in (3)

\Rightarrow y=\left ( \frac{11-2x}{3} \right )=\frac{11-2\times(-2)}{3}=\frac{15}{3}=5

Hence, Solution of the given equations is,

x=-2,\:and\:y=5.

Now,

As it satisfies y=mx+3 ,

\Rightarrow 5=m(-2)+3

\Rightarrow 2m=3-5

\Rightarrow 2m=-2

\Rightarrow m=-1

Hence Value of m is -1.

Q3 Form the pair of linear equations for the following problem and find their solution by substitution method.

(i) The difference between the two numbers is 26 and one number is three times the other. Find them.

Answer:

Let two numbers be x and y and let the bigger number is y.

Now, According to the question,

y-x=26......(1)

And

y=3x......(2)

Now, the substituting value of y from (2) in (1) we get,

3x-x=26

\Rightarrow 2x=26

\Rightarrow x=13

Substituting this in (2)

\Rightarrow y=3x=3(13)=39

Hence the two numbers are 13 and 39.

Q3 Form the pair of linear equations for the following problem and find their solution by substitution method (ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.

Answer:

Let the larger angle be x and smaller angle be y

Now, As we know the sum of supplementary angles is 180. so,

x+y=180.......(1)

Also given in the question,

x-y=18.......(2)

Now, From (2) we have,

y=x-18.......(3)

Substituting this value in (1)

x+x-18=180

\Rightarrow 2x=180+18

\Rightarrow 2x=198

\Rightarrow x=99

Now, Substituting this value of x in (3), we get

\Rightarrow y=x-18=99-18=81

Hence the two supplementary angles are

99^0\:and\:81^0.

Q3 Form the pair of linear equations for the following problems and find their solution by substitution method. (iii) The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, she buys 3 bats and 5 balls for Rs 1750. Find the cost of each bat and each ball.

Answer:

Let the cost of 1 bat is x and the cost of 1 ball is y.

Now, According to the question,

7x+6y=3800......(1)

3x+5y=1750......(2)

Now, From (1) we have

y=\frac{3800-7x}{6}........(3)

Substituting this value of y in (2)

3x+5\left ( \frac{3800-7x}{6} \right )=1750

\Rightarrow 18x+19000-35x=1750\times6

\Rightarrow -17x=10500-19000

\Rightarrow -17x=-8500

\Rightarrow x=\frac{8500}{17}

\Rightarrow x=500

Now, Substituting this value of x in (3)

y=\frac{3800-7x}{6}=\frac{3800-7\times500}{6}=\frac{3800-3500}{6}=\frac{300}{6}=50

Hence, The cost of one bat is 500 Rs and the cost of one ball 50 Rs.

Q3 Form the pair of linear equations for the following problems and find their solution by substitution method. (iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs 105 and for a journey of 15 km, the charge paid is Rs 155. What are the fixed charges and the charge per km? How much does a person have to pay for traveling a distance of 25 km?

Answer:

Let the fixed charge is x and the per km charge is y.

Now According to the question

x+10y=105.......(1)

And

x+15y=155.......(2)

Now, From (1) we have,

x=105-10y........(3)

Substituting this value of x in (2), we have

105-10y+15y=155

\Rightarrow 5y=155-105

\Rightarrow 5y=50

\Rightarrow y=10

Now, Substituting this value in (3)

x=105-10y=105-10(10)=105-100=5

Hence, the fixed charge is 5 Rs and the per km charge is 10 Rs.

Now, Fair For 25 km :

\Rightarrow x+25y=5+25(10)=5+250=255

Hence fair for 25km is 255 Rs.

Q3 Form the pair of linear equations for the following problems and find their solution by substitution method. (v) A fraction becomes \frac{9}{11 }, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes \frac{5 }{6} . Find the fraction.

Answer:

Let the numerator of the fraction be x and denominator of the fraction is y

Now According to the question,

\frac{x+2}{y+2}=\frac{9}{11}

\Rightarrow 11(x+2)=9(y+2)

\Rightarrow 11x+22=9y+18

\Rightarrow 11x-9y=-4...........(1)

Also,

\frac{x+3}{y+3}=\frac{5}{6}

\Rightarrow 6(x+3)=5(y+3)

\Rightarrow 6x+18=5y+15

\Rightarrow 6x-5y=-3...........(2)

Now, From (1) we have

y=\frac{11x+4}{9}.............(3)

Substituting this value of y in (2)

6x-5\left ( \frac{11x+4}{9} \right )=-3

\Rightarrow 54x-55x-20=-27

\Rightarrow -x=20-27

\Rightarrow x=7

Substituting this value of x in (3)

y=\frac{11x+4}{9}=\frac{11(7)+4}{9}=\frac{81}{9}=9

Hence the required fraction is

\frac{x}{y}=\frac{7}{9}.

Q3 Form the pair of linear equations for the following problems and find their solution by substitution method. (vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?

Answer:

Let x be the age of Jacob and y be the age of Jacob's son,

Now, According to the question

x+5=3(y+5)

\Rightarrow x+5=3y+15

\Rightarrow x-3y=10..........(1)

Also,

x-5=7(y-5)

\Rightarrow x-5=7y-35

\Rightarrow x-7y=-30.........(2)

Now,

From (1) we have,

x=10+3y...........(3)

Substituting this value of x in (2)

10+3y-7y=-30

\Rightarrow -4y=-30-10

\Rightarrow 4y=40

\Rightarrow y=10

Substituting this value of y in (3),

x=10+3y=10+3(10)=10+30=40

Hence, Present age of Jacob is 40 years and the present age of Jacob's son is 10 years.

Pair of linear equations in two variables class 10 solutions Excercise: 3.4

Q1 Solve the following pair of linear equations by the elimination method and the substitution method :

(i) x + y =5 \ \textup{and} \ 2x - 3y = 4

Answer:

Elimination Method:

Given, equations

\\x + y =5............(1) \ \textup{and} \\ \ 2x - 3y = 4........(2)

Now, multiplying (1) by 3 we, get

\\3x +3 y =15............(3)

Now, Adding (2) and (3), we get

\\2x-3y+3x +3 y =4+15

\Rightarrow 5x=19

\Rightarrow x=\frac{19}{5}

Substituting this value in (1) we, get

\frac{19}{5}+y=5

\Rightarrow y=5-\frac{19}{5}

\Rightarrow y=\frac{6}{5}

Hence,

x=\frac{19}{5}\:and\:y=\frac{6}{5}

Substitution method :

Given, equations

\\x + y =5............(1) \ \textup{and} \\ \ 2x - 3y = 4........(2)

Now, from (1) we have,

y=5-x.......(3)

substituting this value in (2)

2x-3(5-x)=4

\Rightarrow 2x-15+3x=4

\Rightarrow 5x=19

\Rightarrow x=\frac{19}{5}

Substituting this value of x in (3)

\Rightarrow y=5-x=5-\frac{19}{5}=\frac{6}{5}

Hence,

x=\frac{19}{5}\:and\:y=\frac{6}{5}

Q1 Solve the following pair of linear equations by the elimination method and the substitution method :

(ii) 3x + 4 y = 10 \ \textup{and} \ 2x - 2y = 2

Answer:

Elimination Method:

Given, equations

\\3x + 4 y = 10............(1) \ \textup{and}\\ \ 2x - 2y = 2..............(2)

Now, multiplying (2) by 2 we, get

\\4x -4 y =4............(3)

Now, Adding (1) and (3), we get

\\3x+4y+4x -4 y =10+4

\Rightarrow 7x=14

\Rightarrow x=2

Putting this value in (2) we, get

2(2)-2y=2

\Rightarrow 2y=2

\Rightarrow y=1

Hence,

x=2\:and\:y=1

Substitution method :

Given, equations

\\3x + 4 y = 10............(1) \ \textup{and}\\ \ 2x - 2y = 2..............(2)

Now, from (2) we have,

y=\frac{2x-2}{2}=x-1.......(3)

substituting this value in (1)

3x+4(x-1)=10

\Rightarrow 3x+4x-4=10

\Rightarrow 7x=14

\Rightarrow x=2

Substituting this value of x in (3)

\Rightarrow y=x-1=2-1=1

Hence,

x=2\:and\:y=1

Q1 Solve the following pair of linear equations by the elimination method and the substitution method: (iii) 3x - 5y -4 = 0\ \textup{and} \ 9x = 2y + 7

Answer:

Elimination Method:

Given, equations

\\3x - 5y -4 = 0..........(1)\ \textup{and}\ \\9x = 2y + 7

\\\Rightarrow 9x - 2y -7=0........(2)

Now, multiplying (1) by 3 we, get

\\9x -15 y -12=0............(3)

Now, Subtracting (3) from (2), we get

9x-2y-7-9x+15y+12=0

\Rightarrow 13y+5=0

\Rightarrow y=\frac{-5}{13}

Putting this value in (1) we, get

3x-5(\frac{-5}{13})-4=0

\Rightarrow 3x=4-\frac{25}{13}

\Rightarrow 3x=\frac{27}{13}

\Rightarrow x=\frac{9}{13}

Hence,

x=\frac{9}{13}\:and\:y=-\frac{5}{13}

Substitution method :

Given, equations

\\3x - 5y -4 = 0..........(1)\ \textup{and}\ \\9x = 2y + 7

\\\Rightarrow 9x - 2y -7=0........(2)

Now, from (2) we have,

y=\frac{9x-7}{2}.......(3)

substituting this value in (1)

3x-5\left(\frac{9x-7}{2} \right )-4=0

\Rightarrow 6x-45x+35-8=0

\Rightarrow -39x+27=0

\Rightarrow x=\frac{27}{39}=\frac{9}{13}

Substituting this value of x in (3)

\Rightarrow y=\frac{9(9/13)-7}{2}=\frac{81/13-7}{2}=\frac{-5}{13}

Hence,

x=\frac{9}{13}\:and\:y=-\frac{5}{13}

Q1 Solve the following pair of linear equations by the elimination method and the substitution method :(iv) \frac{x}{2} + \frac{2y}{3} = -1\ \textup{and} \ x - \frac{y}{3} = 3

Answer:

Elimination Method:

Given, equations

\\\frac{x}{2} + \frac{2y}{3} = -1........(1)\ \textup{and} \ \\ \\x - \frac{y}{3} = 3............(2)

Now, multiplying (2) by 2 we, get

\\2x - \frac{2y}{3} =6............(3)

Now, Adding (1) and (3), we get

\\\frac{x}{2}+\frac{2y}{3}+2x-\frac{2y}{3}=-1+6

\Rightarrow \frac{5x}{2}=5

\Rightarrow x=2

Putting this value in (2) we, get

2-\frac{y}{3}=3

\Rightarrow \frac{y}{3}=-1

\Rightarrow y=-3

Hence,

x=2\:and\:y=-3

Substitution method :

Given, equations

\\\frac{x}{2} + \frac{2y}{3} = -1........(1)\ \textup{and} \ \\ \\x - \frac{y}{3} = 3............(2)

Now, from (2) we have,

y=3(x-3)......(3)

substituting this value in (1)

\frac{x}{2}+\frac{2(3(x-3))}{3}=-1

\Rightarrow \frac{x}{2}+2x-6=-1

\Rightarrow \frac{5x}{2}=5

\Rightarrow x=2

Substituting this value of x in (3)

\Rightarrow y=3(x-3)=3(2-1)=-3

Hence,

x=2\:and\:y=-3

Q2 Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : (i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes \frac{1}{2 } if we only add 1 to the denominator. What is the fraction?

Answer:

Let the numerator of the fraction be x and denominator is y,

Now, According to the question,

\frac{x+1}{y-1}=1

\Rightarrow x+1=y-1

\Rightarrow x-y=-2.........(1)

Also,

\frac{x}{y+1}=\frac{1}{2}

\Rightarrow 2x=y+1

\Rightarrow 2x-y=1..........(2)

Now, Subtracting (1) from (2) we get

x=3

Putting this value in (1)

3-y=-2

\Rightarrow y=5

Hence

x=3\:and\:y=5

And the fraction is

\frac{3}{5}

Q2 Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : (ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?

Answer:

Let the age of Nuri be x and age of Sonu be y.

Now, According to the question

x-5=3(y-5)

\Rightarrow x-5=3y-15

\Rightarrow x-3y=-10.........(1)

Also,

x+10=2 (y+10)

\Rightarrow x+10=2y+20

\Rightarrow x-2y=10........(2)

Now, Subtracting (1) from (2), we get

y=20

putting this value in (2)

x-2(20)=10

\Rightarrow x=50

Hence the age of Nuri is 50 and the age of Nuri is 20.

Q2 Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.

Answer:

Let the unit digit of the number be x and 10's digit be y.

Now, According to the question,

x+y=9.......(1) 24323

Also

9(10y+x)=2(10x+y)

\Rightarrow 90y+9x=20x+2y

\Rightarrow 88y-11x=0

\Rightarrow 8y-x=0.........(2)

Now adding (1) and (2) we get,

\Rightarrow 9y=9

\Rightarrow y=1

now putting this value in (1)

x+1=9

\Rightarrow x=8

Hence the number is 18.

Q2 Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (iv) Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes of Rs 50 and Rs 100 she received.

Answer:

Let the number of Rs 50 notes be x and the number of Rs 100 notes be y.

Now, According to the question,

x+y=25..........(1)

And

50x+100y=2000

\Rightarrow x+2y=40.............(2)

Now, Subtracting(1) from (2), we get

y=15

Putting this value in (1).

x+15=25

\Rightarrow x=10

Hence Meena received 10 50 Rs notes and 15 100 Rs notes.

Q2 Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.

Answer:

Let fixed charge be x and per day charge is y.

Now, According to the question,

x+4y=27...........(1)

And

x+2y=21...........(2)

Now, Subtracting (2) from (1). we get,

4y-2y=27-21

\Rightarrow 2y=6

\Rightarrow y=3

Putting this in (1)

x+4(3)=27

\Rightarrow x=27-12=15

Hence the fixed charge is 15 Rs and per day charge is 3 Rs.

Pair of linear equations in two variables class 10 solutions Excercise: 3.5

Q1 Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions? In case there is a unique solution, find it by using a cross multiplication method.

(i) \\x - 3y -3 = 0\\ 3x - 9y -2 = 0

Answer:

Given, two equations,

\\x - 3y -3 = 0.........(1)\\ 3x - 9y -2 = 0........(2)

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{1}{3}

\frac{b_1}{b_2}=\frac{-3}{-9}=\frac{1}{3}

\frac{c_1}{c_2}=\frac{-3}{-2}=\frac{3}{2}

As we can see,

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

Hence, the pair of equations has no solution.

Q1 Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions? In case there is a unique solution, find it by using a cross multiplication method.

(ii) \\2x + y = 5 \\ 3x + 2y = 8

Answer:

Given, two equations,

\\2x + y = 5.........(1) \\ 3x + 2y = 8..........(2)

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{2}{3}

\frac{b_1}{b_2}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{5}{8}

As we can see,

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

Hence, the pair of equations has exactly one solution.

By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(1)(-8)-(2)(-5)}=\frac{y}{(-5)(3)-(-8)(2)}=\frac{1}{(2)(2)-(3)(1)}

\frac{x}{2}=\frac{y}{1}=\frac{1}{1}

x=2,\:and\:y=1

Q1 Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions? In case there is a unique solution, find it by using a cross multiplication method.

(iii) \\3x -5 y = 20\\ 6x - 10y = 40

Answer:

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{-5}{-10}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{20}{40}=\frac{1}{2}

As we can see,

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

Hence, the pair of equations has infinitely many solutions.

Q1 Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions? In case there is a unique solution, find it by using a cross multiplication method.

(iv) \\x - 3y -7 = 0\\ 3x -3y -15 =0

Answer:

Given the equations,

\\x - 3y -7 = 0.........(1)\\ 3x -3y -15 =0........(2)

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{1}{3}

\frac{b_1}{b_2}=\frac{-3}{-3}=1

\frac{c_1}{c_2}=\frac{-7}{-15}=\frac{7}{15}

As we can see,

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

Hence, the pair of equations has exactly one solution.

By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(-3)(-15)-(-3)(-7)}=\frac{y}{(-7)(3)-(-15)(1)}=\frac{1}{(1)(-3)-(3)(-3)}

\frac{x}{45-21}=\frac{y}{-21+15}=\frac{1}{-3+9}

\frac{x}{24}=\frac{y}{-6}=\frac{1}{6}

x=\frac{24}{6}=4,\:and\:y=-1

Q2 (i) For which values of a and b does the following pair of linear equations have an infinite number of solutions? \\2x + 3y = 7 \\(a - b) x + (a + b) y = 3a + b - 2

Answer:

Given equations,

\\2x + 3y = 7 \\(a - b) x + (a + b) y = 3a + b - 2

As we know, the condition for equations a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 to have an infinite solution is

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

So, Comparing these equations with, a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{2}{a-b}=\frac{3}{a+b}=\frac{7}{3a+b-2}

From here we get,

\frac{2}{a-b}=\frac{3}{a+b}

\Rightarrow 2(a+b)=3(a-b)

\Rightarrow 2a+2b=3a-3b

\Rightarrow a-5b=0.........(1)

Also,

\frac{2}{a-b}=\frac{7}{3a+b-2}

\Rightarrow 2(3a+b-2)=7(a-b)

\Rightarrow 6a+2b-4=7a-7b

\Rightarrow a-9b+4=0...........(2)

Now, Subtracting (2) from (1) we get

\Rightarrow 4b-4=0

\Rightarrow b=1

Substituting this value in (1)

\Rightarrow a-5(1)=0

\Rightarrow a=5

Hence, a=5\:and\:b=1 .

Q2 (ii) For which value of k will the following pair of linear equations have no solution? \\3x + y = 1 \\(2k - 1) x + (k - 1) y = 2k + 1

Answer:

Given, the equations,

\\3x + y = 1 \\(2k - 1) x + (k - 1) y = 2k + 1

As we know, the condition for equations a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 to have no solution is

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

So, Comparing these equations with, a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{3}{2k-1}=\frac{1}{k-1}\neq\frac{1}{2k+1}

From here we get,

\frac{3}{2k-1}=\frac{1}{k-1}

\Rightarrow 3(k-1)=2k-1

\Rightarrow 3k-3=2k-1

\Rightarrow 3k-2k=3-1

\Rightarrow k=2

Hence, the value of K is 2.

Q3 Solve the following pair of linear equations by the substitution and cross-multiplication methods :
\\8x + 5y = 9 \\3x + 2y = 4

Answer:

Given the equations

\\8x + 5y = 9........(1) \\3x + 2y = 4........(2)

By Substitution Method,

From (1) we have

y=\frac{9-8x}{5}.........(3)

Substituting this in (2),

3x+2\left ( \frac{9-8x}{5} \right )=4

\Rightarrow 15x+18-16x=20

\Rightarrow -x=20-18

\Rightarrow x=-2

Substituting this in (3)

y=\frac{9-8x}{5}=\frac{9-8(-2)}{5}=\frac{25}{5}=5

Hence x=-2\:and\:y=5 .

By Cross Multiplication Method

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(5)(-4)-(2)(-9)}=\frac{y}{(3)(-9)-(8)(-4)}=\frac{1}{(8)(2)-(3)(5)}

\frac{x}{-20+18}=\frac{y}{32-27}=\frac{1}{16-15}

\frac{x}{-2}=\frac{y}{5}=\frac{1}{1}

x=-2,\:and\:y=5

Q4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.

Answer:

Let the fixed charge be x and the cost of food per day is y,

Now, According to the question

x+20y=1000.........(1)

Also

x+26y=1180.........(2)

Now subtracting (1) from (2),

x+26y-x-20y=1180-100

\Rightarrow 6y=180

\Rightarrow y=30

Putting this value in (1)

x+20(30)=1000

\Rightarrow x=1000-600

\Rightarrow x=400

Hence, the Fixed charge is Rs 400 and the cost of food per day is Rs 30.

Q4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (ii) A fraction becomes \frac{1}{3}when 1 is subtracted from the numerator and it becomes \frac{1}{4} when 8 is added to its denominator. Find the fraction.

Answer:

Let numerator of a fraction be x and the denominator is y.

Now, According to the question,

\frac{x-1}{y}=\frac{1}{3}

\Rightarrow 3(x-1)=y

\Rightarrow 3x-3=y

\Rightarrow 3x-y=3........(1)

Also,

\frac{x}{y+8}=\frac{1}{4}

\Rightarrow 4x=y+8

\Rightarrow 4x-y=8.........(2)

Now, Subtracting (1) from (2) we get,

4x-3x=8-3

\Rightarrow x=5

Putting this value in (2) we get,

4(5)-y=8

\Rightarrow y=20-8

\Rightarrow y=12

Hence, the fraction is

\frac{x}{y}=\frac{5}{12} .

Q4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?

Answer:

Let the number of right answer and wrong answer be x and y respectively

Now, According to the question,

3x-y=40..........(1)

And

\\4x-2y=50\\\Rightarrow 2x-y=25..........(2)

Now, subtracting (2) from (1) we get,

x=40-25

x=15

Putting this value in (1)

3(15)-y=40

\Rightarrow y=45-40

\Rightarrow y=5

Hence the total number of question is x+y=15+5=20.

Q4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?

Answer:

Let the speed of the first car is x and the speed of the second car is y.

Let's solve this problem by using relative motion concept,

the relative speed when they are going in the same direction= x - y

the relative speed when they are going in the opposite direction= x + y

The given relative distance between them = 100 km.

Now, As we know,

Relative distance = Relative speed * time .

So, According to the question,

5\times(x-y)=100

\Rightarrow 5x-5y=100

\Rightarrow x-y=20.........(1)

Also,

1(x+y)=100

\Rightarrow x+y=100........(2)

Now Adding (1) and (2) we get

2x=120

\Rightarrow x=60

putting this in (1)

60-y=20

\Rightarrow y=60-20

\Rightarrow y=40

Hence the speeds of the cars are 40 km/hour and 60 km/hour.

Q4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (v) The area of a rectangle gets reduced by 9 square units if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

Answer:

Let lbe the length of the rectangle and b be the width,

Now, According to the question,

(l-5)(b+3)=lb-9

\Rightarrow lb+3l-5b-15=lb-9

\Rightarrow 3l-5b-6=0..........(1)

Also,

(l+3)(b+2)=lb+67

\Rightarrow lb+2l+3b+6=lb+67

\Rightarrow 2l+3b-61=0..........(2)

By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(-5)(-61)-(3)(-6)}=\frac{y}{(-6)(2)-(-61)(3)}=\frac{1}{(3)(3)-(2)(-5)}

\frac{x}{305+18}=\frac{y}{-12+183}=\frac{1}{9+10}

\frac{x}{323}=\frac{y}{171}=\frac{1}{19}

x=17,\:and\:y=9

Hence the length and width of the rectangle are 17 units and 9 units respectively.

NCERT Solutions for class 10 math chapter 3 Pair of Linear Equations in Two Variables Excercise: 3.6

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(i) \\\frac{1}{2x} +\frac{1}{3y} = 2\\ \frac{1}{3x} + \frac{1}{2y} = \frac{13}{6}

Answer:

Given Equations,

\\\frac{1}{2x} +\frac{1}{3y} = 2\\ \frac{1}{3x} + \frac{1}{2y} = \frac{13}{6}

Let,

\frac{1}{x}=p\:and\:\frac{1}{y}=q

Now, our equation becomes

\frac{p}{2}+\frac{q}{3}=2

\Rightarrow 3p+2q=12........(1)

And

\frac{p}{3}+\frac{q}{2}=\frac{13}{6}

\Rightarrow 2p+3q=13..........(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{p}{(2)(-13)-(3)(-12)}=\frac{q}{(-12)(2)-(-13)(3)}=\frac{1}{(3)(3)-(2)(2)}

\frac{p}{-26+36}=\frac{q}{-24+39}=\frac{1}{9-4}

\frac{p}{10}=\frac{q}{15}=\frac{1}{5}

p=2,\:and\:q=3

And Hence,

x=\frac{1}{2}\:and\:y=\frac{1}{3}.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(ii) \\ \frac{2}{\sqrt x} + \frac{3}{\sqrt y} = 2\\ \frac{4}{\sqrt x} - \frac{9}{\sqrt y} = -1

Answer:

Given Equations,

\\ \frac{2}{\sqrt x} + \frac{3}{\sqrt y} = 2\\ \frac{4}{\sqrt x} - \frac{9}{\sqrt y} = -1

Let,

\frac{1}{\sqrt{x}}=p\:and\:\frac{1}{\sqrt{y}}=q

Now, our equation becomes

2p+3q=2........(1)

And

4p-9q=-1..........(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{p}{(3)(1)-(-9)(-2)}=\frac{q}{(-2)(4)-(1)(2)}=\frac{1}{(2)(-9)-(4)(3)}

\frac{p}{3-18}=\frac{q}{-8-2}=\frac{1}{-18-12}

\frac{p}{-15}=\frac{q}{-10}=\frac{1}{-30}

p=\frac{1}{2},\:and\:q=\frac{1}{3}

So,

p=\frac{1}{2}=\frac{1}{\sqrt{x}}\Rightarrow x=4

q=\frac{1}{3}=\frac{1}{\sqrt{y}}\Rightarrow y=9 .

And hence

x=4\:and\:y=9.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(iii) \\\frac{4}{x} + 3y = 14\\ \frac{3}{x} - 4y = 23

Answer:

Given Equations,

\\\frac{4}{x} + 3y = 14\\ \frac{3}{x} - 4y = 23

Let,

\frac{1}{x}=p\:and\:y=q

Now, our equation becomes

\Rightarrow 4p+3q=14........(1)

And

\Rightarrow 3p-4q=23..........(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{p}{(3)(-23)-(-4)(-14)}=\frac{q}{(-14)(3)-(-23)(4)}=\frac{1}{(4)(-4)-(3)(3)}

\frac{p}{-69-56}=\frac{q}{-42+92}=\frac{1}{-16-9}

\frac{p}{-125}=\frac{q}{50}=-\frac{1}{25}

p=5,\:and\:q=-2

And Hence,

x=\frac{1}{5}\:and\:y=-2.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(iv) \\\frac{5}{x - 1} + \frac{1}{y -2} = 2\\ \frac{6}{x-1} - \frac{3}{y -2} =1

Answer:

Given Equations,

\\\frac{5}{x - 1} + \frac{1}{y -2} = 2\\ \frac{6}{x-1} - \frac{3}{y -2} =1

Let,

\frac{1}{x-1}=p\:and\:\frac{1}{y-2}=q

Now, our equation becomes

5p+q=2........(1)

And

6p-3q=1..........(2)

Multiplying (1) by 3 we get

15p+3q=6..........(3)

Now, adding (2) and (3) we get

21p=7

\Rightarrow p=\frac{1}{3}

Putting this in (2)

6\left ( \frac{1}{3} \right )-3q=1

\Rightarrow 3q=1

\Rightarrow q=\frac{1}{3}

Now,

p=\frac{1}{3}=\frac{1}{x-1}\Rightarrow x-1=3\Rightarrow x=4

q=\frac{1}{3}=\frac{1}{y-2}\Rightarrow y-2=3\Rightarrow x=5

Hence,

x=4,\:and\:y=5.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations: (v)

\\\frac{7x - 2y}{xy} = 5\\ \frac{8x + 7y}{xy} = 15

Answer:

Given Equations,

\\\frac{7x - 2y}{xy} = 5\\\\\Rightarrow\frac{7}{y} -\frac{2}{x}=5\\ \frac{8x + 7y}{xy} = 15\\\Rightarrow \frac{8}{y}+\frac{7}{x}=15

Let,

\frac{1}{x}=p\:and\:\frac{1}{y}=q

Now, our equation becomes

7q-2p=5........(1)

And

8q+7p=15..........(2)

By Cross Multiplication method,

\frac{q}{b_1c_2-b_2c_1}=\frac{p}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{q}{(-2)(-15)-(7)(-5)}=\frac{p}{(-5)(8)-(-15)(7)}=\frac{1}{(7)(7)-(8)(-2)}

\frac{q}{30+35}=\frac{p}{-40+105}=\frac{1}{49 +16}

\frac{q}{65}=\frac{p}{65}=\frac{1}{65}

p=1,\:and\:q=1

And Hence,

x=1\:and\:y=1.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(vi) \\6x + 3y = 6xy\\ 2x + 4y = 5 xy

Answer:

Given Equations,

\\6x + 3y = 6xy\\\Rightarrow \frac{6x}{xy}+\frac{3y}{xy}=6\\\\\Rightarrow \frac{6}{y}+\frac{3}{x}=6\\and\\\ 2x + 4y = 5 xy\\\Rightarrow \frac{2x}{xy}+\frac{4y}{xy}=5\\\Rightarrow \frac{2}{y}+\frac{4}{x}=5

Let,

\frac{1}{x}=p\:and\:\frac{1}{y}=q

Now, our equation becomes

6q+3p=6........(1)

And

2q+4p=5..........(2)

By Cross Multiplication method,

\frac{q}{b_1c_2-b_2c_1}=\frac{p}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{q}{(3)(-5)-(-6)(4)}=\frac{p}{(6)(2)-(6)(-5)}=\frac{1}{(6)(4)-(3)(2)}

\frac{q}{-15+24}=\frac{p}{-12+30}=\frac{1}{24 -6}

\frac{q}{9}=\frac{p}{18}=\frac{1}{18}

q=\frac{1}{2}\:and\:p=1

And Hence,

x=1\:and\:y=2.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:
(vii) \\\frac{10}{x + y} + \frac{2}{x - y}= 4\\ \frac{15}{x+y} - \frac{5}{x - y} = -2


Answer:

Given Equations,

\\\frac{10}{x + y} + \frac{2}{x - y}= 4\\ \frac{15}{x+y} - \frac{5}{x - y} = -2

Let,

\frac{1}{x+y}=p\:and\:\frac{1}{x-y}=q

Now, our equation becomes

10p+2q=4........(1)

And

15p-5q=-2..........(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{p}{(2)(2)-(-5)(-4)}=\frac{q}{(-4)(15)-(2)(10)}=\frac{1}{(10)(-5)-(15)(2)}

\frac{p}{4-20}=\frac{q}{-60-20}=\frac{1}{-50-30}

\frac{p}{-16}=\frac{q}{-80}=\frac{1}{-80}

p=\frac{1}{5},\:and\:q=1

Now,

p=\frac{1}{5}=\frac{1}{x+y}

\Rightarrow x+y=5........(3)

And,

q=1=\frac{1}{x-y}

\Rightarrow x-y=1...........(4)

Adding (3) and (4) we get,

\Rightarrow 2x=6

\Rightarrow x=3

Putting this value in (3) we get,

3+y=5

\Rightarrow y=2

And Hence,

x=3\:and\:y=2.

Q1 Solve the following pairs of equations by reducing them to a pair of linear equations:

(viii) \\\frac{1}{3x + y} + \frac{1}{3x -y} = \frac{3}{4}\\ \frac{1}{2(3x+y)} - \frac{1}{2(3x -y)} = \frac{-1}{8}


Answer:

Given Equations,

\\\frac{1}{3x + y} + \frac{1}{3x -y} = \frac{3}{4}\\ \frac{1}{2(3x+y)} - \frac{1}{2(3x -y)} = \frac{-1}{8}

Let,

\frac{1}{3x+y}=p\:and\:\frac{1}{3x-y}=q

Now, our equation becomes

p+q=\frac{3}{4}.........(1)

And

\\\frac{p}{2}-\frac{q}{2}=\frac{-1}{8}\\\\p-q=\frac{-1}{4}..........(2)

Now, Adding (1) and (2), we get

2p=\frac{3}{4}-\frac{1}{4}

\Rightarrow 2p=\frac{2}{4}

\Rightarrow p=\frac{1}{4}

Putting this value in (1)

\frac{1}{4}+q=\frac{3}{4}

\Rightarrow q=\frac{3}{4}-\frac{1}{4}

\Rightarrow q=\frac{2}{4}

\Rightarrow q=\frac{1}{2}

Now,

p=\frac{1}{4}=\frac{1}{3x+y}

\Rightarrow 3x+y=4...........(3)

And

q=\frac{1}{2}=\frac{1}{3x-y}

\Rightarrow 3x-y=2............(4)

Now, Adding (3) and (4), we get

6x=4+2

\Rightarrow 6x=6

\Rightarrow x=1

Putting this value in (3),

3(1)+y=4

\Rightarrow y=4-3

\Rightarrow y=1

Hence,

x=1,\:and\:y=1

Q2 Formulate the following problems as a pair of equations and hence find their solutions: (i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.

Answer:

Let the speed of Ritu in still water be x and speed of current be y,

Let's solve this problem by using relative motion concept,

the relative speed when they are going in the same direction (downstream)= x +y

the relative speed when they are going in the opposite direction (upstream)= x - y

Now, As we know,

Relative distance = Relative speed * time .

So, According to the question,

x+y=\frac{20}{2}

\Rightarrow x+y=10.........(1)

And,

x-y=\frac{4}{2}

\Rightarrow x-y=2...........(2)

Now, Adding (1) and (2), we get

2x=10+2

\Rightarrow 2x=12

\Rightarrow x=6

Putting this in (2)

6-y=2

\Rightarrow y=6-2

\Rightarrow y=4

Hence,

x=6\:and\:y=4.

Hence Speed of Ritu in still water is 6 km/hour and speed of the current is 4 km/hour

Q2 Formulate the following problems as a pair of equations and hence find their solutions: (ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.

Answer:

Let the number of days taken by woman and man be x and y respectively,

The proportion of Work done by a woman in a single day

=\frac{1}{x }

The proportion of Work done by a man in a single day

=\frac{1}{y }

Now, According to the question,

4\left ( \frac{2}{x}+\frac{5}{y} \right )=1

\Rightarrow \left ( \frac{2}{x}+\frac{5}{y} \right )=\frac{1}{4}

Also,

3\left ( \frac{3}{x}+\frac{6}{y} \right )=1

\Rightarrow \left ( \frac{3}{x}+\frac{6}{y} \right )=\frac{1}{3}

Let,

\frac{1}{x}=p\:and\:\frac{1}{y}=q

Now, our equation becomes

2p+5q=\frac{1}{4}

8p+20q=1........(1)

And

3p+6p=\frac{1}{3}

\Rightarrow 9p+18p=1.............(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{p}{(20)(-1)-(18)(-1)}=\frac{q}{(-1)(9)-(8)(-1)}=\frac{1}{(8)(18)-(20)(9)}

\frac{p}{-20+18}=\frac{q}{-9+8}=\frac{1}{146 -60}

\frac{p}{-2}=\frac{q}{-1}=\frac{1}{-36}

p=\frac{1}{18},\:and\:q=\frac{1}{36}

So,

x=18\:and\:y=36.

Q2 Formulate the following problems as a pair of equations and hence find their solutions: (iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Answer:

Let the speed of the train and bus be u and v respectively

Now According to the question,

\frac{60}{u}+\frac{240}{v}=4

And

\frac{100}{u}+\frac{200}{v}=4+\frac{1}{6}

\Rightarrow \frac{100}{u}+\frac{200}{v}=\frac{25}{6}

Let,

\frac{1}{u}=p\:and\:\frac{1}{v}=q

Now, our equation becomes

60p+140q=4

\Rightarrow 15p+60q=1.........(1)

And

100p+200q=\frac{25}{6}

\Rightarrow 4p+8q=\frac{1}{6}

\Rightarrow 24p+48q=1..........(2)

By Cross Multiplication method,

\frac{p}{b_1c_2-b_2c_1}=\frac{q}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{q}{(60)(-1)-(48)(-1)}=\frac{p}{(-1)(24)-(-1)(15)}=\frac{1}{(15)(48)-(60)(24)}

\frac{p}{-60+48}=\frac{q}{-24+15}=\frac{1}{720-1440}

\frac{p}{-12}=\frac{q}{-9}=\frac{1}{-720}

p=\frac{12}{720}=\frac{1}{60},\:and\:q=\frac{9}{720}=\frac{1}{80}

And Hence,

x=60\:and\:y=80

Hence the speed of the train and bus are 60 km/hour and 80 km/hour respectively.

Class 10 math chapter 3 solutions Pair of Linear Equations in Two Variables Excercise: 3.7

Q1 The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.

Answer:

Let the age of Ani be a, age of Biju be b ,

Case 1: when Ani is older than Biju

age of Ani's father Dharam:

d=2a and

age of his sister Cathy :

c=\frac{b}{2}

Now According to the question,

a-b=3...........(1)

Also,

\\d-c=30 \\\Rightarrow 2a-\frac{b}{2}=30

\Rightarrow 4a-b=60..............(2)

Now subtracting (1) from (2), we get,

3a=60-3

\Rightarrow a=19

putting this in (1)

19-b=3

\Rightarrow b=16

Hence the age of Ani and Biju is 19 years and 16 years respectively.

Case 2:

b-a=3..........(3)

And

\\d-c=30 \\\Rightarrow 2a-\frac{b}{2}=30

\Rightarrow 4a-b=60..............(4)

Now Adding (3) and (4), we get,

3a=63

\Rightarrow a=21

putting it in (3)

b-21=3

\Rightarrow b=24.

Hence the age of Ani and Biju is 21 years and 24 years respectively.

Q2 One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II]

[Hint : x + 100 = 2(y - 100), y + 10 = 6(x - 10) ]

Answer:

Let the amount of money the first person and the second person having is x and y respectively

Noe, According to the question.

x + 100 = 2(y - 100)

\Rightarrow x - 2y =-300...........(1)

Also

y + 10 = 6(x - 10)

\Rightarrow y - 6x =-70..........(2)

Multiplying (2) by 2 we get,

2y - 12x =-140..........(3)

Now adding (1) and (3), we get

-11x=-140-300

\Rightarrow 11x=440

\Rightarrow x=40

Putting this value in (1)

40-2y=-300

\Rightarrow 2y=340

\Rightarrow y=170

Thus two friends had 40 Rs and 170 Rs respectively.


Q3 A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.

Answer:

Let the speed of the train be v km/h and the time taken by train to travel the given distance be t hours and the distance to travel be d km.

Now As we Know,

speed=\frac{distance }{time}

\Rightarrow v=\frac{d}{t}


\Rightarrow d=vt..........(1)
Now, According to the question,
(v+10)=\frac{d}{t-2}

\Rightarrow (v+10){t-2}=d

\Rightarrow vt +10t-2v-20=d

Now, Using equation (1), we have

\Rightarrow -2v+10t=20............(2)
Also,

(v-10)=\frac{d}{t+3}

\Rightarrow (v-10)({t+3})=d

\Rightarrow vt+3v-10t-30=d
\Rightarrow3v-10t=30..........(3)

Adding equations (2) and (3), we obtain:
v=50.
Substituting the value of x in equation (2), we obtain:
(-2)(50)+10t=20

\Rightarrow -100+10t=20

\Rightarrow 10t=120

\Rightarrow t=12
Putting this value in (1) we get,

d=vt=(50)(12)=600

Hence the distance covered by train is 600km.

Q4 The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.

Answer:

Let the number of rows is x and the number of students in a row is y.
Total number of students in the class = Number of rows * Number of students in a row
=xy

Now, According to the question,

\\xy = (x - 1) (y + 3) \\\Rightarrow xy= xy - y + 3x - 3 \\\Rightarrow 3x - y - 3 = 0 \\ \Rightarrow 3x - y = 3 ...... ... (1)

Also,

\\xy=(x+2)(y-3)\\\Rightarrow xy = xy + 2y - 3x - 6 \\ \Rightarrow 3x - 2y = -6 ... (2)
Subtracting equation (2) from (1), we get:
y=9
Substituting the value of y in equation (1), we obtain:
\\3x - 9 = 3 \\\Rightarrow 3x = 9 + 3 = 12 \\\Rightarrow x = 4
Hence,
The number of rows is 4 and the Number of students in a row is 9.

Total number of students in a class

: xy=(4)(9)=36

Hence there are 36 students in the class.

Q5 In a \Delta\textup{ABC}, \angle C = 3 \angle B = 2( \angle A + \angle B) . Find the three angles.

Answer:

Given,

\angle C = 3 \angle B = 2(\anlge A + \angle B)

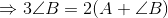
\Rightarrow 3 \angle B = 2(\anlge A + \angle B)

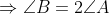
\Rightarrow \angle B = 2 \angle A

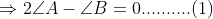
\Rightarrow 2 \angle A -\angle B = 0..........(1)

Also, As we know that the sum of angles of a triangle is 180, so

\angle A +\angle B+ \angle C=180

\angle A +\angle B+ 3\angle B=180^0

\angle A + 4\angle B=180^0..........(2)

Now From (1) we have

\angle B = 2 \angle A.......(3)

Putting this value in (2) we have

\angle A + 4(2\angle A)=180^0.

\Rightarrow 9\angle A=180^0.

\Rightarrow \angle A=20^0.

Putting this in (3)

\angle B = 2 (20)=40^0

And

\angle C = 3 \angle B =3(40)=120^0

Hence three angles of triangles 20^0,40^0\:and\:120^0.

Q6 Draw the graphs of the equations 5x - y =5and 3x - 7 = 3 . Determine the coordinates of the vertices of the triangle formed by these lines and the y-axis.

Answer:

Given two equations,

5x - y =5.........(1)

And

3x - y = 3........(2)

Points(x,y) which satisfies equation (1) are:

X
0
1
5
Y
-5
0
20

Points(x,y) which satisfies equation (1) are:

X
0
1
2
Y
-3
0
3


GRAPH:

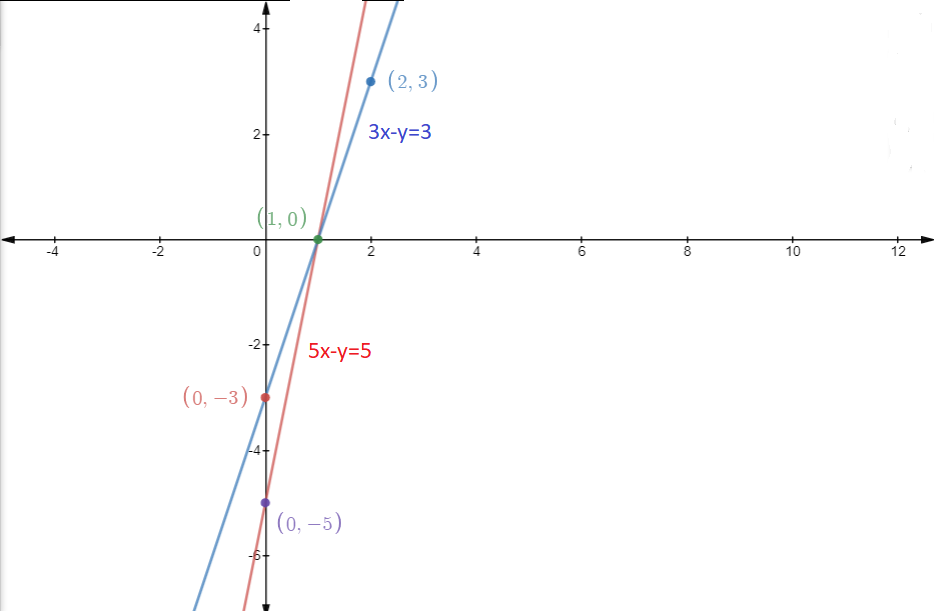
Graph

As we can see from the graph, the three points of the triangle are, (0,-3),(0,-5) and (1,0).

Q7 Solve the following pair of linear equations: (i) \\px + qy = p - q\\ qx - py = p + q

Answer:

Given Equations,

\\px + qy = p - q.........(1)\\ qx - py = p + q.........(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(q)(-p-q)-(q-p)(-p)}=\frac{y}{(q-p)(q)-(p)(-p-q)}=\frac{1}{(p)(-p)-(q)(q)}

\frac{x}{-p^2-q^2}=\frac{y}{p^2+q^2}=\frac{1}{-p^2-q^2}

x=1,\:and\:y=-1

Q7 Solve the following pair of linear equations: (ii) \\ax + by = c\\ bx +ay = 1 + c

Answer:

Given two equations,

\\ax + by = c.........(1)\\ bx +ay = 1 + c.........(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(b)(-1-c)-(-c)(a)}=\frac{y}{(-c)(b)-(a)(-1-c)}=\frac{1}{(a)(a)-(b)(b)}

\frac{x}{-b-bc+ac}=\frac{y}{-cb+a+ac}=\frac{1}{a^2-b^2}

x=\frac{-b-bc+ac}{a^2-b^2},\:and\:y=\frac{a-bc+ac}{a^2-b^2}


Q7 Solve the following pair of linear equations: (iii) \\\frac{x}{a} - \frac{y}{b} = 0\\ ax + by = a^2 +b^2

Answer:

Given equation,

\\\frac{x}{a} - \frac{y}{b} = 0\\\Rightarrow bx-ay=0...........(1)\\ ax + by = a^2 +b^2...............(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(-a)(-a^2-b^2)-(b)(0)}=\frac{y}{(0)(a)-(b)(-a^2-b^2)}=\frac{1}{(b)(b)-(-a)(a)}

\frac{x}{a(a^2+b^2)}=\frac{y}{b(a^2+b^2)}=\frac{1}{a^2+b^2}

x=a,\:and\:y=b

Q7 Solve the following pair of linear equations: (iv) \\(a-b)x + (a+b)y = a^2 -2ab - b^2\\ (a+b)(x+y) = a^2 +b^2

Answer:

Given,

\\(a-b)x + (a+b)y = a^2 -2ab - b^2..........(1)

And

\\ (a+b)(x+y) = a^2 +b^2\\\Rightarrow (a+b)x+(a+b)y=a^2+b^2...........(2)

Now, Subtracting (1) from (2), we get

(a+b)x-(a-b)x=a^2+b^2-a^2+2ab+b^2

\Rightarrow(a+b-a+b)x=2b^2+2ab

\Rightarrow 2bx=2b(b+2a)

\Rightarrow x=(a+b)

Substituting this in (1), we get,

(a-b)(a+b)+(a+b)y=a^2-2ab-b^2

\Rightarrow a^2-b^2+(a+b)y=a^2-2ab-b^2

\Rightarrow (a+b)y=-2ab

\Rightarrow y=\frac{-2ab}{a+b} .

Hence,

x=(a+b),\:and\:y=\frac{-2ab}{a+b}

Q7 Solve the following pair of linear equations: (v) \\152x - 378y = -74\\ -378x + 152y = -604

Answer:

Given Equations,

\\152x - 378y = -74............(1)\\ -378x + 152y = -604............(2)

As we can see by adding and subtracting both equations we can make our equations simple to solve.

So,

Adding (1) and )2) we get,

-226x-226y=-678

\Rightarrow x+y=3...........(3)

Subtracting (2) from (1) we get,

530x-530y=530

\Rightarrow x-y=1...........(4)

Now, Adding (3) and (4) we get,

2x=4

\Rightarrow x=2

Putting this value in (3)

2+y=3

\Rightarrow y=1

Hence,

x=2\:and\:y=1

Q8 ABCD is a cyclic quadrilateral (see Fig. 3.7). Find the angles of the cyclic quadrilateral.

Answer:

As we know that in a quadrilateral the sum of opposite angles is 180 degrees.

So, From Here,

4y+20-4x=180

\Rightarrow 4y-4x=160

\Rightarrow y-x=40............(1)

Also,

3y-5-7x+5=180

\Rightarrow 3y-7x=180........(2)

Multiplying (1) by 3 we get,

\Rightarrow 3y-3x=120........(3)

Now,

Subtracting, (2) from (3) we get,

4x=-60

\Rightarrow x=-15

Substituting this value in (1) we get,

y-(-15)=40

\Rightarrow y=40-15

\Rightarrow y=25

Hence four angles of a quadrilateral are :

\angle A =4y+20=4(25)+20=100+20=120^0

\angle B =3y-5=3(25)-5=75-5=70^0

\angle C =-4x=-4(-15)=60^0

\angle D =-7x+5=-7(-15)+5=105+5=110^0

Class 10 Maths Chapter 3 Topics

  • Solving a linear equation with two variables.

  • Representation of linear equation in a graph.

  • Solutions of linear equations using the graph.

  • Algebraic interpretation of linear equations.

  • Formation of linear equations using statements.

Also get the solutions exercise wise-

SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Key Features of NCERT Class 10 Maths Solutions Chapter 3

  • The questions and their answers given in Chapter 3 Class 10 Maths NCERT solutions are very interesting and important for board and competitive exams.
  • NCERT solutions for Maths chapter 3 Linear Equations in Two Variables Class 10 will help to boost preparation for all of the examinations.

  • Many real-life situations can be formulated using Mathematical equations given in this chapter 3 NCERT Class 10 Maths solutions.

  • For example, consider the statement "cost of 1 Kg Apple and 2Kg orange is 120 and the cost of 3 Kg Apple and 1 Kg orange is 210". The statement can be formulated using the Mathematical equation, for this consider the cost of Apple as x and that of orange as y. Then we can write two equations as x+2y=120 and 3x+y=210.

NCERT Books and NCERT Syllabus

NCERT Solutions for Class 10 Maths - Chapter Wise

NCERT Solutions of Class 10 - Subject Wise

NCERT Exemplar solutions - Subject wise

How to use NCERT Solutions for Class 10 Maths Chapter 3?

Follow the given tips to make the most of NCERT solutions Class 10 Maths Chapter 3 PDF download:

  • NCERT solutions Class 10 Maths Chapter 3 are the most important tool when you are appearing for board examinations. 90% paper of CBSE board examinations, directly come from the NCERT.

  • Now you have done the NCERT solutions for Class 10 Maths chapter 3 and learned the approach to solving questions in the step by step method.

  • After covering Linear Equations in Two Variables Class 10 solutions you should target the past year papers of CBSE board examinations. The previous year papers will cover the rest 10% part of the Class 10 board exams.

Frequently Asked Question (FAQs)

1. What is a pair of linear equations in two variables Class 10 Maths?

In Class 10 Maths, a pair of linear equations in two variables is a set of two linear equations that contain two variables, typically represented by x and y. Linear equations are equations of the form ax + by = c, where a, b, and c are constants.

2. How can I obtain the solutions for Chapter 3 maths Class 10?

Students can find NCERT solutions for maths to class 10 linear equations in two variables above in this article. Our experts in simple and easy format develop these maths class 10 chapter 3 pair of linear equations in two variables class 10 solutions. These will be very helpful for students.

3. Is it necessary to work through all of the questions provided in the NCERT solutions for class 10 Chapter 3 maths?

It is very important to go through Class 10 maths linear equations in two variables questions as they are designed to help you understand the material and practice your problem-solving skills. Students can find ch 3 maths class 10 ncert solutions at careers360 official website. However, it is not necessarily required to work through class 10 chapter 3 maths solutions by every question in order to understand the concepts covered in the chapter.

4. What key concepts are covered in the NCERT solutions for Chapter 3 Class 10 Maths?

NCERT class chapter 3 pair of linear equations in two variables class 10 solutions

Contains the concepts of pairs of linear equations and solving them using methods like graphing method, substitution method, elimination method, Consistency and inconsistency of a pair of linear equations, and Dependent and independent linear equations. As  Class 10 linear equations in two variables questions are used to solve real-world problems.

5. What are the most crucial questions for ch3 maths class 10 linear equations in two variables?

In chapter 3 Pair of linear equations class 10 Exercise 3.1, Question 1 is important. All questions in Exercise 3.2 are important. In Exercise 3.3, Question 1 (parts iv, v, vi), Question 2, and Question 3 are important. Exercise 3.4's Question 2 is important, and Exercise 3.5's Questions 2 and 4 are important. All questions in Exercise 3.6 are important. All questions in the optional Exercise 3.7 are important. Students can download a pair of linear equations in two variables class 10 pdf.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:04 May,2024 - 04 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

CBSE Class 9, 10 Odia Syllabus 2024-25

146+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
hindi 10th class mp board sample paper

Dear aspirant !

Hope you are doing well ! The class 10 Hindi mp board sample paper can be found on the given link below . Set your time and give your best in the sample paper it will lead to great results ,many students are already doing so .

https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://school.careers360.com/download/sample-papers/mp-board-10th-hindi-model-paper&ved=2ahUKEwjO3YvJu5KEAxWAR2wGHSLpAiQQFnoECBMQAQ&usg=AOvVaw2qFFjVeuiZZJsx0b35oL1x .

Hope you get it !

Thanking you

Read Complete Answer
Shivanshu 04 February,2024
CBSE class 10th date sheet 11/1/2024 2024

Hello aspirant,

The dates of the CBSE Class 10th and Class 12 exams are February 15–March 13, 2024 and February 15–April 2, 2024, respectively. You may obtain the CBSE exam date sheet 2024 PDF from the official CBSE website, cbse.gov.in.

To get the complete datesheet, you can visit our website by clicking on the link given below.

https://school.careers360.com/boards/cbse/cbse-date-sheet

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 12 January,2024
iam in 7 th plz send 7th previous paper

Hello aspirant,

The paper of class 7th is not issued by respective boards so I can not find it on the board's website. You should definitely try to search for it from the website of your school and can also take advise of your seniors for the same.

You don't need to worry. The class 7th paper will be simple and made by your own school teachers.

Thank you

Hope it helps you.

Read Complete Answer
Sajal Trivedi 25 October,2023
my son's dob is 13/02/2009 is hi eligible for 10th board exam in 2024,,from cbse. olz reply me

The eligibility age criteria for class 10th CBSE is 14 years of age. Since your son will be 15 years of age in 2024, he will be eligible to give the exam.

Read Complete Answer
Shubhangi 29 July,2022
can Hindi marks be replace with IT 402(additional subject) in CBSE class 10th board

That totally depends on what you are aiming for. The replacement of marks of additional subjects and the main subject is not like you will get the marks of IT on your Hindi section. It runs like when you calculate your total percentage you have got, you can replace your lowest marks of the main subjects from the marks of the additional subject since CBSE schools goes for the best five marks for the calculation of final percentage of the students.

However, for the admission procedures in different schools after 10th, it depends on the schools to consider the percentage of main five subjects or the best five subjects to admit the student in their schools.

Read Complete Answer
Aditi Singh 22 July,2022
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
1 days ago :
March 22, 2024 - 08:12 PM IST :
February 02, 2024 - 03:47 PM IST :
CBSE Results 2024: Fake notice goes viral about Class 10th; official dates yet to be announced
May 01, 2024 - 07:45 AM IST
CBSE Class 10, 12 syllabus 2024-25 out; board restores two-level mathematics rule
March 22, 2024 - 08:01 PM IST
CBSE Class 10 board exam 2024 passing criteria, eligibility for compartment; all you need to know
March 20, 2024 - 08:38 PM IST
CBSE directs Class 10, 12 board exam centre superintendents to update OECMS portals
March 13, 2024 - 07:23 PM IST
CBSE Class 10 Computer Applications, IT, AI 2024 Exam Live: Paper analysis, answer key, result date, updates
March 12, 2024 - 03:45 PM IST
CBSE 2024 Maths Exam Live: CBSE Class 10 Mathematics answer key, paper analysis, passing marks, latest updates
March 10, 2024 - 06:18 PM IST
CBSE Class 10 mathematics paper 2024 tomorrow; exam pattern, timings
March 10, 2024 - 07:15 AM IST

Stay up-to date with CBSE Class 10th News

Back to top