Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • School
  • The angle of elevation of an aeroplane from point a on the ground is 60 degree after a flight of 10 seconds on the same height the angle of elevation from point a becomes 30 degree if the aeroplane

The angle of elevation of an aeroplane from point A on the ground is 60 degrees. After a flight of 10 seconds at the same height, the angle of elevation from point A becomes 30 degrees if the aeroplane is flying at the speed of 720 km per hour. Find the constant height at which the aeroplane is flying.

Answers (1)

best_answer

From the figure given below:

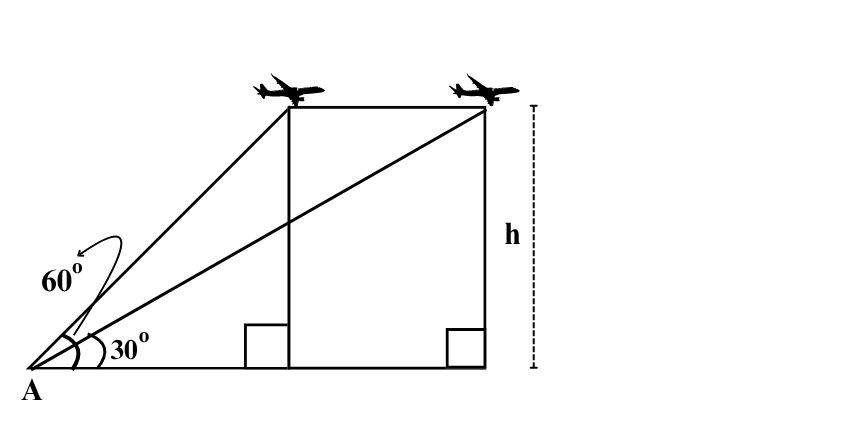
Let the plane’s height be $h$. 
From point $A$, the horizontal distances to the plane at the two observations are $x_1 = \dfrac{h}{\sqrt{3}}$ (when angle is $60^\circ$) and $x_2 = h\sqrt{3}$ (when angle is $30^\circ$).
So the horizontal distance the plane covers in $10,$s is
$x_2-x_1 = h\sqrt{3}-\dfrac{h}{\sqrt{3}} = \dfrac{2h}{\sqrt{3}}.$
Given speed $720\ \text{km/h} = 200\ \text{m/s}$, so distance in $10,$s is $200\times10=2000\ \text{m}$.
Now, on putting both the distances equal, to find the value of $h$, we have,
$\displaystyle \frac{2h}{\sqrt{3}} = 2000 \quad\Rightarrow\quad h = \frac{2000\sqrt{3}}{2} = 1000\sqrt{3}.$
Hence, the constant height at which the aeroplane is flying is $1000\sqrt{3}\ \text{m}\approx 1732.05\ \text{m}$.

Posted by

Komal Miglani

View full answer

Similar Questions

Trending Articles/News

anam-khan

CBSE 10th final date sheet 2026 out; exams till March 10, minor revisions after student protest
anam-khan

CBSE Board Exam 2026: Two exams for Class 10 ‘exhausting’ for teachers, cause more anxiety for students

Latest Question