Get Answers to all your Questions

Filter By

Clear Filter

All Questions

If 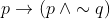$p\rightarrow \left ( p\: \wedge \sim q \right )$ is false, then the truth values of p and q are respectively :
Option: 1 F, T
Option: 2 T, F
Option: 3 F, F
Option: 4 T, T

Relation Between Set Notation and Truth Table -

Sets can be used to identify basic logical structures of statements. Statements have two fundamental roles either it is true or false.

Let us understand with an example of two sets p{1,2} and q{2,3}.

$\begin{array}{|c|c|c|}\hline\quad p\vee q\quad & \quad p\cup q\quad&\quad 1,2,3\quad \\ \hline p\wedge q& p\cap q&2 \\ \hline p^c& \sim p & 3,4 \\ \hline q^c& \sim q&1,4 \\ \hline\end{array}$

Using this relation we get

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline \text{Element } & \mathrm{\;\;\;\;\;}p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}q\mathrm{\;\;\;}&\mathrm{\;\;\;\;\;}\sim p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}\sim q\mathrm{\;\;\;} &\mathrm{\;\;\;}p\wedge q\mathrm{\;\;}&\mathrm{\;\;}p\vee q\mathrm{\;\;}&\sim\left (p\wedge q \right )\mathrm{\;\;}&\sim p\wedge\sim q\mathrm{\;\;} \\ \hline \hline 1& \mathrm{T}&\mathrm{F} & \mathrm{F} &\mathrm{T}&\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline2& \mathrm{T}&\mathrm{T} & \mathrm{F} &\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F}&\mathrm{T} \\ \hline 3& \mathrm{F}&\mathrm{T} & \mathrm{T} &\mathrm{F}&\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline4& \mathrm{F}&\mathrm{F} & \mathrm{T} &\mathrm{T}&\mathrm{F}&\mathrm{F}&\mathrm{T}&\mathrm{F} \\ \hline\end{array}$

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \rightarrow(\mathbf{p} \mathbf{\Lambda}-\mathbf{q}))} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline \mathbf{T} & {F} & {\mathbf{T}} \\ \hline \mathbf{T} & {T} & {F}\end{array}$

Correct Option (4)

View Full Answer(1)

Posted by

avinash.dongre

The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If now the mean age of the teachers in this school is 39 years, then the age (in years) of the newly appointed teacher is :
Option: 1 25
Option: 2 30
Option: 3 35
Option: 4 40

No concept add

mean age $= 40$ years

$\frac{\sum x_{i}}{25} = 40$ years

= sum of ages $\left ( s \right )$

new teacher be of age $T$ let the

now $\frac{S-60+T}{25}=39$

$1000-60+T=25\times 39$

$940+T=975$

$T=35\ years$

View Full Answer(1)

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

Which one of the following is a tautology ?

Option: 1 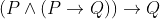$\left ( P\wedge \left ( P\rightarrow Q \right ) \right )\rightarrow Q$
Option: 2 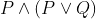$P\wedge (P\vee Q)$
Option: 3 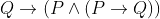$Q\rightarrow (P\wedge (P\rightarrow Q))$
Option: 4 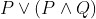$P\vee (P\wedge Q)$

Tautology And Contradiction -

Tautology

A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example, ( p ⇒ q ) ∨ ( q ⇒ p )

Contradiction (fallacy)

A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )

Truth Table

$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \mathrm{\;\;\;\;\;}p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}q\mathrm{\;\;\;}&\mathrm{\;\;\;\;\;}p\rightarrow q\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;} q\rightarrow p\mathrm{\;\;\;} &\mathrm{\;\;\;}\left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right )\mathrm{\;\;}&\mathrm{\;\;\;}\sim\left ( \left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right ) \right ) \mathrm{\;\;} \\\hline \hline \mathrm{T}&\mathrm{T} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{T}&\mathrm{F} & \mathrm{F} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{T} & \mathrm{T} &\mathrm{F}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{F} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline\end{array}$

Quantifiers

Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases.

For example –

p : For every prime number x, √x is an irrational number.

q : There exists a triangle whose all sides are equal.

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \rightarrow \mathbf{q})} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline T & {F} & {F} \\ \hline T & {T} & {\mathbf{T}}\end{array}$ $\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \wedge \mathbf{q})} \\ \hline F & {F} & {\mathbf{F}} \\ \hline F & {T} & {F} \\ \hline T & {F} & {F} \\ \hline T & {T} & {T}\end{array}$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(p \wedge(p \rightarrow q)) \rightarrow q} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline T & {F} & {T} \\ \hline T & {T} & {\mathbf{T}}\end{array}$

Correct Option (1)

View Full Answer(1)

Posted by

Kuldeep Maurya

The logical statement $(p\Rightarrow q)\wedge (q\Rightarrow \sim p)$ is equivalent to :
Option: 1 $\sim p$
Option: 2 $p$
Option: 3 $q$
Option: 4 $\sim q$

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|ccc}{\mathbf{p}} & {\mathbf{q}} & {((\mathbf{p} \rightarrow \mathbf{q})} & {\mathbf{\wedge}(\mathbf{q} \rightarrow \neg \mathbf{p}))} & {} \\ \hline F & {F} & {} & {\mathbf{T}} \\ \hline F & {T} & {} & {\mathbf{T}} \\ \hline T & {F} & {} & {F} \\ \hline T & {T} & {} & {F}\end{array}$

which is equal to $\sim p$

Correct Option (1)

View Full Answer(1)

Posted by

Ritika Jonwal

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Which of the following statements is a tautology ?
Option: 1 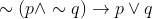$\sim (p\wedge \sim q)\rightarrow p\vee q$
Option: 2 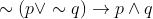$\sim (p\vee \sim q)\rightarrow p\wedge q$
Option: 3 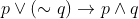$p\vee (\sim q)\rightarrow p\wedge q$
Option: 4 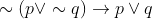$\sim (p\vee \sim q)\rightarrow p\vee q$

Tautology And Contradiction -

Tautology

A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example, ( p ⇒ q ) ∨ ( q ⇒ p )

Contradiction (fallacy)

A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )

Truth Table

Quantifiers

Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases.

For example –

p : For every prime number x, √x is an irrational number.

q : There exists a triangle whose all sides are equal.

Practise Session - 1 -

Q1. Write the negations of the following:
1. Ram is a doctor or peon.
2. Room is clean and big.
3. $\sqrt 5$ is a rational number.
4. If Ram is a doctor then he is smart

$\sim(p \vee \sim q) \rightarrow p \vee q$

$\begin{array}{l}{(\sim p \wedge q) \rightarrow(p \vee q)} \\ {\sim\{(\sim p \wedge q) \wedge(\sim p \wedge \sim q)\}} \\ {\sim\{\sim p \wedge f\}}\end{array}$

Correct Option (4)

View Full Answer(1)

Posted by

vishal kumar

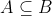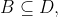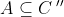Let A,B,C and D be four non-empty sets. The contrapositive statement of '' If $A\subseteq B$ and $B\subseteq D,$ then $A\subseteq C\: ''$ is :
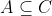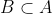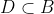
Option: 1 If $A\subseteq C$ , then $B\subset A$ or $D\subset B$
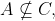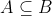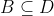
Option: 2 If $A\nsubseteq C,$ then $A\subseteq B$ and $B\subseteq D$
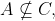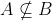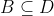
Option: 3 If $A\nsubseteq C,$ , then $A\nsubseteq B$ and $B\subseteq D$
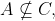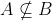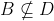
Option: 4 If $A\nsubseteq C,$ , then $A\nsubseteq B$ and $B\nsubseteq D$

Converse, Inverse, and Contrapositive -

Given an if-then statement "if p , then q ," we can create three related statements:

A conditional statement consists of two parts, a hypothesis in the “if” clause and a conclusion in the “then” clause. For instance, “If you are born in some country, then you are a citizen of that country”

"you are born in some country" is the hypothesis.

"you are a citizen of that country" is the conclusion.

To form the contrapositive of the conditional statement, interchange the hypothesis and the conclusion of the inverse statement.

The Contrapositive of “If you are born in some country, then you are a citizen of that country”

is “If you are not a citizen of that country, then you are not born in some country.”

$\begin{array}{|c|c|c|}\hline \text { \;\;Statement\;\; } & \mathrm{\;\;\;}{\text { If } p, \text { then } q} \mathrm{\;\;\;}& \mathrm{\;\;\;}p\rightarrow q \mathrm{\;\;\;}\\ \hline \text { Converse } & \mathrm{\;\;\;}{\text { If } q, \text { then } p} \mathrm{\;\;\;}&\mathrm{\;\;\;}q\rightarrow p \mathrm{\;\;\;} \\ \hline \text { Inverse } & \mathrm{\;\;\;}{\text { If not } p, \text { then not } q} \mathrm{\;\;\;}& \mathrm{\;\;\;}(\sim p) \rightarrow(\sim q) \mathrm{\;\;\;} \\ \hline \text { Contrapositive } & \mathrm{\;\;\;}{\text { If not } q, \text { then not } p} \mathrm{\;\;\;}& \mathrm{\;\;\;}(\sim q) \rightarrow(\sim p) \mathrm{\;\;\;}\\ \hline\end{array}$

$\\\text { Let } P=A \subseteq B, Q=B \subseteq D, R=A \subseteq C\\\text{contrapositive of }(P\wedge Q)\rightarrow R\;\text{ is}\\\sim R \rightarrow \sim (P\wedge Q)\\\text{i.e.}\;\;\;\sim R\rightarrow (\sim P\vee \sim Q)$

Hence, $\text { If } A \nsubseteq C, \text { then } A \nsubseteq B \text { or } B \not \neq D$

Correct Option (4)

View Full Answer(1)

Posted by

Ritika Jonwal

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

Which of the following is equivalent to the Boolean expression 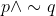$p \wedge \sim q$ ?

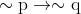
Option: 1 $\sim \mathrm{p} \rightarrow \sim \mathrm{q}$
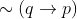
Option: 2 $\sim(q \rightarrow p)$
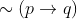
Option: 3 $\sim(p \rightarrow q)$
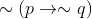
Option: 4 $\sim(p \rightarrow \sim q)$

Option 1 . $\sim p\rightarrow \sim q$
            $\equiv \sim \left ( \sim p \right )\vee \sim q$
           $= p\vee \sim q$
Option 2. $\sim \left ( q\rightarrow p \right )$
            $\equiv \sim \left ( \sim q\vee p \right )$
           $\equiv q\wedge \sim p$
Option 3. $\sim \left ( p\rightarrow q \right )$
$\equiv \sim \left ( \sim p\vee q \right )$
$\equiv p\wedge \sim q$
so option (3)

View Full Answer(1)

Posted by

Kuldeep Maurya

Negation of the statement 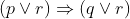$(p \vee r) \Rightarrow(q \vee r)$ is :
Option: 1 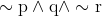$\sim \mathrm{p} \wedge \mathrm{q} \wedge \sim \mathrm{r}$
Option: 2 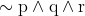$\sim \mathrm{p} \wedge \mathrm{q} \wedge \mathrm{r}$
Option: 3 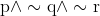$\mathrm{p} \wedge \sim \mathrm{q} \wedge \sim \mathrm{r}$
Option: 4 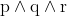$\mathrm{p} \wedge \mathrm{q} \wedge \mathrm{r}$

$p\Rightarrow q\\$ is equivalent to $\sim p \vee q$

So $\sim\left ( p\Rightarrow q \right )\equiv \left ( p\wedge\sim q \right )\\$

$\Rightarrow \sim((p \vee r) \Rightarrow(q \vee r)) \equiv(p \vee r) \wedge\sim\left ( q \vee r \right ) \\$

$\equiv (p \vee r) \wedge(\sim q \wedge \sim r) \\$

$\equiv ((p \vee r) \wedge(\sim r)) \wedge \sim q \\$

$\equiv (p \wedge \sim r) \vee(r \wedge \sim r) \wedge \sim q$

$\equiv p\wedge \sim r\wedge\sim q$

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

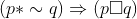Let $, \square \in\{\wedge , \vee]$ be such that the Boolean expression $(p \sim q) \Rightarrow(p \square q)$ is a tautology. Then :
Option: 1 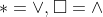$=\vee,\square=\wedge$
Option: 2 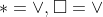$ =\vee, \square=\vee$
Option: 3 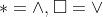$* =\wedge, \square=\vee$
Option: 4 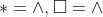$* =\wedge, \square=\wedge$

Tautology is a statement in which all the outcomes are True.
To Make max True in $p\rightarrow q$ , p should be contain maximum False statements.
so $try \: \ast = \wedge \, and\,\: \square = \vee$
$\left ( p\wedge \sim q \right )\Rightarrow \left ( p\vee q \right )$
Truth Table

p	q	$\sim q$	$p\wedge \sim q$	$p\vee q$	$\left ( p\wedge \sim q \right )\Rightarrow \left ( p\vee q \right )$
T	T	F	F	T	T
T	F	T	T	T	T
F	T	F	F	T	T
F	F	T	F	F	T

Option (3)

View Full Answer(1)

Posted by

Kuldeep Maurya

The Boolean expression 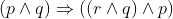$(p \wedge q) \Rightarrow((r \wedge q) \wedge p)$ is equivalent to :
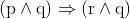
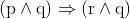
Option: 1 $(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \wedge \mathrm{q})$
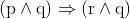
Option: 2 $(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \wedge \mathrm{q})$
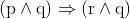
Option: 3 $(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \wedge \mathrm{q})$
Option: 4 $(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \wedge \mathrm{q})$
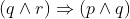
Option: 5 $(q \wedge r) \Rightarrow(p \wedge q)$
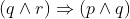
Option: 6 $(q \wedge r) \Rightarrow(p \wedge q)$
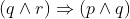
Option: 7 $(q \wedge r) \Rightarrow(p \wedge q)$
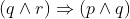
Option: 8 $(q \wedge r) \Rightarrow(p \wedge q)$
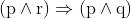
Option: 9 $(\mathrm{p} \wedge \mathrm{r}) \Rightarrow(\mathrm{p} \wedge \mathrm{q})$
Option: 10 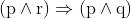$(\mathrm{p} \wedge \mathrm{r}) \Rightarrow(\mathrm{p} \wedge \mathrm{q})$
Option: 11 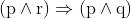$(\mathrm{p} \wedge \mathrm{r}) \Rightarrow(\mathrm{p} \wedge \mathrm{q})$
Option: 12 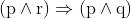$(\mathrm{p} \wedge \mathrm{r}) \Rightarrow(\mathrm{p} \wedge \mathrm{q})$
Option: 13 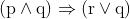$(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \vee \mathrm{q})$
Option: 14 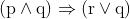$(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \vee \mathrm{q})$
Option: 15 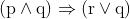$(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \vee \mathrm{q})$
Option: 16 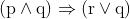$(\mathrm{p} \wedge \mathrm{q}) \Rightarrow(\mathrm{r} \vee \mathrm{q})$

Truth Table

$p$	$q$	$r$	$p\wedge q$	$(r\wedge q)\wedge p$	$(p\wedge q)\Rightarrow ((r\wedge q)\wedge p)$	$r\wedge q$	$( p\wedge q )\Rightarrow(r\wedge q)$
$T$	$T$	$T$	$T$	$T$	$T$	$T$	$T$
$T$	$T$	$F$	$T$	$F$	$F$	$F$	$F$
$T$	$F$	$F$	$F$	$F$	$T$	$F$	$T$
$T$	$F$	$F$	$F$	$F$	$T$	$F$	$T$
$F$	$T$	$T$	$F$	$F$	$T$	$T$	$T$
$F$	$T$	$F$	$F$	$F$	$T$	$F$	$T$
$F$	$F$	$T$	$F$	$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$	$F$	$T$	$F$	$T$

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Top Schools

Products & Resources

NCERT Solutions

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

If is false, then the truth values of p and q are respectively : Option: 1 F, TOption: 2 T, F Option: 3 F, F Option: 4 T, T

Posted by

avinash.dongre

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

Which one of the following is a tautology ? Option: 1 Option: 2 Option: 3 Option: 4

Posted by

Kuldeep Maurya

The logical statement is equivalent to : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

Ritika Jonwal

JEE Main high-scoring chapters and topics

Which of the following statements is a tautology ?Option: 1 Option: 2 Option: 3 Option: 4

Posted by

If $p\rightarrow \left ( p\: \wedge \sim q \right )$ is false, then the truth values of p and q are respectively :
Option: 1 F, T
Option: 2 T, F
Option: 3 F, F
Option: 4 T, T

Which one of the following is a tautology ?

Option: 1 $\left ( P\wedge \left ( P\rightarrow Q \right ) \right )\rightarrow Q$
Option: 2 $P\wedge (P\vee Q)$
Option: 3 $Q\rightarrow (P\wedge (P\rightarrow Q))$
Option: 4 $P\vee (P\wedge Q)$

The logical statement $(p\Rightarrow q)\wedge (q\Rightarrow \sim p)$ is equivalent to :
Option: 1 $\sim p$
Option: 2 $p$
Option: 3 $q$
Option: 4 $\sim q$

Which of the following statements is a tautology ?
Option: 1 $\sim (p\wedge \sim q)\rightarrow p\vee q$
Option: 2 $\sim (p\vee \sim q)\rightarrow p\wedge q$
Option: 3 $p\vee (\sim q)\rightarrow p\wedge q$
Option: 4 $\sim (p\vee \sim q)\rightarrow p\vee q$

Which of the following is equivalent to the Boolean expression $p \wedge \sim q$ ?

Option: 1 $\sim \mathrm{p} \rightarrow \sim \mathrm{q}$
Option: 2 $\sim(q \rightarrow p)$
Option: 3 $\sim(p \rightarrow q)$
Option: 4 $\sim(p \rightarrow \sim q)$

Let $, \square \in\{\wedge , \vee]$ be such that the Boolean expression $(p \sim q) \Rightarrow(p \square q)$ is a tautology. Then :
Option: 1 $=\vee,\square=\wedge$
Option: 2 $ =\vee, \square=\vee$
Option: 3 $* =\wedge, \square=\vee$
Option: 4 $* =\wedge, \square=\wedge$