Get Answers to all your Questions

Filter By

Clear Filter

All Questions

Read the passage below and answer the following questions.

Cheating is considered a criminal offence under the Indian Penal Code. It is done to gain profit or advantage from another person by using some deceitful means. The person who deceives another knows for the fact that it would place the other person in an unfair situation. Cheating as an offence can be made punishable under Section 420 of the IPC. Scope of Section 415 Cheating is defined under Section 415 of the Indian Penal Code as whoever fraudulently or dishonestly deceives a person to induce that person to deliver a property to any person or to consent to retain any property. If a person intentionally induces a person to do or omit to do any act which he would not have done if he was not deceived to do so and the act has caused harm to that person in body, mind, reputation, or property, then the person who fraudulently, dishonestly or intentionally induced the other person is said to cheat. Any dishonest concealment of facts that can deceive a person to do an act that he would not have done otherwise is also cheating within the meaning of this section. Essential Ingredients of Cheating requires · deception of any person. Fraudulently or dishonestly inducing that person to deliver any property to any person or to consent that any person shall retain any property; or · intentionally inducing a person to do or omit to do anything which he would not do or omit if he were not so deceived, and the act or omission causes or is likely to cause damage or harm to that person in body, mind, reputation or property.

Deceit– a tort arising from an untrue or false statement of facts which are made by a person, recklessly or knowingly, with an intention that it shall be acted upon by the other person, who would suffer damages as a result.

Fraud – a false or untrue representation of the fact, that is made with the knowledge of its falsity or without the belief in its truth or a reckless statement that may or may not be true, with an intention to induce a person or individual to act independent of it with the result that the person acts on it and suffers damages and harm. In other words, it is a wrong act or criminal deception with an intention to result in financial or personal gain.

Question :- D went to a moneylender, Z, for the loan. D intentionally pledges the gold article with Z taking the loan. D knows that the article is not made of gold. After a few days, D leaves the village. Decide.
Option: 1
-

Option: 2
D has committed cheating as well as fraud

Option: 3
D has not committed the offence of cheating

Option: 4
D has committed an act which is an offence of cheating as well as the tort of deceit

As per section 415 of IPC, D has intentionally pledged the gold article with Z, his intention is clearly to deceive Z and cause him financial loss hence D would be liable for the offence of Cheating. Actions of D are also held liable as a tort of deceit.

Hence option (d) is correct.

View Full Answer(1)

Posted by

Rishabh Jain

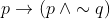If $p\rightarrow \left ( p\: \wedge \sim q \right )$ is false, then the truth values of p and q are respectively :
Option: 1 F, T
Option: 2 T, F
Option: 3 F, F
Option: 4 T, T

Relation Between Set Notation and Truth Table -

Sets can be used to identify basic logical structures of statements. Statements have two fundamental roles either it is true or false.

Let us understand with an example of two sets p{1,2} and q{2,3}.

$\begin{array}{|c|c|c|}\hline\quad p\vee q\quad & \quad p\cup q\quad&\quad 1,2,3\quad \\ \hline p\wedge q& p\cap q&2 \\ \hline p^c& \sim p & 3,4 \\ \hline q^c& \sim q&1,4 \\ \hline\end{array}$

Using this relation we get

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline \text{Element } & \mathrm{\;\;\;\;\;}p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}q\mathrm{\;\;\;}&\mathrm{\;\;\;\;\;}\sim p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}\sim q\mathrm{\;\;\;} &\mathrm{\;\;\;}p\wedge q\mathrm{\;\;}&\mathrm{\;\;}p\vee q\mathrm{\;\;}&\sim\left (p\wedge q \right )\mathrm{\;\;}&\sim p\wedge\sim q\mathrm{\;\;} \\ \hline \hline 1& \mathrm{T}&\mathrm{F} & \mathrm{F} &\mathrm{T}&\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline2& \mathrm{T}&\mathrm{T} & \mathrm{F} &\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F}&\mathrm{T} \\ \hline 3& \mathrm{F}&\mathrm{T} & \mathrm{T} &\mathrm{F}&\mathrm{F}&\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline4& \mathrm{F}&\mathrm{F} & \mathrm{T} &\mathrm{T}&\mathrm{F}&\mathrm{F}&\mathrm{T}&\mathrm{F} \\ \hline\end{array}$

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \rightarrow(\mathbf{p} \mathbf{\Lambda}-\mathbf{q}))} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline \mathbf{T} & {F} & {\mathbf{T}} \\ \hline \mathbf{T} & {T} & {F}\end{array}$

Correct Option (4)

View Full Answer(1)

Posted by

avinash.dongre

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If now the mean age of the teachers in this school is 39 years, then the age (in years) of the newly appointed teacher is :
Option: 1 25
Option: 2 30
Option: 3 35
Option: 4 40

No concept add

mean age $= 40$ years

$\frac{\sum x_{i}}{25} = 40$ years

= sum of ages $\left ( s \right )$

new teacher be of age $T$ let the

now $\frac{S-60+T}{25}=39$

$1000-60+T=25\times 39$

$940+T=975$

$T=35\ years$

View Full Answer(1)

Posted by

vishal kumar

Which one of the following is a tautology ?

Option: 1 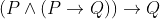$\left ( P\wedge \left ( P\rightarrow Q \right ) \right )\rightarrow Q$
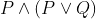
Option: 2 $P\wedge (P\vee Q)$
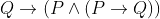
Option: 3 $Q\rightarrow (P\wedge (P\rightarrow Q))$
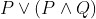
Option: 4 $P\vee (P\wedge Q)$

Tautology And Contradiction -

Tautology

A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example, ( p ⇒ q ) ∨ ( q ⇒ p )

Contradiction (fallacy)

A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )

Truth Table

$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \mathrm{\;\;\;\;\;}p\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;}q\mathrm{\;\;\;}&\mathrm{\;\;\;\;\;}p\rightarrow q\mathrm{\;\;\;\;\;}&\mathrm{\;\;\;} q\rightarrow p\mathrm{\;\;\;} &\mathrm{\;\;\;}\left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right )\mathrm{\;\;}&\mathrm{\;\;\;}\sim\left ( \left ( p\rightarrow q \right )\vee\left ( q\rightarrow p \right ) \right ) \mathrm{\;\;} \\\hline \hline \mathrm{T}&\mathrm{T} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{T}&\mathrm{F} & \mathrm{F} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{T} & \mathrm{T} &\mathrm{F}&\mathrm{T}&\mathrm{F} \\ \hline \mathrm{F}&\mathrm{F} & \mathrm{T} &\mathrm{T}&\mathrm{T}&\mathrm{F} \\ \hline\end{array}$

Quantifiers

Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases.

For example –

p : For every prime number x, √x is an irrational number.

q : There exists a triangle whose all sides are equal.

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \rightarrow \mathbf{q})} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline T & {F} & {F} \\ \hline T & {T} & {\mathbf{T}}\end{array}$ $\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(\mathbf{p} \wedge \mathbf{q})} \\ \hline F & {F} & {\mathbf{F}} \\ \hline F & {T} & {F} \\ \hline T & {F} & {F} \\ \hline T & {T} & {T}\end{array}$

$\begin{array}{c|c|c}{\mathbf{p}} & {\mathbf{q}} & {(p \wedge(p \rightarrow q)) \rightarrow q} \\ \hline F & {F} & {\mathbf{T}} \\ \hline F & {T} & {\mathbf{T}} \\ \hline T & {F} & {T} \\ \hline T & {T} & {\mathbf{T}}\end{array}$

Correct Option (1)

View Full Answer(1)

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

The logical statement $(p\Rightarrow q)\wedge (q\Rightarrow \sim p)$ is equivalent to :
Option: 1 $\sim p$
Option: 2 $p$
Option: 3 $q$
Option: 4 $\sim q$

Practise Session - 2 -

Q1. Write the truth table for the following statement pattern:
$\\ \mathrm{1.\;\;\;\sim(p \vee((\sim q \Rightarrow q) \wedge q))}\\\mathrm{2.\;\;\;(p\wedge q)\vee(\sim r)}\\$

$\begin{array}{c|c|ccc}{\mathbf{p}} & {\mathbf{q}} & {((\mathbf{p} \rightarrow \mathbf{q})} & {\mathbf{\wedge}(\mathbf{q} \rightarrow \neg \mathbf{p}))} & {} \\ \hline F & {F} & {} & {\mathbf{T}} \\ \hline F & {T} & {} & {\mathbf{T}} \\ \hline T & {F} & {} & {F} \\ \hline T & {T} & {} & {F}\end{array}$

which is equal to $\sim p$

Correct Option (1)

View Full Answer(1)

Posted by

Ritika Jonwal

Which of the following statements is a tautology ?
Option: 1 $\sim (p\wedge \sim q)\rightarrow p\vee q$
Option: 2 $\sim (p\vee \sim q)\rightarrow p\wedge q$
Option: 3 $p\vee (\sim q)\rightarrow p\wedge q$
Option: 4 $\sim (p\vee \sim q)\rightarrow p\vee q$

Tautology And Contradiction -

Tautology

A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example, ( p ⇒ q ) ∨ ( q ⇒ p )

Contradiction (fallacy)

A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )

Truth Table

Quantifiers

Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases.

For example –

p : For every prime number x, √x is an irrational number.

q : There exists a triangle whose all sides are equal.

Practise Session - 1 -

Q1. Write the negations of the following:
1. Ram is a doctor or peon.
2. Room is clean and big.
3. $\sqrt 5$ is a rational number.
4. If Ram is a doctor then he is smart

$\sim(p \vee \sim q) \rightarrow p \vee q$

$\begin{array}{l}{(\sim p \wedge q) \rightarrow(p \vee q)} \\ {\sim\{(\sim p \wedge q) \wedge(\sim p \wedge \sim q)\}} \\ {\sim\{\sim p \wedge f\}}\end{array}$

Correct Option (4)

View Full Answer(1)

Posted by

vishal kumar

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

Let A,B,C and D be four non-empty sets. The contrapositive statement of '' If $A\subseteq B$ and $B\subseteq D,$ then $A\subseteq C\: ''$ is :
Option: 1 If $A\subseteq C$ , then $B\subset A$ or $D\subset B$
Option: 2 If $A\nsubseteq C,$ then $A\subseteq B$ and $B\subseteq D$
Option: 3 If $A\nsubseteq C,$ , then $A\nsubseteq B$ and $B\subseteq D$
Option: 4 If $A\nsubseteq C,$ , then $A\nsubseteq B$ and $B\nsubseteq D$

Converse, Inverse, and Contrapositive -

Given an if-then statement "if p , then q ," we can create three related statements:

A conditional statement consists of two parts, a hypothesis in the “if” clause and a conclusion in the “then” clause. For instance, “If you are born in some country, then you are a citizen of that country”

"you are born in some country" is the hypothesis.

"you are a citizen of that country" is the conclusion.

To form the contrapositive of the conditional statement, interchange the hypothesis and the conclusion of the inverse statement.

The Contrapositive of “If you are born in some country, then you are a citizen of that country”

is “If you are not a citizen of that country, then you are not born in some country.”

$\begin{array}{|c|c|c|}\hline \text { \;\;Statement\;\; } & \mathrm{\;\;\;}{\text { If } p, \text { then } q} \mathrm{\;\;\;}& \mathrm{\;\;\;}p\rightarrow q \mathrm{\;\;\;}\\ \hline \text { Converse } & \mathrm{\;\;\;}{\text { If } q, \text { then } p} \mathrm{\;\;\;}&\mathrm{\;\;\;}q\rightarrow p \mathrm{\;\;\;} \\ \hline \text { Inverse } & \mathrm{\;\;\;}{\text { If not } p, \text { then not } q} \mathrm{\;\;\;}& \mathrm{\;\;\;}(\sim p) \rightarrow(\sim q) \mathrm{\;\;\;} \\ \hline \text { Contrapositive } & \mathrm{\;\;\;}{\text { If not } q, \text { then not } p} \mathrm{\;\;\;}& \mathrm{\;\;\;}(\sim q) \rightarrow(\sim p) \mathrm{\;\;\;}\\ \hline\end{array}$

$\\\text { Let } P=A \subseteq B, Q=B \subseteq D, R=A \subseteq C\\\text{contrapositive of }(P\wedge Q)\rightarrow R\;\text{ is}\\\sim R \rightarrow \sim (P\wedge Q)\\\text{i.e.}\;\;\;\sim R\rightarrow (\sim P\vee \sim Q)$

Hence, $\text { If } A \nsubseteq C, \text { then } A \nsubseteq B \text { or } B \not \neq D$

Correct Option (4)

View Full Answer(1)

Posted by

Ritika Jonwal

The IUPAC name of the following comound is:
Option: 1 5-Bromo-3-methylcyclopentanoic acid
Option: 2 4-Bromo-2-methylcyclopentane carboxylic acid
Option: 3 3-Bromo-5-methylcyclopentanoic acid
Option: 4 3-Bromo-5-methylcyclopentane carboxylic acid

-COOH group has more seniority than others.

At 2 branched carbon preferred.

At 4 there is Br

So, counting will be

So, IUPAC Name

4-Bromo-2-methylcyclopentane carboxylic acid

Therefore, the correct option is (2).

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

Which of the following is equivalent to the Boolean expression $p \wedge \sim q$ ?

Option: 1 $\sim \mathrm{p} \rightarrow \sim \mathrm{q}$
Option: 2 $\sim(q \rightarrow p)$
Option: 3 $\sim(p \rightarrow q)$
Option: 4 $\sim(p \rightarrow \sim q)$

Option 1 . $\sim p\rightarrow \sim q$
            $\equiv \sim \left ( \sim p \right )\vee \sim q$
           $= p\vee \sim q$
Option 2. $\sim \left ( q\rightarrow p \right )$
            $\equiv \sim \left ( \sim q\vee p \right )$
           $\equiv q\wedge \sim p$
Option 3. $\sim \left ( p\rightarrow q \right )$
$\equiv \sim \left ( \sim p\vee q \right )$
$\equiv p\wedge \sim q$
so option (3)