Get Answers to all your Questions

Filter By

Clear Filter

All Questions

5 g of Na₂SO₄ was dissolved in x g of H₂O. The change in freezing point was found to be 3.82⁰C. If Na₂SO₄ is 81.5% ionised, the value of x (K $f$ for water=1.86⁰C kg mol⁻¹) is approximately : (molar mass of S=32 g mol⁻¹ and that of Na=23 g mol⁻¹)
Option: 1 15 g
Option: 2 25 g
Option: 3 45 g
Option: 4 65 g

View Full Answer(1)

Posted by

vishal kumar

The freezing point of benzene decreases by 0.45⁰C when 0.2 g of acetic acid is added to 20 g of benzene. If acetic acid associates to form a dimer in benzene, percentage association of acetic acid in benzene will be : (K_f for benzene=5.12 K kg mol⁻¹)
Option: 1 74.6%
Option: 2 94.6
Option: 3 64.6%
Option: 4 80.4%

In benzene ,

$2 CH_{3}COOH \rightleftharpoons \left ( CH_{3}COOH \right )_{2}$

t = 0 1 -

t = t 1 - $\beta$ $\frac{\beta }{2}$

Given:

w = 0.2g W = 20 g $\Delta$ T = 0.45 K

As we know , $\Delta T = \frac{1000 \times K_{f} \times w}{M \times W }$

$\Delta T = \frac{1000 \times 5.12 \times 0.2}{M \times 20 }= 0.45$

$\therefore$ , observed M = 113.78 (acetic acid)

Molecular weight of acetic acid = 60

$i =\frac{normal \; molecular \; mass}{observed \; molecular \; mass}$

$\therefore \frac{m_{normal}}{m_{observed}} = 1 - \beta + \frac{\beta }{2}$

$\frac{60}{113.78} = 1 - \beta + \frac{\beta }{2}$

$\Rightarrow \beta = 0.945$

% degree of association = 94.5 %

View Full Answer(1)

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

At room temperature, a dilute solution of urea is prepared by dissolving 0.60g of urea in 360 g of water. If the vapour pressure of pure water at this temperature is 35 mmHg, lowering of vapour pressure(in mmHg) will be: (molar mass of urea = 60g/mol)
Option: 1 0.017
Option: 2 0.028
Option: 3 0.027
Option: 4 0.031

Molecular weight of urea = 60 g / mol

Now, we know that :

Relative lowering of vapour pressure is equal to the molar mass of the solute.

$\therefore \Delta P=35\times\frac{(\frac{0.6}{60})}{\frac{360}{18}+\frac{0.6}{60}}$

$\Delta P=35\times\frac{0.01}{20+0.01}$

$\Delta P=35\times0.00049$

$\Delta P=0.0174 \: mm Hg$

$\therefore$ option (1) is correct.

View Full Answer(1)

Posted by

Ritika Jonwal

The elevation of boiling point of 0.1 m aq $CrCl_{3}.xNH_{3}$ solution is two times that of 0.05 aq. $CaCl_{2}$ solution. The value of x _____ (Assume 100% ionization of complex and $CaCl_{2}$ , coordination number of Cr is 6 and that all of $NH_{3}$ molecules are present inside the coordination sphere.)

$\mathrm{\Delta T_{b}\; of \;CrCl_{3}.xNH_{3}= 2(\Delta T_{b}\; of \; CaCl_{2})}$

$i \times 0.1 = 2 \times 3 \times 0.05$

Thus, i = 3

Therefore, the complex is dissociated into 3 ions.

Hence, complex is $[Cr(NH_{3})_{5}Cl]Cl_{2}$

Thus, the value is 5.

View Full Answer(1)

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

A set of solutions is prepared using 180 g of water as a solvent and 10 g of different non-volatile solutes A,B and C. The relative lowring of vapour pressure in the presence of these solutes are in the order [Given, molar mass of A=100 g mol ^-1; B=200 g mol ^-1; C=10,000 g mol ^-1]
Option: 1 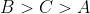$B>C>A$
Option: 2 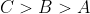$C>B>A$
Option: 3 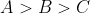$A>B>C$
Option: 4 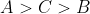$A>C>B$

Here vapour pressure of water is lowering.

We know this formula,

Partial Vapour pressure of water P_water = P^oXwater

Lowering Vapour pressure of water = P^o – P_water

The relative lowering of vapour pressure $\mathrm{=\frac{P^o-P}{P^o}}=\mathrm{\frac{\Delta P}{P^o}} =1- \chi_{water}$

$\mathrm{\mathrm{\frac{\Delta P}{P^o}} =\chi_{solute}=\frac{\frac{m_{solute}}{M_{solute}}}{\frac{m_{solute}}{M_{solute}}+\frac{m_{water}}{M_{water}}}}$

Now,

$\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{A}}=\frac{\frac{10}{100}}{\frac{10}{100}+\frac{180}{18}}$

$\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{B}}=\frac{\frac{10}{200}}{\frac{10}{200}+\frac{180}{18}}$

$\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{C}}=\frac{\frac{10}{10,000}}{\frac{10}{10,000}+\frac{180}{18}}$

From above,

$\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{A}}>\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{B}}>\left(\frac{\Delta \mathrm{P}}{\mathrm{P}^{0}}\right)_{\mathrm{C}}$

View Full Answer(1)

Posted by

Kuldeep Maurya

How much amount of NaCl (in grams) should be added to 600g of water to decrease the freezing point of water to $-0.2^{\circ}C$ ? (Assume that the freezing point depression constant for water = 2K kg mol^-1)
Option: 1 1.76
Option: 2 3.52
Option: 3 4.9
Option: 4 8.58

$\begin{array}{l}{\Delta \mathrm{T}_{\mathrm{f}}=0.2^{\circ} \mathrm{C}} \\ {\Delta \mathrm{T}_{\mathrm{f}}=\mathrm{ik_{f}m}} \\ {0.2=2 \times 2 \times \frac{w}{58.5} \times \frac{1000}{600}} \\\\ {w=\frac{0.2 \times 58.5 \times 600}{1000 \times 4}} {=\frac{1.2 \times 58.5}{40}=1.76 \mathrm{g}}\end{array}$

View Full Answer(1)

Posted by

avinash.dongre

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

The osmotic pressure of a solution of NaCl is 0.10 atm and that of a glucose solution is 0.20 atm. The osmotic pressure of a solution formed by mixing 1L of the sodium chloride solution 2L of the glucose solution is $\mathrm{x \times 10^{-3}atm}$ . x is _________ (nearest interger)

We know this formula.

$\mathrm{ \pi_{f} v_{f}=\pi_{1} v_{1}+\pi_{2} v_{2} }$

$\mathrm{ \pi_{f} =\frac{\pi_{1} v_{1}+\pi_{2} v_{2}}{v_f} }$

$\mathrm{ \pi_{f} = \frac{0.1 \times 1+0.2 \times 2}{3} }$

$\mathrm{ \pi_{f} =\frac{0.5}{3}=\frac{500}{3} \times 10^{-3} }$

$\mathrm{ x =167 }$

Ans = 167

------------------------------------------

Alternate Solution

$\mathrm{ x =167 }$

Ans = 167

View Full Answer(1)

Posted by

Kuldeep Maurya

The mole fraction of glucose $(C_{6}H_{12}O_{6})$ in an aqueous binary solution is 0.1. The mass percentage of water in it to the nearest integer is-

Mole fraction of glucose, in $C_{6}H_{12}O_{6}=0.1$

Now, lets assume we have 10 moles of solution.

Thus, moles of $C_{6}H_{12}O_{6}=1$

Ans, moles of $H_2O = 9$

Now, the mass of water = number of moles x molar mass

Thus, the mass of water $\mathrm{= 9 \times 18 = 162 \ g}$

Mass of $C_{6}H_{12}O_{6}=180\: gm$

Now, mass percent of water is given as:

$\mathrm{Mass\: \%\: of\: water\: =\: \frac{Mass\: of\: water}{Mass\: of\: water\: +\: mass\: of\: glucose}\: x\: 100}$

$\mathrm{Mass\: \%\: of\: water\: =\: \frac{162}{180 +\: 162}\: x\: 100}$

$\mathrm{Mass\: \%\: of\: water\: =\: 47.3\%}$

Thus, the correct answer is 47.

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

If $250\; cm^{3}$ of an aqueous solution containing $0.73\; g$ of a protein A is isotonic with one litre of another aqueous solution containing $1.65\; g$ of a protein $B$ , AT $298\; K$ , the ratio of the molecular masses of $A$ and $B$ is ______ $\times 10^{-2}$ (to the nearest integer).

Let molar mass of protein A = x g/mol
Let molar mass of protein B = y g/mol

$\pi_{\mathrm{A}}=\text { osmotic pressure of protein } \mathrm{A}=\frac{\left(\frac{0.73}{\mathrm{x}}\right)}{0.25} \mathrm{RT}$

$\pi_{\mathrm{B}}=\text { osmotic pressure of protein } \mathrm{B}=\frac{\left(\frac{1.65}{\mathrm{y}}\right)}{1} \mathrm{RT}$

Now, $\pi_{\mathrm{A}}=\pi_{\mathrm{B}}$

$\left(\frac{0.73}{\mathrm{x} \times 0.25}\right) \mathrm{RT}=\left(\frac{1.65}{\mathrm{y}}\right) \mathrm{RT}$

$\left(\frac{\mathrm{x}}{\mathrm{y}}\right)=\frac{0.73}{0.25 \times 1.65}=1.769 \cong 1.77$

$\mathrm{\frac{x}{y} = 177 \times 10^{-2}}$

Ans = 177

View Full Answer(1)

Posted by

Kuldeep Maurya

2 molal solution of a weak acid HA has a freezing point of 3.885^oC. The degree of dissociation of this acid is _________ $\times 10^{-3}.$ (Round off to the Nearest Integer). [Given : Molal depression constant of water $\mathrm{=1.85\; K\; kg\; mol^{-1}}$ Freezing point of pure water = 0^o C]

Given,

2 molal solution of a weak acid HA has a freezing point of 3.885ºC.

$\mathrm{T}_{\mathrm{f} \text { sol. }}=3.885^{\circ} \mathrm{C}$

m = 2

Molal depression constant of water (K_f) = 1.85 K kg mol^-1

The freezing point of pure water T_i = 0ºC

van't Hoff factor i is related to the degree of dissociation \alpha $\alpha$ as, if n = number of ions,

$\alpha=\frac{i-1}{n-1}$

Here n = 2 (H⁺and A^-)

So,

$i = 1+\alpha$

We know the formula of depression at the freezing point.

$\mathrm{\Delta T = i\times K_f\times m}$

$\mathrm{\Delta T = T_f -T_i= i\times K_f\times m}$

$3.885 - 0= i\times 1.85\times 2$

i = 1.05

Now,

$i = 1+\alpha$

$1.05 = 1+\alpha$

$\alpha=0.05$

$\alpha=50\times10^{-3}$

Ans = 50

View Full Answer(1)

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Ranking

Products & Resources

NCERT Solutions

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Animation Courses

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

Posted by

vishal kumar

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

Posted by

Ritika Jonwal

The elevation of boiling point of 0.1 m aq solution is two times that of 0.05 aq. solution. The value of x _____ (Assume 100% ionization of complex and , coordination number of Cr is 6 and that all of molecules are present inside the coordination sphere.)

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Posted by

Kuldeep Maurya

How much amount of NaCl (in grams) should be added to 600g of water to decrease the freezing point of water to ? (Assume that the freezing point depression constant for water = 2K kg mol-1) Option: 1 1.76 Option: 2 3.52 Option: 3 4.9 Option: 4 8.58

Posted by

How much amount of NaCl (in grams) should be added to 600g of water to decrease the freezing point of water to $-0.2^{\circ}C$ ? (Assume that the freezing point depression constant for water = 2K kg mol^-1)
Option: 1 1.76
Option: 2 3.52
Option: 3 4.9
Option: 4 8.58

The osmotic pressure of a solution of NaCl is 0.10 atm and that of a glucose solution is 0.20 atm. The osmotic pressure of a solution formed by mixing 1L of the sodium chloride solution 2L of the glucose solution is $\mathrm{x \times 10^{-3}atm}$ . x is _________ (nearest interger)

The mole fraction of glucose $(C_{6}H_{12}O_{6})$ in an aqueous binary solution is 0.1. The mass percentage of water in it to the nearest integer is-

If $250\; cm^{3}$ of an aqueous solution containing $0.73\; g$ of a protein A is isotonic with one litre of another aqueous solution containing $1.65\; g$ of a protein $B$ , AT $298\; K$ , the ratio of the molecular masses of $A$ and $B$ is ______ $\times 10^{-2}$ (to the nearest integer).

2 molal solution of a weak acid HA has a freezing point of 3.885^oC. The degree of dissociation of this acid is _________ $\times 10^{-3}.$ (Round off to the Nearest Integer). [Given : Molal depression constant of water $\mathrm{=1.85\; K\; kg\; mol^{-1}}$ Freezing point of pure water = 0^o C]