Get Answers to all your Questions

Filter By

Clear Filter

All Questions

The value of $\cos ^{3}\left ( \frac{\pi }{8} \right )\cdot \cos \left ( \frac{3\pi }{8} \right )+\sin ^{3}\left ( \frac{\pi }{8} \right )\cdot \sin \left ( \frac{3\pi }{8} \right )$ is :
Option: 1 $\frac{1}{4}$

Option: 2 $\frac{1}{2\sqrt{2}}$

Option: 3 $\frac{1}{2}$

Option: 4 $\frac{1}{\sqrt{2}}$

Trigonometric Identities -

Trigonometric Identities-

These identities are the equations that hold true regardless of the angle being chosen.

$\\\mathrm{\sin^2\mathit{t}+\cos^2\mathit{t}=1}\\\mathrm{1+\tan^2\mathit{t}=\sec^2\mathit{t}}\\\mathrm1+{\cot^2\mathit{t}=\csc^2\mathit{t}}\\\mathrm{\tan \mathit{t}=\frac{\sin \mathit{t}}{\cos \mathit{t}},\;\;\cot \mathit{t}=\frac{\cos\mathit{t}}{\sin\mathit{t}}}$

Allied Angles (Part 1) -

Allied Angles (Part 1)

Two angles or numbers are called allied iff their sum or difference is a multiple of π/2

sin (90⁰ - θ) = cos (θ)
cos (90⁰ - θ) = sin (θ)
tan (90⁰ - θ) = cot (θ)
csc (90⁰ - θ) = sec (θ)
sec (90⁰ - θ) = csc (θ)
cot (90⁰ - θ) = tan (θ)

sin (90⁰ + θ) = cos (θ)
cos (90⁰ + θ) = - sin (θ)
tan (90⁰ + θ) = - cot (θ)
csc (90⁰ + θ) = sec (θ)
sec (90⁰ + θ) = - csc (θ)
cot (90⁰ + θ) = - tan (θ)

$\\\cos ^3\:\frac{\pi }{8}\cos \frac{3\:\pi }{8}+\sin ^3\frac{\pi }{8}\:\sin \frac{3\:\pi }{8}\\\sin\left ( \frac{\pi}{2}-\frac{3\pi}{8} \right )=\cos\left ( \frac{3\pi}{8} \right )=\sin\left ( \frac{\pi}{8} \right )\\\\\\\cos ^3\:\frac{\pi }{8}\sin \frac{\:\pi }{8}+\sin ^3\frac{\pi }{8}\:\cos \frac{\:\pi }{8}\\\sin\frac{\pi}{8}\cos\frac{\pi}{8}\left ( \cos ^2\:\frac{\pi }{8}+\sin ^2\:\frac{\pi }{8} \right )\\\frac{1}{2}\left ( 2\:\sin \frac{\pi }{8}\cos \:\frac{\pi \:}{8} \right )=\frac{1}{2}\:\sin \frac{2\pi }{8}=\frac{1}{2\sqrt2}$

View Full Answer(1)

Posted by

avinash.dongre

If $\frac{\sqrt{2}\sin \alpha }{\sqrt{1+\cos 2\alpha }}=\frac{1}{7}$ and $\sqrt{\frac{1-\cos 2\beta }{2}}=\frac{1}{\sqrt{10}},$ $\alpha ,\beta\; \epsilon \left ( 0,\frac{\pi }{2} \right ),$ then $\tan \left ( \alpha +2\beta \right )$ is equal to ________.
Option: 1 $0$
Option: 2 $1$
Option: 3 $0.5$
Option: 4 $2$

Trigonometric Identities -

Trigonometric Identities-

These identities are the equations that hold true regardless of the angle being chosen.

Double Angle Formula and Reduction Formula -

Double Angle Formula and Reduction Formula

$\begin{aligned} \sin (2 \theta) &=2 \sin \theta \cos \theta \\&=\frac{2\tan\theta}{1+\tan^2\theta} \\\cos (2 \theta) &=\cos ^{2} \theta-\sin ^{2} \theta \\ &=1-2 \sin ^{2} \theta \\ &=2 \cos ^{2} \theta-1\\&=\frac{1-\tan^2\theta}{1+\tan^2\theta} \\ \tan (2 \theta) &=\frac{2 \tan \theta}{1-\tan ^{2} \theta} \end{aligned}$

$\begin{aligned} \tan (\alpha+\beta) &=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\ \tan (\theta+\theta) &=\frac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta} \\ \tan (2 \theta) &=\frac{2 \tan \theta}{1-\tan ^{2} \theta} \end{aligned}$

$\\\frac{\sqrt{2} \sin \alpha}{\sqrt{2} \cos \alpha}=\frac{1}{7}\\\tan\alpha=\frac{1}{7}\\\sin\beta=\frac{1}{\sqrt{10}}\\\tan\beta=\frac{1}{\sqrt{3}}\\\tan 2 \beta=\frac{2 \cdot \frac{1}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4}\\\tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta}=1$

Correct Option (2)

View Full Answer(1)

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

Two poles, $A B$ of length a metres and $C D$ of length $a+b(b \neq a)$ metres are erected at the same horizontal level with bases at $\mathrm{B}$ and $\mathrm{D}$ . If $\mathrm{BD}=x$ and $\tan \angle \mathrm{ACB}=\frac{1}{2}$ , then :
Option: 1 $x^{2}-2 \mathrm{a} x+\mathrm{a}(\mathrm{a}+\mathrm{b})=0$
Option: 2 $x^{2}+2(\mathrm{a}+2 \mathrm{~b}) x-\mathrm{b}(\mathrm{a}+\mathrm{b})=0$
Option: 3 $x^{2}+2(\mathrm{a}+2 \mathrm{~b}) x+\mathrm{a}(\mathrm{a}+\mathrm{b})=0$
Option: 4 $x^{2}-2 \mathrm{a} x+\mathrm{b}(\mathrm{a}+\mathrm{b})=0$

$\angle ACB= \angle ACD-\angle BCD\\$

$\Rightarrow \tan\angle ACB=\tan\left ( \angle ACD-\angle BCD \right )\\$

$\tan\angle ACD= \frac{x}{b}, \tan\angle BCD= \frac{x}{a+b}\\$

$\Rightarrow \frac{1}{2}= \frac{\frac{x}{b}-\frac{x}{a+b}}{1+\frac{x}{b}\cdot \frac{x}{a+b}}\\$

$\Rightarrow \frac{1}{2}= \frac{\left ( a+b \right )x-bx}{b\left ( a+b \right )+x^{2}}\\$

$\Rightarrow x^{2}-2ax+b\left ( a+b \right )= 0$

View Full Answer(1)

Posted by

Kuldeep Maurya

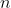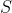If $n$ is the number of solutions of the equation $2 \cos x\left(4 \sin \left(\frac{\pi}{4}+x\right) \sin \left(\frac{\pi}{4}-x\right)-1\right)=1$, $x \in[0, \pi]$ and $S$ is the sum of all these solutions, then the ordered pair 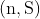$(\mathrm{n}, \mathrm{S})$ is
Option: 1 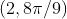$(2,8 \pi / 9)$
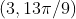
Option: 2 $(3,13 \pi / 9)$
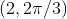
Option: 3 $(2,2 \pi / 3)$
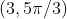
Option: 4 $(3,5 \pi / 3)$

$2\cos x\left [ 4\left ( \sin ^{2} \frac{\pi }{4}-\sin ^{2}x\right ) -1\right ]= 1$
$\Rightarrow 2\cos x\left [ 4\left ( \frac{1}{2} -\sin ^{2}x\right )-1\right ]= 1$
$\Rightarrow 2\cos x\left [2-4\sin ^{2}x-1\right ]= 1$
$\Rightarrow 2\cos x\left [1-4\sin ^{2}x\right ]= 1$
$\Rightarrow 2\cos x\left [1-4+4\cos ^{2}x\right ]= 1$
$\Rightarrow 2\cos x\left [4\cos ^{2}x-3\right ]= 1$
$\Rightarrow 2\left ( 4\cos ^{3}x-3\cos x \right )= 1$
$\Rightarrow \cos 3x= \frac{1}{2}$
$\Rightarrow 3x= \frac{\pi }{3},\frac{5\pi }{3},\frac{7\pi }{3}$
$\Rightarrow x= \frac{\pi }{9},\frac{5\pi }{9},\frac{7\pi }{9}$
$\Rightarrow n= 3,S= \frac{13\pi }{9}$

View Full Answer(1)

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

The range of the function
$f(x)=\log _{\sqrt{5}}\left(3+\cos \left(\frac{3 \pi}{4}+x\right)+\cos \left(\frac{\pi}{4}+x\right)+\cos \left(\frac{\pi}{4}-x\right)-\cos \left(\frac{3 \pi}{4}-x\right)\right)$ is
Option: 1 $\left[\frac{1}{\sqrt{5}}, \sqrt{5}\right]$
Option: 2 $[0,2]$
Option: 3 $(0, \sqrt{5})$
Option: 4 $[-2,2]$

$f(x)=\log _{\sqrt{5}}\left ( 3+\cos \left ( \frac{3 \pi}{4} \right )\cos x-\sin \left ( \frac{3 \pi}{4} \right )\sin x+\cos \left ( \frac{ \pi}{4} \right )\cos x-\sin \left ( \frac{ \pi}{4} \right ) \cdot \sin x+\cos \left ( \frac{ \pi}{4} \right )\cos x+\sin \left ( \frac{ \pi}{4} \right )\cdot \sin x-\cos \left ( \frac{3 \pi}{4} \right )\cos x-\sin \left ( \frac{3 \pi}{4} \right )\sin x\right )$
$=\log _{\sqrt{5}}\left ( 3+2\cdot \cos \left ( \frac{\pi}{4} \right )\cos x-2\sin \left ( \frac{3\pi}{4} \right )\sin x \right )$
$=\log _{\sqrt{5}}\left ( 3+\sqrt{2}\left ( \cos x-\sin x \right ) \right )$
$Now\, -\sqrt{2}\leq \cos x-\sin x\leq \sqrt{2}$
$-2\leq \sqrt{2} \left ( \cos x-\sin x \right )\leq 2$
$1\leq3+ \sqrt{2} \left ( \cos x-\sin x \right )\leq 5$
$\log _{\sqrt{5}}\left ( 1 \right )\leq \log _{\sqrt{5}}\left ( 3+\sqrt{2} \left ( \cos x-\sin x \right )\right )\leq \log _{\sqrt{5}}\left ( 5 \right )$
$0\leq f\left ( x \right )\leq 2$

$\therefore Range\, is\, \left [ 0,2\right ]$

View Full Answer(1)

Posted by

Kuldeep Maurya

$\cos ^{-1}(\cos (-5))+\sin ^{-1}(\sin (6))-\tan ^{-1}(\tan (12))$ is equal to : (The inverse trigonometric functions take the principal values)

Option: 1 $3 \pi+1$
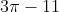
Option: 2 $3 \pi-11$
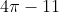
Option: 3 $4 \pi-11$
Option: 4 $4 \pi-9$

$\cos^{-1}\left ( \cos \left ( -5 \right ) \right )+\sin^{-1}\left ( \sin \left ( 6 \right ) \right )-\tan^{-1}\left ( \tan \left ( 12 \right ) \right )$ $= \cos^{-1}\left ( \cos \left ( 5 \right ) \right )+\sin^{-1}\left ( \sin \left ( 6 \right ) \right )-\tan^{-1}\left ( \tan \left ( 12 \right ) \right )$

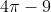
Using graphs of $y= T^{-1}\left ( T\left ( x \right ) \right )$

$= \left ( 2\pi -5 \right )+\left ( 6-2\pi \right )-\left ( 12-4\pi \right )$
$= 4\pi -11$

View Full Answer(1)

Posted by

Kuldeep Maurya

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

The domain of the function
$f(x)=\sin ^{-1}\left(\frac{3 x^{2}+x-1}{(x-1)^{2}}\right)+\cos ^{-1}\left(\frac{x-1}{x+1}\right)$ is :
Option: 1 $\left[0, \frac{1}{2}\right]$
Option: 2 $\left[0, \frac{1}{4}\right]$
Option: 3 $\left[\frac{1}{4}, \frac{1}{2}\right] \cup\{0\}$
Option: 4 $[-2,0] \cup\left[\frac{1}{4}, \frac{1}{2}\right]$

Domain

$-1\leq \frac{3x^{2}+x-1}{\left ( x-1 \right )^{2}}\leq 1;x\neq1\\$

$\Rightarrow -\left ( x-1 \right )^{2}\leq 3x^{2}+x-1\leq \left ( x-1 \right )^{2}\\$

$\Rightarrow 4x^{2}-x\geq 0\; and\; 2x^{2}+3x-2\leq 0\\$

$\Rightarrow 4x\left ( x-\frac{1}{4} \right )\geq 0\; and\; 2x^{2}+4x-x-2\leq 0\\$

$\Rightarrow x\in\left ( -\infty,0 \right ]\cup \left [\frac{1}{4},\infty \right )\; and\; x\in\left [ -2,\frac{1}{2} \right ]\\$

$So\; x\in\; \left [ -2,0 \right ]\cup \left [ \frac{1}{4},\frac{1}{2} \right ]\\$ ..........(1)

$Also\; -1\leq \frac{x-1}{x+1}\leq 1\Rightarrow \frac{x-1}{x+1}+1\geq 0\; and\; \frac{x-1}{x+1}-1\leq 0\\$

$\Rightarrow \frac{2x}{x+1}\geq 0\; and\; \frac{-2}{x+1}\leq 0\Rightarrow \frac{1}{x+1}\geq 0,x\neq -1\\$

$\Rightarrow x \in\left ( -\infty,-1 \right ]\cup \left [ 0,\infty \right )\; and \; x\in\left ( -1,\infty \right )\\$

$\Rightarrow x\in\left [ 0,\infty \right )$ .......(2)

From (1) and (2)

$x\in \{0\} \cup \left [ \frac{1}{4},\frac{1}{2} \right ]$

View Full Answer(1)

Posted by

Kuldeep Maurya

The number of solutions of the equation $32^{\tan ^{2} x}+32^{\sec ^{2} x}=81,0 \leq x \leq \frac{\pi}{4}$ is :
Option: 1 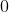$0$
Option: 2 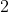$2$
Option: 3 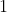$1$
Option: 4 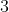$3$

$32^{\tan^{2}x}+32^{1+\tan^{2}x}= 81\\$

$32^{\tan^{2}x}=t\\$

$\Rightarrow t+32t=81\\$

$\Rightarrow 33t=81\Rightarrow t=\frac{81}{33}\\$

$\Rightarrow 32^{\tan^{2}x}=\frac{81}{33}=\frac{27}{11}\\$

$\Rightarrow \tan^{2}x=\log_{32}\frac{27}{11}\in\left ( 0,1 \right )\\$

$\Rightarrow x=\tan^{-1}\sqrt{\log_{32}\frac{27}{11}}For \; 0\leq x\leq \pi/4\\$

$\Rightarrow only\; 1 \; solution$

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

A vertical pole fixed to the horizontal ground is divided in the ratio 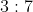$3: 7$ by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a point on the ground 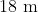$18 \mathrm{~m}$ away from the base of the pole, then the height of the pole (in meters) is :
Option: 1 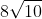$8 \sqrt{10}$
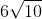
Option: 2 $6 \sqrt{10}$
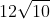
Option: 3 $12 \sqrt{10}$
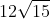
Option: 4 $12 \sqrt{15}$

$In\: \triangle ABC ;\tan \theta = \frac{3x}{18}= \frac{x}{6}---\left ( 1 \right )$
$In\: \triangle ABD ;\tan 2\theta = \frac{10x}{18}= \frac{5x}{9}$
$\Rightarrow \frac{2\tan \theta }{1-\tan ^{2}\theta }= \frac{5x}{9}$
$\Rightarrow \frac{2\times \frac{x}{6}}{1-\frac{x^{2}}{36}}= \frac{5x}{9}$
$\Rightarrow 108= 180-5x^{2}\Rightarrow 5x^{2}= 72$
$\Rightarrow x = 6\sqrt{\frac{2}{5}}\Rightarrow 10x = 6\sqrt{\frac{2}{5}}\times 10= 12\sqrt{10}$
option (3)

View Full Answer(1)

Posted by

Kuldeep Maurya

$\operatorname{cosec} 18^{\circ}$ is a root of the equation :
Option: 1 $x^{2}+2 x-4=0$
Option: 2 $4 x^{2}+2 x-1=0$
Option: 3 $x^{2}-2 x-4=0$
Option: 4 $x^{2}-2 x+4=0$

$\operatorname{cosec} 18^{\circ}= \frac{1}{\sin 18^{\circ}}= \frac{4}{\sqrt{5}-1}= \sqrt{5}+1= \alpha$
$Let\, \beta = 1-\sqrt{5}$
$\alpha +\beta = 2 ;\alpha \, \beta = -4$
$\Rightarrow x^{2}-2x-4= 0$
option (3)

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Ranking

Products & Resources

NCERT Solutions

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Animation Courses

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

The value of is : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

avinash.dongre

If and then is equal to ________. Option: 1 Option: 2 Option: 3 Option: 4

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

Two poles, of length a metres and of length metres are erected at the same horizontal level with bases at . If and , then : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

Kuldeep Maurya

If is the number of solutions of the equation and is the sum of all these solutions, then the ordered pair isOption: 1 Option: 2 Option: 3 Option: 4

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

The range of the function isOption: 1 Option: 2 Option: 3 Option: 4

$\cos ^{-1}(\cos (-5))+\sin ^{-1}(\sin (6))-\tan ^{-1}(\tan (12))$ is equal to : (The inverse trigonometric functions take the principal values)

Option: 1 $3 \pi+1$
Option: 2 $3 \pi-11$
Option: 3 $4 \pi-11$
Option: 4 $4 \pi-9$

The number of solutions of the equation $32^{\tan ^{2} x}+32^{\sec ^{2} x}=81,0 \leq x \leq \frac{\pi}{4}$ is :
Option: 1 $0$
Option: 2 $2$
Option: 3 $1$
Option: 4 $3$

$\operatorname{cosec} 18^{\circ}$ is a root of the equation :
Option: 1 $x^{2}+2 x-4=0$
Option: 2 $4 x^{2}+2 x-1=0$
Option: 3 $x^{2}-2 x-4=0$
Option: 4 $x^{2}-2 x+4=0$