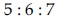Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- Home
- Engineering
- Help me solve this If the lengths of the sides of a triangle are in A.P. and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is :
If the lengths of the sides of a triangle are in A.P. and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is :
- Option 1)
- Option 2)
- Option 3)
- Option 4)
Answers (1)

Let be side of
is smallest angle
Three angles are,
Given,
Use sine rule.
Option 1)
Option 2)
Option 3)
Option 4)
View full answer
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Similar Questions
- 0.27 g of a long chain fatty acid was dissolved in 100 cm3 of hexane. 10 mL of this solution was added dropwise to the surface of water in a
- 0.3 g of acid is neutralised by 40 cm3 .125N NaOH .equvivalent mass of acid is
- 1. A block of mass 10 kg is kept on a rough inclined as shown in figure. The coefficient of friction between the block and the surface is 0