Browse by Stream
QnA
Home

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  •  India’s Mangalyan was sent to the Mars  by launching it into a transfer orbit EOM around the sun. It leaves the earth at E and meets Mars at M. If the semi-major axis of Earth&rsqu

 India’s Mangalyan was sent to the Mars  by launching it into a transfer orbit EOM around the sun. It leaves the earth at E and meets Mars at M. If the semi-major axis of Earth’s orbit is ae = 1.5\times1011 m, that of Mar’s orbit am = 2.28\times1011 m, taken Kepler’s laws give the estimate of time for Mangalyan to reach Mars from Earth to be close to : (In days)

Option: 1

260


Option: 2

320


Option: 3

500


Option: 4

220


Answers (1)

best_answer

As we discussed in

Kepler's 3rd law -

T^{2}\: \alpha\: a^{3}

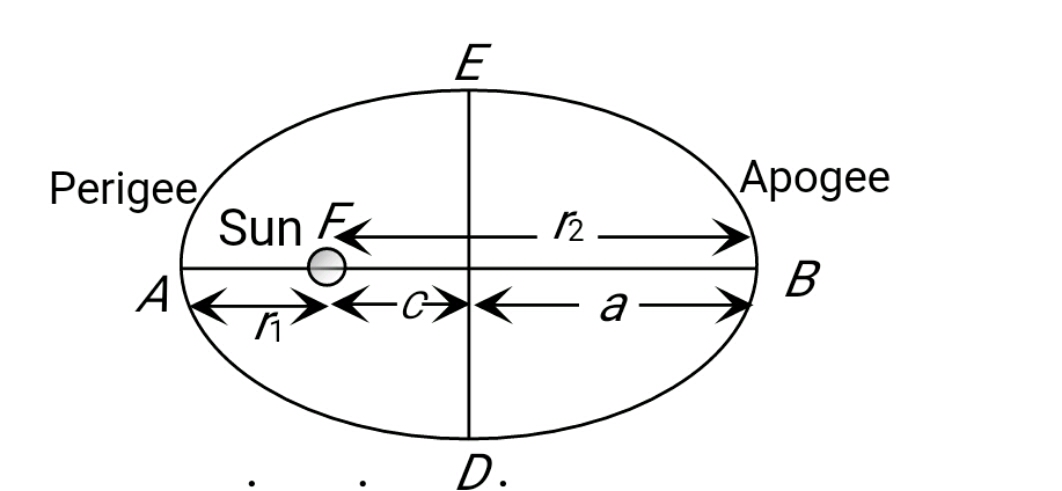
From fig.

 \therefore\; a=\frac{r_{1}+r_{1}}{2}

a= semi major Axis

r_{1}= Perigee

 r_{2}= apogee

For EOM  

 r_m=\frac{1.5+2.28}{2}=1.89

\frac{T_{m}}{T_{e}}=(\frac{1.89}{1.5})^{\frac{3}{2}}\:=> T_{m}=T_{e}*(\frac{1.89}{1.5})^{\frac{3}{2}}

time for Mangalyan to reach Mars from Earth=t=\frac{T_m}{2}

So t=\frac{365}{2}\times 1.41=257.3days

Posted by

shivangi.shekhar

View full answer

Similar Questions

Latest Question