Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- Home
- Engineering
- Two tangents are drawn from the point to the circle If these tangents touch the
Two tangents are drawn from the point  to the circle
to the circle  If these tangents touch the circle at points
If these tangents touch the circle at points  is a point on the circle such that length of the segments
is a point on the circle such that length of the segments  are equal, then the area of the triangle ABD is equal to
are equal, then the area of the triangle ABD is equal to
Option: 1 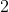
Option: 2 
Option: 3 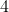
Option: 4 
Answers (1)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Similar Questions
Trending Articles/News
Latest Question
- X is to the south west of y, L is to East of x and southeast of y and m is to the north of L in line with xy in which direction of y and m is located
- A stone is allowed to fall from the top of the tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/ calculate when and where 2 stones will meet.




