Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 12 Maths Chapter 8 Application of integrals

NCERT Solutions for Class 12 Maths Chapter 8 Application of integrals

Edited By Ramraj Saini | Updated on Sep 14, 2023 10:14 PM IST | #CBSE Class 12th

NCERT Application Of Integrals Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals are discussed here. These NCERT solutions are created by expert team at Creers360 keeping in mind of latest syllabus of CBSE 2023-24. In geometry, you must have learned some formulas to calculate areas of simple geometrical figures like triangles, rectangles, trapeziums, circles, etc. But how do you calculate areas enclosed by curves? In this article, you will get NCERT solutions for class 12 maths chapter 8 application of integrals. This article also includes application of integrals class 12 solutions. Important topics that are going to be discussed in this chapter 8 class 12 maths are the area under simple curves, the area between lines and arcs of circles, parabolas, and ellipses. Interested students can find all NCERT Solutions for Class 12 Maths in one place

This Story also Contains
  1. NCERT Application Of Integrals Class 12 Questions And Answers
  2. NCERT Application Of Integrals Class 12 Questions And Answers PDF Free Download
  3. Application Of Integrals Class 12 NCERT Solutions - Important Formulae
  4. NCERT Application Of Integrals Class 12 Questions And Answers (Intext Questions and Exercise)
  5. Application of integrals class 12 - Topics
  6. NCERT solutions for class 12 maths - Chapter wise
  7. Key Features of NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals
  8. NCERT solutions for class 12 subject wise
  9. NCERT Solutions Class Wise
  10. NCERT Books and NCERT Syllabus

In the applications of integrals class 12 ncert solutions, questions from all these topics are covered. In this composition of Class 12 Maths Chapter 8 NCERT solutions application of integrals, you will learn some important applications of integrals class 12. If you are interested to check all NCERT solutions from classes 6 to 12 in a single place, which will help you to learn CBSE maths and science. Here you will get NCERT solutions for class 12.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

Also read:

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

NCERT Application Of Integrals Class 12 Questions And Answers PDF Free Download

Download PDF

Application Of Integrals Class 12 NCERT Solutions - Important Formulae

>> Area Enclosed by a Curve and Lines: The area enclosed by the curve y = f(x), the x-axis, and the lines x = a and x = b (where b > a) is given by the formula:

Area = ∫[a, b]y.dx = ∫[a, b]f(x).dx

>> Area Bounded by Curve and Horizontal Lines: The area of the region bounded by the curve x = φ(y) as its y-axis and the lines y = c and y = d is given by the formula: Area = ∫[c, d]x.dy = ∫[c, d]φ(y).dy

>> Area Between Two Curves and Vertical Lines: The area enclosed between two given curves y = f(x) and y = g(x), and the lines x = a and x = b is given by the formula:

Area = ∫[a, b][f(x) - g(x)].dx (Where f(x) ≥ g(x) in [a, b])

>> Area Between Curves with Different Intervals: If f(x) ≥ g(x) in [a, c] and f(x) ≤ g(x) in [c, b], where a < c < b, then the resultant area between the curves is given as:

Area = ∫[a, c][f(x) - g(x)].dx + ∫[c, b][g(x) - f(x)].dx

Free download Application Of Integrals Class 12 NCERT Solutions for CBSE Exam.

NCERT Application Of Integrals Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT class 12 maths chapter 8 question answer Exercise: 8.1

Question:1 Find the area of the region bounded by the curve y^2=x and the lines x=1,x=4 and the x -axis in the first quadrant.

Answer:

Area of the region bounded by the curve y^2=x and the lines x=1,x=4 and the x -axis in the first quadrant

Area = \int_{1}^{4}ydy = \int_{1}^{4}\sqrt{x}dx

\left [\frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]^4_1 = \frac{2}{3}\left [ (4)^\frac{3}{2}- (1)^\frac{3}{2} \right ]

= \frac{2}{3}\left [ 8 -1 \right ]

= 14/3 units

Question:2 Find the area of the region bounded by y^2=9x,x=2,x=4 and the x -axis in the first quadrant.

Answer:

Area of the region bounded by the curve y^2=9x,x=2,x=4 and the x -axis in the first quadrant

Area = \int_{2}^{4}ydy = \int_{2}^{4}\sqrt{9x}dx = 3\int_{2}^{4}\sqrt{x}dx

3\left [\frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]^4_2 = 3.\frac{2}{3}\left [ (4)^\frac{3}{2}- (2)^\frac{3}{2} \right ]

= 2\left [ 8 -2\sqrt2 \right ]

= \left [ 16 -4\sqrt2 \right ] units

Question:3 Find the area of the region bounded by x^2=4y,y=2,y=4 and the y -axis in the first quadrant.

Answer:

The area bounded by the curves x^2=4y,y=2,y=4 and the y -axis in the first quadrant is ABCD.


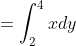
= \int^4_{2} x dy

= \int^4_{2} 2\sqrt{y} dy

= 2\int^4_{2} \sqrt{y} dy

=2\left \{ \frac{y^{\frac{3}{2}}}{\frac{3}{2}} \right \}^4_{2}

= \frac{4}{3}\left \{ (4)^{\frac{3}{2}}-(2)^{\frac{3}{2}} \right \}

= \frac{4}{3} \left \{ 8 -2\sqrt 2 \right \}

= \left \{ \frac{32-8\sqrt 2}{3} \right \}\ units.

Question:4 Find the area of the region bounded by the ellipse \frac{x^2}{16}+\frac{y^2}{9}=1.

Answer:

The area bounded by the ellipse : \frac{x^2}{16}+\frac{y^2}{9}=1.


1646972152541

Area will be 4 times the area of EAB.

Therefore, Area\ of\ EAB= \int^4_{0} y dx

= \int^4_{0}3\sqrt{1-\frac{x^2}{16}} dx

= \frac{3}{4}\int^4_{0}\sqrt{16-x^2} dx

= \frac{3}{4}\left [ \frac{x}{2}\sqrt{16-x^2}+\frac{16}{2}\sin^{-1}\frac{x}{4} \right ]^4_{0}

= \frac{3}{4}\left [ 2\sqrt{16-16} +8\sin^{-1}(1)-0-8\sin^{-1}(0)\right ]

= \frac{3}{4}\left [ \frac{8\pi}{2} \right ]

= \frac{3}{4}\left [ 4\pi \right ] =3\pi

Therefore the area bounded by the ellipse will be = 4\times {3\pi} = 12\pi\ units.

Question: 5 Find the area of the region bounded by the ellipse \small \frac{x^2}{4}+\frac{y^2}{9}=1

Answer:

The area bounded by the ellipse : \small \frac{x^2}{4}+\frac{y^2}{9}=1

1646972197883

The area will be 4 times the area of EAB.

Therefore, Area\ of\ EAB= \int^2_{0} y dx

= \int^2_{0}3\sqrt{1-\frac{x^2}{4}} dx

= \frac{3}{2}\int^2_{0}\sqrt{4-x^2} dx

= \frac{3}{2}\left [ \frac{x}{2}\sqrt4-x^2 +\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]^2_{0}

= \frac{3}{2}\left [ \frac{2\pi}{2} \right ]

= \frac{3\pi}{2}

Therefore the area bounded by the ellipse will be = 4\times \frac{3\pi}{2} = 6\pi\ units.

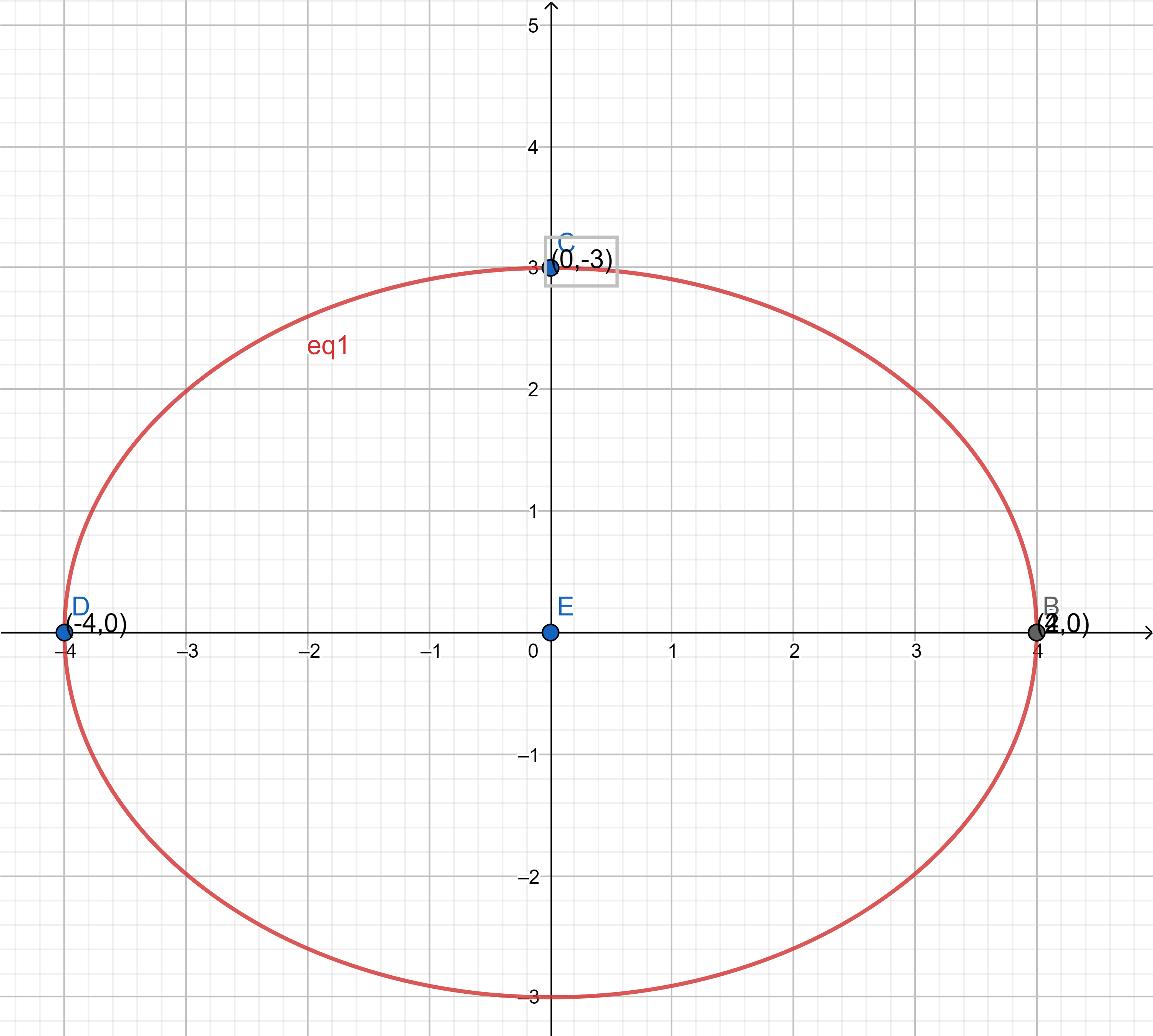
Question: 6 Find the area of the region in the first quadrant enclosed by \small x -axis, line \small x=\sqrt{3}y and the circle \small x^2+y^2=4
Answer:

The area of the region bounded by \small x=\sqrt{3}y and \small x^2+y^2=4 is ABC shown:

1646972234725

The point B of the intersection of the line and the circle in the first quadrant is (\sqrt3,1) .

Area ABC = Area ABM + Area BMC where, M is point in x-axis perpendicular drawn from the line.

Now,area of ABM = \frac{1}{2}\times AM\times BM = \frac{1}{2}\times \sqrt{3}\times 1 =\frac{\sqrt3}{2} ............(1)

and Area of BMC = \int^2_{\sqrt{3}} ydx

= \int^2_{\sqrt3} \sqrt{4-x^2} dx

= \left [ \frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]^2_{\sqrt3}

= \left [ 2\times\frac{\pi}{2}-\frac{\sqrt3}{2}\sqrt{4-3}-2\sin^{-1}\left ( \frac{\sqrt3}{2} \right ) \right ]

= \left [ \pi - \frac{\sqrt3\pi}{2}-2\frac{\pi}{3} \right ]

= \left [ \pi-\frac{\sqrt3}{2}-\frac{2\pi}{3} \right ]

= \left [ \frac{\pi}{3}-\frac{\sqrt3}{2} \right ] ..................................(2)

then adding the area (1) and (2), we have then

The Area under ABC = \frac{\sqrt3}{2} +\frac{\pi}{3}-\frac{\sqrt3}{2} = \frac{\pi}{3}\ units.

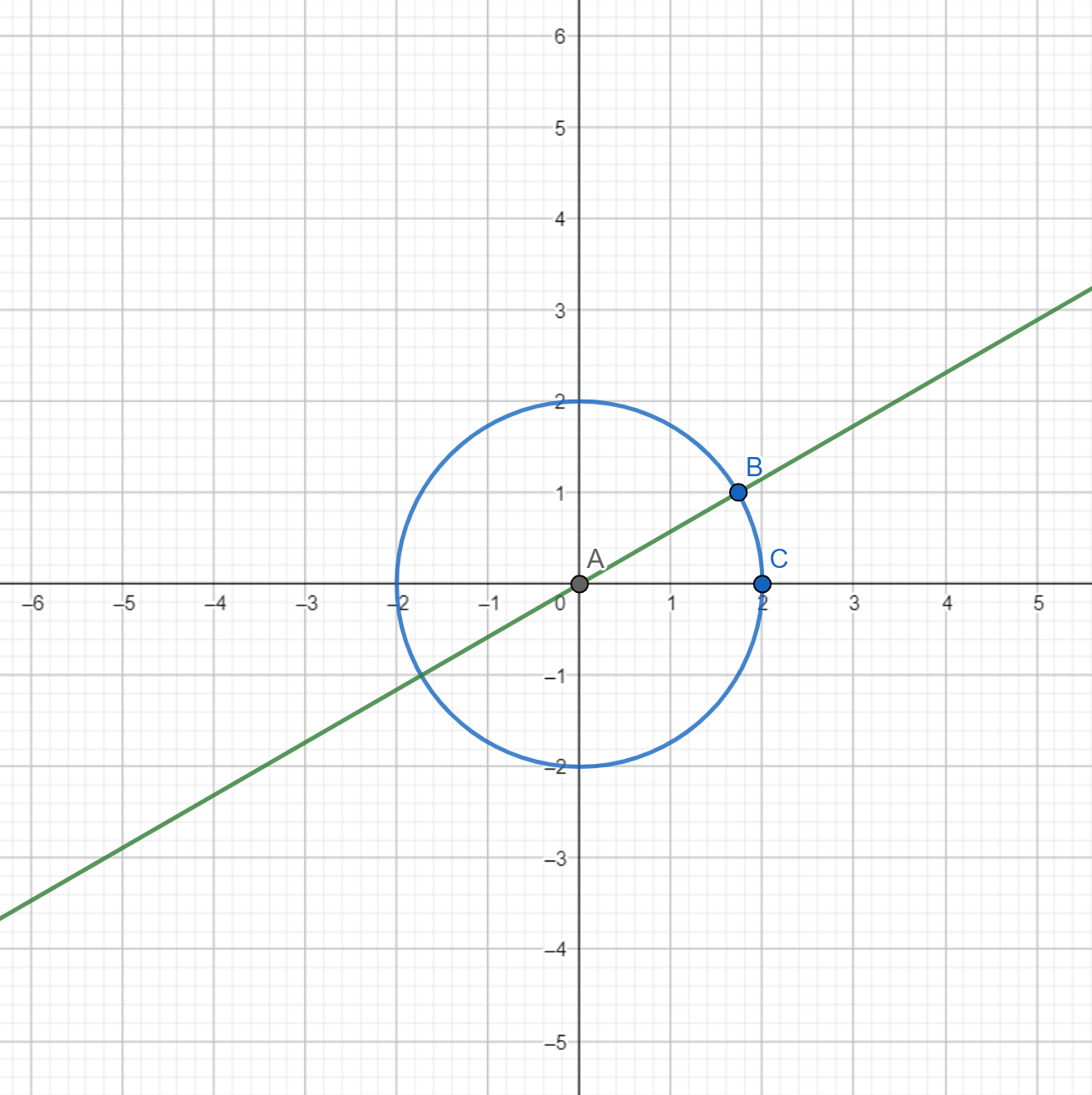
Question: 7 Find the area of the smaller part of the circle \small x^2+y^2=a^2 cut off by the line
\small x=\frac{a}{\sqrt{2}}

Answer:

1646972273424
we need to find the area of smaller part of the circle
Now,
Area of ABCD = 2 X Area of ABC
Area of ABC = \int_{\frac{a}{\sqrt2}}^{a} ydx= \int_{\frac{a}{\sqrt2}}^{a} \sqrt{a^2-x^2}dx= \left [ \frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2}\sin^{-1}\frac{x}{a}\right ]^{a}_\frac{a}{\sqrt2}\\ \\
=\left [ \frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}\sin^{-1}\frac{a}{a}- \frac{a}{2\sqrt2}\sqrt{a^2-(\frac{a}{\sqrt2})^2}-\frac{a^2}{2}\sin^{-1}\frac{a}{a\sqrt2}\right ]
=\left [ \frac{a}{2}\sqrt{0}+\frac{a^2}{2}\sin^{-1}1- \frac{a}{2\sqrt2}\sqrt{\frac{a^2}{2}}-\frac{a^2}{2}\sin^{-1}\frac{1}{\sqrt2}\right ]
=\left [ 0+\frac{a^2}{2}\frac{\pi}{2}- \frac{a^2}{4}-\frac{a^2}{2}\frac{\pi}{4}\right ]
=\frac{a^2}{4}\left ( \frac{\pi}{2}-1 \right )
Area of ABCD = 2 X Area of ABC
=2\times\frac{a^2}{4}\left ( \frac{\pi}{2}-1 \right )= \frac{a^2}{2}\left ( \frac{\pi}{2}-1 \right )
Therefore, the area of the smaller part of the circle is \frac{a^2}{2}\left ( \frac{\pi}{2}-1 \right )

Question:8 The area between \small x=y^2 and \small x=4 is divided into two equal parts by the line \small x=a , find the value of \small a .

Answer:

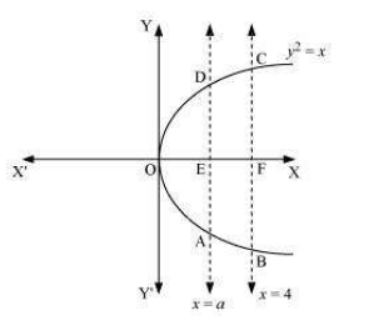1646972308309 we can clearly see that given area is symmetrical about x - axis
It is given that
Area of OED = Area of EFCD
Area of OED = \int_{0}^{a}ydx = \int_{0}^{a}\sqrt xdx = \left [ \frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]_0^{a}= \frac{a^{\frac{3}{2}}}{\frac{3}{2}} = \frac{2a^{\frac{3}{2}}}{3}
Area of EFCD = \int_{a}^{4}ydx = \int_{a}^{4}\sqrt xdx = \left [ \frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]_a^{4}= \frac{4^{\frac{3}{2}}-a^\frac{3}{2}}{\frac{3}{2}} = \frac{2(8-a^\frac{3}{2})}{3}=\frac{2(8-a^\frac{3}{2})}{3}
Area of OED = Area of EFCD
\frac{2a^{\frac{3}{2}}}{3}= \frac{2(8-a^{\frac{3}{2}})}{3}\\ \\ 2a^\frac{3}{2} = 8\\ a^\frac{3}{2} = 4\\ a = (4)^\frac{2}{3}
Therefore, the value of a is a = (4)^\frac{2}{3}

Question:9 Find the area of the region bounded by the parabola \small y=x^2 and \small y=|x| .

Answer:

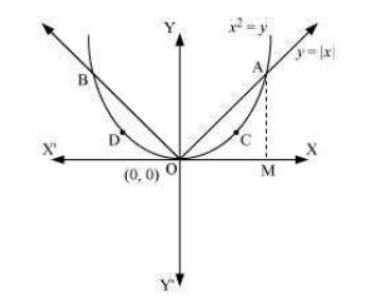1646972345767 We can clearly see that given area is symmetrical about y-axis
Therefore,
Area of OCAO = Area of OBDO
Point of intersection of y=x^2 \ and \ y = |x| is (1 , 1) and (-1 , 1)
Now,
Area od OCAO = Area OAM - Area of OCMO
Area of OAM = \frac{1}{2}.OM.AM = \frac{1}{2}.1.1 = \frac{1}{2}
Area of OCMO = \int_{0}^{1}ydx= \int_{0}^{1}x^2dx= \left [ \frac{x^3}{3} \right ]_{0}^{1}= \frac{1}{3}
Therefore,
Area od OCAO =\frac{1}{2}- \frac{1}{3}= \frac{1}{6}
Now,
Area of the region bounded by the parabola \small y=x^2 and \small y=|x| is = 2 X Area od OCAO =2\times \frac{1}{6} = \frac{1}{3} Units

Question: 10 Find the area bounded by the curve \small x^2=4y and the line \small x=4y-2 .

Answer:

1646972388198 Points of intersections of y = x^2 \ and \ x = 4y-2 is
A\left ( -1,\frac{1}{4} \right ) \ and \ B(2,1)
Now,
Area of OBAO = Area of OBCO + Area of OCAO
Area of OBCO = Area of OMBCO- Area of OMBO

Area of OMBCO = \int_{0}^{2}ydx = \int_{0}^{2}\frac{x+2}{4}dx = \left [ \frac{x^2}{8} \right ]_{0}^{2}+\left [ \frac{x}{2} \right ]_{0}^{2}= \frac{4}{8}+\frac{2}{2}=\frac{3}{2}

Area of OMBO = \int_{0}^{2}ydx = \int_{0}^{2}\frac{x^2}{4}dx = \left [ \frac{x^3}{12} \right ]_{0}^{2}= \frac{8}{12}= \frac{2}{3}

Area of OBCO = Area of OMBCO- Area of OMBO
= \frac{3}{2}-\frac{2}{3}= \frac{5}{6}
Similarly,
Area of OCAO = Area of OCALO - Area of OALO

Area of OCALO = \int_{-1}^{0}ydx = \int_{-1}^{0}\frac{x+2}{4}dx = \left [ \frac{x^2}{8} \right ]_{-1}^{0}+\left [ \frac{x}{2} \right ]_{-1}^{0}=- \frac{1}{8}-\frac{(-1)}{2}=-\frac{1}{8}+\frac{1}{2}=\frac{3}{8}

Area of OALO = \int_{-1}^{0}ydx = \int_{-1}^{0}\frac{x^2}{4}dx = \left [ \frac{x^3}{12} \right ]_{-1}^{0}= -\frac{(-1)}{12}= \frac{1}{12}

Area of OCAO = Area of OCALO - Area of OALO
=\frac{3}{8}- \frac{1}{12}= \frac{9-2}{24}= \frac{7}{24}
Now,
Area of OBAO = Area of OBCO + Area of OCAO
=\frac{5}{6}+ \frac{7}{24}= \frac{20+7}{24}= \frac{27}{24} = \frac{9}{8}

Therefore, area bounded by the curve \small x^2=4y and the line \small x=4y-2 is \frac{9}{8} \ units

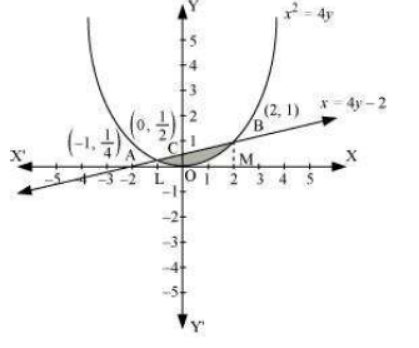
Question: 11 Find the area of the region bounded by the curve \small y^2=4x and the line \small x=3 .

Answer:
The combined figure of the curve y^2=4x and x=3
15947265752881594726573011
The required are is OABCO, and it is symmetrical about the horizontal axis.
Therefore, Area of OABCO = 2 \times Area of OAB
\\=2[\int_{0}^{3}ydx]\\ =2\int^3_02\sqrt{x}dx\\ =4[\frac{x^{3/2}}{3/2}]^3_0\\ =8\sqrt{3}
therefore the required area is 8\sqrt{3} units.

Question: 12 Choose the correct answer in the following

Area lying in the first quadrant and bounded by the circle \small x^2+y^2=4 and the lines \small x=0 and \small x=2 is

\small (A)\hspace{1mm}\pi \small (B)\hspace{1mm}\frac{\pi }{2} \small (C)\hspace{1mm}\frac{\pi }{3} \small (D)\hspace{1mm}\frac{\pi }{4}

Answer:

The correct answer is A
The area bounded by circle C(0,0,4) and the line x=2 is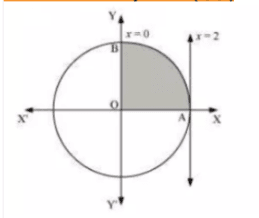
15947268860371594726883361
The required area = area of OAB
\int^2_0ydx = \int^2_0\sqrt{4-x^2}dx
\\=[\frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}\sin^{-1}\frac{x}{2}]^2_0\\ =2(\pi/2)\\ =\pi

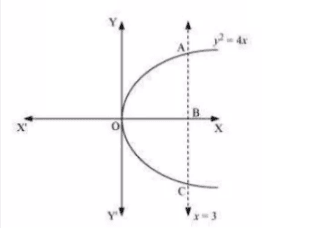
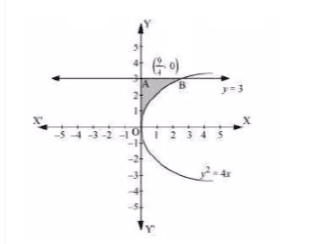
Question: 13 Choose the correct answer in the following.

Area of the region bounded by the curve \small y^2=4x , \small y -axis and the line \small y=3 is

(A) \small 2 (B) \small \frac{9}{4} (C) \small \frac{9}{3} (D) \small \frac{9}{2}

Answer:

The area bounded by the curve y^2=4x and y =3

15947271505371594727147434
the required area = OAB =
\\\int ^3_0xdy\\ =\int ^3_0\frac{y^2}{4}dy\\ =\frac{1}{4}.[\frac{y^3}{3}]^3_0\\ =\frac{9}{4}


NCERT application of integrals class 12 solutions Exercise: 8.2

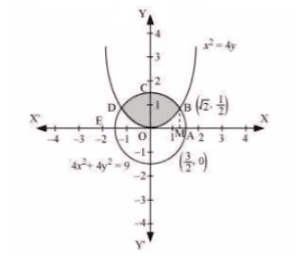
Question: 1 Find the area of the circle \small 4x^2+4y^2=9 which is interior to the parabola \small x^2=4y .

Answer:

The area bounded by the circle \small 4x^2+4y^2=9 and the parabola \small x^2=4y .
15947278183451594727815379
By solving the equation we get the intersecting point D(-\sqrt{2},\frac{1}{2}) and B(\sqrt{2},\frac{1}{2})
So, the required area (OBCDO)=2 times the area of (OBCO)
Draw a normal on the x-axis (M = \sqrt{2},0 )


Thus the area of OBCO = Area of OMBCO - Area of OMBO

\\\int_{0}^{\sqrt{2}}\sqrt{\frac{(9-4x^2)}{4}}dx-\int_{0}^{\sqrt{2}}{\frac{x^2}{4}}dx\\ =\frac{1}{2}\int_{0}^{\sqrt{2}}\sqrt{9-4x^2}-\frac{1}{4}\int_{0}^{\sqrt{2}}x^2dx\\ =\frac{1}{4}[x\sqrt{9-4x^2}+\frac{9}{2}\sin^{-1}\frac{2x}{3}]_0^{\sqrt{2}}-\frac{1}{4}[\frac{x^3}{3}]_0^{\sqrt{2}}\\ =\frac{1}{4}[\sqrt{2}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}]-\frac{1}{12}(\sqrt{2})^3\\ =\frac{\sqrt{2}}{12}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\\ =\frac{1}{2}(\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3})
S0, total area =
\\=2\times \frac{1}{2}(\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3})\\ =\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3}

Question:2 Find the area bounded by curves \small (x-1)^2+y^2=1 and \small x^2+y^2=1 .

Answer:

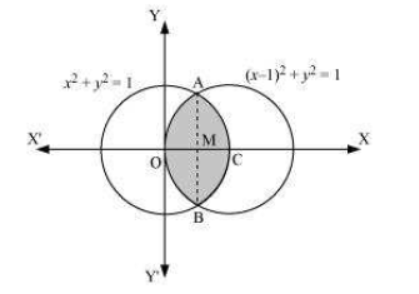1646972457138 Given curves are \small (x-1)^2+y^2=1 and \small x^2+y^2=1

Point of intersection of these two curves are

A = \left ( \frac{1}{2},\frac{\sqrt3}{2} \right ) and B = \left ( \frac{1}{2},-\frac{\sqrt3}{2} \right )

We can clearly see that the required area is symmetrical about the x-axis

Therefore,

Area of OBCAO = 2 \times Area of OCAO

Now, join AB such that it intersects the x-axis at M and AM is perpendicular to OC

Coordinates of M = \left ( \frac{1}{2},0 \right )

Now,

Area OCAO = Area OMAO + Area CMAC

=\left [ \int_{0}^{\frac{1}{2}}\sqrt{1-(x-1)^2}dx +\int_{\frac{1}{2}}^{1}\sqrt{1-x^2}dx \right ]
=\left [ \frac{x-1}{2}\sqrt{1-(x-1)^2}+\frac{1}{2}\sin^{-1}(x-1) \right ]_{0}^{\frac{1}{2}}+\left [ \frac{x}{2}+\frac{1}{2}\sin^{-1}x \right ]_{\frac{1}{2}}^{1}

=\left [- \frac{1}{4}\sqrt{1-(-\frac{1}{2})^2}+\frac{1}{2}\sin^{-1}(\frac{1}{2}-1)-0-\frac{1}{2}\sin^{-1}(-1) \right ]+\left [ 0+\frac{1}{2}\sin^{-1}(1)- \frac{1}{4}\sqrt{1-\left ( \frac{1}{2} \right )^2}-\frac{1}{2}\sin^{-1}\left ( \frac{1}{2} \right )\right ]
=\left [ -\frac{\sqrt3}{8}+\frac{1}{2}\left ( -\frac{\pi}{6} \right )-\frac{1}{2}\left ( -\frac{\pi}{2} \right ) \right ]+\left [ \frac{1}{2}\left ( \frac{\pi}{2} \right ) -\frac{\sqrt3}{8}-\frac{1}{2}\left ( \frac{\pi}{6} \right )\right ]
= \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]+\left [ \frac{\pi}{6}-\frac{\sqrt3}{8} \right ]
=2 \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]
Now,
Area of OBCAO = 2 \times Area of OCAO

=2\times 2 \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]
=\frac{2\pi}{3}-\frac{\sqrt3}{2}

Therefore, the answer is \frac{2\pi}{3}-\frac{\sqrt3}{2}

Question: 3 Find the area of the region bounded by the curves \small y=x^2+2,y=x,x=0 and \small x=3 .

Answer:

The area of the region bounded by the curves,

\small y=x^2+2,y=x,x=0 and \small x=3 is represented by the shaded area OCBAO as

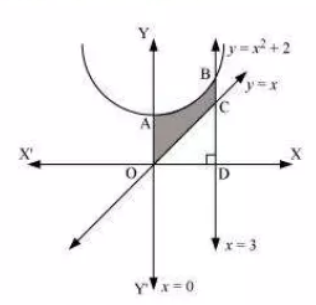
1646972497382

Then, Area OCBAO will be = Area of ODBAO - Area of ODCO

which is equal to

\int_0^3(x^2+2)dx - \int_0^3x dx

= \left ( \frac{x^3}{3}+2x \right )_0^3 -\left ( \frac{x^3}{2} \right )_0^3

= \left [ 9+6 \right ] - \left [ \frac{9}{2} \right ] = 15-\frac{9}{2} = \frac{21}{2}units.

Question: 4 Using integration find the area of region bounded by the triangle whose vertices are \small (-1,0),(1,3) and \small (3,2) .

Answer:

So, we draw BL and CM perpendicular to x-axis.

Then it can be observed in the following figure that,

Area(\triangle ACB) = Area (ALBA)+Area(BLMCB) - Area (AMCA)

We have the graph as follows:

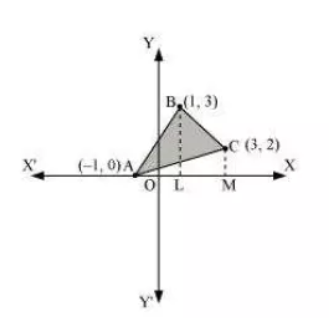
1646972546438

Equation of the line segment AB is:

y-0 = \frac{3-0}{1+1}(x+1) or y = \frac{3}{2}(x+1)

Therefore we have Area of ALBA

=\int_{-1}^1 \frac{3}{2}(x+1)dx =\frac{3}{2}\left [ \frac{x^2}{2}+x \right ]_{-1}^1

=\frac{3}{2}\left [ \frac{1}{2}+1-\frac{1}{2}+1 \right ] =3units.

So, the equation of line segment BC is

y-3 = \frac{2-3}{3-1}(x-1) or y= \frac{1}{2}(-x+7)

Therefore the area of BLMCB will be,

=\int_1^3 \frac{1}{2}(-x+7)dx =\frac{1}{2}\left [ -\frac{x^2}{2}+7x \right ]_1^3

= \frac{1}{2}\left [ -\frac{9}{2}+21+\frac{1}{2}-7 \right ] =5units.

Equation of the line segment AC is,

y-0 = \frac{2-0}{3+1}(x+1) or y = \frac{1}{2}(x+1)

Therefore the area of AMCA will be,

=\frac{1}{2}\int_{-1}^3 (x+1)dx =\frac{1}{2}\left [ \frac{x^2}{2}+x \right ]_{-1}^3

=\frac{1}{2}\left ( \frac{9}{2}+3-\frac{1}{2}+1 \right ) = 4units.

Therefore, from equations (1), we get

The area of the triangle \triangle ABC =3+5-4 =4units.

Question:5 Using integration find the area of the triangular region whose sides have the equations \small y=2x+1,y=3x+1 and \small x=4 .

Answer:

The equations of sides of the triangle are y=2x+1, y =3x+1,\ and\ x=4 .

ON solving these equations, we will get the vertices of the triangle as A(0,1),B(4,13),\ and\ C(4,9)

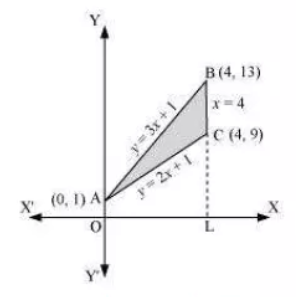
1646972586017

Thus it can be seen that,

Area (\triangle ACB) = Area (OLBAO) -Area (OLCAO)

= \int_0^4 (3x+1)dx -\int_0^4(2x+1)dx

= \left [ \frac{3x^2}{2}+x \right ]_0^4 - \left [ \frac{2x^2}{2}+x \right ]_0^4

=(24+4) - (16+4) = 28-20 =8units.

Question:6 Choose the correct answer.

Smaller area enclosed by the circle \small x^2+y^2=4 and the line \small x+y=2 is

(A) \small 2(\pi -2) (B) \small \pi -2 (C) \small 2\pi -1 (D) \small 2(\pi +2)

Answer:

So, the smaller area enclosed by the circle, x^2+y^2 =4 , and the line, x+y =2 , is represented by the shaded area ACBA as

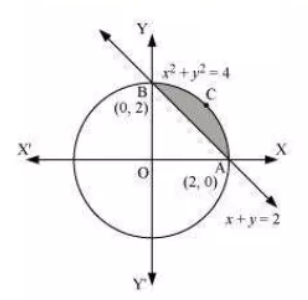
1646972621266

Thus it can be observed that,

Area of ACBA = Area OACBO - Area of (\triangle OAB)

=\int_0^2 \sqrt{4-x^2} dx -\int_0^2 (2-x)dx

= \left ( \frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}\sin^{-1}{\frac{x}{2}} \right )_0^2 - \left ( 2x -\frac{x^2}{2} \right )_0^2

= \left [ 2.\frac{\pi}{2} \right ] -[4-2]

= (\pi -2) units.

Thus, the correct answer is B.

Question:7 Choose the correct answer.

Area lying between the curves \small y^2=4x and \small y=2x is

(A) \small \frac{2}{3} (B) \small \frac{1}{3} (C) \small \frac{1}{4} (D) \small \frac{3}{4}

Answer:

The area lying between the curve, \small y^2=4x and \small y=2x is represented by the shaded area OBAO as

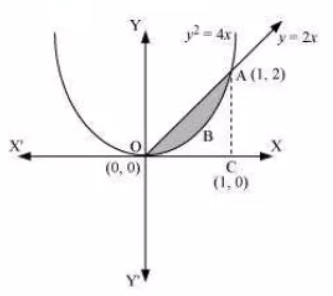
1646972657802

The points of intersection of these curves are O(0,0) and A (1,2) .

So, we draw AC perpendicular to x-axis such that the coordinates of C are (1,0).

Therefore the Area OBAO = Area(\triangle OCA) -Area (OCABO)

=2\left [ \frac{x^2}{2} \right ]_0^1 - 2\left [ \frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]_0^1

=\left | 1-\frac{4}{3} \right | = \left | -\frac{1}{3} \right | = \frac{1}{3} units.

Thus the correct answer is B.


NCERT application of integrals class 12 solutions Miscellaneous: Exercise

Question:1 Find the area under the given curves and given lines:

(i) \small y=x^2,x=1,x=2 and \small x -axis

Answer:

The area bounded by the curve \small y=x^2,x=1,x=2 and \small x -axis
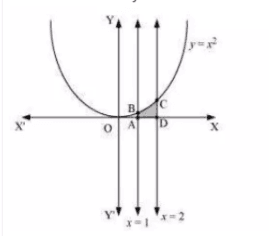
15947281267411594728124007
The area of the required region = area of ABCD
\\=\int_{1}^{2}ydx\\ =\int_{1}^{2}x^2dx\\ =[\frac{x^3}{3}]_1^2\\ =\frac{7}{3}
Hence the area of shaded region is 7/3 units

Question:1 Find the area under the given curves and given lines:

(ii) \small y=x^4,x=1,x=5 and \small x -axis

Answer:

The area bounded by the curev \small y=x^4,x=1,x=5 and \small x -axis

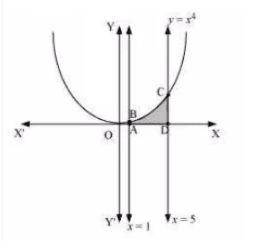
15947282868341594728284206
The area of the required region = area of ABCD
\\=\int_{1}^{5}ydx\\ =\int_{1}^{2}x^4dx\\ =[\frac{x^5}{5}]_1^2\\ =625-\frac{1}{5}\\ =624.8
Hence the area of the shaded region is 624.8 units

Question:2 Find the area between the curves \small y=x and \small y=x^2 .

Answer:

the area between the curves \small y=x and \small y=x^2 .
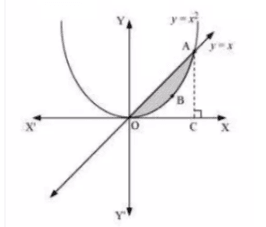
AOI graph1594728523616
The curves intersect at A(1,1)
Draw a normal to AC to OC(x-axis)
therefore, the required area (OBAO)= area of (OCAO) - area of (OCABO)
\\=\int_{0}^{1}xdx-\int_{0}^{1}x^2dx\\ =[\frac{x^2}{2}]_0^1-[\frac{x^3}{3}]_0^1\\ =1/2-1/3\\ =\frac{1}{6}
Thus the area of shaded region is 1/6 units

Question:3 Find the area of the region lying in the first quadrant and bounded by \small y=4x^2,x=0,y=1 and \small y=4 .

Answer:

the area of the region lying in the first quadrant and bounded by \small y=4x^2,x=0,y=1 and \small y=4 .

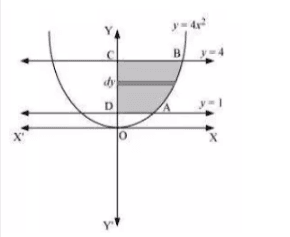
15947286788651594728676557
The required area (ABCD) =
\\=\int_{1}^{4}xdy\\ =\int_{1}^{4}\frac{\sqrt{y}}{2}dy\\ =\frac{1}{2}.\frac{2}{3}[y^{3/2}]_1^4\\ =\frac{1}{3}[8-1]\\ =\frac{7}{3}
The area of the shaded region is 7/3 units

Question:4 Sketch the graph of \small y=|x+3| and evaluate \small \int_{-6}^{0}|x+3|dx.

Answer:

y=|x+3|

the given modulus function can be written as

x+3>0

x>-3

for x>-3

y=|x+3|=x+3

x+3<0

x<-3

For x<-3

y=|x+3|=-(x+3)

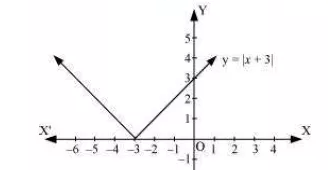
1646972694635

Integral to be evaluated is

\\\int_{-6}^{0}|x+3|dx\\ =\int_{-6}^{-3}(-x-3)dx+\int_{-3}^{0}(x+3)dx\\ =[-\frac{x^{2}}{2}-3x]_{-6}^{-3}+[\frac{x^{2}}{2}+3x]_{-3}^{0}\\ =(-\frac{9}{2}+9)-(-18+18)+0-(\frac{9}{2}-9)\\ =9

Question:5 Find the area bounded by the curve \small y=\sin x between \small x=0 and \small x=2\pi .

Answer:

The graph of y=sinx is as follows

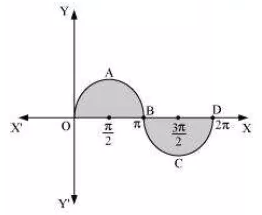
1646972720677

We need to find the area of the shaded region

ar(OAB)+ar(BCD)

=2ar(OAB)

\\=2\times \int_{0}^{\pi }sinxdx\\ =2\times [-cosx]_{0}^{\pi }\\ =2\times [-(-1)-(-1)]\\ =4

The bounded area is 4 units.

Question:6 Find the area enclosed between the parabola \small y^2=4ax and the line \small y=mx .

Answer:

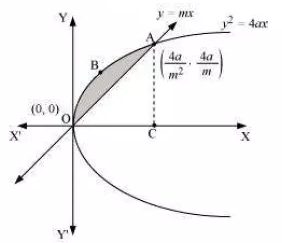
1646972749429

We have to find the area of the shaded region OBA

The curves y=mx and y 2 =4ax intersect at the following points

\left ( 0,0 \right )and\left ( \frac{4a}{m^{2}},\frac{4a}{m} \right )

\\y^{2}=4ax\\ \Rightarrow y=2\sqrt{ax}

The required area is

\\\int_{0}^{\frac{4a}{m^{2}}}(2\sqrt{ax}-mx)\\ =2\sqrt{a}[\frac{2x^{\frac{3}{2}}}{3}]_{0}^{\frac{4a}{m^{2}}}-m[\frac{x^{2}}{2}]_{0}^{\frac{4a}{m^{2}}}\\ =\frac{32a^{2}}{3m^{3}}-\frac{8a^{2}}{m^{3}}\\ =\frac{8a^{2}}{3m^{3}}units

Question:7 Find the area enclosed by the parabola \small 4y=3x^2 and the line \small 2y=3x+12 .

Answer:

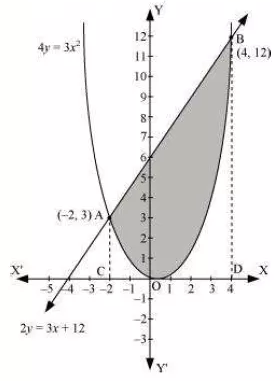
1646972775838

We have to find the area of the shaded region COB

\\2y=3x+12\\ \Rightarrow y=\frac{3}{2}x+6\\ 4y=3x^{2}\\ \Rightarrow y=\frac{3x^{2}}{4}

The two curves intersect at points (2,3) and (4,12)

Required area is

\\\int_{-2}^{4}(\frac{3}{2}x+6-\frac{3x^{2}}{4})dx\\ =[\frac{3x^{2}}{4}+6x-\frac{x^{3}}{4}]{_{-2}}^{4}\\ =[12+24-16]-[3-12+2]\\ =20-(-7)\\ =27\ units

Question:8 Find the area of the smaller region bounded by the ellipse \small \frac{x^2}{9}+\frac{y^2}{4}=1 and the line \small \frac{x}{3}+\frac{y}{2}=1 .

Answer:

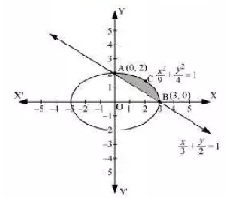
1646972803949

We have to find the area of the shaded region

The given ellipse and the given line intersect at following points

\left ( 0,2 \right )and \left ( 3,0 \right )

\\\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\\ y=\frac{2}{3}\sqrt{9-x^{2}}

Since the shaded region lies above x axis we take y to be positive

\\\frac{x}{3}+\frac{y}{2}=1\\ y=\frac{2}{3}(3-x)

The required area is

\\\frac{2}{3}\int_{0}^{3}\left ( \sqrt{9-x^{2}}-(3-x) \right )dx\\ =\frac{2}{3}[\frac{x}{2}(\sqrt{9-x^{2}})+\frac{9}{2}sin^{-1}\frac{x}{3}-3x+\frac{x^{2}}{2}]_{0}^{3}\\ =\frac{2}{3}\left ( \left [ \frac{9}{2}\times \frac{\pi }{2}-9+\frac{9}{2} \right ]-0 \right )\\ =\frac{2}{3}(\frac{9\pi }{4}-\frac{9}{2})\\ =\frac{3}{2}(\pi -2)units

Question:9 Find the area of the smaller region bounded by the ellipse \small \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 and the line \small \frac{x}{a}+\frac{y}{b}=1 .

Answer:


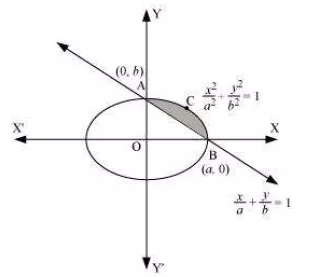
1646972828912

The area of the shaded region ACB is to be found

The given ellipse and the line intersect at following points

\left ( 0,b \right )and\left ( a,0 \right )

\\\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\\ \Rightarrow y=\frac{b}{a}\sqrt{a^{2}-x^{2}}

Y will always be positive since the shaded region lies above x axis

\\\frac{x}{a}+\frac{y}{b}=1\\ \Rightarrow y=\frac{b}{a}(a-x)

The required area is

\\\frac{b}{a}\int_{0}^{a}(\sqrt{a^{2}-x^{2}}-(a-x))dx\\ =\frac{b}{a}[\frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}sin^{-1}\frac{x}{a}-ax+\frac{x^{2}}{2}]_{0}^{a}\\ =\frac{b}{a}[(\frac{a^{2}}{2}\times \frac{\pi }{2}-a^{2}+\frac{a^{2}}{2})]\\ =\frac{b}{a}(\frac{\pi a^{2}}{4}-\frac{a^{2}}{2})\\ =\frac{ab}{4}(\pi -2)units


Question:10 Find the area of the region enclosed by the parabola \small x^2=y, the line \small y=x+2 and the \small x -axis.

Answer:

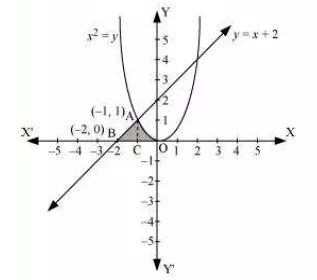
1646972855917

We have to find the area of the shaded region BAOB

O is(0,0)

The line and the parabola intersect in the second quadrant at (-1,1)

The line y=x+2 intersects the x axis at (-2,0)

\\ar(BAOB)=ar(BAC)+ar(ACO)\\ =\int_{-2}^{-1}(x+2)dx+\int_{-1}^{0}(x^{2})dx\\ =[\frac{x^{2}}{2}+2x]_{-2}^{-1}+[\frac{x^{3}}{3}]_{-1}^{0}\\ =(\frac{1}{2}-2)-(2-4)+0-(-\frac{1}{3})\\ =\frac{5}{6}\ units

The area of the region enclosed by the parabola \small x^2=y, the line \small y=x+2 and the \small x -axis is 5/6 units.

Question:11 Using the method of integration find the area bounded by the curve \small |x|+|y|=1.

[ Hint: The required region is bounded by lines \small x+y=1,x-y=1,-x+y=1 and \small -x-y=1 ]

Answer:

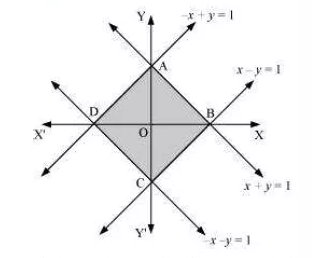
1646972880742

We need to find the area of the shaded region ABCD

ar(ABCD)=4ar(AOB)

Coordinates of points A and B are (0,1) and (1,0)

Equation of line through A and B is y=1-x

\\ar(AOB)=\int_{0}^{1}(1-x)dx\\ =[x-\frac{x^{2}}{2}]_{0}^{1}\\ =(1-\frac{1}{2})-0 \\=\frac{1}{2}\ units\\ ar(ABCD)=4ar(AOB)\\ =4\times \frac{1}{2}\\ =2\ units

The area bounded by the curve \small |x|+|y|=1 is 2 units.

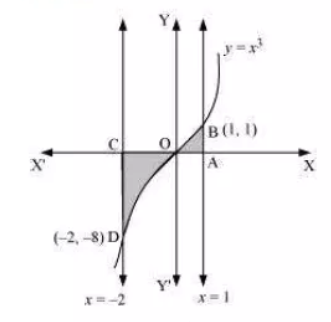
Question:12 Find the area bounded by curves \small \left \{ (x,y);y\geq x^2\hspace{1mm} and \hspace{1mm}y=|x| \right \} .

Answer:

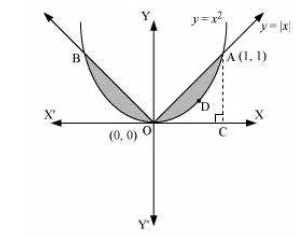
1646972905611

We have to find the area of the shaded region

In the first quadrant

y=|x|=x

Area of the shaded region=2ar(OADO)

\\=2\int_{0}^{1}(x-x^{2})dx\\ =2[\frac{x^{2}}{2}-\frac{x^{3}}{3}]{_{0}}^{1} \\=2(\frac{1}{2}-\frac{1}{3})-0\\ =1-\frac{2}{3}\\ =\frac{1}{3}\ units

The area bounded by the curves is 1/3 units.

Question:13 Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are \small A(2,0),B(4,5)\hspace{1mm}and\hspace{1mm}C(6,3).

Answer:

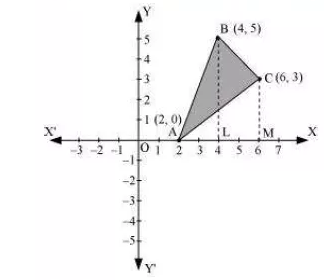
1646972934221

Equation of line joining A and B is

\\\frac{y-0}{x-2}=\frac{5-0}{4-2}\\ y=\frac{5x}{2}-5

Equation of line joining B and C is

\\\frac{y-5}{x-4}=\frac{5-3}{4-6}\\ y=9-x

Equation of line joining A and C is

\\\frac{y-0}{x-2}=\frac{3-0}{6-2}\\ y=\frac{3x}{4}-\frac{3}{2}

ar(ABC)=ar(ABL)+ar(LBCM)-ar(ACM)

\\ar(ABL)=\int_{2}^{4}(\frac{5x}{2}-5)dx\\ =[\frac{5x^{2}}{4}-5x]_{2}^{4}\\ =(20-20)-(5-10)\\ =5\ units

\\ar(LBCM)=\int_{4}^{6}(9-x)dx\\ =[9x-\frac{x^{2}}{2}]_{4}^{6}\\ =(54-18)-(36-8)\\ =8\ units

\\ar(ACM)=\int_{2}^{6}(\frac{3x}{4}-\frac{3}{2})dx\\ =[\frac{3x^{2}}{8}-\frac{3x}{2}]_{2}^{6}\\ =(\frac{27}{2}-9)-(\frac{3}{2}-3)\\ =6\ units

ar(ABC)=8+5-6=7

Therefore the area of the triangle ABC is 7 units.

Question:14 Using the method of integration find the area of the region bounded by lines:
\small 2x+y=4,3x-2y=6\hspace{1mm}and\hspace{1mm}x-3y+5=0.

Answer:

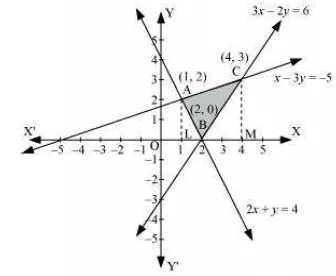
1646972962041

We have to find the area of the shaded region ABC

ar(ABC)=ar(ACLM)-ar(ALB)-ar(BMC)

The lines intersect at points (1,2), (4,3) and (2,0)

\\x-3y=-5\\ y=\frac{x}{3}+\frac{5}{3}

\\ar(ACLM)=\int_{1}^{4}(\frac{x}{3}+\frac{5}{3})dx\\ =[\frac{x^{2}}{6}+\frac{5x}{3}]_{1}^{4}\\ =(\frac{4^{2}}{6}+\frac{5\times 4}{3})-(\frac{1}{6}+\frac{5}{3})\\ =\frac{15}{2}\ units

\\2x+y=4\\ y=4-2x

\\ar(ALB)=\int_{1}^{2}(4-2x)dx\\ =[4x-x^{2}]_{1}^{2}\\ =(8-4)-(4-1)\\ =1\ unit

\\3x-2y=6\\ y=\frac{3x}{2}-3

\\ar(BMC)=\int_{2}^{4}(\frac{3x}{2}-3)dx\\ =[\frac{3x^{2}}{4}-3x]_{2}^{4}\\ =(12-12)-(3-6)\\ =3\ units

\\ ar(ABC)=\frac{15}{2}-1-3\\ =\frac{7}{2}\ units

Area of the region bounded by the lines is 3.5 units

Question:15 Find the area of the region \small \left \{ (x,y);y^2\leq 4x,4x^2+4y^2\leq 9 \right \} .

Answer:

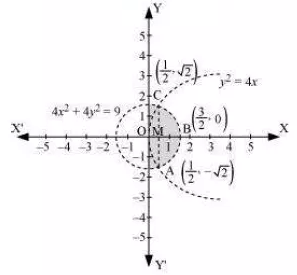
1646972988754

We have to find the area of the shaded region OCBAO

Ar(OCBAO)=2ar(OCBO)

For the fist quadrant

\\4x^{2}+4y^{2}=9\\ y=\sqrt{\frac{9}{4}-x^{2}}

\\y^{2}=4x\\ y=2\sqrt{x}

In the first quadrant, the curves intersect at a point \left ( \frac{1}{2},\sqrt{2} \right )

Area of the unshaded region in the first quadrant is

\\\int_{0}^{\frac{1}{2}}\left ( \sqrt{\frac{9}{4}-x^{2}} -2\sqrt{x}\right )dx\\ =[\frac{x}{2}\sqrt{\frac{9}{4}-x^{2}}+\frac{9}{8}sin^{-1}\frac{2x}{3}]{_{0}}^{\frac{1}{2}}-4[\frac{x^{3/2}}{3}]_0^{1/2}\\ =\frac{\sqrt{2}}{4}+\frac{9}{8}sin^{-1}\frac{1}{3}-\frac{\sqrt{2}}{3}

The total area of the shaded region is-
= Area of half circle - area of the shaded region in the first quadrant

\\\frac{\pi }{2}\times (\frac{3}{2})^{2}-2\left ( \frac{\sqrt{2}}{4}-\frac{\sqrt{2}}{3}+\frac{9}{8}sin^{-1}\frac{1}{3}\right )\\ =\frac{9 }{8}\left ( \pi-2sin^{-1}\frac{1}{3} \right )+\frac{\sqrt{2}}{6}\ units

Question:16 Choose the correct answer.

Area bounded by the curve \small y=x^3 , the \small x -axis and the ordinates \small x=-2 and \small x=1 is

(A) \small -9 (B) \small \frac{-15}{4} (C) \small \frac{15}{4} (D) \small \frac{17}{4}

Answer:

1646973022742

Hence the required area

=\int_{-2}^1 ydx

=\int_{-2}^1 x^3dx = \left [ \frac{x^4}{4} \right ]_{-2}^1

= \left [ \frac{x^4}{4} \right ]^0_{-2} + \left [ \frac{x^4}{4} \right ]^1_{0}

= \left [ 0-\frac{(-2)^4}{4} \right ] + \left [ \frac{1}{4} - 0 \right ]

= -4+\frac{1}{4} = \frac{-15}{4}

Therefore the correct answer is B.

Question:17 Choose the correct answer.

T he area bounded by the curve \small y=x|x| , \small x -axis and the ordinates \small x=-1 and \small x=1 is given by

(A) \small 0 (B) \small \frac{1}{3} (C) \small \frac{2}{3} (D) \small \frac{4}{3}

[ Hint : y=x^2 if x> 0 and y=-x^2 if x<0 . ]

Answer:

The required area is

\\2\int_{0}^{1}x^{2}dx\\ =2\left [ \frac{x^{3}}{3} \right ]_{0}^{1}\\ =\frac{2}{3}\ units

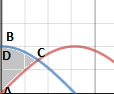
Question:18 Choose the correct answer.

The area of the circle \small x^2+y^2=16 exterior to the parabola \small y^2=6x is

(A) \small \frac{4}{3}(4\pi -\sqrt{3} ) (B) \small \frac{4}{3}(4\pi +\sqrt{3} ) (C) \small \frac{4}{3}(8\pi -\sqrt{3} ) (D) \small \frac{4}{3}(8\pi +\sqrt{3} )

Answer:

1646973081315

The area of the shaded region is to be found.

Required area =ar(DOC)+ar(DOA)

The region to the left of the y-axis is half of the circle with radius 4 units and centre origin.

Area of the shaded region to the left of y axis is ar(1) = \frac{\pi 4^{2}}{2}=8\pi\ units

For the region to the right of y-axis and above x axis

\\x^{2}+y^{2}=16\\ y=\sqrt{16-x^{2}}

\\y^{2}=6x\\ y=\sqrt{6x}

The parabola and the circle in the first quadrant intersect at point

\left ( 2,2\sqrt{3} \right )

Remaining area is 2ar(2) is

\\ar(2)=\int_{0}^{2}\left ( \sqrt{16-x^{2}}-\sqrt{6x} \right )dx\\ =[ \frac{x}{2}\sqrt{16-x^{2}}+\frac{16}{2}sin^{-1}(\frac{x}{4})-\frac{2\sqrt{6}}{3}x^{\frac{3}{2}} ]{_{0}}^{2}\\ =[\sqrt{12}+\frac{16}{2}\times \frac{\pi }{6}-\frac{4\sqrt{12}}{3}]\\ =\frac{4\pi }{3}-\frac{2\sqrt{3}}{3}

Total area of shaded region is

\\ar(1)+2ar(2)\\ =8\pi +\frac{8\pi}{3}-\frac{4\sqrt{3}}{3}\\ =\frac{4}{3}(8\pi -\sqrt{3})\ units

Question:19 Choose the correct answer The area bounded by the \small y -axis, \small y=\cos x and \small y=\sin x when \small 0\leq x\leq \frac{\pi }{2} is

(A) \small 2(\sqrt{2}-1) (B) \small \sqrt{2}-1 (C) \small \sqrt{2}+1 (D) \small \sqrt{2}

Answer:

Given : \small y=\cos x and \small y=\sin x

1646973113069


Area of shaded region = area of BCDB + are of ADCA

=\int_{\frac{1}{\sqrt{2}}}^{1}x dy +\int_{1}^{\frac{1}{\sqrt{2}}}x dy

=\int_{\frac{1}{\sqrt{2}}}^{1} cos^{-1} y .dy +\int_{1}^{\frac{1}{\sqrt{2}}} sin^{-1}x dy

=[y. cos^{-1}y - \sqrt{1-y^2}]_\frac{1}{\sqrt{2}}^1 + [x. sin^{-1}x + \sqrt{1-x^2}]_1^\frac{1}{\sqrt{2}}

= cos^{-1}(1)-\frac{1}{\sqrt{2}} cos^{-1}(\frac{1}{\sqrt{2}})+\sqrt{1-\frac{1}{2}}+\frac{1}{\sqrt{2}} sin^{-1}(\frac{1}{\sqrt{2}})+\sqrt{1-\frac{1}{2}}-1

=\frac{-\pi }{4\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{\pi }{4\sqrt{2}}+\frac{1}{\sqrt{2}}-1

=\frac{2}{\sqrt{2}} - 1

=\sqrt{2} - 1

Hence, the correct answer is B.

If you are looking for exercises solutions for chapter application of integrals class 12 then these are listed below.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

More about NCERT Solutions for Class 12 Maths chapter 8

Generally, one question (5 marks) is asked from this ch 8 maths class 12 in the 12th board final exam and you can score these 5 marks very easily with help of these NCERT solutions for class 12 maths chapter 8 application of integrals. In this chapter 8 class 12 maths, there are 2 exercises with 20 questions. In the NCERT class 12 maths ch 8 question answer, these questions are prepared and explained in a detailed manner using diagrams.

There are a total of 14 solved examples are given in the NCERT textbook to give a better understanding of the concepts related to the application of integrals class 12. Applications of integrals class 12 are indispensable for the Board exam. At the end of the chapter, 19 questions are given in a miscellaneous exercise. In the NCERT solutions for class 12 maths chapter 8 application of integrals article, you will get solutions to miscellaneous exercises too.

Application of integrals class 12 - Topics

8.1 Introduction

8.2 Area under Simple Curves

8.2.1 The area of the region bounded by a curve and a line

8.3 Area between Two Curves

Also read,

SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Let's understand these topics with help of examples

  • How to find the area under simple curves- To find the area bounded by the curve 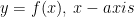y= f(x), \:x-axis and the ordinates x = a and x = b . Let assume that area under the curve as composed of large numbers of very thin vertical strips. Consider an arbitrary strip of width dx and height y ,then area of the elementary strip(dA) = ydx , where, y = f(x). This small area called the elementary area.

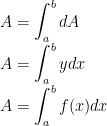
\\A=\int_{a}^{b}dA\\A=\int_{a}^{b}ydx\\A=\int_{a}^{b}f(x)dx

  • How to find the area of the region bounded by a curve and a line- In this subsection, we will find the area of the region bounded by a line and a circle, a line and an ellipse, a line and a parabola. Equations of the above-said curves will be in their standard forms only.

NCERT solutions for class 12 maths - Chapter wise

chapter 1NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
chapter 2NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
chapter 3NCERT solutions for class 12 maths chapter 3 Matrices
chapter 4NCERT solutions for class 12 maths chapter 4 Determinants
chapter 5NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
chapter 6NCERT solutions for class 12 maths chapter 6 Application of Derivatives
chapter 7NCERT solutions for class 12 maths chapter 7 Integrals
chapter 8NCERT solutions for class 12 maths chapter 8 Application of Integrals
chapter 9NCERT solutions for class 12 maths chapter 9 Differential Equations
chapter 10NCERT solutions for class 12 maths chapter 10 Vector Algebra
chapter 11NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
chapter 12NCERT solutions for class 12 maths chapter 12 Linear Programming
chapter 13NCERT solutions for class 12 maths chapter 13 Probability

Key Features of NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals

The application of integrals class 12 ncert solutions offers several key features, including

  1. Expertly crafted by knowledgeable subject specialists.

  2. Designed to enhance students' fundamental understanding of the applications of integrals.

  3. Clear and organized material.

  4. All questions are answered using informative diagrams.

  5. Supports students in completing their assignments and preparing for competitive exams.

NCERT solutions for class 12 subject wise

NCERT Solutions Class Wise

Benefits of NCERT solutions:

  • These NCERT maths chapter 8 class 12 solutions are very easy to understand as they are explained and are prepared in a detailed manner.
  • Scoring good marks in the 12th board exam is now a reality with the help of these solutions of NCERT for class 12 maths chapter 8 application of integrals.
  • NCERT solutions for Class 12 Maths Chapter 8 PDF download provides in-depth knowledge of the concepts as well as different ways to solve the problems.
  • NCERT maths chapter 8 class 12 solutions are prepared by experts who know how to answer to score well in the board exam.
  • You will also get some short tricks to check whether the answer is correct or not.

NCERT Books and NCERT Syllabus

Happy Reading !!!

Frequently Asked Question (FAQs)

1. What is the weightage of the chapter Application of integrals for CBSE board exam ?

Generally, one question of 5 marks is asked from this chapter in the 12th board final exam but if you want to obtain the full 5 five marks that demands practice, good strategy, and command of concepts, and therefore NCERT textbooks, NCERT syllabus becomes very important. it is advised for students to precisely go through the basics of class 12 maths chapter 8 question answer to score good marks. 

2. How does the NCERT solutions are helpful in the CBSE board exam ?

Only knowing the answer is not enough to score good marks in the exam. One should know how to write the answer to board exam in order to get good marks. NCERT solutions are provided by experts who knows how best to write the answer in the board exam in order to get good marks. Practice class 12 maths chapter 8 question answer to command the concepts.

3. What are the strategies for achieving maximum marks in class 12 math chapter 8 application of integrals ncert solutions?

The NCERT Solutions for the application of integration class 12 at Careers360 are created by a team of experts through extensive research on each concept. The solutions are presented in a thorough and comprehensive manner, enabling students to perform well on class exams and board exams. Additionally, the solutions aid students in completing their assignments efficiently and on time. Interested students can download the application of integrals class 12 pdf.

4. Where can I find the complete solutions of NCERT for class 12 maths ?

Here you will get the detailed and comprehensive NCERT Solutions for class 12 maths by clicking on the link. if  you want to study other material like NCERT Syllabus, NCERT Notes, NCERT Exercise Solutions, etc then you can browse the careers360 official website. 

5. What are the important topics in chapter Application of integrals ?

Some applications of integrals like finding area under simple curves, area of the region bounded by a curve and a line, and area between two curves are the important topics covered in this chapter. practice class 12 maths chapter 8 ncert solutions to score well in the exam.

6. Which is the official website of NCERT ?

NCERT official is the official website of the "https://ncert.nic.in" where you can get NCERT textbooks and syllabus from class 1 to 12 that can be downloaded and studied offline. Careers360 created class 12 application of integrals ncert solutions. practice them to command the concepts.

7. What are the benefits of practicing class 12 application of integrals ncert solutions?

The class 12 application of integrals ncert solutions can be challenging as it incorporates numerous formulas and intricate concepts. To gain a solid understanding of each topic, students must regularly test their mathematical skills by practicing the questions provided. With consistent revision and diligent effort, students can confidently ace any exam, be it for their board exams or in a competitive setting.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:04 May,2024 - 04 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 29 January,2024
i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer
Upasana Barman 24 August,2022
i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.


As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.


Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.


Believe in Yourself! You can make anything happen


All the very best.

Read Complete Answer
Mayankjha.student2007 23 August,2022
if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects  and  we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer
Nuthalapati Vyshnavi 21 August,2022
I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer
Muskan Dhalwal 17 August,2022
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
March 22, 2024 - 08:10 PM IST :
February 02, 2024 - 03:48 PM IST :
January 04, 2024 - 06:06 PM IST :
CBSE Results 2024: Last 9 years’ CBSE Class 10, 12 result date and time; links to check score
May 01, 2024 - 03:34 PM IST
CBSE Board exams twice a year from 2025, no plan for semesters: MoE
April 26, 2024 - 07:45 PM IST
CBSE Class 12 board exams 2025 to have 50% competency-based questions; no change in 10th
April 04, 2024 - 03:43 PM IST
CBSE Class 12 board exams 2024 over; expected result date, trends of last 10 years
April 02, 2024 - 04:40 PM IST
CBSE Class 12 accountancy board exam analysis 2024 out; paper rated easy, balanced
March 23, 2024 - 05:04 PM IST
CBSE Class 12 biology paper 2024 today; know marking scheme, important topics
March 19, 2024 - 07:54 AM IST
CBSE Class 12 Exam 2024 Live: CBSE 12th Biology paper analysis, answer key, passing marks, result updates
March 18, 2024 - 05:29 PM IST

Stay up-to date with CBSE Class 12th News

Back to top