Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
Filter By
Clear Filter

All Questions

Write ‘True’ or ‘False’ and justify your answer in each of the following: AB is the diameter of a circle and AC is its chord such that \angleBAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.

First of all, we solve the question according to the given conditions. If we are able to prove it then it will be true otherwise it will be false.
Given:\angleBAC = 30^{\circ}
Diagram: Construct the figure according to the given conditions then join BC and OC.

To Prove: BC = BD
Proof :\angleBAC = 30^{\circ}    (Given)
\Rightarrow \, \angle BCD= 30^{\circ}
[\because angle between chord and tangent is equal to the angle made by chord in alternate segment]
\angle OCD= 90^{\circ} 
[\because Radius and tangent’s angle is always 90^{\circ}]
In \bigtriangleupOAC                    
OA = OC     (both are the radius of the circle)
\angle OCA= 30^{\circ}
\Rightarrow \angle OCA= 30^{\circ}  [opposite angles of an isosceles triangle are equal]
\therefore \; \; \angle ACD= \angle ACO+\angle OCD
= 30+90= 120^{\circ}
In \bigtriangleup ACD
\angle CAD+\angle ADC+\angle DCA= 180^{\circ}
[\because sum of an interior angle of a triangle 180^{\circ}]
30^{\circ}+\angle ADC+120^{\circ}= 180^{\circ}
\angle ADC= 180^{\circ}-120^{\circ}-30^{\circ}
< ADC=30^{\circ}
In \bigtriangleupBCD we conclude that
\angle BCD= 30^{\circ} and\angle ADC=30^{\circ} 
\Rightarrow BC= BD[\becausesides which are opposite to equal angles are always equal]
Hence Proved.
Hence the given statement is true.

View Full Answer(1)
Posted by

infoexpert27

Write ‘True’ or ‘False’ and justify your answer in each of the following: If several circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.

According to the question.

Here C1 and C2 circles pass through the points P and Q.
We know that the perpendicular bisector of the chord of a circle always passes through the centre of the circle. Hence the perpendicular bisector of line PQ passes through the centre of circles of C1, and C2.
Hence the given statement is True.

View Full Answer(1)
Posted by

infoexpert27

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

Write ‘True’ or ‘False’ and justify your answer in each of the following: If several circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.

 According to the question.

Here C1, C2, C3 are the circle with center O1, O2, O3 respectively.
C1, C2, C3 touches line PQ at point A. Here PQ is the tangent at each circle.
If we join O1, O2, and O3 to point A then the line is perpendicular to line PQ because if we draw a line from the centre of the circle at any point then the tangent at that point is perpendicular to the radius.
But here line joining the centres is not bisecting the line PQ because it depends on the length of PQ.
Hence the given statement is False.

View Full Answer(1)
Posted by

infoexpert27

Write ‘True’ or ‘False’ and justify your answer in each of the following: The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC


Given ABC is an isosceles triangle and AB = AC.

To Prove : XY\parallel BC
Proof: AB = AC     (Given)
\angle ABC= \angle ACB
[  The angle between the chord of a circle and tangent is equal to the angle made by the chord in an alternate segment]
Also \angle XAB= \angle ABC
\Rightarrow \angle XAB= \angle BCA
\Rightarrow XAY\parallel BC
i.e, \Rightarrow XY\parallel BC
Hence true                    

View Full Answer(1)
Posted by

infoexpert27

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Write ‘True’ or ‘False’ and justify your answer in each of the following: If the angle between two tangents drawn from a point P to a circle of radius a and centre O is 60^{\circ}, then. OP= a\sqrt{3}

Given \angle APB= 60^{\circ} 
Draw line OP from point O to P which bisects P. Which bisect \angle P
i.e, \angle APO= 30^{\circ}
In \bigtriangleup OAP
\sin 30^{\circ}= \frac{OA}{OP}
\therefore \sin \theta = \frac{perpendicular}{hypotenuse}
 
\frac{1}{2}= \frac{a}{OP}
OP = 2a

Hence the value of OP = 2a
Hence the given statement is False.

View Full Answer(1)
Posted by

infoexpert27

Write ‘True’ or ‘False’ and justify your answer in each of the following:If the angle between two tangents drawn from a point P to a circle of radius a and center O is 90^{\circ}, then OP= a\sqrt{2}

Answer True
Solution
            
Given  \angle APB= 90^{\circ}
Draw line OP from point O to P which bisects \angle P .
i.e, \angle OPB= 45^{\circ}
In \bigtriangleup OBP
\sin 45= \frac{OB}{OP}
\therefore \sin \theta = \frac{perpendicular}{hypotenuse}

\frac{1}{\sqrt{2}}= \frac{a}{OP}
OP= a\sqrt{2}
Hence the given statement is True.



 

View Full Answer(1)
Posted by

infoexpert27

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

Write ‘True’ or ‘False’ and justify your answer in each of the following :The angle between two tangents to a circle may be 0^{\circ}.

Answer True
Solution
It is possible that the angles of two line may be 0^{\circ} in only two conditions.
1. When lines are parallel
2.When both the lines are coincide.
Hence the given statement is True
This may be possible only when tangents are parallel or when both the tangents are coincide.

View Full Answer(1)
Posted by

infoexpert27

Write ‘True’ or ‘False’ and justify your answer in each of the following: The length of the tangent from an external point P on a circle with center O is always less than OP.

Answer True
Solution
             
 

Here O is the center of the given circle and PA is the tangent which is drawn from an external point P. OA is the radius of the circle. We know that tangent and radius are always perpendicular to each other.
\therefore \, \angle A= 90^{\circ}
 \therefore \bigtriangleup PAO is a right-angle triangle Use Pythagoras's theorem in \bigtriangleup PAO
       \left ( PO \right )^{2}= \left ( OA \right )^{2}+\left ( PA \right )^{2} …..(i)
From equation (i) we can say that PA is always less than PO.
In other words, we can say that the length of the hypotenuse is always greater than the length of the perpendicular in a right-angle triangle.
i.e.,      OP > PA
Hence the given statement is True.


   

View Full Answer(1)
Posted by

infoexpert27

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

Write ‘True’ or ‘False’ and justify your answer in each of the following: The length of the tangent from an external point on a circle is always greater than the radius of the circle.

Answer False
Solution
Case-I – When external point P is very close to the circle
      
Here C is the center of the circle. Let this radius be 5 and the distance of Px and Py is 3. Or we can say that Case I contradicts the given statement.
Case II – When external point P is far from the circle.
 
Here radius of the given circle is 5 cm and the length of Px and Py is 10 cm.
Hence according to Case II and given statement is True.
Hence from the above two cases, we conclude that the tangent’s length is dependent on the distance of an external point from the circle.
Therefore given statement is False because the length of the tangent from an external point of a circle may or may not be greater than the radius of the circle.
Therefore the given statement is False.

 

 

View Full Answer(1)
Posted by

infoexpert27

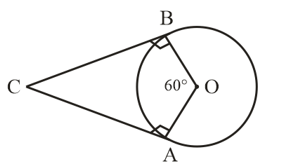
Write ‘True’ or ‘False’ and justify your answer in each of the following :
If a chord AB subtends an angle  60^{\circ} at the center of a circle, then the angle between the tangents at A and B is also 60^{\circ}.

Answer False
Solution
              
Here CA and CB are the two tangents which is drawn on chord AB and also we know that tangent and radius are perpendicular to each other.
i.e., \angle CBO=\angle CAO= 90^{\circ}
In quadrilateral, ABCD
\angle A+\angle B+\angle C+\angle O= 360^{\circ}
[\mathbb{Q}  Sum of interior angles of a quadrilateral is 360^{\circ}]
90^{\circ}+90^{\circ}+\angle C+60^{\circ}= 360^{\circ}
\angle C= 360^{\circ}-60^{\circ}-90^{\circ}-90^{\circ}
\angle C= 120^{\circ}
Here we conclude that the angle between the tangents at A and B is 120^{\circ}.

Therefore the given statement is False.


       

View Full Answer(1)
Posted by

infoexpert27

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE
filter_img