Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


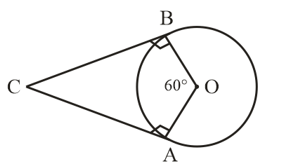
Write ‘True’ or ‘False’ and justify your answer in each of the following :
If a chord AB subtends an angle at the center of a circle, then the angle between the tangents at A and B is also
.
Answers (1)

Answer False
Solution
Here CA and CB are the two tangents which is drawn on chord AB and also we know that tangent and radius are perpendicular to each other.
i.e.,
In quadrilateral, ABCD
[ Sum of interior angles of a quadrilateral is
]
Here we conclude that the angle between the tangents at A and B is .
Therefore the given statement is False.
View full answer
Similar Questions
- Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up
- Use Euclid' s division algorithm to find the HCF of : 135 and 225
- Use Euclid' s division algorithm to find the HCF of :196 and 38220