-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
The equilibrium constant at 298 K for a reaction A+BC+D is 100. If the initial concentration of all the four species were 1 M each, then equilibrium concentration of D (in mol L−1) will be :
Option: 1 0.182
Option: 2 0.818
Option: 3 0.818
Option: 4 1.182
As we dicussed in the concept
Law of Chemical equilibrium -
At a given temperature, the product of concentration of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentration of the reactants raised to their individual stoichiometric coefficients has a constant value.
- wherein
are equilibrium concentration
For reaction
Initial concentration IM IM IM IM
At equilibarium if degree of dissociation is then
1- 1-
H
1+
9=
Concentration of D is 1+=I+
=1.818
View Full Answer(1) 50 mL of 0.2 M ammonia solution is treated with 25 mL of 0.2 M HCl. If pKb of ammonia solution is 4.75, the pH of the mixture will be :
Option: 1 3.75
Option: 2 4.75
Option: 3 8.25
Option: 4 9.25
Initially, before reaction
mmol of = 10
mmol of = 5
Therefore, after reaction,
mmol of = 5
mmol of = 5
Now, putting the values of concentrations in the equation
Thus, we have
Hence, the correct answer is Option (4)
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

Addition of sodium hydroxide solution to a weak acid (HA) results in a buffer of pH 6. If ionisation constant of HA is 10−5, the ratio of salt to acid concentration in the buffer solution will be :
Option: 1 4 : 5
Option: 2 1 : 10
Option: 3 10 : 1
Option: 4 5 : 4
As we learnt,
Hence, the correct answer is Option (3)
View Full Answer(1)Consider the following statements: (a) The pH of a mixture containing 400mL of 0.1 M H2SO4 and 400ml of 0.1M NaOH will be approximately 1.3. (b) Ionic product of water is temperature dependent. (c) A monobasic acid with has a pH=5. The degree of dissociation of this acid is 50%. (d) The Le Chatelier's principle is not applicable to common-ion effect. The correct statements are :
Option: 1 (a), (b) and (d)
Option: 2 (a), (b) and (c)
Option: 3 (b) and (c)
Option: 4 (a) and (b)
(a)
Mole of H2SO4 = 400 x 0.1 = 40
Mole of NaOH = 400 x 0.1 = 40
for 40 mol of H2SO4 , Need 80 mol of NaOH. But NaOH is 40 mol only.
So, NaOH is a limiting reagent.
Hence, 40 moles of NaOH will react with only 20 moles of H2SO4.
(b)
Thus, the ionic product of water is temperature-dependent.
(c)
Now,
(d) Le-chatelier's principle is applicable to the common ion effect.
So, statement (d) is wrong.
Therefore, option(2) is correct.
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Two solutions A and B each of 100L was made by dissolving 4g of NaOH and 9.8g of H2SO4 in water, respectively. The pH of the resultant solution obtained from mixing 40L of solution A and 10L of solution B is_________:
Option: 1 pH = 10.6
Option: 2 pH = 12.7
Option: 3 pH = 9.8
Option: 4 pH = 11
For given solutions, we have:
Moles of NaOH 4/40 = 0.1 moles
Moles of H2SO4 = 9.8/98 = 0.1 moles
Molarity of NaOH = 0.1/100L
And molarity of H2SO4 = 0.1/100
Now, 40L of NaOH solution and 10L of H2SO4 solution are added, thus we get:
Total volume = 50L
Milliequivalents of NaOH = 40x(0.1/100)x1 = 0.04
Milliequivalents of H2SO4 = 10x(0.2/100)x2 = 0.02
Thus, Meq of NaOH left = 0.04 - 0.02 = 0.02
[OH-] = 4x10-4
pOH = -log[4x10-4]
pOH = -log4 - log10-4
pOH = -0.60 + 4 = 3.4
Further, we know:
pH = 14 - 3.4
pH = 10.6
Hence, the option number (1) is correct.
View Full Answer(1)For the following Assertion and Reason, the correct option is : Assertion : The pH of water increases with increase in temperature. Reason : The dissociation of water into and
is an exothermic reaction.
Option: 1 Assertion is not true, but reason is true.
Option: 2 Both assertion and reason are true, and the reason is the correct explanation for the assertion.
Option: 3 Both assertion and reason are false.
Option: 4 Both assertion and reason are true, but the reason is not the correct explanation for the assertion.
The pH of water does not increase with the increase in temperature.
The dissociation of water molecules into ions is bond breaking and is, therefore, an endothermic process.
Therefore, Option(3) is correct.
View Full Answer(1)NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
3g of acetic acid is added to 250 mL of 0.1M HCl and the solution made up to 500 mL. To 20 mL of this solution mL. of 5 M NaOH is added. The pH of the solution is_______. [ Given: pKa of acetic acid = 4.75, molar mass of acertic acid = 60 g/mol, log3 = 0.4771] Neglect any chnages in volume.
Given,
m mole of acetic acid in 20 mL = 2
m mole of HCl in 20 mL = 1
m mole of NaOH = 2.5
2 3/2 0 0
0.5 0 3/2
pH = 4.74 + log 3
pH = 4.74 + 0.48 = 5.22
Thus, the correct answer is 5.22
Hence, the option number (1) is correct.
View Full Answer(1)Arrange the following solution in the decreasing order of 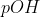 A)
A) 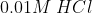 B)
B) 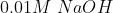 C)
C) 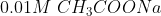 D)
D) 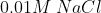
Option: 1 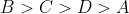
Option: 2 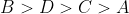
Option: 3 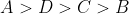
Option: 4 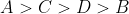
If is low(means more acidic) then
is high.
Thus, acidic order:
Then the order of will be:
Therefore, Option(3) is correct.
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

For the reaction:

Option: 1 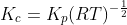
Option: 2 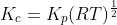
Option: 3 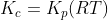
Option: 4 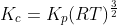
The reaction occurs as follows:
We know that:
Therefore, Option(2) is correct.
View Full Answer(1)If the solubility product of is
then the solubility of
in pure water is ________
[Assuming that neither kind of ion reacts with water]
If Solubility is s then

Ans = 2
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE


