Get Answers to all your Questions

Filter By

Clear Filter

All Questions

If the screw on the screw-gauge is given six rotations, it moves by 3 mm on the main scale. If there are 50 divisions on the circular scale the least count of the screw gauge is: (in cm)
Option: 1 0.001
Option: 2 0.01
Option: 3 0.02
Option: 4 0.001

Pitch $=\frac{3}{6} = 0.5mm$

L.C $= \frac{0.5mm}{50} = \frac{1}{100}mm = 0.01mm = 0.001cm$

Hence the option correct option is (1).

View Full Answer(1)

Posted by

avinash.dongre

In a Screw Gauge, fifth division of the circular scale coincides with the reference line when the ratchet is closed.There are 50 divisions on the circular scale,and the main scale moves by 0.5 mm on a complete rotation. For a particular observation the reading on the main scale is 5 mm and the 20^thdivision of the circular scale coincides with reference line. Calculate the true reading.
Option: 1 $5\cdot 20\, mm$
Option: 2 $5\cdot 00\, mm$
Option: 3 $5\cdot 15\, mm$
Option: 4 $5\cdot 25\, mm$

$\text{No of CSD} = 50$
$pitch= 0\cdot 5\, mm$
$MSR= 5\, mm$
$CSD= 20\, division$
$CSR= LC\times CSD$
            $= \left ( \frac{pitch}{\text{No of CSD}} \right )\times CSD$
           $= \frac{0\cdot 5\times 10^{-3}}{50}\times\, 20$
            $= 2\times 10^{-4}\, m$
$CSR=0\cdot 2\, mm$
$Zero\,\: error= \left ( LC \right )\times 5$
                         $= 10^{-5}\times5= 0\cdot 05\, mm$
$True\, reading= MSR+CSR+\left ( Zero\: conection \right )$
                             $= 5+0\cdot 2+\left ( -0\cdot 05 \right )$
$\rightarrow True\: reading= 5\cdot 15\, mm$
The correct option is (3)

View Full Answer(1)

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

For full scale deflection of total 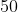$50$ divisions, 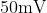$50 \mathrm{mV}$ voltage is required in galvanometer. The resistance of galvanometer if its current sensitivity is 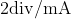$2 \mathrm{div} / \mathrm{mA}$ will be :

Option: 1 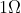$1\Omega$
Option: 2 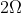$2 \Omega$
Option: 3 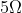$5 \Omega$
Option: 4 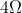$4 \Omega$

$\frac{d\theta}{di}= \frac{2div}{mA}\\$

For $50$ divisions,the corresponding current will be

$i_{g}= 25mA\\$

$V= 50mV= i_{g}\times R\\$

$R= 2\Omega$

View Full Answer(1)

Posted by

vishal kumar

The diameter of a spherical bob is measured using a vernier callipers. 9 divisions of the main scale, in the vernier callipers, are equal to 10 divisions of vernier scale. One main scale division is $1 \mathrm{~mm}.$ The main scale reading is $10 \mathrm{~mm}$ and $8^{\text {th }}$ division of vernier scale was found to coincide exactly with one of the main scale division. If the given vemier callipers has positive zero error of $0.04 \mathrm{~cm},$ then the radius of the bob is _________ $\times 10^{-2} \mathrm{~cm}$ .

$9MSD=10VSD\\$

$1MSD=1mm\\$

$LC=1MSD-1VSD=0.1MSD\\$

$MSR=10mm\\$

$VCD\: or\: VSD=8\\$

$Zero \ \ error=+0.04cm\\$

$Reading(Diameter)=MSR+VSR+Zero \ \ correction\\$

$=10mm+LC\times VCD+\left ( -Zero\: error \right )\\$

$=10mm+\left ( 0.1 \right )\times8+\left ( -0.4mm \right )\\$

$Diameter=10.4mm$

$Radius=5.2mm=52\times10^{-2}cm$

View Full Answer(1)

Posted by

Ritika Jonwal

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Assertion A : If in five complete rotations of the circular scale, the distance travelled on main scale of the screw gauge is 5 mm and there are 50 total divisions on circular scale, then least count is 0.001 cm. Reason R : $Least Count = \frac{Pitch }{Total\: \: divisions\: \: on\: \: circular\: \: scale}$ In the light of the above statements, choose the most appropriate answer from the options given below :
Option: 1 A is not correct but R is correct.
Option: 2 Both A and R are correct and R is the correct explanation of A.
Option: 3 A is correct but R is not correct.
Option: 4 Both A and R are correct and R is NOT the correct explanation of A.

Distance travelled on the main scale in one rotation is equal to pitch.

$$$ \begin{aligned} \therefore 5 \mathrm{~mm} &=5 \text { (pitch) } \\ \text { pitch } &=1 \mathrm{~mm} \rightarrow(1) \end{aligned}$

$\text{No. of CSD}=50\; \text{division}$

$\text{L.C}= \frac{\text{pitch}}{\text{No.of CSD}}$

$\begin{aligned} =\frac{1 \mathrm{~mm}}{50} &=0.02 \times 10^{-3} \mathrm{~m} \\ &=0.002 \mathrm{~cm} \end{aligned}$

The correct option is (1)

View Full Answer(1)

Posted by

vishal kumar

Student A and Student B used two screw gauges of equal pitch and 100 equal circular divisions to measure the radius of a given wire. The actual value of the radius of the wire is $0.322 \mathrm{~cm}$ . The absolute value of the difference between the final circular scale readings observed by the students $\mathrm{A}$ and $\mathrm{B}$ is__________.
[Figure shows position of reference $' O '$ when jaws of screw gauge are closed]
Given pitch $=0.1 \mathrm{~cm}.$

pitch= $0\cdot 1\, cm$
No.of circular divisions = 100
$Least\, count = \frac{pitch}{No.of \, circular \, division}$
                         $= 10^{-3}\, cm$
                         $= 0\cdot 001 cm$
Actual value of the radius of the wire $= 0\cdot 322 cm$
Let the main scale reading be X
$\left ( Reading \right )_{A}= MSR+CSR$
                         $= X+\left ( CSD \right )\times LC$
                        $= X+\left ( 5 \right )\times 0\cdot 001$
$R_{A}=X+0\cdot 005$
(i.e 5 divisions ahead of zero mark)
$\left ( Reading \right )_{B}= R_{B}= MSR+CSR$
                         $= \left ( X-1 \right )+\left ( CSD \right )\times \left ( LC \right )$
                         $= \left ( X-1 \right )+\left ( 92 \right )\times 0\cdot 001$
                          $=X-0\cdot 008$
(i.e 8 CSD behind zero mark )
$\Delta R= R_{A}-R_{B}= 0\cdot 013$
Reading corresponds to 13 circular scale division
The answer is 13

View Full Answer(1)

Posted by

vishal kumar

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

The varnier scale used for measurement has a positive zero error of 2.0 mm. If while taking a measurement it was noted that '0' on the vernier scale lies between 8.5 cm and 8.6 cm, vernier coincidence is 6, then the correct value of measurement is _______ cm. (least count = 0.01 cm)
Option: 1 8.56 cm

Option: 2 8.54 cm
Option: 3 8.58 cm
Option: 4 8.36 cm

Positive zero error =0.2 mm

Main scale reading =8.5 cm

Vernier scale reading = $6 \times 0.01=0.06 \mathrm{~cm}$

Final reading =8.5+0.06-0.02=8.54 cm

View Full Answer(1)

Posted by

avinash.dongre

Which of the following will NOT be observed when a multimeter (operating in resistance measuring mode ) probes connected across a component, are just reversed ?
Option: 1 Multimeter shows an equal deflection in both case i,e. before and after reversing the probes if the chosen component is resistor.
Option: 2 Multimeter shows NO deflection in both case i,e. before and after reversing the probes if the chosen component is capacitor.
Option: 3 Multimeter shows a deflection, accompanied by a splash of light out of connected component in one direction and NO deflection on reversing the probes if the chosen component is LED.
Option: 4 Multimeter shows NO deflection in both case i,e. before and after reversing the probes if the chosen component is metal wire.

1.No matter, how we connect the resistance across multimeter It shows the same deflection.

2.Multimeter shows deflection when it connects with a capacitor.

So option 2 is the answer.

3.If we assume that LED has negligible resistance then the multimeter shows no deflection for the forward bias but when it connects in the reverse direction, it break down occurs so splash of light out.

4.The resistance of the metal wire may be taken zero, so no deflection in the multimeter.

View Full Answer(1)

Posted by

avinash.dongre

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

Using a screw ganged pitch $0.1\; cm$ and 50 divisions of its circular scale, the thickness of an object is measured. It should correctly be recorded as :

Option: 1 2.124
Option: 2 2.21
Option: 3 2.125
Option: 4 2.127

Pitch of the circular scale $\mathrm{P}=0.1 \mathrm{cm}$

Number of divisions on a circular scale $N=50$

So least count of screw gauge $L C=\frac{P}{N}=\frac{0.1}{50} \mathrm{cm}=0.002 \mathrm{cm}$

So any measurement will be integral Multiple of LC
From the option, we can say that The answer will be 2.124 cm

View Full Answer(1)

Posted by

avinash.dongre

One main scale division of a vernier callipers is 'a' cm and n^th division of the vernier scale coincide with $(n-1)^{th}$ division of the main scale. The least count of the callipers in mm is :

Option: 1 $\frac{10 a}{n}$
Option: 2 $\left ( \frac{n-1}{10n} \right )a$
Option: 3 $\frac{10\; na}{(n-1)}$
Option: 4 $\frac{10 a}{(n-1)}$

As n^th division of the vernier scale coincide with $(n-1)^{th}$ division of the main scale

$\begin{array}{l} (\mathrm{n}-1) \mathrm{a}=\mathrm{n}\left(\mathrm{a}^{\prime}\right) \\ \\ \Rightarrow \mathrm{a}^{\prime}=\frac{(\mathrm{n}-1) \mathrm{a}}{\mathrm{n}} \end{array}$

Where $\mathrm{a}^{\prime}$ is the One main scale division of vernier calipers.

$\begin{aligned} \therefore \mathrm{L.C} &=1 \mathrm{MSD}-1 \mathrm{VSD} \\ &=\left(\mathrm{a}-\mathrm{a}^{\prime}\right) \mathrm{cm} \\ &=\mathrm{a}-\frac{(\mathrm{n}-1) \mathrm{a}}{\mathrm{n}} \\ &=\frac{\mathrm{na}-\mathrm{na}+\mathrm{a}}{\mathrm{n}}=\frac{\mathrm{a}}{\mathrm{n}} \mathrm{cm} \end{aligned}$

$LC=\frac{10a}{n}\ mm$

View Full Answer(1)

Posted by

avinash.dongre

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Top Schools

Products & Resources

NCERT Solutions

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

If the screw on the screw-gauge is given six rotations, it moves by 3 mm on the main scale. If there are 50 divisions on the circular scale the least count of the screw gauge is: (in cm) Option: 1 0.001 Option: 2 0.01 Option: 3 0.02 Option: 4 0.001

Posted by

avinash.dongre

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

For full scale deflection of total divisions, voltage is required in galvanometer. The resistance of galvanometer if its current sensitivity is will be : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

vishal kumar

Posted by

Ritika Jonwal

JEE Main high-scoring chapters and topics

Posted by

vishal kumar

Posted by

If the screw on the screw-gauge is given six rotations, it moves by 3 mm on the main scale. If there are 50 divisions on the circular scale the least count of the screw gauge is: (in cm)
Option: 1 0.001
Option: 2 0.01
Option: 3 0.02
Option: 4 0.001

For full scale deflection of total $50$ divisions, $50 \mathrm{mV}$ voltage is required in galvanometer. The resistance of galvanometer if its current sensitivity is $2 \mathrm{div} / \mathrm{mA}$ will be :

Option: 1 $1\Omega$
Option: 2 $2 \Omega$
Option: 3 $5 \Omega$
Option: 4 $4 \Omega$

Using a screw ganged pitch $0.1\; cm$ and 50 divisions of its circular scale, the thickness of an object is measured. It should correctly be recorded as :

Option: 1 2.124
Option: 2 2.21
Option: 3 2.125
Option: 4 2.127