Q&A - Ask Doubts and Get Answers

The value of $\cos ^{3}\left ( \frac{\pi }{8} \right )\cdot \cos \left ( \frac{3\pi }{8} \right )+\sin ^{3}\left ( \frac{\pi }{8} \right )\cdot \sin \left ( \frac{3\pi }{8} \right )$ is :
Option: 1 $\frac{1}{4}$

Option: 2 $\frac{1}{2\sqrt{2}}$

Option: 3 $\frac{1}{2}$

Option: 4 $\frac{1}{\sqrt{2}}$

Trigonometric Identities -

Trigonometric Identities-

These identities are the equations that hold true regardless of the angle being chosen.

$\\\mathrm{\sin^2\mathit{t}+\cos^2\mathit{t}=1}\\\mathrm{1+\tan^2\mathit{t}=\sec^2\mathit{t}}\\\mathrm1+{\cot^2\mathit{t}=\csc^2\mathit{t}}\\\mathrm{\tan \mathit{t}=\frac{\sin \mathit{t}}{\cos \mathit{t}},\;\;\cot \mathit{t}=\frac{\cos\mathit{t}}{\sin\mathit{t}}}$

-

Allied Angles (Part 1) -

Allied Angles (Part 1)

Two angles or numbers are called allied iff their sum or difference is a multiple of π/2

sin (90⁰ - θ) = cos (θ)
cos (90⁰ - θ) = sin (θ)
tan (90⁰ - θ) = cot (θ)
csc (90⁰ - θ) = sec (θ)
sec (90⁰ - θ) = csc (θ)
cot (90⁰ - θ) = tan (θ)

sin (90⁰ + θ) = cos (θ)
cos (90⁰ + θ) = - sin (θ)
tan (90⁰ + θ) = - cot (θ)
csc (90⁰ + θ) = sec (θ)
sec (90⁰ + θ) = - csc (θ)
cot (90⁰ + θ) = - tan (θ)

-

$\\\cos ^3\:\frac{\pi }{8}\cos \frac{3\:\pi }{8}+\sin ^3\frac{\pi }{8}\:\sin \frac{3\:\pi }{8}\\\sin\left ( \frac{\pi}{2}-\frac{3\pi}{8} \right )=\cos\left ( \frac{3\pi}{8} \right )=\sin\left ( \frac{\pi}{8} \right )\\\\\\\cos ^3\:\frac{\pi }{8}\sin \frac{\:\pi }{8}+\sin ^3\frac{\pi }{8}\:\cos \frac{\:\pi }{8}\\\sin\frac{\pi}{8}\cos\frac{\pi}{8}\left ( \cos ^2\:\frac{\pi }{8}+\sin ^2\:\frac{\pi }{8} \right )\\\frac{1}{2}\left ( 2\:\sin \frac{\pi }{8}\cos \:\frac{\pi \:}{8} \right )=\frac{1}{2}\:\sin \frac{2\pi }{8}=\frac{1}{2\sqrt2}$

View Full Answer(1)

Posted by

avinash.dongre

The strength of an aqueous NaOH solution is most accurately determined by titrating:
(Note: consider that an appropriate indicator is used)
Option: 1 Aq.NaOH in a pipette and aqueous oxalic acid in a burette
Option: 2 Aq.NaOH in a volumetric flask and concentrated $H_{2}SO_{4}$ in a conical flask
Option: 3 Aq.NaOH in a burette and concentrated $H_{2}SO_{4}$ in a conical flask
Option: 4 Aq.NaOH in a burette and aqueous oxalic acid in a conical flask

As we have learnt,

To calculate the strength of NaOH, it is titrated against oxalic acid. For this purpose, NaOH is kept in a burette and oxalic acid in a conical flask.

Therefore, Option(4) is correct.

View Full Answer(1)

Posted by

vishal kumar

If $\frac{\sqrt{2}\sin \alpha }{\sqrt{1+\cos 2\alpha }}=\frac{1}{7}$ and $\sqrt{\frac{1-\cos 2\beta }{2}}=\frac{1}{\sqrt{10}},$ $\alpha ,\beta\; \epsilon \left ( 0,\frac{\pi }{2} \right ),$ then $\tan \left ( \alpha +2\beta \right )$ is equal to ________.
Option: 1 $0$
Option: 2 $1$
Option: 3 $0.5$
Option: 4 $2$

Trigonometric Identities -

Trigonometric Identities-

These identities are the equations that hold true regardless of the angle being chosen.

$\\\mathrm{\sin^2\mathit{t}+\cos^2\mathit{t}=1}\\\mathrm{1+\tan^2\mathit{t}=\sec^2\mathit{t}}\\\mathrm1+{\cot^2\mathit{t}=\csc^2\mathit{t}}\\\mathrm{\tan \mathit{t}=\frac{\sin \mathit{t}}{\cos \mathit{t}},\;\;\cot \mathit{t}=\frac{\cos\mathit{t}}{\sin\mathit{t}}}$

-

Double Angle Formula and Reduction Formula -

Double Angle Formula and Reduction Formula

$\begin{aligned} \sin (2 \theta) &=2 \sin \theta \cos \theta \\&=\frac{2\tan\theta}{1+\tan^2\theta} \\\cos (2 \theta) &=\cos ^{2} \theta-\sin ^{2} \theta \\ &=1-2 \sin ^{2} \theta \\ &=2 \cos ^{2} \theta-1\\&=\frac{1-\tan^2\theta}{1+\tan^2\theta} \\ \tan (2 \theta) &=\frac{2 \tan \theta}{1-\tan ^{2} \theta} \end{aligned}$

$\begin{aligned} \tan (\alpha+\beta) &=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\ \tan (\theta+\theta) &=\frac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta} \\ \tan (2 \theta) &=\frac{2 \tan \theta}{1-\tan ^{2} \theta} \end{aligned}$

-

$\\\frac{\sqrt{2} \sin \alpha}{\sqrt{2} \cos \alpha}=\frac{1}{7}\\\tan\alpha=\frac{1}{7}\\\sin\beta=\frac{1}{\sqrt{10}}\\\tan\beta=\frac{1}{\sqrt{3}}\\\tan 2 \beta=\frac{2 \cdot \frac{1}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4}\\\tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta}=1$

Correct Option (2)

View Full Answer(1)

Posted by

vishal kumar

Reaction of an inorganic sulphite X with dilute 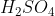$H_{2}SO_{4}$ generates compound Y.Reaction of Y with 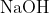$\mathrm{NaOH}$ gives X. Further, the reaction of X with Y and water affords compound Z. Y and Z, respectively, are :
Option: 1 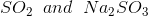$SO_{2}\; \; and \; \; Na_{2}SO_{3}$
Option: 2 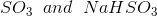$SO_{3}\; \; and \; \; NaHSO_{3}$
Option: 3 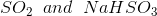$SO_{2}\; \; and \; \; NaHSO_{3}$
Option: 4 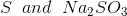$S\; \; and \; \; Na_{2}SO_{3}$

The reaction will be-

So, Y and Z, respectively, are $SO_{2}\; \; and \; \; NaHSO_{3}$

Therefore, the correct option is (3).

View Full Answer(1)

Posted by

Kuldeep Maurya

If you spill a chemical toilet cleaning liquid on your hand, your first aid would be:
Option: 1 aqueous NH₃
Option: 2 gaseous NaHCO₃
Option: 3 aqueous NaOH
Option: 4 Vinegar

Chemical toilet cleaning liquid contains acid and hence the first aid would be a weak base like NaHCO₃.

Therefore, Option(2) is correct.

View Full Answer(1)

Posted by

Kuldeep Maurya

Two poles, $A B$ of length a metres and $C D$ of length $a+b(b \neq a)$ metres are erected at the same horizontal level with bases at $\mathrm{B}$ and $\mathrm{D}$ . If $\mathrm{BD}=x$ and $\tan \angle \mathrm{ACB}=\frac{1}{2}$ , then :
Option: 1 $x^{2}-2 \mathrm{a} x+\mathrm{a}(\mathrm{a}+\mathrm{b})=0$
Option: 2 $x^{2}+2(\mathrm{a}+2 \mathrm{~b}) x-\mathrm{b}(\mathrm{a}+\mathrm{b})=0$
Option: 3 $x^{2}+2(\mathrm{a}+2 \mathrm{~b}) x+\mathrm{a}(\mathrm{a}+\mathrm{b})=0$
Option: 4 $x^{2}-2 \mathrm{a} x+\mathrm{b}(\mathrm{a}+\mathrm{b})=0$

$\angle ACB= \angle ACD-\angle BCD\\$

$\Rightarrow \tan\angle ACB=\tan\left ( \angle ACD-\angle BCD \right )\\$

$\tan\angle ACD= \frac{x}{b}, \tan\angle BCD= \frac{x}{a+b}\\$

$\Rightarrow \frac{1}{2}= \frac{\frac{x}{b}-\frac{x}{a+b}}{1+\frac{x}{b}\cdot \frac{x}{a+b}}\\$

$\Rightarrow \frac{1}{2}= \frac{\left ( a+b \right )x-bx}{b\left ( a+b \right )+x^{2}}\\$

$\Rightarrow x^{2}-2ax+b\left ( a+b \right )= 0$

View Full Answer(1)

Posted by

Kuldeep Maurya

The addition of dilute $\mathrm{NaOH}$ to $\mathrm{Cr}^{3+}$ salt solution will give :
Option: 1 Precipitate of 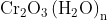$\mathrm{Cr}_{2} \mathrm{O}_{3} \left(\mathrm{H}_{2} \mathrm{O}\right)_{\mathrm{n}}$
Option: 2 Precipitate of 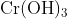$\mathrm{Cr}(\mathrm{OH})_{3}$
Option: 3 Precipitate of $\left[\mathrm{Cr}(\mathrm{OH})_{6}\right]^{3-}$
Option: 4 A solution of $\left[\mathrm{Cr}(\mathrm{OH})_{4}\right]^{-}$

Addition of dilute $\mathrm{NaOH}$ to a salt solution of $\mathrm{Cr^{3+}}$ will lead to the formation of a precipitate of hydrated chromium (III) oxide.

$\mathrm{Cr}^{3+}+\underset{\mathrm{dil}}{\mathrm{NaOH}} \longrightarrow \mathrm{Cr}_{2} \mathrm{O}_{3} \cdot \mathrm{nH}_{2} \mathrm{O}$

Hence, the correct answer is option (1)

View Full Answer(1)

Posted by

sudhir.kumar

Acidic ferric chloride solution on treatment with excess of potassium ferrocyanide gives a Prussian blue coloured colloidal species. It is :
Option: 1 $\mathrm{HFe}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]$
Option: 2 $\mathrm{K}_{5} \mathrm{Fe}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]_{2}$
Option: 3 $\mathrm{Fe}_{4}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]_{3}$
Option: 4 $\mathrm{KFe}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]$

$\mathrm{Fe^{3+}}$ ions react with excess of potassium ferrocyanide to form $\mathrm{KFe\left [ Fe\left ( CN \right )_{6} \right ]}$ .

The reaction is given below:

$\mathrm{\underset{excess}{K_{4}\left [ Fe\left ( CN \right ) _{6}\right ]}+Fe^{3+}\rightarrow KFe\left [ Fe\left ( CN \right )_{6} \right ]}$

Hence,the correct answer is Option (4)

View Full Answer(1)

Posted by

sudhir.kumar

Match List - I with List - II :

List-I (Metal Ion) List-II (Group in Qualitative analysis)

$(a) \mathrm{Mn}^{2+}$ (i) Group - III

$(b) \mathrm{As}^{3+}$ (ii) Group - IIA

$(c) \mathrm{Cu}^{2+}$ (iii) Group - IV

$(d) \mathrm{Al}^{3+}$ (iv) Group - IIB

Choose the most appropriate answer from the options given below :
Option: 1 $(a)-(iii), (b)-(iv), (c)-(ii), (d)-(i)$
Option: 2 $(a)-(iv), (b)-(ii), (c)-(iii), (d)-(i)$
Option: 3 $(a)-(i), (b)-(iv), (c)-(ii), (d)-(iii)$
Option: 4 $(a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)$

The correct match of basic radicalsand their groups in Qualitative analysis is given below

$\mathrm{(a)Mn^{2+}:Group\; I V (iii)}$

$\mathrm{(b)As^{3+}:Group\; IIB(iv)}$

$\mathrm{(c)Cu^{2+}:Group\; II A(ii)}$

$\mathrm{(d)Al^{3+}: Group (III)(i )}$

Hence the correct answer is option (1)

View Full Answer(1)

Posted by

sudhir.kumar

Consider the sulphides $\mathrm{HgS}$, $\mathrm{PbS}$, $\mathrm{CuS}_{}, \mathrm{Sb}_{2} \mathrm{~S}_{3},\mathrm{As}_{2} \mathrm{~S}_{3}$ and $\mathrm{CdS}$ . Number of these sulphides soluble in $50 \% \mathrm{HNO}_{3}$ is_________.

The sulphide which are soluble in $\mathrm{50% \ HNO_{3}}$ are $\mathrm{PbS,\ CuS,\ As_{2}S_{3},\ CdS}$

Sulphides insoluble in $\mathrm{50%\ HNO_{3}}$ are $\mathrm{HgS}$ and $\mathrm{Sb_{2}S_{3}}$

Hence, the correct answer is 4

View Full Answer(1)

List-I (Metal Ion)	List-II (Group in Qualitative analysis)
$(a) \mathrm{Mn}^{2+}$	(i) Group - III
$(b) \mathrm{As}^{3+}$	(ii) Group - IIA
$(c) \mathrm{Cu}^{2+}$	(iii) Group - IV
$(d) \mathrm{Al}^{3+}$	(iv) Group - IIB

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Top Schools

Products & Resources

NCERT Study Material

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

The value of is : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

avinash.dongre

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

If and then is equal to ________. Option: 1 Option: 2 Option: 3 Option: 4

Posted by

vishal kumar

Reaction of an inorganic sulphite X with dilute generates compound Y.Reaction of Y with gives X. Further, the reaction of X with Y and water affords compound Z. Y and Z, respectively, are :Option: 1 Option: 2 Option: 3 Option: 4

Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

If you spill a chemical toilet cleaning liquid on your hand, your first aid would be:Option: 1 aqueous NH3 Option: 2 gaseous NaHCO3Option: 3 aqueous NaOHOption: 4 Vinegar

Posted by

If you spill a chemical toilet cleaning liquid on your hand, your first aid would be:
Option: 1 aqueous NH₃
Option: 2 gaseous NaHCO₃
Option: 3 aqueous NaOH
Option: 4 Vinegar

Consider the sulphides $\mathrm{HgS}$, $\mathrm{PbS}$, $\mathrm{CuS}_{}, \mathrm{Sb}_{2} \mathrm{~S}_{3},\mathrm{As}_{2} \mathrm{~S}_{3}$ and $\mathrm{CdS}$ . Number of these sulphides soluble in $50 \% \mathrm{HNO}_{3}$ is_________.