Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • A point source of light is placed at the centre of curvature of a hemispherical surface. The radius of curvature is  <img alt="r" src="https://entrancecorner.oncodecogs.com/gif.latex?r" /

A point source of light is placed at the centre of curvature of a hemispherical surface. The radius of curvature is  r and the inner surface is completely refleciting. Find the force on the hemisphere due to the light falling on it if the source emits a power W.

Option: 1

\frac{ \mathrm{~W}}{\mathrm2{c}}


Option: 2

\frac{W}{c}


Option: 3

\frac{2 \mathrm{~W}}{\mathrm{c}}


Option: 4

\frac{4 \mathrm{~W}}{\mathrm{c}}


Answers (1)

best_answer

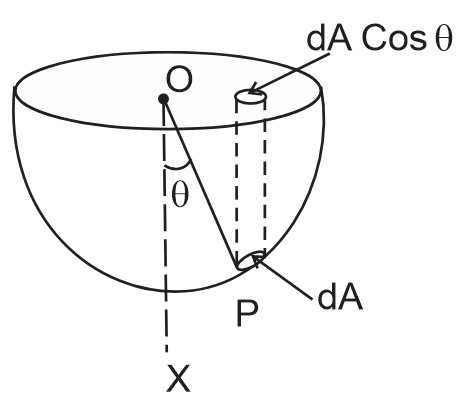
the energy emitted by the source per unit time i.e. W

fall on a area 4 \pi r^2  at a distance r. per unit time is \frac{W}{4 \pi r^2}

consider a small   area d A at the point P of the hemisphere

\Rightarrow energy facing per unit time on it is.
P=\frac{\operatorname{W} d A}{4 \pi r^2}

The corresponding momentum incident on this area per unit time is \frac{\operatorname{W d} A}{4 \pi r^2 c}.
suppose the radius OP through the area dA makes an angle \theta with the symmetry axis OX.

The forces on dA is along this radius d f=\frac{\2W d A}{4 \pi r^2 c}.


By symmetry the resultant force on the hemisphere is along OX,

the component of dF along OX is
d F \cos \theta=\frac{2 W d A}{4 \pi r^2 c} \cos \theta=\frac{2 W}{4 \pi r^2 c} ( projection of d A on the plane containing the rim)
\Rightarrow Net force along OX is
F=\frac{2 \mathrm{~W}}{4 \pi r^2 c} \sum (Projection of the area dA on plane containing rim)


=\frac{2 W}{4 \pi r^2 c} \cdot \pi r^2=\frac{W}{2 c}.

Posted by

Ritika Harsh

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2026 application correction begins on jeemain.nta.nic.in; edit details by December 2
anam-khan

JEE Mains 2026 LIVE: NTA to conduct session 1 from January 21 to 30; exam pattern, syllabus
anam-khan

JEE Main 2026 correction window opens tomorrow; NTA allows exam city change

Latest Question