Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • A train has just completed a U-curve in a track which is a semicircle. The engine is at the forward end of the semi circular part of the track while the last carriage is

A train has just completed a U-curve in a track which is a semicircle. The engine is at the forward end of the semi circular part of the track while the last carriage is at the rear end of the semicircular track. The driver blows a whistle of frequency 150 Hz. Velocity of sound is 340 m/sec. Then the apparent frequency as observed by a passenger in the middle of a train when the speed of the train is 60 m/sec ?

Option: 1

150 \mathrm{~Hz}


Option: 2

200 \mathrm{~Hz}


Option: 3

250 \mathrm{~Hz}


Option: 4

300 \mathrm{~Hz}


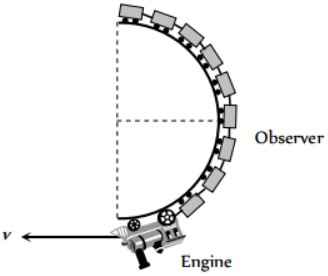
Answers (1)

best_answer

The Doppler formula holds for non-collinear motion if vs and v0 are taken to be the resolved component along the line of sight, In this case, we have:

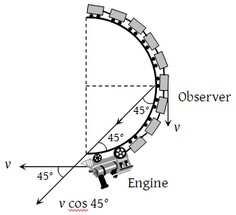
The component of velocity of source along the time joining the observer and source is:

\mathrm{V}_{\mathrm{s}}=-60 \cos 45^{\circ} \mathrm{m} / \mathrm{s}=\frac{-60}{\sqrt{2}} \mathrm{~m} / \mathrm{s}

The component of velocity of observer towards source is:

V_0=-60 \cos 45^{\circ} \mathrm{m} / \mathrm{s}=\frac{-60}{\sqrt{2}} \mathrm{~m} / \mathrm{s}

\mathrm{V}=340 \mathrm{~m} / \mathrm{s}

\mathrm{f}=150 \mathrm{~Hz}

By Doppler's effect formula, the apparent frequency f’ is given by:

\begin{aligned} f^{\prime} & =f\left(\frac{V-V_0}{V-V_s}\right) \\ f^{\prime} & =150\left(\frac{340-\left(\frac{-60}{\sqrt{2}}\right)}{340-\left(\frac{-60}{\sqrt{2}}\right)}\right) \end{aligned}

f^{\prime}=150 \mathrm{~Hz}

In this case, the apparent frequency observed by the passenger in the middle of the train is

150 \mathrm{~Hz}

Posted by

Devendra Khairwa

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2026: NTA directs non-Aadhaar applicants to submit photo verification certificate by January 7
anam-khan

Jharkhand CM inaugurates free coaching institute for tribal medical, engineering students
anam-khan

JEE Main 2026: IIT Roorkee’s ECE emerges as top choice after CSE; closing rank rises

Latest Question