Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • In the circuit shown in figure. is a variable <img alt="" src="https://cdn.entrance360.com/me

In the circuit shown in figure. (A), R_3 is a variable


resistance. As the value R_3 is changed, current  I  though the cell varies as shown. Obviously, the variation is asymptotic, i.e. I \rightarrow 6 \mathrm{~A} as R_3 \rightarrow \infty. Resistances R_1 and R_2 are, respectively -
 

Option: 1

4 \Omega, 2 \Omega


Option: 2

2 \Omega, 4 \Omega


Option: 3

2 \Omega, 2 \Omega


Option: 4

1 \Omega, 4 \Omega


Answers (1)

best_answer

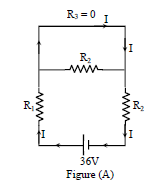
For R_3=0, I=9 A (from the graph). In this situation, the circuit can be drawn as shown in figure (A).

Here I=\frac{36}{R_1+R_2}=9
or\mathrm{R}_1+\mathrm{R}_2=4 \quad \quad \quad \dots(1)

For \mathrm{R}_3 \rightarrow \infty, equivalent resistance of \mathrm{R}_2 \text{ and }\mathrm{R}_3 in parallel will be
\begin{aligned} \frac{1}{R_{e q}} & =\frac{1}{R_2}+\frac{1}{R_3 \rightarrow \infty} \\ & =\frac{1}{R_2} \end{aligned}
[Current through R_2 will be zero because we have a short circuit \left(R_3=0\right. ) across \mathrm{R}_2]

or \mathrm{R}_{\mathrm{eq}}=\mathrm{R}_2
In this situation, the circuit can be drawn as shown figure (B).


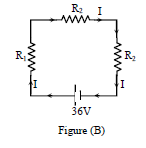
\begin{aligned} \text { Now } I & =\frac{36}{R_1+2 R_2} \\ & =6 \quad \quad (given) \\ \therefore R_1 & +2 R_2=6 \quad \quad \dots(2) \end{aligned}
from eqs. (1) and (2)
\mathrm{R}_1=2 \Omega, \mathrm{R}_2=2 \Omega

Posted by

seema garhwal

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2026 application correction begins on jeemain.nta.nic.in; edit details by December 2
anam-khan

JEE Mains 2026 LIVE: NTA to conduct session 1 from January 21 to 30; exam pattern, syllabus
anam-khan

JEE Main 2026 correction window opens tomorrow; NTA allows exam city change

Latest Question