Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
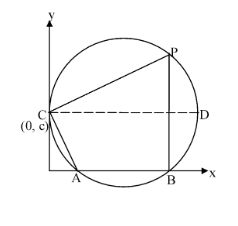
  • In the figure shown two points A(a,0) and B(b,0) are given on x −axis and a third point C(0,c) on y−axis. Find the locus of P such that the four A, B, P and C lie in a circle and h

In the figure shown two points A(a,0) and B(b,0) are given on x −axis and a third point C(0,c) on y−axis. Find the locus of P such that the four A, B, P and C lie in a circle and hence find the coordinates of point D on locus of P such that AB || CD.

Option: 1

(a+b, c)


Option: 2

(a-b, c)


Option: 3

(a b, c)


Option: 4

(a, c+b)


Answers (1)

best_answer

Clearly a circle can pass through the four vertices of quadrilateral ABPC if the four points A, B, P, C are vertices of a cyclic quadrilateral. Since one and only one circle can pass through three distinct and non-collinear points, therefore, the required locus will be the circle which passes through the given points A, B, C. Let the equation of the circle be given a

\mathrm{(x-\alpha)^2+(y-\beta)^2=r^2} ------------(1)

Since it passes through point A, B, C we have

\mathrm{\left.\begin{array}{l} r^2=(a-\alpha)^2+\beta^2 \\ r^2=(b-\alpha)^2+\beta^2 \\ r^2=\alpha^2+(c-\beta)^2 \end{array}\right]}-----------(2)

On solving equations (2) we find

\alpha=\frac{a+b}{2} \quad \beta=\frac{c^2+a b}{2 c} \text { and } \mathrm{r}=\frac{\sqrt{c^4+a^2 b^2+b^2 c^2+c^2 a^2}}{2 c}

Thus equation of the locus of P is

\mathrm{\left(x-\frac{a+b}{2}\right)^2+\left(y-\frac{c^2+a b}{2 c}\right)^2=\frac{c^4+a^2 b^2+b^2 c^2+c^2 a^2}{4 c^2}}-----(3)

The coordinates of point D satisfying the given condition AB|| CD can be obtained by substituting y = c in the equation of locus of P.

\mathrm{\left(x-\frac{a+b}{2}\right)^2+\left(c-\frac{c^2+a b}{2 c}\right)^2=\frac{c^4+a^2 b^2+b^2 c^2+c^2 a^2}{4 c^2}}on solving it we find

 x = a + b

Hence coordinates of D satisfying given condition are (a + b, c).

 

 

 

 

 

 

Posted by

himanshu.meshram

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2026 application correction begins on jeemain.nta.nic.in; edit details by December 2
anam-khan

JEE Mains 2026 LIVE: NTA to conduct session 1 from January 21 to 30; exam pattern, syllabus
anam-khan

JEE Main 2026 correction window opens tomorrow; NTA allows exam city change

Latest Question