NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.1

Q1 (i) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (i) The taxi fare after each km when the fare is $\small Rs\hspace{1mm}15$ for the first km and $\small Rs\hspace{1mm}8$ for each additional $\small km$ .

Answer:

It is given that
Fare for $1^{st} \ km$ = Rs. 15
And after that $\small Rs\hspace{1mm}8$ for each additional $\small km$
Now,
Fare for $2^{nd} \ km$ = Fare of first km + Additional fare for 1 km
= Rs. 15 + 8 = Rs 23

Fare for $3^{rd} \ km$ = Fare of first km + Fare of additional second km + Fare of additional third km
= Rs. 23 + 8= Rs 31

Fare of n km = $15 + 8 \times (n - 1)$
( We multiplied by n - 1 because the first km was fixed and for rest, we are adding additional fare.

In this, each subsequent term is obtained by adding a fixed number (8) to the previous term.)

Now, we can clearly see that this is an A.P. with the first term (a) = 15 and common difference (d) = 8

Q1 (ii) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (ii) The amount of air present in a cylinder when a vacuum pump removes $\small \frac{1}{4}$ of the air remaining in the cylinder at a time.

Answer:

It is given that
vacum pump removes $\small \frac{1}{4}$ of the air remaining in the cylinder at a time
Let us take initial quantity of air = 1

Now, the quantity of air removed in first step = 1/4

Remaining quantity after 1^st step

$= 1-\frac{1}{4}= \frac{3}{4}$

Similarly, Quantity removed after 2^nd step = Quantity removed in first step $\times$ Remaining quantity after 1^st step

$=\frac{3}{4}\times \frac{1}{4}= \frac{3}{16}$
Now,

Remaining quantity after 2^nd step would be = Remaining quantity after 1^st step - Quantity removed after 2^nd step

$=\frac{3}{4}- \frac{3}{16}= \frac{12-3}{16}= \frac{9}{16}$
Now, we can clearly see that

After the second step the difference between second and first and first and initial step is not the same, hence

the common difference (d) is not the same after every step

Therefore, it is not an AP

Q1 (iii) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (iii) The cost of digging a well after every meter of digging, when it costs $\small Rs\hspace{1mm}150$ for the first metre and rises by $\small Rs\hspace{1mm}50$ for each subsequent meter.

Answer:

It is given that
Cost of digging of 1st meter = Rs 150
and
rises by $\small Rs\hspace{1mm}50$ for each subsequent meter
Therefore,

Cost of digging of first 2 meters = cost of digging of first meter + cost of digging additional meter

Cost of digging of first 2 meters = 150 + 50

= Rs 200

Similarly,
Cost of digging of first 3 meters = cost of digging of first 2 meters + cost of digging of additional meter

Cost of digging of first 3 meters = 200 + 50

= Rs 250

We can clearly see that 150, 200,250, ... is in AP with each subsequent term is obtained by adding a fixed number (50) to the previous term.

Therefore, it is an AP with first term (a) = 150 and common difference (d) = 50

Q1 (iv) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (iv) The amount of money in the account every year, when $\small Rs\hspace{1mm}10000$ is deposited at compound interest at $\small 8\hspace{1mm}\%$ per annum.

Answer:

Amount in the beginning = Rs. 10000

Interest at the end of 1st year at the rate of $\small 8\hspace{1mm}\%$
is $\small 8\hspace{1mm}\%$ of 10000 = $\frac{8\times 10000}{100}= 800$

Therefore, amount at the end of 1st year will be

= 10000 + 800

= 10800

Now,

Interest at the end of 2nd year at rate of $\small 8\hspace{1mm}\%$
is $\small 8\hspace{1mm}\%$ of 10800 = $\frac{8\times 10800}{100}= 864$

Therefore,, amount at the end of 2^ndyear

= 10800 + 864 = 11664

Since each subsequent term is not obtained by adding a unique number to the previous term; hence, it is not an AP

Q2 (i) Write first four terms of the AP, when the first term a and the common difference d are given as follows $\small a=10,d=10$

Answer:

It is given that
$\small a=10,d=10$
Now,
$a_1= a =10$
$a_2= a_1 + d= 10 + 10 = 20$
$a_3= a_2 + d= 20 + 10 = 30$
$a_4= a_3 + d= 30 + 10 = 40$
Therefore, the first four terms of the given series are 10,20,30,40

Q2 (ii) Write first four terms of the AP when the first term a and the common difference d are given as follows: $\small a=-2,d=0$
Answer:

It is given that
$\small a=-2,d=0$
Now,
$a_1= a = -2$
$a_2= a_1 + d= -2 + 0 = -2$
$a_3= a_2 + d= -2 + 0 = -2$
$a_4= a_3 + d= -2 + 0 = -2$
Therefore, the first four terms of the given series are -2,-2,-2,-2

Q2 (iii) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=4,d=-3$

Answer:

It is given that
$\small a=4,d=-3$
Now,
$a_1= a =4$
$a_2= a_1 + d= 4 - 3 = 1$
$a_3= a_2 + d= 1 - 3 = -2$
$a_4= a_3 + d= -2- 3 = -5$
Therefore, the first four terms of the given series are 4,1,-2,-5

Q2 (iv) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=-1,d=\frac{1}{2}$

Answer:

It is given that
$\small a=-1,d=\frac{1}{2}$
Now,
$a_1= a =-1$
$a_2= a_1 + d= -1 + \frac{1}{2} = -\frac{1}{2}$
$a_3= a_2 + d= -\frac{1}{2} + \frac{1}{2} = 0$
$a_4= a_3 + d= 0+\frac{1}{2}= \frac{1}{2}$
Therefore, the first four terms of the given series are $-1,-\frac{1}{2},0, \frac{1}{2}$

Q2 (v) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=-1.25,d=-0.25$

Answer:

It is given that
$\small a=-1.25,d=-0.25$
Now,
$a_1= a =-1.25$
$a_2= a_1 + d= -1.25 -0.25= -1.50$
$a_3= a_2 + d= -1.50-0.25=-1.75$
$a_4= a_3 + d= -1.75-0.25=-2$
Therefore, the first four terms of the given series are -1.25,-1.50,-1.75,-2

Q3 (i) For the following APs, write the first term and the common difference: $\small 3,1,-1,-3,...$

Answer:

Given AP series is

$\small 3,1,-1,-3,...$

Now, first term of this AP series is 3

Therefore,

First-term of AP series (a) = 3

Now,

$a_1=3 \ \ and \ \ a_2 = 1$

And common difference (d) = $a_2-a_1 = 1-3 = -2$

Therefore, first term and common difference is 3 and -2 respectively

Q3 (ii) For the following APs, write the first term and the common difference: $\small -5,-1,3,7,...$

Answer:

Given AP series is

$\small -5,-1,3,7,...$

Now, the first term of this AP series is -5

Therefore,

First-term of AP series (a) = -5

Now,

$a_1=-5 \ \ and \ \ a_2 = -1$

And common difference (d) = $a_2-a_1 = -1-(-5) = 4$

Therefore, the first term and the common difference is -5 and 4 respectively

Q3 (iii) For the following APs, write the first term and the common difference: $\small \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},...$

Answer:

Given AP series is

$\small \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},...$
Now, the first term of this AP series is $\frac{1}{3}$

Therefore,

The first term of AP series (a) = $\frac{1}{3}$

Now,

$a_1=\frac{1}{3} \ \ and \ \ a_2 = \frac{5}{3}$

And common difference (d) = $a_2-a_1 = \frac{5}{3}-\frac{1}{3} = \frac{5-1}{3} =\frac{4}{3}$

Therefore, the first term and the common difference is $\frac{1}{3}$ and $\frac{4}{3}$ respectively

Q3 (iv) For the following APs, write the first term and the common difference: $\small 0.6,1.7,2.8,3.9,...$

Answer:

Given AP series is

$\small 0.6,1.7,2.8,3.9,...$

Now, the first term of this AP series is 0.6

Therefore,

First-term of AP series (a) = 0.6

Now,

$a_1=0.6 \ \ and \ \ a_2 = 1.7$

And common difference (d) = $a_2-a_1 = 1.7-0.6 = 1.1$

Therefore, the first term and the common difference is 0.6 and 1.1 respectively.

Q4 (i) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 2,4,8,12,...$

Answer:

Given series is
$\small 2,4,8,12,...$
Now,
the first term to this series is = 2
Now,
$a_1 = 2 \ \ and \ \ a_2 = 4 \ \ and \ \ a_3 = 8$
$a_2-a_1 = 4-2 = 2$
$a_3-a_2 = 8-4 = 4$
We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (ii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 2,\frac{5}{2},3,\frac{7}{2},...$

Answer:

Given series is
$\small 2,\frac{5}{2},3,\frac{7}{2},...$
Now,
first term to this series is = 2
Now,
$a_1 = 2 \ \ and \ \ a_2 = \frac{5}{2} \ \ and \ \ a_3 = 3 \ \ and \ \ a_4 = \frac{7}{2}$
$a_2-a_1 = \frac{5}{2}-2 = \frac{5-4}{2}=\frac{1}{2}$
$a_3-a_2 = 3-\frac{5}{2} = \frac{6-5}{2} = \frac{1}{2}$
$a_4-a_3=\frac{7}{2}-3=\frac{7-6}{2} =\frac{1}{2}$
We can clearly see that the difference between terms are equal and equal to $\frac{1}{2}$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = \frac{7}{2}+\frac{1}{2} = \frac{8}{2}=4$
$a_6=a_5+d = 4+\frac{1}{2} = \frac{8+1}{2}=\frac{9}{2}$
$a_7=a_6+d =\frac{9}{2} +\frac{1}{2} = \frac{10}{2}=5$

Therefore, next three terms of given series are $4,\frac{9}{2} ,5$

Q4 (iii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small -1.2,-3.2,-5.2,-7.2,...$

Answer:

Given series is
$\small -1.2,-3.2,-5.2,-7.2,...$
Now,
the first term to this series is = -1.2
Now,
$a_1 = -1.2 \ \ and \ \ a_2 = -3.2 \ \ and \ \ a_3 = -5.2 \ \ and \ \ a_4 = -7.2$
$a_2-a_1 = -3.2-(-1.2) =-3.2+1.2=-2$
$a_3-a_2 = -5.2-(-3.2) =-5.2+3.2 = -2$
$a_4-a_3=-7.2-(-5.2)=-7.2+5.2=-2$
We can clearly see that the difference between terms are equal and equal to -2
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = -7.2-2 =-9.2$
$a_6=a_5+d = -9.2-2 =-11.2$
$a_7=a_6+d = -11.2-2 =-13.2$
Therefore, next three terms of given series are -9.2,-11.2,-13.2

Q4 (iv) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small -10,-6,-2,2,...$

Answer:

Given series is
$\small -10,-6,-2,2,...$
Now,
the first term to this series is = -10
Now,
$a_1 = -10 \ \ and \ \ a_2 = -6 \ \ and \ \ a_3 = -2 \ \ and \ \ a_4 = 2$
$a_2-a_1 = -6-(-10) =-6+10=4$
$a_3-a_2 = -2-(-6) =-2+6 = 4$
$a_4-a_3=2-(-2)=2+2=4$
We can clearly see that the difference between terms are equal and equal to 4
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 2+4 =6$
$a_6=a_5+d = 6+4=10$
$a_7=a_6+d = 10+4=14$
Therefore, next three terms of given series are 6,10,14

Q4 (v) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...$

Answer:

Given series is
$\small 3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...$
Now,
the first term to this series is = 3
Now,
$a_1 = 3 \ \ and \ \ a_2 = 3+\sqrt2 \ \ and \ \ a_3 = 3+2\sqrt2 \ \ and \ \ a_4 = 3+3\sqrt2$
$a_2-a_1 = 3+\sqrt2-3= \sqrt2$
$a_3-a_2 = 3+2\sqrt2-3-\sqrt2 = \sqrt2$
$a_4-a_3 = 3+3\sqrt2-3-2\sqrt2 = \sqrt2$
We can clearly see that the difference between terms are equal and equal to $\sqrt2$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 3+3\sqrt2+\sqrt2=3+4\sqrt2$
$a_6=a_5+d = 3+4\sqrt2+\sqrt2=3+5\sqrt2$
$a_7=a_6+d = 3+5\sqrt2+\sqrt2=3+6\sqrt2$
Therefore, next three terms of given series are $3+4\sqrt2, 3+5\sqrt2,3+6\sqrt2$

Q4 (vi) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 0.2,0.22,0.222,0.2222,...$

Answer:

Given series is
$\small 0.2,0.22,0.222,0.2222,...$
Now,
the first term to this series is = 0.2
Now,
$a_1 = 0.2 \ \ and \ \ a_2 = 0.22 \ \ and \ \ a_3 = 0.222 \ \ and \ \ a_4 = 0.2222$
$a_2-a_1 = 0.22-0.2=0.02$
$a_3-a_2 = 0.222-0.22=0.002$

We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (vii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 0,-4,-8,-12,...$

Answer:

Given series is
$\small 0,-4,-8,-12,...$
Now,
first term to this series is = 0
Now,
$a_1 = 0 \ \ and \ \ a_2 = -4 \ \ and \ \ a_3 = -8 \ \ and \ \ a_4 = -12$
$a_2-a_1 = -4-0 =-4$
$a_3-a_2 = -8-(-4) =-8+4 = -4$
$a_4-a_3=-12-(-8)=-12+8=-4$
We can clearly see that the difference between terms are equal and equal to -4
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = -12-4 =-16$
$a_6=a_5+d = -16-4=-20$
$a_7=a_6+d = -20-4=-24$
Therefore, the next three terms of given series are -16,-20,-24

Q4 (viii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small -\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},...$

Answer:

Given series is
$\small -\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},...$
Now,
the first term to this series is = $-\frac{1}{2}$
Now,
$a_1 = -\frac{1}{2} \ \ and \ \ a_2 = -\frac{1}{2} \ \ and \ \ a_3 = -\frac{1}{2} \ \ and \ \ a_4 = -\frac{1}{2}$
$a_2-a_1 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
$a_3-a_2 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
$a_4-a_3 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
We can clearly see that the difference between terms are equal and equal to 0
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = -\frac{1}{2}+0=-\frac{1}{2}$
$a_6=a_5+d = -\frac{1}{2}+0=-\frac{1}{2}$
$a_7=a_6+d = -\frac{1}{2}+0=-\frac{1}{2}$
Therefore, the next three terms of given series are $-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}$

Q4 (ix) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 1,3,9,27,...$

Answer:

Given series is
$\small 1,3,9,27,...$
Now,
the first term to this series is = 1
Now,
$a_1 = 1 \ \ and \ \ a_2 = 3 \ \ and \ \ a_3 = 9 \ \ and \ \ a_4 = 27$
$a_2-a_1 = 3-1=2$
$a_3-a_2 =9-3=6$

We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (x) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small a,2a,3a,4a,...$

Answer:

Given series is
$\small a,2a,3a,4a,...$
Now,
the first term to this series is = a
Now,
$a_1 = a \ \ and \ \ a_2 = 2a \ \ and \ \ a_3 = 3a \ \ and \ \ a_4 = 4a$
$a_2-a_1 = 2a-a =a$
$a_3-a_2 = 3a-2a =a$
$a_4-a_3=4a-3a=a$
We can clearly see that the difference between terms are equal and equal to a
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d =4a+a=5a$
$a_6=a_5+d =5a+a=6a$
$a_7=a_6+d =6a+a=7a$
Therefore, next three terms of given series are 5a,6a,7a

Q4 (xi) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small a,a^2,a^3,a^4,...$
Answer:

Given series is
$\small a,a^2,a^3,a^4,...$
Now,
the first term to this series is = a
Now,
$a_1 = a \ \ and \ \ a_2 = a^2 \ \ and \ \ a_3 = a^3 \ \ and \ \ a_4 = a^4$
$a_2-a_1 = a^2-a =a(a-1)$
$a_3-a_2 = a^3-a^2 =a^2(a-1)$

We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small \sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...$

Answer:

Given series is
$\small \sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...$
We can rewrite it as
$\sqrt2,2\sqrt2,3\sqrt2,4\sqrt2,....$
Now,
first term to this series is = a
Now,
$a_1 = \sqrt2 \ \ and \ \ a_2 = 2\sqrt2 \ \ and \ \ a_3 = 3\sqrt2 \ \ and \ \ a_4 = 4\sqrt2$
$a_2-a_1 = 2\sqrt2-\sqrt2 =\sqrt2$
$a_3-a_2 = 3\sqrt2-2\sqrt2 =\sqrt2$
$a_4-a_3=4\sqrt2-3\sqrt2=\sqrt2$
We can clearly see that difference between terms are equal and equal to $\sqrt2$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d =4\sqrt2+\sqrt2=5\sqrt2$
$a_6=a_5+d =5\sqrt2+\sqrt2=6\sqrt2$
$a_7=a_6+d =6\sqrt2+\sqrt2=7\sqrt2$
Therefore, next three terms of given series are $5\sqrt2,6\sqrt2,7\sqrt2$

That is the next three terms are $\sqrt{50},\ \sqrt{72},\ \sqrt{98}$

Q4 (xiii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small \sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...$

Answer:

Given series is
$\small \sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...$
Now,
the first term to this series is = $\sqrt3$
Now,
$a_1 = \sqrt3 \ \ and \ \ a_2 = \sqrt6 \ \ and \ \ a_3 = \sqrt9 \ \ and \ \ a_4 = \sqrt{12}$
$a_2-a_1 = \sqrt6-\sqrt3 =\sqrt3(\sqrt2-1)$
$a_3-a_2 = 3-\sqrt3 =\sqrt3(\sqrt3-1)$
We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xiv) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 1^2,3^2,5^2,7^2,...$

Answer:

Given series is
$\small 1^2,3^2,5^2,7^2,...$
we can rewrite it as
$1,9,25,49,....$
Now,
the first term to this series is = 1
Now,
$a_1 =1 \ \ and \ \ a_2 = 9 \ \ and \ \ a_3 =25 \ \ and \ \ a_4 = 49$
$a_2-a_1 = 9-1 = 8$
$a_3-a_2 = 25-9=16$
We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xv) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 1^2,5^2,7^2,73,...$

Answer:

Given series is
$\small 1^2,5^2,7^2,73,...$
we can rewrite it as
$1,25,49,73....$
Now,
the first term to this series is = 1
Now,
$a_1 =1 \ \ and \ \ a_2 = 25 \ \ and \ \ a_3 =49 \ \ and \ \ a_4 = 73$
$a_2-a_1 = 25-1 = 24$
$a_3-a_2 = 49-25=24$
$a_4-a_3 = 73-49=24$
We can clearly see that the difference between terms are equal and equal to 24
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 73+24=97$
$a_6=a_5+d = 97+24=121$
$a_7=a_6+d = 121+24=145$
Therefore, the next three terms of given series are 97,121,145

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.2

Q1 Fill in the blanks in the following table, given that a is the first term, d the common difference and $\small a_n$ the $\small n$ th term of the AP:

$\small a_n$

(i)

(ii)

(iii)

(iv)

(v)

$\small -18$

$\small ...$

$\small -18.9$

$\small 3.5$

$\small ...$

$\small -3$

$\small 2.5$

$\small ...$

105

$\small ...$

$\small -5$

$\small 3.6$

$\small ...$

Answer:

(i)
It is given that
$a=7, d = 3 , n = 8$
Now, we know that
$a_n = a+(n-1)d$
$a_8 = 7+(8-1)3= 7+7\times 3 = 7+21 = 28$
Therefore,
$a_8 = 28$

(ii) It is given that
$a=-18, n = 10, a_{10} = 0$
Now, we know that
$a_n = a+(n-1)d$
$a_{10} = -18+(10-1)d$
$0 +18=9d$
$d = \frac{18}{9}=2$
(iii) It is given that
$d=-3, n = 18, a_{18} = -5$
Now, we know that
$a_n = a+(n-1)d$
$a_{18} = a+(18-1)(-3)$
$-5=a+17\times (-3)$
$a = 51-5 = 46$
Therefore,
$a = 46$

(iv) It is given that
$a=-18.9, d = 2.5, a_{n} = 3.6$
Now, we know that
$a_n = a+(n-1)d$
$a_{n} = -18.9+(n-1)2.5$
$3.6+18.9= 2.5n-2.5$
$n = \frac{22.5+2.5}{2.5}= \frac{25}{2.5}= 10$
Therefore,
$n = 10$

(v) It is given that
$a=3.5, d = 0, n = 105$
Now, we know that
$a_n = a+(n-1)d$
$a_{105} = 3.5+(105-1)0$
$a_{105} = 3.5$
Therefore,
$a_{105} = 3.5$

Q2 (i) Choose the correct choice in the following and justify: $\small 30$ th term of the AP: $\small 10,7,4,...,$ is

(A) $\small 97$ (B) $\small 77$ (C) $\small -77$ (D) $\small -87$

Answer:

Given series is
$\small 10,7,4,...,$
Here, $a = 10$
and
$d = 7 - 10 = -3$
Now, we know that
$a_n = a+(n-1)d$
It is given that $n = 30$
Therefore,
$a_{30} = 10+(30-1)(-3)$
$a_{30} = 10+(29)(-3)$
$a_{30} = 10-87 = -77$
Therefore, $\small 30$ th term of the AP: $\small 10,7,4,...,$ is -77
Hence, Correct answer is (C)

Q2 (ii) Choose the correct choice in the following and justify : 11th term of the AP: $\small -3,-\frac{1}{2},2,...,$ is

(A) $\small 28$ (B) $\small 22$ (C) $\small -38$ (D) $\small -48\frac{1}{2}$

Answer:

Given series is
$\small -3,-\frac{1}{2},2,...,$
Here, $a = -3$
and
$d =-\frac{1}{2} -(-3)= -\frac{1}{2} + 3 = \frac{-1+6}{2}= \frac{5}{2}$
Now, we know that
$a_n = a+(n-1)d$
It is given that $n = 11$
Therefore,
$a_{11} = -3+(11-1)\left ( \frac{5}{2} \right )$
$a_{11} = -3+(10)\left ( \frac{5}{2} \right )$
$a_{11} = -3+5\times 5 = -3+25 = 22$
Therefore, 11th term of the AP: $\small -3,-\frac{1}{2},2,...,$ is 22
Hence, the Correct answer is (B)

Q3 (i) In the following APs, find the missing terms in the boxes : $\small 2,\hspace {1mm}\fbox{ },\hspace {1mm} 26$

Answer:

Given AP series is
$\small 2,\hspace {1mm}\fbox{ },\hspace {1mm} 26$
Here, $a = 2 , n = 3 \ and \ a_3 = 26$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_3 =2+(3-1)d$
$\Rightarrow 26 -2=(2)d$
$\Rightarrow d = \frac{24}{2}= 12$
Now,
$a_2= a_1+d$
$a_2= 2+12 = 14$
Therefore, the missing term is 14

Q3 (ii) In the following APs, find the missing terms in the boxes: $\small \fbox { },\hspace {1mm}13,\hspace{1mm}\fbox { }, \hspace {1mm} 3$

Answer:

Given AP series is
$\small \fbox { },\hspace {1mm}13,\hspace{1mm}\fbox { }, \hspace {1mm} 3$
Here, $a_2 = 13 , n = 4 \ and \ a_4 = 3$
Now,
$a_2= a_1+d$
$a_1= a = 13 - d$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_4 =13-d+(4-1)d$
$\Rightarrow 3-13=-d+3d$
$\Rightarrow d = -\frac{10}{2}= -5$
Now,
$a_2= a_1+d$
$a_1= a = 13 - d= 13-(-5 ) = 18$
And
$a_3=a_2+d$
$a_3=13-5 = 8$
Therefore, missing terms are 18 and 8
AP series is 18,13,8,3

Q3 (iii) In the following APs, find the missing terms in the boxes : $\small 5,\: \fbox { },\: \fbox { },\: 9\frac{1}{2}$

Answer:

Given AP series is
$\small 5,\: \fbox { },\: \fbox { },\: 9\frac{1}{2}$
Here, $a = 5 , n = 4 \ and \ a_4 = 9\frac{1}{2}= \frac{19}{2}$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_4 =5+(4-1)d$
$\Rightarrow \frac{19}{2} -5=3d$
$\Rightarrow d = \frac{19-10}{2\times 3} = \frac{9}{6} = \frac{3}{2}$
Now,
$a_2= a_1+d$
$a_2 = 5+\frac{3}{2} = \frac{13}{2}$
And
$a_3=a_2+d$
$a_3=\frac{13}{2}+\frac{3}{2} = \frac{16}{2} = 8$
Therefore, missing terms are $\frac{13}{2}$ and 8
AP series is $5,\frac{13}{2}, 8 , \frac{19}{2}$

Q3 (iv) In the following APs, find the missing terms in the boxes : $\small -4,\: \fbox { },\: \fbox { },\: \fbox { },\: \fbox { },\: 6$

Answer:

Given AP series is
$\small -4,\: \fbox { },\: \fbox { },\: \fbox { },\: \fbox { },\: 6$
Here, $a = -4 , n = 6 \ and \ a_6 = 6$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_6 =-4+(6-1)d$
$\Rightarrow 6+4 = 5d$
$\Rightarrow d = \frac{10}{5} = 2$
Now,
$a_2= a_1+d$
$a_2 = -4+2 = -2$
And
$a_3=a_2+d$
$a_3=-2+2 = 0$
And
$a_4 = a_3+d$
$a_4 = 0+2 = 2$
And
$a_5 = a_4 + d$
$a_5 = 2+2 = 4$
Therefore, missing terms are -2,0,2,4
AP series is -4,-2,0,2,4,6

Q3 (v) In the following APs, find the missing terms in the boxes : $\small \fbox { },\: 38,\; \fbox { },\: \fbox { },\: \fbox { },\; -22$

Answer:

Given AP series is
$\small \fbox { },\: 38,\; \fbox { },\: \fbox { },\: \fbox { },\; -22$
Here, $a_2 = 38 , n = 6 \ and \ a_6 = -22$
Now,
$a_2=a_1+d$
$a_1=a =38-d \ \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_6 =38-d+(6-1)d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow -22-38-=-d+5d$
$\Rightarrow d = -\frac{60}{4} = - 15$
Now,
$a_2= a_1+d$
$a_1 = 38-(-15) = 38+15 = 53$
And
$a_3=a_2+d$
$a_3=38-15 = 23$
And
$a_4 = a_3+d$
$a_4 = 23-15 = 8$
And
$a_5 = a_4 + d$
$a_5 =8-15 = -7$
Therefore, missing terms are 53,23,8,-7
AP series is 53,38,23,8,-7,-22

Q4 Which term of the AP : $\small 3,8,13,18,...,$ is $\small 78$ ?
Answer:

Given AP is
$\small 3,8,13,18,...,$
Let suppose that nth term of AP is 78
Here, $a = 3$
And
$d = a_2-a_1 = 8 - 3 = 5$
Now, we know that that
$a_n = a + (n-1)d$
$\Rightarrow 78 = 3 + (n-1)5$
$\Rightarrow 78 -3 = 5n-5$
$\Rightarrow n = \frac{75 +5}{5}= \frac{80}{5} = 16$
Therefore, value of 16th term of given AP is 78

Q5 (i) Find the number of terms in each of the following APs : $\small 7,13,19,...,205$

Answer:

Given AP series is
$\small 7,13,19,...,205$
Let's suppose there are n terms in given AP
Then,
$a = 7 , a_n = 205$
And
$d= a_2-a_1 = 13-7 = 6$
Now, we know that
$a_n =a + (n-1)d$
$\Rightarrow 205=7 + (n-1)6$
$\Rightarrow 205-7 = 6n-6$
$\Rightarrow n = \frac{198+6}{6} = \frac{204}{6} = 34$
Therefore, there are 34 terms in given AP

Q5 (ii) Find the number of terms in each of the following APs : $\small 18,15\frac{1}{2},13,...,-47$

Answer:

Given AP series is
$\small 18,15\frac{1}{2},13,...,-47$
suppose there are n terms in given AP
Then,
$a = 18 , a_n = -47$
And
$d= a_2-a_1 = \frac{31}{2}-18 = \frac{31-36}{2} = -\frac{5}{2}$
Now, we know that
$a_n =a + (n-1)d$
$\Rightarrow -47=18 + (n-1)\left ( -\frac{5}{2} \right )$
$\Rightarrow -47-18= -\frac{5n}{2}+\frac{5}{2}$
$\Rightarrow -\frac{5n}{2}= -65-\frac{5}{2}$
$\Rightarrow -\frac{5n}{2}= -\frac{135}{2}$
$\Rightarrow n = 27$
Therefore, there are 27 terms in given AP

Q6 Check whether $\small -150$ is a term of the AP : $\small 11,8,5,2...$

Answer:

Given AP series is
$\small 11,8,5,2...$
Here, $a = 11$
And
$d = a_2-a_1 = 8-11 = -3$
Now,
suppose -150 is nth term of the given AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow -150 = 11+(n-1)(-3)$
$\Rightarrow -150- 11=-3n+3$
$\Rightarrow =n = \frac{161+3}{3}= \frac{164}{3} = 54.66$
Value of n is not an integer
Therefore, -150 is not a term of AP $\small 11,8,5,2...$

Q7 Find the $\small 31$ st term of an AP whose $\small 11$ th term is $\small 38$ and the $\small 16$ th term is $\small 73$ .

Answer:

It is given that
$\small 11$ th term of an AP is $\small 38$ and the $\small 16$ th term is $\small 73$
Now,
$a_{11} =38= a+ 10d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{16} =73= a+ 15d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= -32 \ \ \ and \ \ \ d = 7$
Now,
$a_{31} = a+30d = -32 + 30\times 7 = -32+210 = 178$
Therefore, 31st terms of given AP is 178

Q8 An AP consists of $\small 50$ terms of which $\small 3$ rd term is $\small 12$ and the last term is $\small 106$ . Find the $\small 29$ th term.
Answer:

It is given that
AP consists of $\small 50$ terms of which $\small 3$ rd term is $\small 12$ and the last term is $\small 106$
Now,
$a_3 = 12=a+2d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{50} = 106=a+49d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 8 \ \ \ and \ \ \ d = 2$
Now,
$a_{29} = a+28d=8+28\times 2 = 8 +56 = 64$
Therefore, 29th term of given AP is 64

Q9 If the $\small 3$ rd and the $\small 9$ th terms of an AP are $\small 4$ and $\small -8$ respectively, which term of this AP is zero?
Answer:

It is given that
$\small 3$ rd and the $\small 9$ th terms of an AP are $\small 4$ and $\small -8$ respectively
Now,
$a_3 = 4=a+2d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{9} = -8=a+8d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 8 \ \ \ and \ \ \ d = -2$
Now,
Let nth term of given AP is 0
Then,
$a_{n} = a+(n-1)d$
$0 = 8+(n-1)(-2)$
$2n = 8+2= 10$
$n = \frac{10}{2} = 5$
Therefore, 5th term of given AP is 0

Q10 The $\small 17$ th term of an AP exceeds its $\small 10$ th term by $\small 7$ . Find the common difference.
Answer:

It is given that
$\small 17$ th term of an AP exceeds its $\small 10$ th term by $\small 7$
i.e.
$a_{17}= a_{10}+7$
$\Rightarrow a+16d = a+9d+7$
$\Rightarrow a+16d - a-9d=7$
$\Rightarrow 7d=7$
$\Rightarrow d = 1$
Therefore, the common difference of AP is 1

Q11 Which term of the AP : $\small 3,15,27,39,...$ will be $\small 132$ more than its $\small 54$ th term?
Answer:

Given AP is
$\small 3,15,27,39,...$
Here, $a= 3$
And
$d= a_2-a_1 = 15 - 3 = 12$
Now, let's suppose nth term of given AP is $\small 132$ more than its $\small 54$ th term
Then,
$a_n= a_{54}+132$
$\Rightarrow a+(n-1)d = a+53d+132$
$\Rightarrow 3+(n-1)12 = 3+53\times 12+132$
$\Rightarrow 12n = 3+636+132+12$
$\Rightarrow 12n = 636+132+12$
$\Rightarrow n = \frac{780}{12}= 65$
Therefore, 65th term of given AP is $\small 132$ more than its $\small 54$ th term

Q12 Two APs have the same common difference. The difference between their $\small 100$ th terms is $\small 100$ , what is the difference between their $\small 1000$ th terms?
Answer:

It is given that
Two APs have the same common difference and difference between their $\small 100$ th terms is $\small 100$
i.e.
$a_{100}-a'_{100}= 100$
Let common difference of both the AP's is d
$\Rightarrow a+99d-a'-99d=100$
$\Rightarrow a-a'=100 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - (i)$
Now, difference between 1000th term is
$a_{1000}-a'_{1000}$
$\Rightarrow a+999d -a'-999d$
$\Rightarrow a-a'$
$\Rightarrow 100 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i) )$
Therefore, difference between 1000th term is 100

Q 13 How many three-digit numbers are divisible by $\small 7$ ?
Answer:

We know that the first three digit number divisible by 7 is 105 and last three-digit number divisible by 7 is 994
Therefore,
$a = 105 , d = 7 \ and \ a_n = 994$
Let there are n three digit numbers divisible by 7
Now, we know that
$a_n = a+ (n-1)d$
$\Rightarrow 994 = 105 + (n-1)7$
$\Rightarrow 7n = 896$
$\Rightarrow n = \frac{896}{7} = 128$
Therefore, there are 128 three-digit numbers divisible by 7

Q14 How many multiples of $\small 4$ lie between $\small 10$ and $\small 250$ ?
Answer:

We know that the first number divisible by 4 between 10 to 250 is 12 and last number divisible by 4 is 248
Therefore,
$a = 12 , d = 4 \ and \ a_n = 248$
Let there are n numbers divisible by 4
Now, we know that
$a_n = a+ (n-1)d$
$\Rightarrow 248 = 12 + (n-1)4$
$\Rightarrow 4n = 240$
$\Rightarrow n = \frac{240}{4} = 60$
Therefore, there are 60 numbers between 10 to 250 that are divisible by 4

Q15 For what value of $\small n$ , are the $\small n$ th terms of two APs: $\small 63,65,67,...$ and $\small 3,10,17,...$ equal?

Answer:

Given two AP's are
$\small 63,65,67,...$ and $\small 3,10,17,...$
Let first term and the common difference of two AP's are a , a' and d , d'
$a = 63 \ , d = a_2-a_1 = 65-63 = 2$
And
$a' = 3 \ , d' = a'_2-a'_1 = 10-3 = 7$
Now,
Let nth term of both the AP's are equal
$a_n = a'_n$
$\Rightarrow a+(n-1)d=a'+(n-1)d'$
$\Rightarrow 63+(n-1)2=3+(n-1)7$
$\Rightarrow 5n=65$
$\Rightarrow n=\frac{65}{5} = 13$
Therefore, the 13th term of both the AP's are equal

Q16 Determine the AP whose third term is $\small 16$ and the $\small 7$ th term exceeds the $\small 5$ th term by $\small 12$ .
Answer:

It is given that
3rd term of AP is $\small 16$ and the $\small 7$ th term exceeds the $\small 5$ th term by $\small 12$
i.e.
$a_3=a+2d = 16 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_7=a_5+12$
$a+6d=a+4d+12$
$2d = 12$
$d = 6$
Put the value of d in equation (i) we will get
$a = 4$
Now, AP with first term = 4 and common difference = 6 is
4,10,16,22,.....

Q17 Find the $\small 20$ th term from the last term of the AP : $\small 3,8,13,...,253$ .

Answer:

Given AP is
$\small 3,8,13,...,253$
Here, $a = 3 \ and \ a_n = 253$
And
$d = a_2-a_1=8-3 = 5$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$253= 3+(n-1)5$
$5n = 255$
$n = 51$
So, there are 51 terms in the given AP and 20th term from the last will be 32th term from the starting
Therefore,
$a_{32} = a+31d$
$a_{32} = 3+31\times 5 = 3+155 = 158$
Therefore, 20th term from the of given AP is 158

Q18 The sum of the $\small 4$ th and $\small 8$ th terms of an AP is $\small 24$ and the sum of the $\small 6$ th and $\small 10$ th terms is $\small 44$ Find the first three terms of the AP.
Answer:

It is given that
sum of the $\small 4$ th and $\small 8$ th terms of an AP is $\small 24$ and the sum of the $\small 6$ th and $\small 10$ th terms is $\small 44$
i.e.
$a_4+a_8=24$
$\Rightarrow a+3d+a+7d=24$
$\Rightarrow 2a+10d=24$
$\Rightarrow a+5d=12 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_6+a_{10}=44$
$\Rightarrow a+5d+a+9d=44$
$\Rightarrow 2a+14d=44$
$\Rightarrow a+7d=22 \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= -13 \ and \ d= 5$
Therefore,first three of AP with a = -13 and d = 5 is
-13,-8,-3

Q19 Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?

Answer:

It is given that
Subba Rao started work at an annual salary of Rs 5000 and received an increment of Rs 200 each year
Therefore, $a = 5000 \ and \ d =200$
Let's suppose after n years his salary will be Rs 7000
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 7000=5000+(n-1)200$
$\Rightarrow 2000=200n-200$
$\Rightarrow 200n=2200$
$\Rightarrow n = 11$
Therefore, after 11years his salary will be Rs 7000
after 11 years, starting from 1995, his salary will reach to 7000, so we have to add 10 in 1995, because these numbers are in years
Thus , 1995+10 = 2005

Q20 Ramkali saved Rs 5 in the first week of a year and then increased her weekly savings by Rs $\small 1.75$ . If in the $\small n$ th week, her weekly savings become Rs $\small 20.75$ , find $\small n$

Answer:

It is given that
Ramkali saved Rs 5 in the first week of a year and then increased her weekly savings by Rs $\small 1.75$
Therefore, $a = 5 \ and \ d = 1.75$
after $\small n$ th week, her weekly savings become Rs $\small 20.75$
Now, we know that
$a_n = a +(n-1)d$
$\Rightarrow 20.75= 5+(n-1)1.75$
$\Rightarrow 15.75= 1.75n-1.75$
$\Rightarrow 1.75n=17.5$
$\Rightarrow n=10$
Therefore, after 10 weeks her saving will become Rs 20.75

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.3

Q1 (i) Find the sum of the following APs: $\small 2,7,12,...,$ to $\small 10$ terms.

Answer:

Given AP is
$\small 2,7,12,...,$ to $\small 10$ terms
Here, $a = 2 \ and \ n = 10$
And
$d = a_2-a_1=7-2=5$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{10}{2}\left \{ 2\times 2 +(10-1)5\right \}$
$\Rightarrow S = 5\left \{ 4 +45\right \}$
$\Rightarrow S = 5\left \{ 49\right \}$
$\Rightarrow S =245$
Therefore, the sum of AP $\small 2,7,12,...,$ to $\small 10$ terms is 245

Q1 (ii) Find the sum of the following APs: $\small -37,-33,-29,...,$ to $\small 12$ terms.

Answer:

Given AP is
$\small -37,-33,-29,...,$ to $\small 12$ terms.
Here, $a = -37 \ and \ n = 12$
And
$d = a_2-a_1=-33-(-37)=4$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{12}{2}\left \{ 2\times (-37) +(12-1)4\right \}$
$\Rightarrow S = 6\left \{ -74 +44\right \}$
$\Rightarrow S = 5\left \{ -30\right \}$
$\Rightarrow S =-180$
Therefore, the sum of AP $\small -37,-33,-29,...,$ to $\small 12$ terms. is -180

Q1 (iii) Find the sum of the following APs: $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms.

Answer:

Given AP is
$\small 0.6,1.7,2.8,...,$ to $\small 100$ terms..
Here, $a = 0.6 \ and \ n = 100$
And
$d = a_2-a_1=1.7-0.6=1.1$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{100}{2}\left \{ 2\times (0.6) +(100-1)(1.1)\right \}$
$\Rightarrow S = 50\left \{ 1.2 +108.9\right \}$
$\Rightarrow S = 50\left \{ 110.1\right \}$
$\Rightarrow S =5505$
Therefore, the sum of AP $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms. is 5505

Q1 (iv) Find the sum of the following APs: $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.

Answer:

Given AP is
$\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.
Here, $a = \frac{1}{15} \ and \ n = 11$
And
$d = a_2-a_1=\frac{1}{12}-\frac{1}{15}= \frac{5-4}{60}= \frac{1}{60}$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{11}{2}\left \{ 2\times \frac{1}{15} +(11-1)(\frac{1}{60})\right \}$
$\Rightarrow S = \frac{11}{2}\left \{ \frac{2}{15} +\frac{1}{6}\right \}$
$\Rightarrow S = \frac{11}{2}\left \{ \frac{9}{30}\right \}$
$\Rightarrow S =\frac{99}{60}= \frac{33}{20}$
Therefore, the sum of AP $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms. is $\frac{33}{20}$

Q2 (i) Find the sums given below : $\small 7+10\frac{1}{2}+14+...+84$

Answer:

Given AP is
$\small 7+10\frac{1}{2}+14+...+84$
We first need to find the number of terms
Here, $a = 7 \ and \ a_n = 84$
And
$d = a_2-a_1=\frac{21}{2}-7= \frac{21-14}{2}= \frac{7}{2}$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 84 = 7 + (n-1)\frac{7}{2}$
$\Rightarrow \frac{7n}{2}= 77+\frac{7}{2}$
$\Rightarrow n = 23$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 2\times7 +(23-1)(\frac{7}{2})\right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 14 +77\right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 91\right \}$
$\Rightarrow S =\frac{2093}{2}=1046\frac{1}{2}$
Therefore, the sum of AP $\small 7+10\frac{1}{2}+14+...+84$ is $1046\frac{1}{2}$

Q2 (ii) Find the sums given below : $\small 34+32+30+...+10$

Answer:

Given AP is
$\small 34+32+30+...+10$
We first need to find the number of terms
Here, $a = 34 \ and \ a_n = 10$
And
$d = a_2-a_1=32-34=-2$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 10 = 34 + (n-1)(-2)$
$\Rightarrow -26 = -2n$
$\Rightarrow n = 13$
Now, we know that
$S = \frac{n}{2}\left \{ a+a_n \right \}$

$\Rightarrow S = \frac{13}{2}\left \{ 44\right \}$
$\Rightarrow S =13\times 22 = 286$
Therefore, the sum of AP $\small 34+32+30+...+10$ is 286

Q2 (iii) Find the sums given below : $\small -5+(-8)+(-11)+...+(-230)$

Answer:

Given AP is
$\small -5+(-8)+(-11)+...+(-230)$
We first need to find the number of terms
Here, $a = -5 \ and \ a_n = -230$
And
$d = a_2-a_1=-8-(-5)= -3$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow -230 = -5 + (n-1)(-3)$
$\Rightarrow -228 = -3n$
$\Rightarrow n = 76$
Now, we know that
$S = \frac{n}{2}\left \{ a+a_n \right \}$
$\Rightarrow S = \frac{76}{2}\left \{ (-5-230 )\right \}$

$\Rightarrow S = 38\left \{ -235\right \}$
$\Rightarrow S = -8930$
Therefore, the sum of AP $\small -5+(-8)+(-11)+...+(-230)$ is -8930

Q3 (i) In an AP: given $\small a=5$ , $\small d=3$ , $\small a_n=50$ , find $\small n$ and $\small S_n$ .

Answer:

It is given that
$a = 5, d = 3 \ and \ a_n = 50$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 50 = 5 + (n-1)3$
$\Rightarrow 48 = 3n$
$\Rightarrow n = 16$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{16}{2}\left \{ 2\times(5) +(16-1)(3)\right \}$
$\Rightarrow S = 8\left \{ 10+45\right \}$
$\Rightarrow S = 8\left \{ 55\right \}$
$\Rightarrow S =440$
Therefore, the sum of the given AP is 440

Q3 (ii) In an AP: given $\small a=7$ , $\small a_1_3=35$ , find $\small d$ and $\small S_1_3$ .

Answer:

It is given that
$a = 7 \ and \ a_{13} = 35$
$a_{13}= a+12d = 35$
$= 12d = 35-7 = 28$
$d = \frac{28}{12}= \frac{7}{3}$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{ 2\times(7) +(13-1)(\frac{7}{3})\right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{14 +28\right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{42\right \}$
$\Rightarrow S_{13} = 13 \times 21 = 273$
Therefore, the sum of given AP is 273

Q3 (iii) In an AP: given $\small a_1_2=37,d=3,$ find $\small a$ and $\small S_1_2$ .

Answer:

It is given that
$d = 3 \ and \ a_{12} = 37$
$a_{12}= a+11d = 37$
$= a= 37-11\times 3 = 37-33=4$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{12} = \frac{12}{2}\left \{ 2\times(4) +(12-1)3\right \}$
$\Rightarrow S_{12} = 6\left \{ 8+33\right \}$
$\Rightarrow S_{12} = 6\left \{41\right \}$
$\Rightarrow S_{12} =246$
Therefore, the sum of given AP is 246

Q3 (iv) In an AP: given $\small a_3=15, S_1_0=125,$ find $\small d$ and $\small S_1_0$
Answer:

It is given that
$\small a_3=15, S_1_0=125$
$a_{3}= a+2d = 15 \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{10} = \frac{10}{2}\left \{ 2\times(a) +(10-1)d\right \}$
$\Rightarrow 125 = 5\left \{ 2a+9d\right \}$
$\Rightarrow 2a+9d = 25 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 17 \ and \ d = -1$
Now,
$a_{10} = a+ 9d = 17 + 9(-1)= 17-9 = 8$
Therefore, the value of d and 10th terms is -1 and 8 respectively

Q3 (v) In an AP: given $\small d=5, S_9=75$ , find $\small a$ and $\small a_9$ .

Answer:

It is given that
$\small d=5, S_9=75$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{9} = \frac{9}{2}\left \{ 2\times(a) +(9-1)5\right \}$
$\Rightarrow 75= \frac{9}{2}\left \{ 2a +40\right \}$
$\Rightarrow 150= 18a+360$
$\Rightarrow a = -\frac{210}{18}=-\frac{35}{3}$
Now,
$a_{9} = a+ 8d = -\frac{35}{3} + 8(5)= -\frac{35}{3}+40 = \frac{-35+120}{3}= \frac{85}{3}$

Q3 (vi) In an AP: given $\small a=2,d=8,S_n=90,$ find $\small n$ and $\small a_n$ .

Answer:

It is given that
$\small a=2,d=8,S_n=90,$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 90 = \frac{n}{2}\left \{ 2\times(2) +(n-1)8\right \}$
$\Rightarrow 180 = n\left \{ 4+8n-8\right \}$
$\Rightarrow 8n^2-4n-180=0$
$\Rightarrow 4(2n^2-n-45)=0$
$\Rightarrow 2n^2-n-45=0$
$\Rightarrow 2n^2-10n+9n-45=0$
$\Rightarrow (n-5)(2n+9)=0$
$\Rightarrow n = 5 \ \ and \ \ n = - \frac{9}{2}$
n can not be negative so the only the value of n is 5
Now,
$a_{5} = a+ 4d = 2+4\times 8 = 2+32 = 34$
Therefore, value of n and nth term is 5 and 34 respectively

Q3 (vii) In an AP: given $\small a=8,a_n=62,S_n=210,$ find $\small n$ and $\small d$ .

Answer:

It is given that
$\small a=8,a_n=62,S_n=210,$
Now, we know that
$a_n = a+(n-1)d$
$62 = 8+(n-1)d$
$(n-1)d= 54 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 210 = \frac{n}{2}\left \{ 2\times(8) +(n-1)d\right \}$
$\Rightarrow 420 = n\left \{ 16+54 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow 420 = n\left \{ 70 \right \}$
$\Rightarrow n = 6$
Now, put this value in (i) we will get
$d = \frac{54}{5}$
Therefore, value of n and d are $6 \ and \ \frac{54}{5}$ respectively

Q3 (viii) In an AP: given $\small a_n=4,d=2,S_n=-14,$ find $\small n$ and $\small a$ .

Answer:

It is given that
$\small a_n=4,d=2,S_n=-14,$
Now, we know that
$a_n = a+(n-1)d$
$4 = a+(n-1)2$
$a+2n = 6\Rightarrow a = 6-2n \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow -14 = \frac{n}{2}\left \{ 2\times(a) +(n-1)2\right \}$
$\Rightarrow -28 = n\left \{ 2(6-2n)+2n-2 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow -28 = n\left \{ 10-2n \right \}$
$\Rightarrow 2n^2-10n-28=0$
$\Rightarrow 2(n^2-5n-14)=0$
$\Rightarrow n^2-7n+2n-14=0$
$\Rightarrow(n+2)(n-7)=0$
$\Rightarrow n = -2 \ \ and \ \ n = 7$
Value of n cannot be negative so the only the value of n is 7
Now, put this value in (i) we will get
a = -8
Therefore, the value of n and a are 7 and -8 respectively

Q3 (ix) In an AP: given $\small a=3,n=8,S=192,$ find $\small d$ .

Answer:

It is given that
$\small a=3,n=8,S=192,$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 192 = \frac{8}{2}\left \{ 2\times(3) +(8-1)d\right \}$
$\Rightarrow 192=4\left \{6 +7d\right \}$
$\Rightarrow 7d = 48-6$
$\Rightarrow d = \frac{42}{7} = 6$
Therefore, the value of d is 6

Q3 (x) In an AP: given $\small l=28,S=144 \ and \ n = 9$ and there are total $\small 9$ terms. Find $\small a$ .

Answer:

It is given that
$\small l=28,S=144 \ and \ n = 9$
Now, we know that
$l = a_n = a+(n-1)d$
$28 = a_n = a+(n-1)d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 144 = \frac{9}{2}\left \{ a + a +(n-1)d\right \}$
$\Rightarrow 288 =9\left \{ a+ 28\right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(using \ (i))$
$\Rightarrow a+28= 32$
$\Rightarrow a=4$
Therefore, the value of a is 4

Q4 How many terms of the AP: $\small 9,17,25,...$ must be taken to give a sum of $\small 636$ ?

Answer:

Given AP is
$\small 9,17,25,...$
Here, $a =9 \ and \ d = 8$
And   $S_n = 636$
Now , we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 636 = \frac{n}{2}\left \{ 18+(n-1)8 \right \}$
$\Rightarrow 1272 = n\left \{ 10+8n \right \}$
$\Rightarrow 8n^2+10n-1272=0$
$\Rightarrow 2(4n^2+5n-636)=0$
$\Rightarrow 4n^2+53n-48n-636=0$
$\Rightarrow (n-12)(4n+53)=0$
$\Rightarrow n = 12 \ \ and \ \ n = - \frac{53}{4}$
Value of n  can not be negative so the only the value of n is 12
Therefore, the sum of 12 terms of AP   $\small 9,17,25,...$ must be taken to give a sum of $\small 636$ .

Q5 The first term of an AP is $\small 5$ , the last term is $\small 45$ and the sum is $\small 400$ . Find the number of terms and the common difference.

Answer:

It is given that
$\small a=5,a_n=45,S_n=400,$
Now, we know that
$a_n = a+(n-1)d$
$45 = 5+(n-1)d$
$(n-1)d= 40 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 400 = \frac{n}{2}\left \{ 2\times(5) +(n-1)d\right \}$
$\Rightarrow 800 = n\left \{ 10+40 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow 800 = n\left \{ 50 \right \}$
$\Rightarrow n = 16$
Now, put this value in (i) we will get
$d = \frac{40}{15}= \frac{8}{3}$
Therefore, value of n and d are $16 \ and \ \frac{8}{3}$ respectively

Q6 The first and the last terms of an AP are $\small 17$ and $\small 350$ respectively. If the common difference is $\small 9$ , how many terms are there and what is their sum?

Answer:

It is given that
$\small a=17,l=350,d=9,$
Now, we know that
$a_n = a+(n-1)d$
$350 = 17+(n-1)9$
$(n-1)9 = 333$
$(n-1)=37$
$n = 38$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{38}= \frac{38}{2}\left \{ 2\times(17) +(38-1)9\right \}$
$\Rightarrow S_{38}= 19\left \{ 34 +333\right \}$
$\Rightarrow S_{38}= 19\left \{367\right \}$
$\Rightarrow S_{38}= 6973$
Therefore, there are 38 terms and their sun is 6973

Q7 Find the sum of first $\small 22$ terms of an AP in which $\small d=7$ and $\small 22$ nd term is $\small 149$ .

Answer:

It is given that
$\small a_{22}=149,d=7,n = 22$
Now, we know that
$a_{22} = a+21d$
$149 = a+21\times 7$
$a = 149 - 147 = 2$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{22}= \frac{22}{2}\left \{ 2\times(2) +(22-1)7\right \}$
$\Rightarrow S_{22}= 11\left \{ 4 +147\right \}$
$\Rightarrow S_{22}= 11\left \{ 151\right \}$
$\Rightarrow S_{22}= 1661$
Therefore, there are 22 terms and their sum is 1661

Q8 Find the sum of first $\small 51$ terms of an AP whose second and third terms are $\small 14$ and $\small 18$ respectively.

Answer:

It is given that
$\small a_{2}=14,a_3=18,n = 51$
And $d= a_3-a_2= 18-14=4$
Now,
$a_2 = a+d$
$a= 14-4 = 10$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 2\times(10) +(51-1)4\right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 20 +200\right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 220\right \}$
$\Rightarrow S_{51}= 51 \times 110$
$\Rightarrow S_{51}=5304$
Therefore, there are 51 terms and their sum is 5610

Q9 If the sum of first $\small 7$ terms of an AP is $\small 49$ and that of $\small 17$ terms is $\small 289$ , find the sum of first $\small n$ terms.

Answer:

It is given that
$S_7 = 49 \ and \ S_{17}= 289$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{7}= \frac{7}{2}\left \{ 2\times(a) +(7-1)d\right \}$
$\Rightarrow 98= 7\left \{ 2a +6d\right \}$
$\Rightarrow a +3d = 7 \ \ \ \ \ \ \ -(i)$
Similarly,
$\Rightarrow S_{17}= \frac{17}{2}\left \{ 2\times(a) +(17-1)d\right \}$
$\Rightarrow 578= 17\left \{ 2a +16d\right \}$
$\Rightarrow a +8d = 17 \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
a = 1 and d = 2
Now, the sum of first n terms is
$S_n = \frac{n}{2}\left \{ 2\times 1 +(n-1)2 \right \}$
$S_n = \frac{n}{2}\left \{ 2 +2n-2 \right \}$
$S_n = n^2$
Therefore, the sum of n terms is $n^2$

Q10 (i) Show that $\small a_1,a_2,...,a_n,...$ form an AP where an is defined as below : $\small a_n=3+4n$ Also find the sum of the first $\small 15$ terms.

Answer:

It is given that
$\small a_n=3+4n$
We will check values of $a_n$ for different values of n
$a_1 = 3+4(1) =3+4= 7$
$a_2 = 3+4(2) =3+8= 11$
$a_3 = 3+4(3) =3+12= 15$
and so on.
From the above, we can clearly see that this is an AP with the first term(a) equals to 7 and common difference (d) equals to 4
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(7) +(15-1)4\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 14 +56\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 70\right \}$
$\Rightarrow S_{15}= 15 \times 35$
$\Rightarrow S_{15}= 525$
Therefore, the sum of 15 terms is 525

Q10 (ii) Show that $\small a_1,a _2,...,a_n,...$ form an AP where an is defined as below : $\small a_n=9-5n$ .Also find the sum of the first $\small 15$ terms in each case.

Answer:

It is given that
$\small a_n=9-5n$
We will check values of $a_n$ for different values of n
$a_1 = 9-5(1) =9-5= 4$
$a_2 = 9-5(2) =9-10= -1$
$a_3 = 9-5(3) =9-15= -6$
and so on.
From the above, we can clearly see that this is an AP with the first term(a) equals to 4 and common difference (d) equals to -5
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(4) +(15-1)(-5)\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 8 -70\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ -62\right \}$
$\Rightarrow S_{15}= 15 \times (-31)$
$\Rightarrow S_{15}= -465$
Therefore, the sum of 15 terms is -465

Q11 If the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$ , what is the first term (that is $\small S_1$ )? What is the sum of first two terms? What is the second term? Similarly, find the $\small 3$ rd, the $\small 10$ th and the $\small n$ th terms

Answer:

It is given that
the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$
Now,
$\Rightarrow S_n = 4n-n^2$
Now, first term is
$\Rightarrow S_1 = 4(1)-1^2=4-1=3$
Therefore, first term is 3
Similarly,
$\Rightarrow S_2 = 4(2)-2^2=8-4=4$
Therefore, sum of first two terms is 4
Now, we know that
$\Rightarrow S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_2 = \frac{2}{2}\left \{ 2\times 3+(2-1)d \right \}$
$\Rightarrow 4 = \left \{6+d \right \}$
$\Rightarrow d = -2$
Now,
$a_2= a+d = 3+(-2 )= 1$
Similarly,
$a_3= a+2d = 3+2(-2 )= 3-4=-1$
$a_{10}= a+9d = 3+9(-2 )= 3-18=-15$
$a_{n}= a+(n-1)d = 3+(n-1)(-2 )= 5-2n$

Q12 Find the sum of the first $\small 40$ positive integers divisible by $\small 6$ .

Answer:

Positive integers divisible by 6 are
6,12,18,...
This is an AP with
$here, \ a = 6 \ and \ d = 6$
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{40}= \frac{40}{2}\left \{ 2\times 6+(40-1)6 \right \}$
$\Rightarrow S_{40}= 20\left \{12+234 \right \}$
$\Rightarrow S_{40}= 20\left \{246 \right \}$
$\Rightarrow S_{40}= 4920$
Therefore, sum of the first $\small 40$ positive integers divisible by $\small 6$ is 4920

Q13 Find the sum of the first $\small 15$ multiples of $\small 8$ .

Answer:

First 15 multiples of 8 are
8,16,24,...
This is an AP with
$here, \ a = 8 \ and \ d = 8$
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times 8+(15-1)8 \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 16+112 \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 128 \right \}$
$\Rightarrow S_{15}= 15 \times 64 = 960$
Therefore, sum of the first 15 multiple of 8 is 960

Q14 Find the sum of the odd numbers between $\small 0$ and $\small 50$ .

Answer:

The odd number between 0 and 50 are
1,3,5,...49
This is an AP with
$here, \ a = 1 \ and \ d = 2$
There are total 25 odd number between 0 and 50
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2\times 1+(25-1)2 \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2+48 \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\times 50$
$\Rightarrow S_{25}= 25 \times 25 = 625$
Therefore, sum of the odd numbers between $\small 0$ and $\small 50$ 625

Q15 A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day, etc., the penalty for each succeeding day being Rs $\small 50$ more than for the preceding day. How much money the contractor has to pay a penalty, if he has delayed the work by $\small 30$ days?

Answer:

It is given that
Penalty for delay of completion beyond a certain date is Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day and penalty for each succeeding day being Rs $\small 50$ more than for the preceding day
We can clearly see that
200,250,300,..... is an AP with
$a = 200 \ and \ d = 50$
Now, the penalty for 30 days is given by the expression
$S_{30}= \frac{30}{2}\left \{ 2\times 200+(30-1)50 \right \}$
$S_{30}= 15\left ( 400+1450 \right )$
$S_{30}= 15 \times 1850$
$S_{30}= 27750$
Therefore, the penalty for 30 days is 27750

Q16 A sum of Rs $\small 700$ is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs $\small 20$ less than its preceding prize, find the value of each of the prizes.

Answer:

It is given that
Each price is decreased by 20 rupees,
Therefore, d = -20 and there are total 7 prizes so n = 7 and sum of prize money is Rs 700 so $S_7 = 700$
Let a be the prize money given to the 1st student
Then,
$S_7 = \frac{7}{2}\left \{ 2a+(7-1)(-20) \right \}$
$700 = \frac{7}{2}\left \{ 2a-120 \right \}$
$2a - 120 = 200$
$a = \frac{320}{2}= 160$
Therefore, the prize given to the first student is Rs 160
Now,
Let $a_2,a_2,...,a_7$ is the prize money given to the next 6 students
then,
$a_2 = a+d = 160+(-20)=160-20=140$
$a_3 = a+2d = 160+2(-20)=160-40=120$
$a_4 = a+3d = 160+3(-20)=160-60=100$
$a_5 = a+4d = 160+4(-20)=160-80=80$
$a_6 = a+5d = 160+5(-20)=160-100=60$
$a_7 = a+6d = 160+6(-20)=160-120=40$
Therefore, prize money given to 1 to 7 student is 160,140,120,100,80,60.40

Q17 In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I???? will plant $\small 1$ tree, a section of Class II will plant $\small 2$ trees and so on till Class XII. There are three sections in each class. How many trees will be planted by the students?

Answer:

First there are 12 classes and each class has 3 sections
Since each section of class 1 will plant 1 tree, so 3 trees will be planted by 3 sections of class 1.Thus every class will plant 3 times the number of their class
Similarly,

No. of trees planted by 3 sections of class 1 = 3

No. of trees planted by 3 sections of class 2 = 6

No. of trees planted by 3 sections of class 3 = 9

No. of trees planted by 3 sections of class 4 = 12
Its clearly an AP with first term(a) = 3 and common difference(d) = 3 and total number of classes(n) = 12

Now, number of trees planted by 12 classes is given by
$S_{12}= \frac{12}{2}\left \{ 2\times 3+(12-1)\times 3 \right \}$
$S_{12}= 6\left ( 6+33 \right )$
$S_{12}= 6 \times 39 = 234$
Therefore, number of trees planted by 12 classes is 234

Q18 A spiral is made up of successive semicircles, with centres alternately at $\small A$ and $\small B$ ??????, starting with centre at $\small A$ , of radii $\small 0.5\hspace {1mm}cm,1.0\hspace {1mm}cm,1.5\hspace {1mm}cm,2.0\hspace {1mm}cm,...$ as shown in Fig. $\small 5.4$ . What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take $\pi =\frac{22}{7}$ )

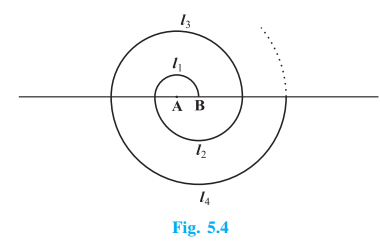
[Hint : Length of successive semicircles is $\small l_1,l_2,l_3,l_4,...$ with centres at $\small A,B,A,B,...,$ respectively.]

Answer:

From the above-given figure

Circumference of 1st semicircle $l_1 = \pi r_1 = 0.5\pi$

Similarly,

Circumference of 2nd semicircle $l_2 = \pi r_2 = \pi$

Circumference of 3rd semicircle $l_3 = \pi r_3 = 1.5\pi$

It is clear that this is an AP with $a = 0.5\pi \ and \ d = 0.5\pi$

Now, sum of length of 13 such semicircles is given by

$S_{13} = \frac{13}{2}\left \{ 2\times 0.5\pi + (13-1)0.5\pi\right \}$
$S_{13} = \frac{13}{2}\left ( \pi+6\pi \right )$
$S_{13} = \frac{13}{2}\times 7\pi$
$S_{13} = \frac{91\pi}{2} = \frac{91}{2}\times \frac{22}{7}=143$
Therefore, sum of length of 13 such semicircles is 143 cm

Q19 $\small 200$ logs are stacked in the following manner: $\small 20$ logs in the bottom row, $\small 19$ in the next row, $\small 18$ in the row next to it and so on (see Fig. $\small 5.5$ ). In how many rows are the $\small 200$ logs placed and how many logs are in the top row?

Answer:

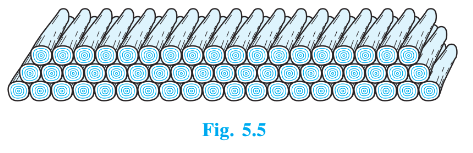
As the rows are going up, the no of logs are decreasing,
We can clearly see that 20, 19, 18, ..., is an AP.
and here $a = 20 \ and \ d = -1$
Let suppose 200 logs are arranged in 'n' rows,
Then,
$S_n = \frac{n}{2}\left \{ 2\times 20 +(n-1)(-1) \right \}$
$200 = \frac{n}{2}\left \{ 41-n \right \}$
$\Rightarrow n^2-41n +400 = 0$
$\Rightarrow n^2-16n-25n +400 = 0$
$\Rightarrow (n-16)(n-25) = 0$
$\Rightarrow n = 16 \ \ and \ \ n = 25$
Now,
case (i) n = 25
$a_{25} =a+24d = 20+24\times (-1)= 20-24=-4$
But number of rows can not be in negative numbers
Therefore, we will reject the value n = 25

case (ii) n = 16
$a_{16} =a+15d = 20+15\times (-1)= 20-15=5$
Therefore, the number of rows in which 200 logs are arranged is equal to 5

Q20 In a potato race, a bucket is placed at the starting point, which is $\small 5$ m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Fig. $\small 5.6$ ).

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

[Hint : To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is $\small 2\times5+2\times (5+3)$ ]

Answer:

Distance travelled by the competitor in picking and dropping 1st potato $= 2 \times 5 = 10 \ m$

Distance travelled by the competitor in picking and dropping 2nd potato $= 2 \times (5+3) =2\times 8 = 16 \ m$

Distance travelled by the competitor in picking and dropping 3rd potato $= 2 \times (5+3+3) =2\times 11 = 22 \ m$

and so on
we can clearly see that it is an AP with first term (a) = 10 and common difference(d) = 6
There are 10 potatoes in the line
Therefore, total distance travelled by the competitor in picking and dropping potatoes is
$S_{10}= \frac{10}{2}\left \{ 2\times 10+(10-1)6 \right \}$
$S_{10}= 5\left ( 20+54 \right )$
$S_{10}= 5\times 74 = 370$

Therefore, the total distance travelled by the competitor in picking and dropping potatoes is 370 m

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.4

Q1 Which term of the AP: is its first negative term? [Hint : Find $n$ for $a_n<0$ ]

Answer:

Given AP is
$\small 121,117,113,...,$
Here $a = 121 \ and \ d = -4$
Let suppose nth term of the AP is first negative term
Then,
$a_n = a+ (n-1)d$
If nth term is negative then $a_n < 0$
$\Rightarrow 121+(n-1)(-4) < 0$
$\Rightarrow 125<4n$
$\Rightarrow n > \frac{125}{4}=31.25$
Therefore, first negative term must be 32nd term

Q2 The sum of the third and the seventh terms of an AP is $\small 6$ and their product is $\small 8$ . Find the sum of first sixteen terms of the AP.

Answer:

It is given that sum of third and seventh terms of an AP are and their product is $\small 8$
$a_3= a+ 2d$
$a_7= a+ 6d$
Now,
$a_3+a_7= a+ 2d+a+6d= 6$
$\Rightarrow 2a+8d = 6$
$\Rightarrow a+4d = 3 \Rightarrow a = 3-4d \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_3.a_7 = (a+2d).(a+6d)=a^2+8ad +12d^2 = 8 \ \ \ \ \ \ \ -(ii)$
put value from equation (i) in (ii) we will get
$\Rightarrow (3-4d)^2+8(3-4d)d+12d^2= 8$
$\Rightarrow 9+16d^2-24d+24d-32d^2+12d^2=8$
$\Rightarrow 4d^2 = 1$
$\Rightarrow d = \pm \frac{1}{2}$
Now,
case (i) $d = \frac{1}{2}$

$a= 3 - 4 \times \frac{1}{2} = 1$
Then,
$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\frac{1}{2} \right \}$

$S_{16}=76$

case (ii) $d = -\frac{1}{2}$
$a= 3 - 4 \times \left ( -\frac{1}{2} \right ) = 5$
Then,
$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\left ( -\frac{1}{2} \right ) \right \}$

$S_{16}=20$

Q3 A ladder has rungs $\small 25$ cm apart. (see Fig. $\small 5.7$ ). The rungs decrease uniformly in length from $\small 45$ cm at the bottom to $\small 25$ cm at the top. If the top and the bottom rungs are $\small 2\frac{1}{2}$ m apart, what is the length of the wood required for the rungs? [Hint: Number of rungs $=\frac{250}{25}+1]$

Answer:

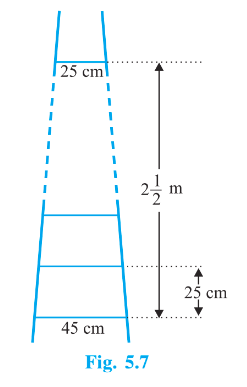
It is given that
The total distance between the top and bottom rung $= 2\frac{1}{2}\ m = 250cm$
Distance between any two rungs = 25 cm
Total number of rungs = $\frac{250}{25}+1= 11$
And it is also given that bottom-most rungs is of 45 cm length and topmost is of 25 cm length.As it is given that the length of rungs decrease uniformly, it will form an AP with $a = 25 , a_{11} = 45 \ and \ n = 11$
Now, we know that
$a_{11}= a+ 10d$

$\Rightarrow 45=25+10d$
$\Rightarrow d = 2$
Now, total length of the wood required for the rungs is equal to
$S_{11} = \frac{11}{2}\left \{ 2\times 25+(11-1)2 \right \}$
$S_{11} = \frac{11}{2}\left \{ 50+20 \right \}$
$S_{11} = \frac{11}{2}\times 70$
$S_{11} =385 \ cm$
Therefore, the total length of the wood required for the rungs is equal to 385 cm

Q4 The houses of a row are numbered consecutively from $\small 1$ to $\small 49$ . Show that there is a value of $\small x$ such that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the houses following it. Find this value of $\small x$ . [Hint : $\small S_{x-1}=S_4_9-S_x$ ]

Answer:

It is given that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the houses following it
And 1,2,3,.....,49 form an AP with a = 1 and d = 1
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
Suppose their exist an n term such that ( n < 49)
Now, according to given conditions
Sum of first n - 1 terms of AP = Sum of terms following the nth term
Sum of first n - 1 term of AP = Sum of whole AP - Sum of first m terms of AP
i.e.
$S_{n-1}=S_{49}-S_n$

$\frac{n-1}{2}\left \{ 2a+((n-1)-1)d \right \}=\frac{49}{2}\left \{ 2a+(49-1)d \right \}-\frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\frac{n-1}{2}\left \{ 2+(n-2) \right \}=\frac{49}{2}\left \{ 2+48 \right \}-\frac{n}{2}\left \{ 2+(n-1) \right \}$

$\frac{n-1}{2}\left \{ n\right \}=\frac{49}{2}\left \{ 50 \right \}-\frac{n}{2}\left \{ n+1 \right \}$

$\frac{n^2}{2}-\frac{n}{2}=1225-\frac{n^2}{2}-\frac{n}{2}$

$n^2 = 1225$
$n = \pm 35$

Given House number are not negative so we reject n = -35

Therefore, the sum of no of houses preceding the house no 35 is equal to the sum of no of houses following the house no 35

Q5 A small terrace at a football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and built of solid concrete. Each step has a rise of $\small \frac{1}{4}\: m$ and a tread of $\small \frac{1}{2}\: m$ . (see Fig. $\small 5.8$ ). Calculate the total volume of concrete required to build the terrace.
[Hint: Volume of concrete required to build the first step $\small =\frac{1}{4}\times \frac{1}{2}\times 50\: m^3$ ]

Answer:

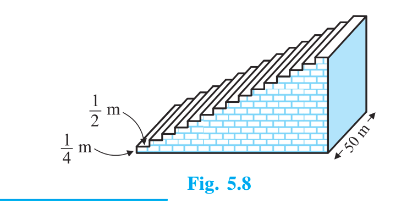
It is given that
football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and Each step has a rise of $\small \frac{1}{4}\: m$ and a tread of $\small \frac{1}{2}\: m$
Now,
The volume required to make the first step = $\frac{1}{4}\times \frac{1}{2}\times 50 = 6.25 \ m^3$

Similarly,

The volume required to make 2nd step = $\left ( \frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{1}{2}\times \frac{1}{2}\times 50 = 12.5 \ m^3$
And
The volume required to make 3rd step = $\left ( \frac{1}{4}+\frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{3}{4}\times \frac{1}{2}\times 50 = 18.75 \ m^3$

And so on
We can clearly see that this is an AP with $a= 6.25 \ and \ d = 6.25$
Now, the total volume of concrete required to build the terrace of 15 such step is
$S_{15} =\frac{15}{2}\left \{ 2 \times 6.25 +(15-1)6.25 \right \}$
$S_{15} =\frac{15}{2}\left \{ 12.5 +87.5\right \}$
$S_{15} =\frac{15}{2}\times 100$
$S_{15} =15\times 50 = 750$
Therefore, the total volume of concrete required to build the terrace of 15 such steps is $750 \ m^3$

Chapter No.	Chapter Name
Chapter 1	CBSE NCERT solutions for class 10 maths chapter 1 Real Numbers
Chapter 2	NCERT solutions for class 10 maths chapter 2 Polynomials
Chapter 3	Solutions of NCERT class 10 maths chapter 3 Pair of Linear Equations in Two Variables
Chapter 4	CBSE NCERT solutions for class 10 maths chapter 4 Quadratic Equations
Chapter 5	NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions
Chapter 6	Solutions of NCERT class 10 maths chapter 6 Triangles
Chapter 7	CBSE NCERT solutions for class 10 maths chapter 7 Coordinate Geometry
Chapter 8	NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry
Chapter 9	Solutions of NCERT class 10 maths chapter 9 Some Applications of Trigonometry
Chapter 10	CBSE NCERT solutions class 10 maths chapter 10 Circles
Chapter 11	NCERT solutions for class 10 maths chapter 11 Constructions
Chapter 12	Solutions of NCERT class 10 chapter maths chapter 12 Areas Related to Circles
Chapter 13	CBSE NCERT solutions class 10 maths chapter 13 Surface Areas and Volumes
Chapter 14	NCERT solutions for class 10 maths chapter 14 Statistics
Chapter 15	Solutions of NCERT class 10 maths chapter 15 Probability

Exams

Colleges

Predictors

Resources

Quick links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Predictor

Resources

Exams

Predictors

Resources

Upcoming Events

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Country

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors

Resources

Engineering Preparation

Government Jobs

Medical Preparation

NCERT Solutions

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors

Exams

Predictors

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.1

Answer:

Answer:

Answer:

Answer:

Answer:

Q2 (ii) Write first four terms of the AP when the first term a and the common difference d are given as follows: Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Q2 (ii) Write first four terms of the AP when the first term a and the common difference d are given as follows: $\small a=-2,d=0$
Answer:

Q3 (iv) In the following APs, find the missing terms in the boxes : $\small -4,\: \fbox { },\: \fbox { },\: \fbox { },\: \fbox { },\: 6$