Apply to Aakash iACST Scholarship Test 2024
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State - As we know that there are three states of matter which are solid, liquid, and gas but in the NCERT solutions for Class 12 Chemistry chapter 1, you will only get to know the solutions to Solid State. These NCERT solutions are prepared by Careers360 subject experts keeping in my of latest CBSE syllabus 2023 in simple and step by step comprehensive coverage.
Latest: JEE Main high scoring chapters
Don't Miss: JEE Main 10 year's papers
Recommended: NEET high scoring chapters
Suggested: NEET question papers with solutions
In this chapter of NCERT book, you will be introduced to different types of structure of solids which exist in nature. For eg., NaCl has a cubic structure and Graphite has Hexagonal structure. At the end of the NCERT solutions for Class 12 Chemistry Chapter 1, you will also get to know the defects in these solid structures. By referring to the NCERT solutions for class 12, students can understand all the important concepts and practice questions well enough before their examination.
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State
Solutions to In-Text questions Ex 1.1 to 1.24
Q 1.1 Why are solids rigid?
Answer :
Solids have good intermolecular force of attraction, which tend to keep molecules of solid closer. And thus make solid rigid.
Q 1.2 Why do solids have a definite volume?
Answer :
At room temperature, intermolecular forces bring molecules so close that they cling to one another and occupy fixed positions. They oscillate about their mean position but they have fixed volume. So, due to the fixed position of particles and strong intermolecular force, solids have a definite volume.
Q 1.3(i) Classify the following as amorphous or crystalline solids: Polyurethane
Answer :
Polyurethane is an amorphous solid.
Q 1.3(ii) Classify the following as amorphous or crystalline solids:
Answer :
Naphthalene is a crystalline solids.
Q 1.3(iii) Classify the following as amorphous or crystalline solids: benzoic acid,
Answer :
Benzoic acid is a crystalline solid.
Q 1.3(iv) Classify the following as amorphous or crystalline solids:
Answer :
Teflon is an amorphous solid.
Q 1.3(v) Classify the following as amorphous or crystalline solids:
Answer :
Potassium nitrate is a crystalline solid.
Q 1.3(vi) Classify the following as amorphous or crystalline solids:
Answer :
Cellophane is an amorphous solid.
Q 1.3(vii) Classify the following as amorphous or crystalline solids:
Answer :
Polyvinyl chloride is an amorphous solid.
Q 1.3(viii) Classify the following as amorphous or crystalline solids:
Answer :
Fibre glass is an amorphous solid.
Q 1.3(ix) Classify the following as amorphous or crystalline solids:
Answer :
Copper is a crystalline solid.
Q 1.4 Why is glass considered a super cooled liquid?
Answer: Glass is an amorphous solid. Just like liquids, amorphous solids also have a tendency to flow, though very slowly. Therefore, these are called pseudo solids or supercooled liquids.
Answer :
We know that amorphous solid are isotropic in nature i.e., their properties are same in all directions. According to given description, the nature of given solid is amorphous.
Clevage property :- When we cut the solid with a sharp edged tool, they cut into two pieces with irregular surfaces.
Question 1.6(i) Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Answer :
Potassium sulphate is an ionic solid.
Answer :
Tin is a metallic solid.
Answer :
Benzene is a covalent molecule but a molecular solid because its molecules are together by the intermolecular force of attraction.
Answer :
Urea is a molecular solid (Polar).
Answer :
Ammonia is a molecular solid (Polar).
Answer :
Water is a molecular solid having hydrogen bonds.
Answer :
Zinc sulphide is an ionic solid.
Answer :
Graphite is made up of carbon atoms covalently bonded with each other.
So graphite is a covalent solid or network solid.
Answer :
Rubidium is a metallic solid.
Answer :
Argon is an inert gas so it is non-polar molecular solid.
Answer :
Silicon carbide is a covalent solid.
Answer :
As per the given properties, Solid A shows the absence of ionic properties in it. A is a covalent or network solid (exception graphite, which is soft and conductor of electricity).
Q 1.8 Ionic solids conduct electricity in molten state but not in solid-state. Explain.
Answer :
In the solid state, the ions are not free to move about so they are electrical insulators. But, in the molten state or when ionic solids are dissolved in water, the ions become free to move about so they conduct electricity.
Q 1.9 What type of solids are electrical conductors, malleable and ductile?
Answer :
Metallic solids are hard but malleable and ductile. Also, they are conductors in solid as well as in the molten state.
Q 1.10 Give the significance of a ‘lattice point’.
Answer :
A crystal lattice is the pattern of points representing the locations of motifs. And each point in a lattice is called lattice points. These points are significant as they represent one constituent particle which may be an atom, a molecule (a group of atoms) or an ion.
Q 1.11 Name the parameters that characterise a unit cell.
Answer :
A unit cell is characterised by:-
(i) its dimensions along the three edges a, b and c. These edges may or may not be mutually perpendicular.
(ii) angles between the edges, α (between b and c), β (between a and c) and γ (between a and b). Thus, a unit cell is characterised by six parameters
a, b, c, α, β and γ.
Q 1.12 Distinguish between
(i) Hexagonal and monoclinic unit cells
(ii) Face-centred and end-centred unit cells .
Answer :
(i) Hexagonal and monoclinic unit cells:-
| Properties | Hexagonal | Monoclinic |
| Possible Variation | Primitive | Primitive, End centered |
| Axial distance | ||
| Axial angles | ||
| Examples | Graphite, ZnO | Monoclinic sulphur |
(ii) Face-centred and end-centred unit cells: -
- A face-centred unit cell contains atoms at all the corners and at the centre of all the faces, whereas in end - centred unit cell one pair of opposite faces contains atoms apart from atoms at all the corners.
- The total number of atoms in a unit cell differs by 1.
Q 1.13 Explain how much portion of an atom located at
(i) corner and
(ii) bodycentre of a cubic unit cell is part of its neighbouring unit cell.
Answer :
(i) At corner:- Each atom at a corner is shared between eight adjacent unit cells, four unit cells in the same layer and four unit cells of the upper (or lower) layer. Therefore, only of an atom (or molecule or ion) actually belongs to a particular unit cell.
(ii) At body centre of cubic cell :- Since body centre atom completely belongs to the unit cell in which it is present, thus it is not part of any neighbouring unit cell. So, one atom belongs to a one unit cell.
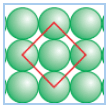
Q 1.14 What is the two dimensional coordination number of a molecule in square close-packed layer?
Answer :
In two dimensional square closed packed layer, one atom is in contact with 4 of its neighbouring atoms. So its cordination number is 4.
![]()
Answer :
Amount of compound given = 0.5 mol
We know that,
So, No. of atoms
We also know that, No. of tetrahedral voids = 2(No. of atoms in closed packing)
No. of octahedral voids = No. of atoms present in closed packing.
So, Total number of voids = No. of tetrahedral voids + No. of octahedral voids.
Answer :
It is given that element N forms CCP.
Let us assume, the number of atoms of element N (which forms ccp) is x.
Then no. of tetrahedral voids = 2x.
It is also given that M occupies of tetrahedral voids.
So the number of atoms of element M :
So the molecular formula bocomes : 2
3 .
Q 1.17 Which of the following lattices has the highest packing efficiency
(i) simple cubic
(ii) body-centred cubic and
(iii) hexagonal close-packed lattice?
Answer :
(i) Simple cubic:- In a simple cubic lattice the atoms are located only on the corners of the cube.
Thus, the edge length or side of the cube ‘a’, and the radius of each particle, r are related as a = 2r
Volume of cubic unit cell = =
And Volume of 1 atom :
(ii) Body centred cubic:- In body centred cubic, we have atoms at all corners and at body centre.
Clearly, the atom at the centre will be in touch with the other two atoms diagonally arranged.
; and
Also, the length of body diagonal is equal to 4r.
The volume of the cube :
In BCC, a total number of atoms is 2.
(iii) Hexagonal close-packed:- We know that both types of (hcp and ccp) are equally efficient. We also know that the packing efficiency of ccp is 74 percent.
(i) Simple cubic = 52.4%
(ii) Body centred cubic=68%
(iii) Hexagonal close-packed=74%
Thus among all, packing efficiency of hcp is the highest.
Answer :
We know that :
We are given :
and
and
So we need to find z (no. of atoms present in unit cell) by putting all values in formula of density.
We get, .
It is known that face centred cubic also has 4 atoms in its unit cell, So given cubic unit cell is face centred.
Answer :
When a solid is heated some of the atoms moves out due to increase in its thermal energy. This leads to a vacancy defect. Affected physical property:- Since some of the atoms moved out so its density decreases.
Q 1.20(i) What type of stoichiometric defect is shown by:
Answer :
ZnS shows frenkel defect example because there is a large difference in the size of Zn and S.
Q 1.20(ii) What type of stoichiometric defect is shown by:
Answer :
AgBr shows both, Frenkel as well as Schottky defects.
Answer :
In impurity defect, the higher valency cation replaces the lower valency cation. An important point to be noted is that electrical neutrality is maintained.
For e.g. In case of NaCl and SrCl 2 , some of the sites of Na + ions are occupied by Sr 2+ . Two Na + ions are replaced by Sr +2 ions. It occupies the site of one ion and the other site remains vacant. The cationic vacancies thus produced are equal in number to that of Sr 2+ ions.
Answer :
In metal excess defect F-centres are generated. F-centres are the anionic sites occupied by unpaired electrons. These F-centres are responsible for the developing of colour.
For e.g. when crystals of KCl are heated in an atmosphere of sodium vapour, the potassium atoms comes on the surface of the KCl. Then the Cl– ions go to the surface of the KCl and get combined with K atoms to give KCl. This happens by loss of an electron by potassium atoms to form K + ions. The released electrons during the process go into the KCl and occupy anionic sites. Thus the crystal now has an excess of potassium. Generation of F-centres takes place. They impart violet colour to the crystals of KCl.
Answer :
The 14 group elements have four valence electrons, whereas group 15 elements like P have 5 valence electrons. In this, 4 out of 5 are used in making a bond with group 14 element and 1 is extra and becomes delocalised. This result in extra conductivity. So group 14 elements are required to be doped with the group 15 elements for forming n-type conductors.
Answer :
Substances like iron, cobalt (Ferromagnetic) can make better permanent magnets because in the solid state these substances are grouped together in small regions called domains. Each domain acts like a tiny magnet. They are randomly arranged when placed in the unmagnetised state. But when they are placed in magnetic field domains align in direction of the magnetic field. But in case of ferrimagnetic materials domains are aligned in parallel and anti-parallel direction, which lead to loss of total magnetic effect.
Q 1.1 Define the term 'amorphous'. Give a few examples of amorphous solids.
Answer :
Amorphous solids have the constituent particles arranged only in short-range order and consequently, they behave like supercooled liquids. So do not have sharp melting points. Also, they are isotropic in nature i.e., their physical properties are the same in all directions.
E.g. quartz glass, polymers, gels etc.
Answer :
The arrangement of constituent particles makes glass different from quartz. In glass short-range order of particles exists whereas in quartz long range of particles is seen. Glass is an amorphous solid while quartz is a crystalline form of silica.
Quartz can be converted into glass by heating it strongly till it comes to a molten state and then cooling it rapidly so that it does not get time to crystallize.
Tetra phosphorus decoxide (P 4 O 10 )
Answer :
Tetra phosphorus decoxide (P 4 O 10 ) is a molecular solid.
Ammonium phosphate (NH 4 ) 3 PO 4
Answer :
(ii) Ammonium phosphate (NH 4 ) 3 PO 4 :- It is an ionic solid.
Answer:
(iii) :- It is a covalent or network solid.
Answer:
(iv) I 2 :-It is a molecular solid.
Answer :
(v) P 4 :- It is a molecular solid.
Answer :
(vi) Plastic :- Plastic is an amorphous solid.
Answer :
(vii) Graphite :- It is a covalent or network solid.
Q 1.3(viii) Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous.
Answer :
(viii) Brass :- It is a metallic solid.
Answer :
(ix) Rb :- It is a metallic solid.
Answer :
(x) LiBr :- It is an ionic solid.
Answer :
(xi) Si :- It is a network or covalent solid.
Q 1.4(i) What is meant by the term 'coordination number'?
Answer :
Coordination number is defined as the number of the nearest neighbours of a particle.
Q 1.4(ii) What is the coordination number of atoms:
(a) in a cubic close-packed structure?
(b) in a body-centred cubic structure?
Answer :
(i) In ccp coordination number is 12.
(ii) Coordination number of atoms in bcc is 8.
Answer :
We know that density is related to molar mass and edge length by the formula :
where, d= Density
a 3 = The volume of the unit cell
M= Atomic mass
Z = No. of atoms in unit cell
N a = Avogadro’s number.
Answer :
If a crystal has a high melting point implies that it will require high temperature or say energy to break the intermolecular bonds. Also if the intermolecular forces are strong then the crystal is more stable. Thus it can be said that higher the melting point high is the stability.
Melting points of compounds are given below:-
(i) Water:- 273 K
(ii) Ethyl alcohol:- 155.7 K
(iii) Diethyl ether:- 156.8 K
(iv) Methane:- 90.5 K
It can be concluded from the above data that among all, the intermolecular force of attraction is highest in water and lowest in methane. The possible reason for this is the hydrogen bonding present in water whereas the Vanderwall force of attraction is present in case of methane.
Q 1.7(i) How will you distinguish between the following pairs of terms:
Hexagonal close-packing and cubic close-packing?
Answer :
(i) Hexagonal close-packing:- In this, tetrahedral voids of the second layer are covered by the spheres of the third layer. In this case, the atoms (spheres) of the third layer are aligned with those of the first layer. This results in the pattern of spheres to be repeated in alternate layers. We get a pattern as ABAB ....... . This structure is known as the hexagonal close-packed (hcp) structure.
(ii) Cubic close-packing:- In this case, the third layer is placed above the second layer such that its spheres cover the octahedral voids. In this manner, the atoms (spheres) of the third layer are not aligned with those of either the first or the second layer. This pattern of layers is written as ABCABC ........... . This structure is called cubic close-packed (ccp)
Q 1.7(ii) How will you distinguish between the following pairs of terms:
Crystal lattice and unit cell?
Answer :
(i) Crystal lattice:- Crystal lattice is a three-dimensional array of points. The crystal structure is generated by using structural motifs with lattice points.Each point in a crystal lattice denotes one constituent particle which can be either an atom, a molecule (a group of atoms).
(ii) Unit cell:- It is the smallest unit of a crystal lattice which when repeated gives the crystal structure.
Q 1.7(iii) How will you distinguish between the following pairs of terms:
Tetrahedral void and octahedral void?
Answer :
(iii) Tetrahedral void:- When a sphere (atom) of the second layer is above the void of the first layer (or vice versa) production of a tetrahedral void takes place. These voids are known as tetrahedral voids as, when the centres of these four spheres are joined a tetrahedron is formed.
(iv) Octahedral void:- The voids having a triangular in shape (or triangular voids) in the second layer are above the triangular voids in the first layer, also the triangular shapes of these do not overlap. One of them has the apex of the triangle pointing upwards and the other downwards. These voids are surrounded by six spheres/atoms and called as octahedral voids.
Q 1.8(i) How many lattice points are there in one unit cell of each of the following lattice?
Face-centred cubic
Answer :
In face centred cubic atoms are present at all 8 corners and at the centre of each face (6 faces in one unit cell). So total no. of lattice points are 14.
Q 1.8(ii) How many lattice points are there in one unit cell of each of the following lattice?
Face-centred tetragonal
Answer :
In face centred tetragonal atoms are present at all 8 corners and at centre of each face (total 6 faces).
So total lattice points are 14.
Q 1.8(iii) How many lattice points are there in one unit cell of each of the following lattice?
Body-centred
Answer :
In body centred atoms are present at all 8 corners and 1 atom is present at body centre. So total number of lattice points are 9 in bcc .
Q 1.9(i) Explain,
The basis of similarities and differences between metallic and ionic crystals.
Answer :
Similarities:- Both ionic and metallic crystals are hard in nature due to the good force of attraction between molecules. Both have fairly high melting points. In both ionic and metallic bond is non-directional.
Differences:- In ionic solids, attractive forces are coulombic or electrostatic whereas in case of metallic solids forces attractive forces are metallic bonding.
Moreover, ionic solids are insulators in the solid state whereas metallic solids are a very good conductor of electricity in both solid and molten state.
Q 1.10(i) Calculate the efficiency of packing in case of a metal crystal for
Answer:
(i) Simple cubic :- In a simple cubic lattice the atoms are located only on the corners of the cube.
Thus, the side of the cube ‘a’, and the radius of each particle, r are related as:
a = 2r
Volume of cubic unit cell = =

And Volume of 1 atom :
Thus packing efficiency of simple cubic is
Q 1.10(ii) Calculate the efficiency of packing in case of a metal crystal for
body-centred cubic
Answer:
(ii) Body centred cubic:- In body centred cubic, we have atoms at all corners and at body centre.
Clearly, the atom at the centre will be in touch with the other two atoms diagonally arranged.
; and

Also the length of body diagonal is equal to 4r.
Thus,
The volume of a cube :
In BCC, the total number of atoms is 2.
Q 1.10(iii) Calculate the efficiency of packing in case of a metal crystal for
face-centred cubic (with the assumptions that atoms are touching each other).
Answer:
In fcc, we know that we have a total of 4 efficient atoms present.
Also, radius and edge length of the sphere can be related by the following relation :
The above relation can be found out by equating diagonal of 1 face to 4r. (2r from the atom at face centre and r from each atom at a corner.)
Thus packing efficiency becomes:-
Answer :
The relation between density, molar mass and edge length is given by:-
It is given that silver crystallises in fcc lattice, so the value of z = 4. (since it is known that 4 atoms are completely efficient in fcc lattice)
Convert these into SI units,
Answer:
It is given that element Q is at corners of the cube.
So total atoms of element Q per unit cell = 1
And it is also given that element P is present at body centre.
So the total number of atoms of element P per unit cell = 1.
Therefore formula of the compound becomes: PQ
It is clear that it is a bcc lattice so coordination number of P and Q is 8.
Answer :
Here we will use the relation between density and edge length.
It is given that Niobium crystallises in body-centred cubic structure so the value of z = 2.
So we will put the value of density, molar mass and z.
We get,
or
or
We know the relation between the radius of the atom and edge length in bcc lattice.
we get the radius of niobium atom = 143.1 pm.
Answer:
From the figure, it is clear that we can use Pythagoras theorem and find the relation between R and r. 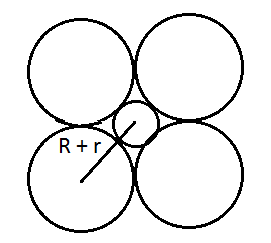
Using pythagoreas theorem :
or
or
or
Answer :
The relation between density and edge lenght gives :
Since it crystallises in fcc lattice, thus z = 4.
Molar mass of copper = 63.546 u.
So,
Q 1.16 Analysis shows that nickel oxide has the formula What fractions of nickel exist as
and
Answer :
Given formula is Ni 0.98 O 1.00 .
Ratio of Ni to O is 0.98.
This means 98 Ni are required for 100 atoms of O.
Let us assume that Ni +2 ions are x.
So the number of Ni +3 ions will be 98 - x.
Using the charge neutrality principle, the net charge of Ni should be equal to a net charge of O.
So the equation becomes :
x(2) + (98-x)3 = 2(100)
or 2x + 294 - 3x = 200
or x = 94.
Thus the fraction of Ni +2 ions =
and fraction of Ni +3 ions = 4%
fraction of Ni +2 ions = 100-4 =96%
Answer :
Semiconductors are the solids with have conductivities in the range from to
. In the case of semiconductors, the gap between the valence band and the conduction band is small. Thus, some electrons may jump to the conduction band and may show some conductivity.
Based on the doping process we have two types of semiconductors.
(i) n-type semiconductors:- In the case of n-type semiconductor doping is done by using group 15 elements like P(have 5 valence electrons).
Group 14 elements have 4 valence electrons; these all 4 valence electrons are bonded with 4 valence electron of group 15 element. One left out electron delocalised and increases the conductivity. Due to the presence of one extra electron, it is also called as electron-rich impurities.
(ii) p-type semiconductors:- In the case of p-type semiconductors we use group 13 impurities such as Al (having 3 valence electrons). This results in the generation of electron hole due to the missing electron in 4th place. From a neighbouring atom, an electron can come and fill the electron-hole, but it will then create a new electron-hole at the position from where electron moved. In this circumstance, it would appear as if the electron-hole is moving in the direction opposite to that of the electron that filled it.
Answer :
In the given compound Cu 2 O, the charge on Cu is +1. But the charge on copper in normal compounds is +2.
So Cu +2 will try to replace Cu +1 in atmospheric conditions.
This will lead to a generation of positive charge holes which are the cause of conductivity in p-type semiconductors.
So given compound can act as p-type semiconductors.
Answer :
Let the number of oxide ions be x.
Then, the number of octahedral voids = number of oxide ions = x.
According to question, number of ferric ions
Ratio of ferric ion: oxide ion = 2:3
So the required formula of the compound is Fe 2 O 3 .
Q 1.20(i) Classify each of the following as being either a p-type or a n-type semiconductor:
doped with
.
Answer :
We know that Ge is a group 14 element (having 4 valence electrons) and In is a group 13 element (having 3 valence electrons).
So this is a p-type semiconductor.
Q 1.20(ii) Classify each of the following as being either a or a
semiconductor:
doped with
Answer :
Si belongs to group 14 and B belongs to group 13 so it is a p-type semiconductor.
Answer :
Atomic radius = 0.144 nm
for a face-centred unit cell
the length of a side of the cell is 0.407.
Q 1.22(i) In terms of band theory, what is the difference
between a conductor and an insulator
Answer :
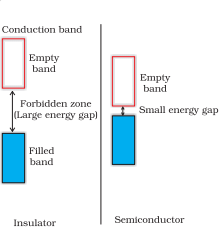
Conductor: A conductor may conduct electricity through the movement of electrons or ions. The conductivity of metals depends upon the number of valence electrons available per atom. The atomic orbitals of metal atoms form molecular orbitals which are so close in energy to each other as to form a band. If this band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily under an applied electric field and the metal shows conductivity.
Insulator: If the gap between the filled valence band and the next higher unoccupied band is large then electrons cannot jump to it and such a substance behaves as an insulator.
Q 1.22(ii) In terms of band theory, what is the difference
between a conductor and a semiconductor?
Answer :
Conductor: A conductor may conduct electricity through the movement of electrons or ions. The conductivity of metals depends upon the number of valence electrons available per atom. The atomic orbitals of metal atoms form molecular orbitals which are so close in energy to each other as to form a band. If this band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily under an applied electric field and the metal shows conductivity.
Semi-conductor: The gap between the valence band and the conduction band is small. Therefore, some electrons may jump to the conduction band and show some conductivity. The electrical conductivity of semiconductors increases with rising in temperature since more electrons can jump to the conduction band.
Q 1.23(i) Explain the following terms with suitable examples:
Schottky defect
Answer :
(i) Schottky defect
The Schottky defect is basically a vacancy defect in ionic solids. To maintain electrical neutrality, the number of missing cations and anions are equal as shown in the figure. Schottky defect decreases the density of the substance. The number of such defects in ionic solids is quite significant. For example, in NaCl, there are approximately 106 Schottky pairs per cm3 at room temperature. In 1 cm3 there are about 1022 ions. Thus, there is one Schottky defect per 1016 ions. The Schottky defect is shown by ionic substances in which the cation and anion are of almost similar sizes. For example, NaCl, KCl, CsCl and AgBr.
Q 1.23(ii) Explain the following terms with suitable examples
Frenkel defect
Answer :
(ii)Frenkel defect :
Frenkel defect is shown be ionic solids. The smaller ion (usually cation) is dislocated from its normal site to an interstitial site as shown in the figure . It creates a vacancy defect at its original site and an interstitial defect at its new site. Frenkel defect is also called a dislocation defect. Frenkel defect does not affect the density of the solid. Frenkel defect is shown by the ionic substance in which there is a large difference in the size of cations and anions, for example, ZnS, AgCl, AgBr and AgI due to the small size of cations and large size of anions, Frenkel defect can be observed in these.
Q 1.23(iii) Explain the following terms with suitable examples:
Interstitials
Answer :
Interstitial Defect: When some constituent particles (atoms or molecules) occupy an interstitial site as shown in the figure, the crystal is said to have the interstitial defect. This defect increases the density of the substance. Interstitial defects can be shown by non-ionic solids.
The figure representing the interstitial defect is as shown :

Q 1.23(iv) Explain the following terms with suitable examples
F-centres
Answer :
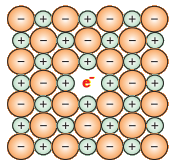
When any negative ion is absent from lattice site then result the crystal now has an excess of cations. To maintain electrical neutrality the vacant anionic site is occupied by an electron as shown in the figure.
The anionic sites occupied by unpaired electrons are called F-centres. The F- centre is responsible for most interstitial properties of the compound.
This defect can be observed in NaCl.
Answer :
For cubic close-packed structure,
we have
Given :
Answer :
For cubic close-packed structure,
we have
Given :
the volume of one unit cell
Total unit cells in 1.00 cm3
Q 1.25 If NaCl is doped with 10–3 mol % of SrCl 2 , what is the concentration of cation vacancies?
Answer :
NaCl is doped with 10–3 mol % of
Concentration in % so that take a total of 100 mol of solution.
Moles of NaCl = 100 - moles of
Moles of is very less , so we can neglect them.
Moles of NaCl =100
1 mole of NaCl is dipped with = mol of
.
So cation vacanties per mole of NaCl = mol
particles
So cation vacancies per mol of NaCl =
Hence, the concentration of cation vacancies.
Q 1.26(i) Explain the following with suitable examples:
Ferromagnetism
Answer :
(i) Ferromagnetism
Substances that are attracted very strongly by a magnetic field are called ferromagnetic substances. Example: iron, cobalt, nickel, gadolinium and CrO2. Besides strong attractions, these substances can be permanently magnetised. The metal ions of ferromagnetic substances are grouped together into small regions called domains. Thus, each domain acts as a tiny magnet. In an unmagnetised piece of a ferromagnetic substance, the domains are randomly oriented and their magnetic moments get cancelled. When the substance is placed in a magnetic field all the domains get oriented in the direction of the magnetic field as shown in the figure and a strong magnetic effect is produced. This ordering of domains persists even when the magnetic field is removed and the ferromagnetic substance becomes a permanent magnet.
The figure is as shown :
Q 1.26(ii) Explain the following with suitable examples:
Paramagnetism
Answer:
(ii) Paramagnetism :
The substances that are weakly attracted by a magnetic field are called paramagnetic substances. They are magnetised in a magnetic field in the same direction. They lose their magnetism in the absence of a magnetic field. Paramagnetism is due to the presence of one or more unpaired electrons which are attracted by the magnetic field. Example: .
Q 1.26(iii) Explain the following with suitable examples:
Ferrimagnetism
Answer :
(iii) Ferrimagnetism :
When the magnetic moments of the domains in the substance are aligned in parallel and anti-parallel directions in unequal numbers than ferrimagnetism is observed. Refer to the given figure. They are weakly attracted by a magnetic field as compared to ferromagnetic substances. Example: . These substances also lose ferrimagnetism on heating and become paramagnetic.

Q 1.26(iv) Explain the following with suitable examples:
Antiferromagnetism
Answer:
(iv) Antiferromagnetism :
Substances like MnO showing antiferromagnetism have domain structure similar to ferromagnetic substance, but their domains are oppositely oriented and cancel out each other's magnetic moment as shown in the figure.

Q 1.26(v) Explain the following with suitable examples:
12-16 and 13-15 group compounds
Answer :
(v)12-16 and 13-15 group compounds
12-16 group compounds: Compounds formed between elements of group 12 and elements of group 16 are called 12-16 group compounds.
Example: ZnS
13-15 group compounds: Compounds formed between elements of group 13 and elements of group 15 are called 13-15 group compounds.
Example: GaAs
Summary of Class 12 Chemistry Chapter 1 solid state NCERT solutions: Topics and sub-topics
- General Characteristics of Solid State
- Amorphous and Crystalline Solids
- Classification of Crystalline Solids
- Molecular Solids
- Ionic Solids
- Metallic Solids
- Covalent or Network Solids
- Crystal Lattices and Unit Cells
- Primitive and Centered Unit Cells
- Number of Atoms in a Unit Cell
- Primitive Cubic Unit Cell
- Body Centered Cubic Unit Cell
- Face Centered Cubic Unit Cell
- Close-Packed Structures
- The formula of a Compound and Number of Voids Filled
- Packing Efficiency
- Packing Efficiency in HCP and CCP Structures
- The efficiency of Packing in Body Centered Cubic Structures
- Packing Efficiency in Simple Cubic Lattice
- Calculations Involving Unit Cell Dimensions
- Imperfections in Solids
- Types of Point Defects
- Electrical Properties
- Conduction of Electricity in Metals
- Conduction of Electricity in Semiconductors
- Magnetic Properties
More about NCERT solutions for class 12 chemistry chapter 1 Solid State
NCERT solutions for class 12 chapter 1 chemistry contains questions based on topics like the correlation between the nature of interactions within the constituent particles and several properties of solids. How these properties get changed due to structural imperfections or by the presence of impurities would also be explored. It is an important chapter for the CBSE Board exam because it carries 5 marks in the chemistry examination, as well as it is important for competitive exams like JEE, NEET, BITSAT, and KVPY, etc. There are 26 questions in the exercise and 24 intext questions in this chapter. As this chapter involves conceptual knowledge rather than just learning hence it is recommended to clear your doubts to get a good hold on this chapter. You can refer to NCERT solutions for Class 12 Chemistry Chapter 1 The Solid State for clearing your doubts.
After completing NCERT solutions for class 12 chemistry chapter 1 PDF download you will be able to describe characteristics of solid-state, differentiate between amorphous solids and crystalline solids, define crystal lattice and unit cell, and also able to explain close packing of particles, describe different types of voids and close-packed structure, etc. The NCERT class 12 chemistry chapter 1 talks about only solid-state. Some of the properties of solids are -
- Solids have a definite shape and volume,
- Intermolecular force is strong
- Intermolecular distance is short
- Solids are rigid so they cannot be compressed
Topics covered in class 12 NCERT syllabus chapter Solid state:
This chapter of class 12 NCERT solid state includes concepts related to the anatomy of elements in solid state. NCERT solutions for class 12 chemistry chapter 1 discusses topics ranging from bravais lattice, unit cells and their densities, voids in a solid, magnetism etc. Class 12 NCERT solutions is a good source to practice for the board exams as direct questions are asked in the exam from this exercise. Ch 1 chemistry class 12 is helpful in physics also, especially magnetism topic. Hence it is important to practice and understand the concepts well for Chemistry Class 12 Chapter 1 to score well in the final board examination as well as competitive exams.
Crystalline and Amorphous
| Property | Crystalline solids | Amorphous solids |
| Shape | Definite geometric shape | Indefinite or irregular shape |
| Melting Point | Sharp M.P | Diffused M.P |
| Anisotropy Nature | Anisotropic | Isotropic |
NCERT Exemplar Class 12 Solutions
- NCERT Exemplar Class 12 Chemistry Solutions
- NCERT Exemplar Class 12 Mathematics Solutions
- NCERT Exemplar Class 12 Biology Solutions
- NCERT Exemplar Class 12 Physics Solutions
NCERT Solutions for Class 12 Chemistry Chapter Wise
| Chapter 1 | The Solid State |
| Chapter 2 | Solutions |
| Chapter 3 | Electrochemistry |
| Chapter 4 | Chemical Kinetics |
| Chapter 5 | Surface chemistry |
| Chapter 6 | General Principles and Processes of isolation of elements |
| Chapter 7 | The P-block elements |
| Chapter 8 | The d and f block elements |
| Chapter 9 | Coordination compounds |
| Chapter 10 | Haloalkanes and Haloarenes |
| Chapter 11 | Alcohols, Phenols, and Ethers |
| Chapter 12 | Aldehydes, Ketones and Carboxylic Acids |
| Chapter 13 | Amines |
| Chapter 14 | Biomolecules |
| Chapter 15 | Polymers |
| Chapter 16 | Chemistry in Everyday life |
Also Check NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Chemistry
- NCERT Syllabus Class 12 Chemistry
- NCERT Books Class 12
- NCERT Syllabus Class 12
Benefits of NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State
- Homework will be easy now, all you need to do is check the detailed Class 12 Chemistry Chapter 1 NCERT solutions and you are good to go.
- The revision will be a lot much easier such that you always remember the concepts and get very good marks in your class.
- The solutions which you read here in NCERT Class 12 Chemistry solutions chapter 1, will also help you in building your concepts as well as a strong base in the subject. These will also help you in various competitive exams.
- If you have a doubt or question that is not available in NCERT Solutions for Class 12 Chemistry Chapter 1 PDF download or in any of the chapters, contact us. You will get all the answers that will help you score well in your exams.
NCERT Solutions for Class 12 Subject wise
- NCERT Solutions for Class 12 Biology
- NCERT Solutions for Class 12 Maths
- NCERT Solutions for Class 12 Chemistry
- NCERT Solutions for class 12 physics
Study Well!!
Frequently Asked Question (FAQs)
- Number of octahedral voids
- Coordination Entity
- Central Atom or Ion
- Ligands
- Coordination Number
- Coordination Sphere
- Coordination Polyhedron
- Oxidation Number of Central Atom.
- Imperfections in solids
Students can find Complete solutions here: https://school.careers360.com/ncert/ncert-solutions-class-12-chemistry . they can practice these solutions to get in-depth understanding if the concepts which lead to good confidence during the exam and overall help to score well in the exam.
To prepare for Chapter 1 Solid State in NCERT Solutions for Class 12 Chemistry, it is important to have a thorough understanding of the physical properties, including the distinctions between crystalline and amorphous solids. Students should also have a clear understanding of concepts such as unit cell and crystal lattice, cubic close packing and hexagonal close packing, and octahedral and tetrahedral void. The NCERT Solutions are an essential reference material for Class 12 students preparing for CBSE exams, as they provide student-friendly explanations that aid in grasping important concepts.
Chapter 1 of NCERT Solutions for Class 12 Chemistry examines the properties of solids, which are one of the three states of matter, alongside liquids and gases. The key characteristics of solids discussed in the chapter are as follows:
- Solids have a definite mass, shape, and volume.
- Intermolecular distance in solids is short, while intermolecular force is strong.
- Solids are rigid and difficult to compress.
- The particles in solids occupy fixed positions.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
Here are some options you can explore to get admission in a good school even though admissions might be closed for many:
-
Waitlist: Many schools maintain waitlists after their initial application rounds close. If a student who secured a seat decides not to join, the school might reach out to students on the waitlist. So, even if the application deadline has passed, it might be worth inquiring with schools you're interested in if they have a waitlist and if they would consider adding you to it.
-
Schools with ongoing admissions: Some schools, due to transfers or other reasons, might still have seats available even after the main admission rush. Reach out to the schools directly to see if they have any open seats in 10th grade.
-
Consider other good schools: There might be other schools in your area that have a good reputation but weren't on your initial list. Research these schools and see if they have any seats available.
-
Focus on excelling in your current school: If you can't find a new school this year, focus on doing well in your current school. Maintain good grades and get involved in extracurricular activities. This will strengthen your application for next year if you decide to try transferring again.
Best CBSE schools in Delhi: Click Here
In India, the design and coding fields offer exciting career options that can leverage your interest in both. Here's how you can navigate this path:
Choosing Your Stream:
-
Graphic Design Focus: Consider a Bachelor's degree in Graphic Design or a design diploma. Build a strong portfolio showcasing your creative skills. Learn the basics of HTML, CSS, and JavaScript to understand web development better. Many online resources and bootcamps offer these introductory courses.
-
Coding Focus: Pursue a Computer Science degree or a coding bootcamp in India. These programs are intensive but can equip you with strong coding skills quickly. While building your coding prowess, take online courses in graphic design principles and UI/UX design.
Engineering Subjects (for a Degree):
-
Information Technology (IT): This offers a good mix of web development, networking, and database management, all valuable for web design/development roles.
-
Human-Computer Interaction (HCI): This is a specialized field that bridges the gap between design and computer science, focusing on how users interact with technology. It's a perfect choice if you're interested in both aspects.
- Passing NIOS in October 2024 will make you eligible for NIT admissions in 2025 . NIT admissions are based on your performance in entrance exams like JEE Main, which typically happen in January and April. These exams consider the previous year's Class 12th board results (or equivalent exams like NIOS).
Here's why 2025 is more likely:
- JEE Main 2024 Admissions: The application process for NITs through JEE Main 2024 is likely complete by now (May 2024). They consider your 2023 Class 12th marks (CBSE in this case).
- NIOS Results: Since NIOS results typically come out after the NIT admission process, your October 2024 NIOS marks wouldn't be available for JEE Main 2024.
Looking Ahead (2025 Admissions):
- Focus on JEE Main: Since you have a computer science background, focus on preparing for JEE Main 2025. This exam tests your knowledge in Physics, Chemistry, and Mathematics, crucial for engineering programs at NITs.
- NIOS Preparation: Utilize the time between now and October 2024 to prepare for your NIOS exams.
- Eligibility Criteria: Remember, NITs typically require a minimum of 75% marks in Class 12th (or equivalent) for general category students (65% for SC/ST). Ensure you meet this criteria in your NIOS exams.
Yes, scoring above 99.9 percentile in CAT significantly increases your chances of getting a call from IIM Bangalore, with your academic background. Here's why:
-
High CAT Score: A score exceeding 99.9 percentile is exceptional and puts you amongst the top candidates vying for admission. IIM Bangalore prioritizes CAT scores heavily in the shortlisting process.
-
Strong Academics: Your 96% in CBSE 12th and a B.Tech degree demonstrate a solid academic foundation, which IIM Bangalore also considers during shortlisting.
However, the shortlisting process is multifaceted:
- Other Factors: IIM Bangalore considers other factors beyond CAT scores, such as your work experience (if any), XAT score (if you appear for it), academic diversity, gender diversity, and performance in the interview and Written Ability Test (WAT) stages (if shortlisted).
Here's what you can do to strengthen your application:
-
Focus on WAT and PI: If you receive a shortlist, prepare extensively for the Written Ability Test (WAT) and Personal Interview (PI). These stages assess your communication, soft skills, leadership potential, and suitability for the program.
-
Work Experience (if applicable): If you have work experience, highlight your achievements and how they align with your chosen IIM Bangalore program.
Overall, with a stellar CAT score and a strong academic background, you have a very good chance of getting a call from IIM Bangalore. But remember to prepare comprehensively for the other stages of the selection process.
hello,
Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.
I hope this was helpful!
Good Luck
Popular CBSE Class 12th Questions
Colleges After 12th
Also Read
Applications for Admissions are open.

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

ALLEN Digital Scholarship Admission Test (ADSAT)
ApplyRegister FREE for ALLEN Digital Scholarship Admission Test (ADSAT)

JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

PW JEE Coaching
ApplyEnrol in PW Vidyapeeth center for JEE coaching

PW NEET Coaching
ApplyEnrol in PW Vidyapeeth center for NEET coaching

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

