NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability 2021

Q: What are the important topics in chapter Continuity and Differentiability?

Basic concepts of continuity and differentiability, derivatives of composite functions, derivatives of implicit functions, derivatives of inverse trigonometric functions, exponential and logarithmic functions, logarithmic differentiation, derivatives of functions in parametric form are the important topics in this chapter. Practice these class 12 maths ch 5 question answer to command the concepts.

Q: What are the reasons to opt for ncert continuity and differentiability solution?

The maths chapter 5 class 12 NCERT solutions created by the experts at Careers360 offer numerous advantages to students preparing for their board exams. These solutions provide comprehensive explanations of each topic, which help students achieve high scores. Additionally, the solutions are based on the latest CBSE syllabus for the 2022-23 academic year. Furthermore, these solutions also assist students in preparing for other competitive exams such as JEE Main and JEE Advanced. For ease, Students can study continuity and differentiability pdf both online and offline

Q: Which is the best book for CBSE class 12 maths ?

NCERT is the best book for CBSE class 12 maths. Most of the questions in CBSE board exam are directly asked from NCERT textbook. All you need to do is rigorous practice of all the problems given in the NCERT textbook.

Q: How many exercises are included in ncert solutions class 12 maths chapter 5?

According to the given information, there are 8 exercises in NCERT Solutions for maths chapter 5 class 12 . The following is the number of questions in each exercise: Exercise 5.1: 34 questions Exercise 5.2: 10 questions Exercise 5.3: 15 questions Exercise 5.4: 10 questions Exercise 5.5: 18 questions Exercise 5.6: 11 questions Exercise 5.7: 17 questions Exercise 5.8: 6 questions Additionally, there is a Miscellaneous Exercise with 23 questions.

Q: What is the weightage of the chapter Continuity and Differentiability for CBSE board exam ?

Generally, Continuity and differntiability has 9% weightage in the 12th board final examination. if you want to obtain meritious marks or full marks then you should have good command on concepts that can be developed by practice therefore you should practice NCERT solutions and NCERT exercise solutions.

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability

Edited By Ramraj Saini | Updated on Sep 14, 2023 07:52 PM IST | #CBSE Class 12th

NCERT Continuity And Differentiability Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 5 are provided here. These NCERT solutions are created bu expert team at careers360 considering the latest syllabus of CBSE 2023-24. Questions based on the topics like continuity, differentiability, and relations between them are covered in the NCERT solutions for class 12 maths chapter 5. In NCERT Class 12 maths book, there are 48 solved examples to understand the concepts of continuity and differentiability class 12. If you are finding difficulties in solving them, you can take help from NCERT maths chapter 5 class 12 solutions.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Continuity And Differentiability Class 12 Questions And Answers
NCERT Continuity And Differentiability Class 12 Questions And Answers PDF Free Download
Continuity And Differentiability Class 12 NCERT Solutions - Important Formulae
NCERT Continuity And Differentiability Class 12 Questions And Answers (Intext Questions and Exercise)
Topics of NCERT class 12 maths chapter 5 Continuity and Differentiability
NCERT class 12 maths ch 5 question answer - Topics
NCERT solutions for class 12 maths - Chapter wise
NCERT solutions for class 12 subject wise
NCERT Solutions class wise
NCERT Books and NCERT Syllabus
Tips to Use NCERT Solutions for Class 12 Maths Chapter 5

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability

In NCERT class 11 Maths solutions, you have already learned the differentiation of certain functions like polynomial functions and trigonometric functions. In this chapter, you will get NCERT solutions for class 12 maths chapter 5 continuity and differentiability. If you are interested in the chapter 5 class 12 maths NCERT solutions then you can check NCERT solutions for class 12 other subjects.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.

Apply Now

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

NCERT Continuity And Differentiability Class 12 Questions And Answers PDF Free Download

Download PDF

Continuity And Differentiability Class 12 NCERT Solutions - Important Formulae

>> Continuity: A function f(x) is continuous at a point x = a if:

f(a) exists (finite, definite, and real).
lim(x → a) f(x) exists.
lim(x → a) f(x) = f(a).

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

>> Discontinuity: f(x) is discontinuous in an interval if it is discontinuous at any point in that interval.

Algebra of Continuous Functions:

Sum, difference, product, and quotient of continuous functions are continuous.

Differentiation:

The derivative of f(x) at x = a, denoted as f'(a), represents the slope of the tangent line to the graph.

Chain Rule:

If f = v o u, where t = u(x), and if both dt/dx and dv/dx exist, then: df/dx = dv/dt * dt/dx.

Derivatives of Some Standard Functions:

d/dx(xⁿ) = nx^n-1
d/dx(sin x) = cos x
d/dx(cos x) = -sin x
d/dx(tan x) = sec² x
d/dx(cot x) = -csc² x
d/dx(sec x) = sec x * tan x
d/dx(csc x) = -csc x * cot x
d/dx(a^x) = a^x * ln(a)
d/dx(e^x) = e^x
d/dx(ln x) = 1/x

SAT® | CollegeBoard

Apply

TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Mean Value Theorem:

Mean Value Theorem states that if f(x) is continuous on [a, b] and differentiable on (a, b), then there exists some c in (a, b) such that: f'(c) = (f(b) - f(a)) / (b - a).

Rolle's Theorem:

Rolle's Theorem states that if f(x) is continuous on [a, b], differentiable on (a, b), and f(a) = f(b), then there exists some c in (a, b) such that f'(c) = 0.

Lagrange's Mean Value Theorem:

Lagrange's Mean Value Theorem states that if f(x) is continuous on [a, b] and differentiable on (a, b), then there exists some c in (a, b) such that:

f'(c) = (f(b) - f(a)) / (b - a).

Free download Continuity And Differentiability Class 12 NCERT Solutions for CBSE Exam.

NCERT Continuity And Differentiability Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT Continuity And Differentiability Class 12 Solutions : Excercise: 5.1

Question:1 . Prove that the function $f ( x) = 5 x -3$ is continuous at $x = 0, at\: \: x = - 3$ and at $x = 5$

Answer:

Given function is
$f ( x) = 5 x -3$
$f(0) = 5(0)-3 = -3$
$\lim_{x\rightarrow 0} f(x) = 5(0)-3 = -3$
$\lim_{x\rightarrow 0} f(x) =f(0)$
Hence, function is continous at x = 0

$f(-3)= 5(-3)-3=-15-3=-18\\\Rightarrow \lim_{x\rightarrow -3} f(x) = 5(-3)-3 = -15-3=-18\\\Rightarrow \lim_{x\rightarrow -3} f(x) = f(-3)$
Hence, function is continous at x = -3

$f(5)= 5(5)-3=25-3=22\\\Rightarrow \lim_{x\rightarrow 5} f(x) = 5(5)-3 = 25-3=-22\\ \Rightarrow \lim_{x\rightarrow 5} f(x) = f(5)$
Hence, function is continuous at x = 5

Question:2 . Examine the continuity of the function $f (x) = 2x ^2 - 1 \: \: at\: \: x = 3.$

Answer:

Given function is
$f(x) = 2x^2-1$
at x = 3
$f(3) = 2(3)^2-1 = 2\times 9 - 1=18-1=17\\ \lim_{x\rightarrow 3}f(x) = 2(3)^2-1=2\times 9-1=18-1=17$
$\lim_{x\rightarrow 3}f(x) = f(3)$
Hence, function is continous at x = 3

Question:3 Examine the following functions for continuity.
$(a) f (x) = x - 5$

Answer:

Given function is
$f(x) = x-5$
Our function is defined for every real number say k
and value at x = k , $f(k) = k-5$
and also,
$\lim_{x\rightarrow k} f(x) = k -5\\ \lim_{x\rightarrow k} f(x) = f(k)$
Hence, the function $f(x) = x-5$ is continuous at every real number

Question:3 b) Examine the following functions for continuity.

$f (x) = \frac{1}{x-5} , x \neq 5$

Answer:

Given function is
$f(x ) = \frac{1}{x-5}$
For every real number k , $k \neq 5$
We get,
$f(k) = \frac{1}{k-5}\\ \lim_{x\rightarrow k}f(x ) = \frac{1}{k-5}\\ \lim_{x\rightarrow k}f(x ) = f(k)$
Hence, function $f(x ) = \frac{1}{x-5}$ continuous for every real value of x, $x \neq 5$

Question:3 c) Examine the following functions for continuity.

$f (x) = \frac{x ^2-25}{x+5}, x \neq -5$

Answer:

Given function is
$f(x ) = \frac{x^2-25}{x+5}$
For every real number k , $k \neq -5$
We gwt,
$f(k) = \frac{k^2-5^2}{k+5}= \frac{(k +5)(k-5)}{k+5} = k-5\\ \lim_{x\rightarrow k}f(x ) = \frac{k^2-5^2}{k+5}= \frac{(k +5)(k-5)}{k+5} = k-5\\ \lim_{x\rightarrow k}f(x ) = f(k)$
Hence, function $f(x ) = \frac{x^2-25}{x+5}$ continuous for every real value of x , $x \neq -5$

Question:3 d) Examine the following functions for continuity. $f (x) = | x - 5|$

Answer:

Given function is
$f (x) = | x - 5|$
for x > 5 , f(x) = x - 5
for x < 5 , f(x) = 5 - x
SO, different cases are their
case(i) x > 5
for every real number k > 5 , f(x) = x - 5 is defined
$f(k) = k - 5\\ \lim_{x\rightarrow k }f(x) = k -5\\ \lim_{x\rightarrow k }f(x) = f(k)$
Hence, function f(x) = x - 5 is continous for x > 5

case (ii) x < 5
for every real number k < 5 , f(x) = 5 - x is defined
$f(k) = 5-k\\ \lim_{x\rightarrow k }f(x) = 5 -k\\ \lim_{x\rightarrow k }f(x) = f(k)$
Hence, function f(x) = 5 - x is continous for x < 5

case(iii) x = 5
for x = 5 , f(x) = x - 5 is defined
$f(5) = 5 - 5=0\\ \lim_{x\rightarrow 5 }f(x) = 5 -5=0\\ \lim_{x\rightarrow 5 }f(x) = f(5)$
Hence, function f(x) = x - 5 is continous for x = 5

Hence, the function $f (x) = | x - 5|$ is continuous for each and every real number

Question:4 . Prove that the function $f (x) = x^n$ is continuous at x = n, where n is a positive integer

Answer:

GIven function is
$f (x) = x^n$
the function $f (x) = x^n$ is defined for all positive integer, n
$f(n) = n^n\\ \lim_{x\rightarrow n}f(x) = n^n\\ \lim_{x\rightarrow n}f(x) = f(n)$
Hence, the function $f (x) = x^n$ is continuous at x = n, where n is a positive integer

Question:5. Is the function f defined by
$f (x) = \left\{\begin{matrix} x , & if x \leq 1 \\ 5 & if x \geq 1 \end{matrix}\right.$
continuous at x = 0? At x = 1? At x = 2?

Answer:

Given function is
$f (x) = \left\{\begin{matrix} x , & if x \leq 1 \\ 5 & if x \geq 1 \end{matrix}\right.$
function is defined at x = 0 and its value is 0
$f(0) = 0\\ \lim_{x\rightarrow 0}f(x) = f(x) = 0\\ \lim_{x\rightarrow 0}f(x) = f(0)$
Hence , given function is continous at x = 0

given function is defined for x = 1
Now, for x = 1 Right-hand limit and left-hand limit are not equal
$f(1) = 1\\ \lim_{x\rightarrow 1^-}f(x) = f(x) = 1\\ \lim_{x\rightarrow 1^+}f(x) =f(5) = 5$
R.H.L $\neq$ L.H.L.
Therefore, given function is not continous at x =1
Given function is defined for x = 2 and its value at x = 2 is 5
$f(2) = 2\\ \lim_{x\rightarrow 2}f(x) = f(5) = 5\\\lim_{x\rightarrow 2}f(x) = f(2)$
Hence, given function is continous at x = 2

Question:6. Find all points of discontinuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} 2x+3 & if x \leq 2 \\ 2x-3 & if x \geq 2 \end{matrix}\right.$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} 2x+3 & if x \leq 2 \\ 2x-3 & if x \geq 2 \end{matrix}\right.$
given function is defined for every real number k
There are different cases for the given function
case(i) k > 2
$f(k) = 2k-3\\ \lim_{x\rightarrow k}f(x) = 2k-3\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k > 2

case(ii) k < 2
$f(k) = 2k +3\\ \lim_{x\rightarrow k}f(x) = 2k+3\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k < 2

case(iii) x = 2

$\lim_{x\rightarrow 2^-}f(x) = 2x+3 = 2\times 2 + 3 = 4 + 3 = 7\\ \lim_{x\rightarrow 2^+}f(x) = 2x-3 = 2\times 2-3 = 4-3 = 1$
Right hand limit at x= 2 $\neq$ Left hand limit at x = 2
Therefore, x = 2 is the point of discontinuity

Question:7. Find all points of discontinuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} |x|+3 & if \: \: x \leq -3 & \\ -2x & if \: \: -3 <x< 3 & \\ 6x +2 & if \: \: x \geq 3 & \end{matrix}\right.$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} |x|+3 & if \: \: x \leq -3 & \\ -2x & if \: \: -3 <x< 3 & \\ 6x +2 & if \: \: x \geq 3 & \end{matrix}\right.$
GIven function is defined for every real number k
Different cases are their
case (i) k < -3
$f(k) = -k + 3\\ \lim_{x\rightarrow k}f(x) = -k + 3\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for every value of k < -3

case(ii) k = -3
$f(-3) = -(-3) + 3 = 6\\ \lim_{x\rightarrow -3^-}f(x) = -k + 3=-(-3)+3 = 6\\ \lim_{x\rightarrow -3^+}f(x) = -2x = -2(-3) = 6\\ R.H.L. = L.H.L. = f(-3)$
Hence, given function is continous for x = -3

case(iii) -3 < k < 3
$f(k) = -2k \\ \lim_{x\rightarrow k}f(x) = -2k\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, for every value of k in -3 < k < 3 given function is continous

case(iv) k = 3
$f(3) = 6x+2 = 6\times3+2 =18+2=20\\ \lim_{x\rightarrow 3^-}f(x) = -2x = -2(3) = -6\\ \lim_{x\rightarrow 3^+}f(x) = 6x+2 = 6\times3+2 = 20\\ R.H.L. = f(3) \neq L.H.L.$
Hence . x = 3 is the point of discontinuity

case(v) k > 3
$f(k) = 6k+2 \\ \lim_{x\rightarrow k}f(x) = 6k+2 \\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each and every value of k > 3

Question:8. Find all points of discontinuity of f, where f is defined by

$f (x )= \left\{\begin{matrix} \frac{|x|}{x} & if \: \: x \neq 0 \\ 0 & if \: \: x = 0 \end{matrix}\right.$

Answer:

Given function is
$f (x ) \left\{\begin{matrix} \frac{|x|}{x} & if \: \: x \neq 0 \\ 0 & if \: \: x = 0 \end{matrix}\right.$
if x > 0 , $f(x)=\frac{x}{x} = 1$
if x < 0 , $f(x)=\frac{-(x)}{x} = -1$
given function is defined for every real number k
Now,
case(i) k < 0
$f(k) = -1\\ \lim_{x\rightarrow k }f(x) = -1\\ \lim_{x\rightarrow k }f(x) = f(k)$
Hence, given function is continuous for every value of k < 0
case(ii) k > 0
$f(k) = 1\\ \lim_{x\rightarrow k }f(x) = 1\\ \lim_{x\rightarrow k }f(x) = f(k)$
Hence, given function is continuous for every value of k > 0
case(iii) x = 0
$f(0) = 0\\ \lim_{x\rightarrow 0^- }f(x) = -1\\ \lim_{x\rightarrow 0^+}f(x) = 1\\ f(0) \neq R.H.L. \neq L.H.L.$
Hence, 0 is the only point of discontinuity

Question:9. Find all points of discontinuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} \frac{x }{|x|} & if \: \: x < 0\\ -1 & if x \geq 0 \end{matrix}\right.$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} \frac{x }{|x|} & if \: \: x < 0\\ -1 & if x \geq 0 \end{matrix}\right.$
if x < 0 , $f (x) =\frac{x }{|x|} = \frac{x}{-(x)} = -1$
Now, for any value of x, the value of our function is -1
Therefore, the given function is continuous for each and every value of x
Hence, no point of discontinuity

Question:10. Find all points of discontinuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} x+1 & if \: \: x \geq 1 \\ x^2 +1 & if x \: \: <1 \end{matrix}\right.$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} x+1 & if \: \: x \geq 1 \\ x^2 +1 & if x \: \: <1 \end{matrix}\right.$
given function is defined for every real number k
There are different cases for the given function
case(i) k > 1
$f(k) = k+1\\ \lim_{x\rightarrow k}f(x) = k+1\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k > 1

case(ii) k < 1
$f(k) = k^2 ++1\\ \lim_{x\rightarrow k}f(x) = k^2+1\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k < 1

case(iii) x = 1

$\lim_{x\rightarrow 1^-}f(x) = x^2+1 = 1^2 + 1 = 1 + 1 = 2\\ \lim_{x\rightarrow 1^+}f(x) = x+1 = 1+1 = 2\\ f(1) = 1^2+1 = 2 \\ R.H.L. = L.H.L. = f(1)$

Hence, at x = 2 given function is continuous
Therefore, no point of discontinuity

Question:11. Find all points of discontinuity of f, where f is defined by

$f ( x) = \left\{\begin{matrix} x^3 -3 & if \: \: x \leq 2\\ x ^2 +1 & if \: \: x > 2 \end{matrix}\right.$

Answer:

Given function is
$f ( x) = \left\{\begin{matrix} x^3 -3 & if \: \: x \leq 2\\ x ^2 +1 & if \: \: x > 2 \end{matrix}\right.$
given function is defined for every real number k
There are different cases for the given function
case(i) k > 2
$f(k) = k^2+1\\ \lim_{x\rightarrow k}f(x) = k^2+1\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k > 2

case(ii) k < 2
$f(k) = k^3 -3\\ \lim_{x\rightarrow k}f(x) = k^3-3\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k < 2

case(iii) x = 2

$\lim_{x\rightarrow 2^-}f(x) = x^3-3 = 2^3- 3 = 8- 3 = 5\\ \lim_{x\rightarrow 2^+}f(x) = x^2+1= 2^2+1 = 4+1 = 5\\ f(2) = 2^3-3 = 8 - 3 = 5\\ f(2)=R.H.L.=L.H.L.$
Hence, given function is continuous at x = 2
There, no point of discontinuity

Question:12. Find all points of discontinuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} x ^{10} -1 & if x \leq 1 \\ x ^2 & x > 1 \end{matrix}\right.$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} x ^{10} -1 & if x \leq 1 \\ x ^2 & x > 1 \end{matrix}\right.$
given function is defined for every real number k
There are different cases for the given function
case(i) k > 1
$f(k) = k^2\\ \lim_{x\rightarrow k}f(x) = k^2\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k > 1

case(ii) k < 1
$f(k) = k^{10} -1\\ \lim_{x\rightarrow k}f(x) = k^{10}-1\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k < 1

case(iii) x = 1

$\lim_{x\rightarrow 1^-}f(x) = x^{10}-1 = 1^{10} - 1 = 1 - 1 = 0\\ \lim_{x\rightarrow 1^+}f(x) = x^2 = 1^2 = 1\\ f(1) = x^{10}-1 = 0\ f(1) = L.H.L. \neq R.H.L.$

Hence, x = 1 is the point of discontinuity

Question:13. Is the function defined by

$f (x) = \left\{\begin{matrix} x+5 & if x \leq 1\\ x-5 & if x > 1 \end{matrix}\right.$

a continuous function?

Answer:

Given function is
$f (x) = \left\{\begin{matrix} x+5 & if x \leq 1\\ x-5 & if x > 1 \end{matrix}\right.$
given function is defined for every real number k
There are different cases for the given function
case(i) k > 1
$f(k) = k-5\\ \lim_{x\rightarrow k}f(x) = k-5\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k > 1

case(ii) k < 1
$f(k) = k+5\\ \lim_{x\rightarrow k}f(x) = k+5\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for each value of k < 1

case(iii) x = 1

$\lim_{x\rightarrow 1^-}f(x) = x+5 = 1 + 5 = 1 + 5 = 6\\ \lim_{x\rightarrow 1^+}f(x) = x-5 = 1-5 = -4\\ f(1) = x+5 =1+5= 6 \\ L.H.L. = f(1) \neq R.H.S.$

Hence, x = 1 is the point of discontinuity

Question:14. Discuss the continuity of the function f, where f is defined by

$f (x)\left\{\begin{matrix} 3 & if 0 \leq x \leq 1 \\ 4& if 1 < x < 3 \\ 5& if 3 \leq x \leq 10 \end{matrix}\right.$

Answer:

Given function is
$f (x)\left\{\begin{matrix} 3 & if 0 \leq x \leq 1 \\ 4& if 1 < x < 3 \\ 5& if 3 \leq x \leq 10 \end{matrix}\right.$
GIven function is defined for every real number k
Different cases are their
case (i) k < 1
$f(k) = 3\\ \lim_{x\rightarrow k}f(x) = 3\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continous for every value of k < 1

case(ii) k = 1
$f(1) = 3 \\ \lim_{x\rightarrow 1^-}f(x) = 3\\ \lim_{x\rightarrow 1^+}f(x) = 4\\ R.H.L. \neq L.H.L. = f(1)$
Hence, given function is discontinous at x = 1
Therefore, x = 1 is he point od discontinuity

case(iii) 1 < k < 3
$f(k) = 4 \\ \lim_{x\rightarrow k}f(x) = 4\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, for every value of k in 1 < k < 3 given function is continous

case(iv) k = 3
$f(3) =5\\ \lim_{x\rightarrow 3^-}f(x) = 4\\ \lim_{x\rightarrow 3^+}f(x) =5\\ R.H.L. = f(3) \neq L.H.L.$
Hence. x = 3 is the point of discontinuity

case(v) k > 3
$f(k) = 5 \\ \lim_{x\rightarrow k}f(x) = 5 \\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continous for each and every value of k > 3
case(vi) when k < 3

$f(k) = 4 \\ \lim_{x\rightarrow k}f(x) = 4\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, for every value of k in k < 3 given function is continous

Question:15 Discuss the continuity of the function f, where f is defined by $f(x)\left\{\begin{matrix} 2x & if &x<0 \\ 0& if &0\leq x\leq 1 \\ 4x&if & x>1 \end{matrix}\right.$

Answer:

Given function is
$gif$
Given function is satisfies for the all real values of x
case (i) k < 0
$gif$
$gif$
Hence, function is continuous for all values of x < 0

case (ii) x = 0
$gif$
L.H.L at x= 0
$gif$
R.H.L. at x = 0
$gif$
L.H.L. = R.H.L. = f(0)
Hence, function is continuous at x = 0

case (iii) k > 0
$gif$
$gif$
Hence , function is continuous for all values of x > 0

case (iv) k < 1
$gif$
$gif$
Hence , function is continuous for all values of x < 1

case (v) k > 1
$gif$
$gif$
Hence , function is continuous for all values of x > 1

case (vi) x = 1
$gif$
$gif$
$gif$
Hence, function is not continuous at x = 1

Question:16. Discuss the continuity of the function f, where f is defined by

$f ( x ) = \left\{\begin{matrix} -2 & if x \leq -1 \\ 2x & if -1< x \leq 1 \\ 2 & if x > 1 \end{matrix}\right.$

Answer:

Given function is
$f ( x ) = \left\{\begin{matrix} -2 & if x \leq -1 \\ 2x & if -1< x \leq 1 \\ 2 & if x > 1 \end{matrix}\right.$
GIven function is defined for every real number k
Different cases are their
case (i) k < -1
$f(k) = -2\\ \lim_{x\rightarrow k}f(x) = -2\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continuous for every value of k < -1

case(ii) k = -1
$f(-1) = -2 \\ \lim_{x\rightarrow -1^-}f(x) = -2\\ \lim_{x\rightarrow -1^+}f(x) = 2x = 2(-1) = -2\\ R.H.L. =L.H.L. = f(-1)$
Hence, given function is continous at x = -1

case(iii) k > -1
$f(k) = 2k \\ \lim_{x\rightarrow k}f(x) = 2k\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continous for all values of x > -1

case(vi) -1 < k < 1
$f(k) = 2k \\ \lim_{x\rightarrow k}f(x) = 2k\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, for every value of k in -1 < k < 1 given function is continous

case(v) k = 1
$f(1) =2x = 2(1)=2\\ \lim_{x\rightarrow 1^-}f(x) = 2x=2(1)=2\\ \lim_{x\rightarrow 1^+}f(x) =2\\ R.H.L. = f(1) = L.H.L.$
Hence.at x =1 function is continous

case(vi) k > 1
$f(k) = 2 \\ \lim_{x\rightarrow k}f(x) = 2 \\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, given function is continous for each and every value of k > 1
case(vii) when k < 1

$f(k) = 2k \\ \lim_{x\rightarrow k}f(x) = 2k\\ \lim_{x\rightarrow k}f(x) = f(k)$
Hence, for every value of k in k < 1 given function is continuous

Therefore, continuous at all points

Question:17. Find the relationship between a and b so that the function f defined by
$f (x) = \left\{\begin{matrix} ax +1 , &if x < 3 \\ bx +3 & if x > 3 \end{matrix}\right.$
is continuous at x = 3.

Answer:

Given function is
$f (x) = \left\{\begin{matrix} ax +1 , &if x < 3 \\ bx +3 & if x > 3 \end{matrix}\right.$
For the function to be continuous at x = 3 , R.H.L. must be equal to L.H.L.
$\lim_{x\rightarrow 3^-}f(x)= ax + 1 = 3a+1\\ \lim_{x\rightarrow 3^+}f(x) = bx+3=3b+3$
For the function to be continuous
$\lim_{x\rightarrow 3^-}f(x) = \lim_{x\rightarrow 3^+}f(x) \\ 3a + 1= 3b+3\\ 3(a-b)=2\\ a-b = \frac{2}{3}\\ a = b+\frac{2}{3}$

Question:18. For what value of l is the function defined by
$f (x) = \left\{\begin{matrix} \lambda (x^2 -2x) & if x \leq 0 \\ 4x+1 & if x > 0 \end{matrix}\right.$
continuous at x = 0? What about continuity at x = 1?

Answer:

Given function is
$f (x) = \left\{\begin{matrix} \lambda (x^2 -2x) & if x \leq 0 \\ 4x+1 & if x > 0 \end{matrix}\right.$
For the function to be continuous at x = 0 , R.H.L. must be equal to L.H.L.
$\lim_{x\rightarrow 0^-}f(x) = \lambda (x^2-2x) = 0\\ \lim_{x\rightarrow 0^+}f(x) = 4x+1=1$
For the function to be continuous
$\lim_{x\rightarrow 0^-}f(x) = \lim_{x\rightarrow 0^+}f(x) \\ 0\neq 1$
Hence, for no value of function is continuous at x = 0

For x = 1
$f(1)=4x+1=4(1)+1=5\\ \lim_{x\rightarrow 1}f(x) =4+1=5 \\\ \lim_{x\rightarrow 1}f(x) = f(x)$
Hence, given function is continuous at x =1

Question:19. Show that the function defined by $g (x) = x- [x]$ is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.

Answer:

Given function is
$g (x) = x- [x]$
Given is defined for all real numbers k
$\lim_{x\rightarrow k^-}f(x) = k - (k-1) = k-k+1 =1\\ \lim_{x\rightarrow k^+}f(x) = k - k = 0\\ \lim_{x\rightarrow k^-}f(x) \neq \lim_{x\rightarrow k^+}f(x)$
Hence, by this, we can say that the function defined by $g (x) = x- [x]$ is discontinuous at all integral points

Question:20. Is the function defined by $f (x) = x^2 - sin x + 5$ continuous at x = $\pi$ ?

Answer:

Given function is
$f (x) = x^2 - sin x + 5$
Clearly, Given function is defined at x = $\pi$
$f(\pi) = \pi^2-\sin \pi+5 =\pi^2-0+5 = \pi^2+5\\ \lim_{x\rightarrow \pi}f(x) = \pi^2-\sin \pi+5 =\pi^2-0+5 = \pi^2+5\\ \lim_{x\rightarrow \pi}f(x) = f(\pi)$
Hence, the function defined by $f (x) = x^2 - sin x + 5$ continuous at x = $\pi$

Question:21. Discuss the continuity of the following functions:
a) $f (x) = \sin x + \cos x$

Answer:

Given function is
$f (x) = \sin x + \cos x$
Given function is defined for all real number
We, know that if two function g(x) and h(x) are continuous then g(x)+h(x) , g(x)-h(x) , g(x).h(x) allare continuous
Lets take g(x) = sin x and h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$g(c) = \sin c\\ \lim_{x\rightarrow c}g(x) = \lim_{x\rightarrow c}\sin x = \lim_{h\rightarrow 0}\sin (c+h)\\ We \ know \ that\\ \sin(a+b) = \sin a \cos b + \cos a\sin b\\ \lim_{h\rightarrow 0}\sin (c+h) = \lim_{h\rightarrow 0}(\sin c\cos h + \cos c \sin h) = \lim_{h\rightarrow 0}\sin c\cos h + \lim_{h\rightarrow 0}\cos c \sin h$
$=\sin c\cos 0 + \cos c \sin 0 = \sin c$
$\lim_{x\rightarrow c}g(x) = g(c)$
Hence, function $g(x) = \sin x$ is a continuous function
Now,
h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \cos c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\cos x = \lim_{h\rightarrow 0}\cos (c+h)\\ We \ know \ that\\ \cos(a+b) = \cos a \cos b + \sin a\sin b\\ \lim_{h\rightarrow 0}\cos (c+h) = \lim_{h\rightarrow 0}(\cos c\cos h + \sin c \sin h) = \lim_{h\rightarrow 0}\cos c\cos h + \lim_{h\rightarrow 0}\sin c \sin h$
$=\cos c\cos 0 + \sin c \sin 0 = \cos c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, function $h(x) = \cos x$ is a continuous function
We proved independently that sin x and cos x is continous function
So, we can say that
f(x) = g(x) + h(x) = sin x + cos x is also a continuous function

Question:21. b) Discuss the continuity of the following functions:
$f (x) = \sin x - \cos x$

Answer:

Given function is
$f (x) = \sin x - \cos x$
Given function is defined for all real number
We, know that if two function g(x) and h(x) are continuous then g(x)+h(x) , g(x)-h(x) , g(x).h(x) allare continuous
Lets take g(x) = sin x and h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$g(c) = \sin c\\ \lim_{x\rightarrow c}g(x) = \lim_{x\rightarrow c}\sin x = \lim_{h\rightarrow 0}\sin (c+h)\\ We \ know \ that\\ \sin(a+b) = \sin a \cos b + \cos a\sin b\\ \lim_{h\rightarrow 0}\sin (c+h) = \lim_{h\rightarrow 0}(\sin c\cos h + \cos c \sin h) = \lim_{h\rightarrow 0}\sin c\cos h + \lim_{h\rightarrow 0}\cos c \sin h$
$=\sin c\cos 0 + \cos c \sin 0 = \sin c$
$\lim_{x\rightarrow c}g(x) = g(c)$
Hence, function $g(x) = \sin x$ is a continuous function
Now,
h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \cos c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\cos x = \lim_{h\rightarrow 0}\cos (c+h)\\ We \ know \ that\\ \cos(a+b) = \cos a \cos b + \sin a\sin b\\ \lim_{h\rightarrow 0}\cos (c+h) = \lim_{h\rightarrow 0}(\cos c\cos h + \sin c \sin h) = \lim_{h\rightarrow 0}\cos c\cos h + \lim_{h\rightarrow 0}\sin c \sin h$
$=\cos c\cos 0 + \sin c \sin 0 = \cos c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, function $h(x) = \cos x$ is a continuous function
We proved independently that sin x and cos x is continous function
So, we can say that
f(x) = g(x) - h(x) = sin x - cos x is also a continuous function

Question:21 c) Discuss the continuity of the following functions:
$f (x) = \sin x \cdot \cos x$

Answer:

Given function is
$f (x) = \sin x . \cos x$
Given function is defined for all real number
We, know that if two function g(x) and h(x) are continuous then g(x)+h(x) , g(x)-h(x) , g(x).h(x) allare continuous
Lets take g(x) = sin x and h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$g(c) = \sin c\\ \lim_{x\rightarrow c}g(x) = \lim_{x\rightarrow c}\sin x = \lim_{h\rightarrow 0}\sin (c+h)\\ We \ know \ that\\ \sin(a+b) = \sin a \cos b + \cos a\sin b\\ \lim_{h\rightarrow 0}\sin (c+h) = \lim_{h\rightarrow 0}(\sin c\cos h + \cos c \sin h) = \lim_{h\rightarrow 0}\sin c\cos h + \lim_{h\rightarrow 0}\cos c \sin h$
$=\sin c\cos 0 + \cos c \sin 0 = \sin c$
$\lim_{x\rightarrow c}g(x) = g(c)$
Hence, function $g(x) = \sin x$ is a continuous function
Now,
h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \cos c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\cos x = \lim_{h\rightarrow 0}\cos (c+h)\\ We \ know \ that\\ \cos(a+b) = \cos a \cos b + \sin a\sin b\\ \lim_{h\rightarrow 0}\cos (c+h) = \lim_{h\rightarrow 0}(\cos c\cos h + \sin c \sin h) = \lim_{h\rightarrow 0}\cos c\cos h + \lim_{h\rightarrow 0}\sin c \sin h$
$=\cos c\cos 0 + \sin c \sin 0 = \cos c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, function $h(x) = \cos x$ is a continuous function
We proved independently that sin x and cos x is continous function
So, we can say that
f(x) = g(x).h(x) = sin x .cos x is also a continuous function

Question:22. Discuss the continuity of the cosine, cosecant, secant and cotangent functions.

Answer:

We, know that if two function g(x) and h(x) are continuous then
$\frac{g(x)}{h(x)} , h(x) \neq0\ is \ continuous\\ \frac{1}{h(x)} , h(x) \neq 0\ is \ continuous\\ \frac{1}{g(x)} , g(x) \neq0\ is \ continuous\\$
Lets take g(x) = sin x and h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$g(c) = \sin c\\ \lim_{x\rightarrow c}g(x) = \lim_{x\rightarrow c}\sin x = \lim_{h\rightarrow 0}\sin (c+h)\\ We \ know \ that\\ \sin(a+b) = \sin a \cos b + \cos a\sin b\\ \lim_{h\rightarrow 0}\sin (c+h) = \lim_{h\rightarrow 0}(\sin c\cos h + \cos c \sin h) = \lim_{h\rightarrow 0}\sin c\cos h + \lim_{h\rightarrow 0}\cos c \sin h$
$=\sin c\cos 0 + \cos c \sin 0 = \sin c$
$\lim_{x\rightarrow c}g(x) = g(c)$
Hence, function $g(x) = \sin x$ is a continuous function
Now,
h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \cos c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\cos x = \lim_{h\rightarrow 0}\cos (c+h)\\ We \ know \ that\\ \cos(a+b) = \cos a \cos b + \sin a\sin b\\ \lim_{h\rightarrow 0}\cos (c+h) = \lim_{h\rightarrow 0}(\cos c\cos h + \sin c \sin h) = \lim_{h\rightarrow 0}\cos c\cos h + \lim_{h\rightarrow 0}\sin c \sin h$
$=\cos c\cos 0 + \sin c \sin 0 = \cos c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, the function $h(x) = \cos x$ is a continuous function
We proved independently that sin x and cos x is a continous function
So, we can say that
cosec x = $\frac{1}{\sin x} = \frac{1}{g(x)}$ is also continuous except at $x=n\pi$
sec x = $\frac{1}{\cos x} = \frac{1}{h(x)}$ is also continuous except at $x=\frac{(2n+1) \pi}{2}$
cot x = $\frac{\cos x}{\sin x} = \frac{h(x)}{g(x)}$ is also continuous except at $x=n\pi$

Question:23. Find all points of discontinuity of f, where

$f (x ) = \left\{\begin{matrix} \frac{\sin x }{x} & if x < 0 \\ x+1 & if x > 0 \end{matrix}\right.$

Answer:

Given function is
$f (x ) = \left\{\begin{matrix} \frac{\sin x }{x} & if x < 0 \\ x+1 & if x > 0 \end{matrix}\right.$
$\lim_{x\rightarrow 0^-}f(x) = \lim_{x\rightarrow 0}\frac{\sin x}{x} = 1\\ \lim_{x\rightarrow 0^+}f(x) = x + 1 = 1\\ \lim_{x\rightarrow 0^-}f(x) = \lim_{x\rightarrow 0^+}f(x)$
Hence, the function is continuous
Therefore, no point of discontinuity

Question:24. Determine if f defined by
$f (x) = \left\{\begin{matrix} x^2 \sin 1/x & if x \neq 0 \\ 0 & if x = 0 \end{matrix}\right.$
is a continuous function?

Answer:

Given function is
$f (x) = \left\{\begin{matrix} x^2 \sin 1/x & if x \neq 0 \\ 0 & if x = 0 \end{matrix}\right.$
Given function is defined for all real numbers k
when x = 0
$f(0) = 0\\ \lim_{x\rightarrow 0}f(x)=\lim_{x\rightarrow 0}\left ( x^2\sin\frac{1}{x} \right )=\lim_{x\rightarrow 0}\left ( \frac{x.\sin\frac{1}{x}}{\frac{1}{x}} \right ) = 0(1)=0 \ \ \ \ \ \ (\because\lim_{x\rightarrow 0}\frac{\sin x}{x} = 1)$
$\lim_{x\rightarrow 0}f(x) = f(0)$
Hence, function is continuous at x = 0
when $x \neq 0$
$f(k) = k^2\sin \frac{1}{k}\\ \lim_{x\rightarrow k}f(x)=\lim_{x\rightarrow k}\left ( x^2\sin\frac{1}{x} \right )=k^2\sin \frac{1}{k}\\ \lim_{x\rightarrow k} = f(k)$
Hence, the given function is continuous for all points

Question:25 . Examine the continuity of f, where f is defined by

$f (x) = \left\{\begin{matrix} \sin x - \cos x & if x \neq 0 \\ -1 & if x = 0 \end{matrix}\right.$

Answer:

Question:26. Find the values of k so that the function f is continuous at the indicated point in Exercises

$f (x) = \left\{\begin{matrix} \frac{k \cos x }{\pi - 2x } & if x \neq \pi/2 \\ 3 & if x = \pi/2 \end{matrix}\right. \: \: \: at \: \: x = \pi /2$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} \frac{k \cos x }{\pi - 2x } & if x \neq \pi/2 \\ 3 & if x = \pi/2 \end{matrix}\right.$
When $x = \frac{\pi}{2}$
$f(\frac{\pi}{2}) = 3\\let\ x=\pi +h\\ \lim_{x\rightarrow \frac{\pi}{2}}f(x)= \lim_{h\rightarrow 0}\frac{k\cos\left ( \frac{\pi}{2}+h \right )}{\pi-2\left ( \frac{\pi}{2}+h \right )} = k. \lim_{h\rightarrow 0}\frac{-\sin h}{-2h} = \frac{k}{2}\\$
For the function to be continuous
$\lim_{x\rightarrow \frac{\pi}{2}}f(x)= f(\frac{\pi}{2})\\ \frac{k}{2} = 3\\ k = 6$
Therefore, the values of k so that the function f is continuous is 6

Question:27 . Find the values of k so that the function f is continuous at the indicated point in Exercises

$f (x) = \left\{\begin{matrix} kx^2 &if x \leq 2 \\ 3 & if x > 2 \end{matrix}\right. \: \: at \: \: x = 2$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} kx^2 &if x \leq 2 \\ 3 & if x > 2 \end{matrix}\right.$
When x = 2
For the function to be continuous
f(2) = R.H.L. = LH.L.
$f(2) = 4k\\ \lim_{x\rightarrow 2^-}f(x)= 4k\\ \lim_{x\rightarrow 2^+}f(x) = 3\\ f(2) = \lim_{x\rightarrow 2^-}f(x) = \lim_{x\rightarrow 2^+}f(x)\\ 4k = 3\\ k = \frac{3}{4}$
Hence, the values of k so that the function f is continuous at x= 2 is $\frac{3}{4}$

Question:28 . Find the values of k so that the function f is continuous at the indicated point in Exercises

$f (x) = \left\{\begin{matrix} kx + 1 & if x \leq \pi \\ \cos x & if x > \pi \end{matrix}\right. \: \: at \: \: x = \pi$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} kx + 1 & if x \leq \pi \\ \cos x & if x > \pi \end{matrix}\right.$
When x = $\pi$
For the function to be continuous
f( $\pi$ ) = R.H.L. = LH.L.
$f(\pi) = k\pi+1\\ \lim_{x\rightarrow \pi^-}f(x)= k\pi+1\\ \lim_{x\rightarrow \pi^+}f(x) = \cos \pi = -1\\ f(\pi) = \lim_{x\rightarrow \pi^-}f(x) = \lim_{x\rightarrow \pi^+}f(x)\\ k\pi+1 = -1\\ k = \frac{-2}{\pi}$
Hence, the values of k so that the function f is continuous at x= $\pi$ is $\frac{-2}{\pi}$

Question:29 Find the values of k so that the function f is continuous at the indicated point in Exercises

$f (x) = \left\{\begin{matrix} kx +1 & if x \leq 5 \\ 3x-5 & if x > 5 \end{matrix}\right. \: \: at x = 5$

Answer:

Given function is
$f (x) = \left\{\begin{matrix} kx +1 & if x \leq 5 \\ 3x-5 & if x > 5 \end{matrix}\right.$
When x = 5
For the function to be continuous
f(5) = R.H.L. = LH.L.
$f(5) = 5k+1\\ \lim_{x\rightarrow 5^-}f(x)= 5k+1\\ \lim_{x\rightarrow 5^+}f(x) = 3(5)-5 = 15-5=10\\ f(5) = \lim_{x\rightarrow 5^-}f(x) = \lim_{x\rightarrow 5^+}f(x)\\ 5k+1 = 10\\ k = \frac{9}{5}$
Hence, the values of k so that the function f is continuous at x= 5 is $\frac{9}{5}$

Question:30 Find the values of a and b such that the function defined by
$f (x) = \left\{\begin{matrix} 5 & if\: \: x \leq 2 \\ ax + b & if\: \: 2 < x < 10 \\ 21 , & if\: \: x > 10 \end{matrix}\right.$
is a continuous function.

Answer:

Given continuous function is
$f (x) = \left\{\begin{matrix} 5 & if\: \: x \leq 2 \\ ax + b & if\: \: 2 < x < 10 \\ 21 , & if\: \: x > 10 \end{matrix}\right.$
The function is continuous so
$\lim_{x\rightarrow 2^-}f(x) = \lim_{x\rightarrow 2^+}f(x)\\ and\\ \lim_{x\rightarrow 10^-}f(x)=\lim_{x\rightarrow 10^+}f(x)$
$\lim_{x\rightarrow 2^-}f(x) = 5\\ \lim_{x\rightarrow 2^+}f(x)=ax+b=2a+b\\ 2a+b = 5 \ \ \ \ \ \ \ \ \ \ \ -(i)\\ and\\ \lim_{x\rightarrow 10^-}f(x)=ax+b=10a+b\\ \lim_{x\rightarrow 10^+}f(x)=21\\ 10a+b=21 \ \ \ \ \ \ \ \ -(ii)$
By solving equation (i) and (ii)
a = 2 and b = 1
Hence, values of a and b such that the function defined by $f (x) = \left\{\begin{matrix} 5 & if\: \: x \leq 2 \\ ax + b & if\: \: 2 < x < 10 \\ 21 , & if\: \: x > 10 \end{matrix}\right.$ is a continuous function is 2 and 1 respectively

Question:31. Show that the function defined by $f (x) = \cos (x^2 )$ is a continuous function.

Answer:

Given function is
$f (x) = \cos (x^2 )$
given function is defined for all real values of x
Let x = k + h
if $x\rightarrow k , \ then \ h \rightarrow 0$
$f(k) = \cos k^2\\ \lim_{x \rightarrow k}f(x) = \lim_{x \rightarrow k}\cos x^2 = \lim_{h \rightarrow 0}\cos (k+h)^2 = \cos k^2\\ \lim_{x \rightarrow k}f(x) = f(k)$
Hence, the function $f (x) = \cos (x^2 )$ is a continuous function

Question:32. Show that the function defined by $f (x) = |\cos x |$ is a continuous function.

Answer:

Given function is
$f (x) = |\cos x |$
given function is defined for all values of x
f = g o h , g(x) = |x| and h(x) = cos x
Now,
$g(x)\begin{cases} -x & \text{ if } x<0 \\ 0 & \text{ if } x= 0\\ x& \text{ if } x>0 \end{cases}$
g(x) is defined for all real numbers k
case(i) k < 0
$g(k) = -k\\ \lim_{x\rightarrow k}g(x) = -k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k < 0

case (ii) k > 0
$g(k) = k\\ \lim_{x\rightarrow k}g(x) = k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k > 0

case (iii) k = 0
$g(0) = 0\\ \lim_{x\rightarrow 0^-}g(x) = -x = 0\\ \lim_{x\rightarrow 0^+}g(x ) = x = 0\\ \lim_{x\rightarrow 0^-}g(x) = g(0) = \lim_{x\rightarrow 0^+}g(x )$
Hence, g(x) is continuous when k = 0
Therefore, g(x) = |x| is continuous for all real values of x
Now,
h(x) = cos x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \cos c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\cos x = \lim_{h\rightarrow 0}\cos (c+h)\\ We \ know \ that\\ \cos(a+b) = \cos a \cos b + \sin a\sin b\\ \lim_{h\rightarrow 0}\cos (c+h) = \lim_{h\rightarrow 0}(\cos c\cos h + \sin c \sin h) = \lim_{h\rightarrow 0}\cos c\cos h + \lim_{h\rightarrow 0}\sin c \sin h$
$=\cos c\cos 0 + \sin c \sin 0 = \cos c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, function $h(x) = \cos x$ is a continuous function
g(x) is continuous , h(x) is continuous
Therefore, f(x) = g o h is also continuous

Question:33 . Examine that sin | x| is a continuous function.

Answer:

Given function is
f(x) = sin |x|
f(x) = h o g , h(x) = sin x and g(x) = |x|
Now,

$g(x)\begin{cases} -x & \text{ if } x<0 \\ 0 & \text{ if } x= 0\\ x& \text{ if } x>0 \end{cases}$
g(x) is defined for all real numbers k
case(i) k < 0
$g(k) = -k\\ \lim_{x\rightarrow k}g(x) = -k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k < 0

case (ii) k > 0
$g(k) = k\\ \lim_{x\rightarrow k}g(x) = k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k > 0

case (iii) k = 0
$g(0) = 0\\ \lim_{x\rightarrow 0^-}g(x) = -x = 0\\ \lim_{x\rightarrow 0^+}g(x ) = x = 0\\ \lim_{x\rightarrow 0^-}g(x) = g(0) = \lim_{x\rightarrow 0^+}g(x )$
Hence, g(x) is continuous when k = 0
Therefore, g(x) = |x| is continuous for all real values of x
Now,
h(x) = sin x
Let suppose x = c + h
if $x \rightarrow c , \ then \ h \rightarrow 0$
$h(c) = \sin c\\ \lim_{x\rightarrow c}h(x) = \lim_{x\rightarrow c}\sin x = \lim_{h\rightarrow 0}\sin (c+h)\\ We \ know \ that\\ \sin(a+b) = \sin a \cos b + \cos a\sin b\\ \lim_{h\rightarrow 0}\sin (c+h) = \lim_{h\rightarrow 0}(\sin c\cos h + \cos c \sin h) = \lim_{h\rightarrow 0}\sin c\cos h + \lim_{h\rightarrow 0}\cos c \sin h$
$=\sin c\cos 0 + \cos c \sin 0 = \sin c$
$\lim_{x\rightarrow c}h(x) = h(c)$
Hence, function $h(x) = \sin x$ is a continuous function
g(x) is continuous , h(x) is continuous
Therefore, f(x) = h o g is also continuous

Question:34. Find all the points of discontinuity of f defined by $f (x) = | x| - | x + 1|.$

Answer:

Given function is
$f (x) = | x| - | x + 1|$
Let g(x) = |x| and h(x) = |x+1|
Now,
$g(x)\begin{cases} -x & \text{ if } x<0 \\ 0 & \text{ if } x= 0\\ x& \text{ if } x>0 \end{cases}$
g(x) is defined for all real numbers k
case(i) k < 0
$g(k) = -k\\ \lim_{x\rightarrow k}g(x) = -k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k < 0

case (ii) k > 0
$g(k) = k\\ \lim_{x\rightarrow k}g(x) = k\\ \lim_{x\rightarrow k}g(x) = g(k)$
Hence, g(x) is continuous when k > 0

case (iii) k = 0
$g(0) = 0\\ \lim_{x\rightarrow 0^-}g(x) = -x = 0\\ \lim_{x\rightarrow 0^+}g(x ) = x = 0\\ \lim_{x\rightarrow 0^-}g(x) = g(0) = \lim_{x\rightarrow 0^+}g(x )$
Hence, g(x) is continuous when k = 0
Therefore, g(x) = |x| is continuous for all real values of x

Now,
$h(x)\begin{cases} -(x+1) & \text{ if } x<-1 \\ 0 & \text{ if } x= -1\\ (x+1)& \text{ if } x>-1 \end{cases}$
g(x) is defined for all real numbers k
case(i) k < -1
$h(k) = -(k+1)\\ \lim_{x\rightarrow k}h(x) = -(k+1)\\ \lim_{x\rightarrow k}h(x) = h(k)$
Hence, h(x) is continuous when k < -1

case (ii) k > -1
$h(k) = k+1\\ \lim_{x\rightarrow k}h(x) = k+1\\ \lim_{x\rightarrow k}h(x) = h(k)$
Hence, h(x) is continuous when k > -1

case (iii) k = -1
$h(-1) = 0\\ \lim_{x\rightarrow -1^-}h(x) = -(x-1) = 0\\ \lim_{x\rightarrow -1^+}h(x ) = x+1 = 0\\ \lim_{x\rightarrow -1^-}h(x) = h(0) = \lim_{x\rightarrow -1^+}h(x )$
Hence, h(x) is continuous when k = -1
Therefore, h(x) = |x+1| is continuous for all real values of x
g(x) is continuous and h(x) is continuous
Therefore, f(x) = g(x) - h(x) = |x| - |x+1| is also continuous

NCERT class 12 maths chapter 5 question answer: Excercise: 5.2

Question:1. Differentiate the functions with respect to x in

$\sin (x^2 +5 )$

Answer:

Given function is
$f(x)=\sin (x^2 +5 )$
when we differentiate it w.r.t. x.
Lets take $t = x^2+5$ . then,
$f(t) = \sin t$
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx}$ (By chain rule)
$\frac{df(t)}{dt} = \frac{d(\sin t )}{dt} = \cos t = \cos (x^2+5)$
$\frac{dt}{dx} = \frac{d(x^2+5 )}{dx} = 2x$
Now,
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx} = \cos (x^2+5).2x$
Therefore, the answer is $2x \cos (x^2+5)$

Question:2. Differentiate the functions with respect to x in

$\cos ( \sin x )$

Answer:

Given function is
$f(x)= \cos ( \sin x )$
Lets take $t = \sin x$ then,
$f(t) = \cos t$
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx}$ ( By chain rule)
$\frac{df(t)}{dt} = \frac{d(\cos t)}{dt} = -\sin t = -\sin (\sin x)$
$\frac{dt}{dx} = \frac{d(\sin x)}{dt} = \cos x$
Now,
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx} = -\sin(\sin x).\cos x$
Therefore, the answer is $-\sin(\sin x).\cos x$

Question:3. Differentiate the functions with respect to x in

$\sin (ax +b )$

Answer:

Given function is
$f(x) = \sin (ax +b )$
when we differentiate it w.r.t. x.
Lets take $t = ax+b$ . then,
$f(t) = \sin t$
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx}$ (By chain rule)
$\frac{df(t)}{dt} = \frac{d(\sin t )}{dt} = \cos t = \cos (ax+b)$
$\frac{dt}{dx} = \frac{d(ax+b )}{dx} = a$
Now,
$\frac{df(t)}{dx} = \frac{df(t)}{dt}.\frac{dt}{dx} = \cos (ax+b).a$
Therefore, the answer is $a \cos (ax+b)$

Question:4 . Differentiate the functions with respect to x in

$\sec (\tan (\sqrt x) )$

Answer:

Given function is
$f(x)=\sec (\tan (\sqrt x) )$
when we differentiate it w.r.t. x.
Lets take $t = \sqrt x$ . then,
$f(t) = \sec (\tan t)$
take $\tan t = k$ . then,
$f(k) = \sec k$
$\frac{df(k)}{dx} = \frac{df(k)}{dk}.\frac{dk}{dt}.\frac{dt}{dx}$ (By chain rule)
$\frac{df(k)}{dk} = \frac{d(\sec k )}{dk} = \sec k \tan k = \sec(\tan\sqrt x)\tan(\tan\sqrt x)$
$(\because k = \tan t \ and \ t = \sqrt x)$
$\frac{df(t)}{dt} = \frac{d(\tan t )}{dt} = \sec^2 t =\sec^2 (\sqrt x) \ \ \ \ \ \ (\because t = \sqrt x)$
$\frac{dt}{dx} = \frac{d(\sqrt x)}{dx} = \frac{1}{2\sqrt x}$
Now,
$\frac{df(k)}{dx} = \frac{df(k)}{dk}.\frac{dk}{dt}.\frac{dt}{dx} =\sec(\tan \sqrt x)\tan(\tan \sqrt x).\sec^2 (\sqrt x) . \frac{1}{2\sqrt x}$
Therefore, the answer is $\frac{\sec(\tan \sqrt x).\tan(\tan \sqrt x).\sec^2 (\sqrt x)}{2\sqrt x}$

Question:5. Differentiate the functions with respect to x in

$\frac{\sin (ax +b )}{\cos (cx + d)}$

Answer:

Given function is
$f(x) = \frac{\sin (ax +b )}{\cos (cx + d)} = \frac{g(x)}{h(x)}$
We know that,
$f^{'}(x) = \frac{g^{'}(x)h(x)-g(x)h^{'}(x)}{h^2(x)}$
$g(x) = \sin(ax+b)$ and $h(x) = \cos(cx+d)$
Lets take $u = (ax+b) \ and \ v = (cx+d)$
Then,
$\sin (ax+b) = \sin u \ and \ \cos(cx+d) = \cos c$
$g^{'}(x)=\frac{d(g(x))}{dx} = \frac{d(g(x))}{du}.\frac{du}{dx}$ (By chain rule)
$\frac{d(g(x))}{du} = \frac{d(\sin u)}{du} = \cos u = \cos(ax+b) \ \ \ \ \ \ \ \ \ (\because u = ax +b)$
$\frac{du}{dx} = \frac{d(ax+b)}{dx} = a$
$g^{'}(x)=a\cos (ax+b)$ -(i)
Similarly,
$h^{'}(x)=\frac{d(h(x))}{dx} = \frac{d(h(x))}{dv}.\frac{dv}{dx}$
$\frac{d(h(x))}{dv}= \frac{d(\cos v)}{dv} = -\sin v = -\sin (cx+d) \ \ \ \ \ \ \ (\because v = (cx+d))$
$\frac{dv}{dx}= \frac{d(cx+d)}{dv} = c$
$h^{'}(x)=-c\sin(cx+d)$ -(ii)
Now, put (i) and (ii) in
$f^{'}(x) = \frac{g^{'}(x)h(x)-g(x)h^{'}(x)}{h^2(x)} = \frac{a\cos(ax+b).\cos(cx+d)-\sin(ax+b).(-c.\sin(cx+d))}{\cos^2(cx+d)}$
$= \frac{a\cos(ax+b).\cos(cx+d)}{\cos^2(cx+d)}+\frac{\sin(ax+b).c.\sin(cx+d)}{\cos^2(cx+d)}$
$= a\cos(ax+b).\sec(cx+d) +c\sin(ax+b).\tan(cx+d).\sec(cx+d)$
Therefore, the answer is $a\cos(ax+b).\sec(cx+d) +c\sin(ax+b).\tan(cx+d).\sec(cx+d)$

Question:6. Differentiate the functions with respect to x in

$\cos x^3 . \sin ^ 2 ( x ^5 )$

Answer:

Given function is
$f(x)=\cos x^3 . \sin ^ 2 ( x ^5 )$
Differentitation w.r.t. x is
$f^{'}(x) = g^{'}(x).h(x) + g(x).h^{'}(x)$
$g(x) = \cos x^3 \ and \ h(x) = sin^2(x^5)$
Lets take $u = x^3 \ and \ v = x^5$
Our functions become,
$\cos x^3 = \cos u$ and $\sin^2(x^5) = \sin^2v$
Now,
$g^{'}(x) = \frac{d(g(x))}{dx} =\frac{d(g(u))}{du}.\frac{du}{dx}$ ( By chain rule)
$\frac{d(g(u))}{du} = \frac{d(\cos u)}{du} = -\sin u =- \sin x^3 \ \ \ \ (\because u = x^3)$
$\frac{du}{dx} = \frac{d(x^3)}{dx} = 3x^2$
$g^{'}(x) = -\sin x^3.3x^2$ -(i)
Similarly,
$h^{'}(x) = \frac{d(h(x))}{dx} =\frac{d(h(v))}{dv}.\frac{dv}{dx}$
$\frac{d(h(v))}{dv}= \frac{d(\sin^2v)}{dv} =2\sin v \cos v =2\sin x^5\cos x^5 \ \ \ (\because v = x^5)$

$\frac{dv}{dx} = \frac{d(x^5)}{dx} = 5x^4$
$h^{'}(x) = 2\sin x^5\cos x^5.5x^4 = 10x^4\sin x^5\cos x^5$ -(ii)
Put (i) and (ii) in
$f^{'}(x) = g^{'}(x).h(x) + g(x).h^{'}(x) = -3x^2\sin x^3.\sin^2 x^5+\cos x^3.10x^4\sin x^5\cos x^5$
Therefore, the answer is $10x^4\sin x^5\cos x^5.\cos x^3 -3x^2\sin x^3.\sin^2 x^5$

Question:7. Differentiate the functions with respect to x in

$2 \sqrt { \cot ( x^2 )}$

Answer:

Give function is
$f(x)=2 \sqrt { \cot ( x^2 )}$
Let's take $t = x^2$
Now, take $\cot t = k^2$
$f(k) = 2k$
Differentiation w.r.t. x
$\frac{d(f(k))}{dx} = \frac{d(f(k))}{dk}.\frac{dk}{dt}.\frac{dt}{dx}$ -(By chain rule)
$\frac{d(f(k))}{dk} = \frac{d(2k)}{dk} = 2$
$\frac{dk}{dt} = \frac{d(\sqrt{\cot t})}{dt} = \frac{1}{2\sqrt{cot t}}.(-cosec^2 t) = \frac{-cosec^2 x^2}{2\sqrt{cot x^2}} \ \ \ (\because t = x^2)$
$\frac{dt}{dx} = \frac{d(x^2)}{dx} = 2x$
So,
$\frac{d(f(k))}{dx} = 2.\frac{-cosec^2 x^2}{2\sqrt{cot x^2}}.2x = \frac{-2\sqrt2x}{\sin^2x^2\sqrt{\frac{2\sin x^2\cos x^2}{\sin^2x^2}} }$ ( Multiply and divide by $\sqrt 2$ and multiply and divide $\sqrt {\cot x^2}$ by $\sqrt{\sin x^2$ )
$(\because \cot x = \frac{\cos x}{\sin x} \ and \ cosec x = \frac{1}{\sin x } )$
$=\frac{-2\sqrt2x}{\sin x^2\sqrt{\sin2x^2}} \ \ \ \ (\because 2\sin x\cos x=\sin2x)$
There, the answer is $\frac{-2\sqrt2x}{\sin x^2\sqrt{\sin2x^2}}$

Question:8 Differentiate the functions with respect to x in

$\cos ( \sqrt x )$

Answer:

Let us assume : $y\ =\ \cos ( \sqrt x )$

Differentiating y with respect to x, we get :

$\frac{dy}{dx}\ =\ \frac{d(\cos ( \sqrt x ))}{dx}$

or $=\ - \sin \sqrt{x}.\frac{d( \sqrt x )}{dx}$

or $=\ \frac{- \sin \sqrt{x}}{2\sqrt{x}}$

Question:9 . Prove that the function f given by $f (x) = |x-1 | , x \epsilon R$ is not differentiable at x = 1.

Answer:

Given function is
$f (x) = |x-1 | , x \epsilon R$
We know that any function is differentiable when both
$\lim_{h\rightarrow 0^-}\frac{f(c+h)-f(c)}{h}$ and $\lim_{h\rightarrow 0^+}\frac{f(c+h)-f(c)}{h}$ are finite and equal
Required condition for function to be differential at x = 1 is

$\lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^+}\frac{f(1+h)-f(1)}{h}$
Now, Left-hand limit of a function at x = 1 is
$\lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^-}\frac{|1+h-1|-|1-1|}{h} = \lim_{h\rightarrow 0^-}\frac{|h|-0}{h}$
$= \lim_{h\rightarrow 0^-}\frac{-h}{h} = -1 \ \ \ \ (\because h < 0)$
Right-hand limit of a function at x = 1 is
$\lim_{h\rightarrow 0^+}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^+}\frac{|1+h-1|-|1-1|}{h} = \lim_{h\rightarrow 0^+}\frac{|h|-0}{h}$
$=\lim_{h\rightarrow 0^-}\frac{h}{h} = 1$
Now, it is clear that
R.H.L. at x= 1 $\neq$ L.H.L. at x= 1
Therefore, function $f (x) = |x-1 |$ is not differentiable at x = 1

Question:10. Prove that the greatest integer function defined by $f (x) = [x] , 0 < x < 3$ is not differentiable at

x = 1 and x = 2.

Answer:

Given function is
$f (x) = [x] , 0 < x < 3$
We know that any function is differentiable when both
$\lim_{h\rightarrow 0^-}\frac{f(c+h)-f(c)}{h}$ and $\lim_{h\rightarrow 0^+}\frac{f(c+h)-f(c)}{h}$ are finite and equal
Required condition for function to be differential at x = 1 is

$\lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^+}\frac{f(1+h)-f(1)}{h}$
Now, Left-hand limit of the function at x = 1 is
$\lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^-}\frac{[1+h]-[1]}{h} = \lim_{h\rightarrow 0^-}\frac{0-1}{h}$
$=\lim_{h\rightarrow 0^-}\frac{-1}{h} = -\infty \ \ \ \ \ (\because h < 0 \Rightarrow 1+h<1, \therefore [1+h] =0)$
Right-hand limit of the function at x = 1 is
$\lim_{h\rightarrow 0^+}\frac{f(1+h)-f(1)}{h } = \lim_{h\rightarrow 0^+}\frac{[1+h]-[1]}{h} = \lim_{h\rightarrow 0^+}\frac{1-1}{h}$
$=\lim_{h\rightarrow 0^-}\frac{0}{h} = 0 \ \ \ \ \ (\because h > 0 \Rightarrow 1+h>1, \therefore [1+h] =1)$
Now, it is clear that
R.H.L. at x= 1 $\neq$ L.H.L. at x= 1 and L.H.L. is not finite as well
Therefore, function $f(x) = [x]$ is not differentiable at x = 1
Similary, for x = 2
Required condition for function to be differential at x = 2 is

$\lim_{h\rightarrow 0^-}\frac{f(2+h)-f(2)}{h } = \lim_{h\rightarrow 0^+}\frac{f(2+h)-f(2)}{h}$
Now, Left-hand limit of the function at x = 2 is
$\lim_{h\rightarrow 0^-}\frac{f(2+h)-f(2)}{h } = \lim_{h\rightarrow 0^-}\frac{[2+h]-[2]}{h} = \lim_{h\rightarrow 0^-}\frac{1-2}{h}$
$=\lim_{h\rightarrow 0^-}\frac{-1}{h} = -\infty \ \ \ \ (\because h < 0 \Rightarrow 2+h<2, \therefore [2+h] =1)$
Right-hand limit of the function at x = 1 is
$\lim_{h\rightarrow 0^+}\frac{f(2+h)-f(2)}{h } = \lim_{h\rightarrow 0^+}\frac{[2+h]-[2]}{h} = \lim_{h\rightarrow 0^+}\frac{2-2}{h}$
$=\lim_{h\rightarrow 0^-}\frac{0}{h} = 0 \ \ \ \ \ (\because h > 0 \Rightarrow 2+h>2, \therefore [2+h] =2)$
Now, it is clear that
R.H.L. at x= 2 $\neq$ L.H.L. at x= 2 and L.H.L. is not finite as well
Therefore, function $f(x) = [x]$ is not differentiable at x = 2

NCERT class 12 maths chapter 5 question answer: Exercise: 5.3

Question:1. Find dy/dx in the following:

$2 x + 3 y = \sin x$

Answer:

Given function is
$2 x + 3 y = \sin x$
We can rewrite it as
$3y = \sin x - 2x$
Now, differentiation w.r.t. x is
$3\frac{dy}{dx} = \frac{d(\sin x - 2x)}{dx} = \cos x - 2$
$\frac{dy}{dx} = \frac{\cos x-2}{3}$
Therefore, the answer is $\frac{\cos x-2}{3}$

Question:2. Find dy/dx in the following: $2 x + 3y = \sin y$

Answer:

Given function is
$2 x + 3 y = \sin y$
We can rewrite it as
$\sin y - 3y = 2x$
Now, differentiation w.r.t. x is
$\frac{dy}{dx}(\sin y - 3y) = \frac{d( 2x)}{dx}$

$(\cos y\frac{dy}{dx} - 3\frac{dy}{dx}) = 2$
$\frac{dy}{dx} = \frac{2}{\cos y -3}$
Therefore, the answer is $\frac{2}{\cos y -3}$

Question:3. Find dy/dx in the following: $ax + by ^2 = \cos y$

Answer:

Given function is
$ax + by ^2 = \cos y$
We can rewrite it as
$by^2-\cos y = -ax$
Now, differentiation w.r.t. x is
$\frac{dy}{dx}(2by - (-\sin y)) = \frac{d( -ax)}{dx} = -a$
$\frac{dy}{dx} = \frac{-a}{2b y +\sin y}$
Therefore, the answer is $\frac{-a}{2b y +\sin y}$

Question:4. Find dy/dx in the following:

$xy + y^2 = \tan x + y$

Answer:

Given function is
$xy + y^2 = \tan x + y$
We can rewrite it as
$xy+y^2-y= \tan x$
Now, differentiation w.r.t. x is
$y+\frac{dy}{dx}(x+2y-1) = \frac{d( \tan x)}{dx} = \sec^2 x$
$\frac{dy}{dx} = \frac{\sec^2 x- y}{x+2y-1}$
Therefore, the answer is $\frac{\sec^2 x- y}{x+2y-1}$

Question:5. Find dy/dx in the following: $x^2 + xy + y^2 = 100$

Answer:

Given function is
$x^2 + xy + y^2 = 100$
We can rewrite it as
$xy + y^2 = 100 - x^2$
Now, differentiation w.r.t. x is
$y+\frac{dy}{dx}(x+2y) = \frac{d( 100-x^2)}{dx} = -2x$
$\frac{dy}{dx} = \frac{-2 x- y}{x+2y}$
Therefore, the answer is $\frac{-2 x- y}{x+2y}$

Question:6 Find dy/dx in the following:

$x ^3 + x^2 y + xy^2 + y^3 = 81$

Answer:

Given function is
$x ^3 + x^2 y + xy^2 + y^3 = 81$
We can rewrite it as
$x^2 y + xy^2 + y^3 = 81 - x^3$
Now, differentiation w.r.t. x is
$\frac{d(x^2 y + xy^2 + y^3)}{dx} = \frac{d(81 - x^3)}{dx}$
$2xy+y^2+\frac{dy}{dx}(x^2+2xy+3y^2) = -3x^2\\ \frac{dy}{dx}=\frac{-(3x^2+2xy+y^2)}{(x^2+2xy+3y^2}$
Therefore, the answer is $\frac{-(3x^2+2xy+y^2)}{(x^2+2xy+3y^2}$

Question:7 . Find dy/dx in the following: $\sin ^ 2 y + \cos xy = k$

Answer:

Given function is
$\sin ^ 2 y + \cos xy = k$
Now, differentiation w.r.t. x is
$\frac{d(\sin^2y+\cos xy)}{dx} = \frac{d(k)}{dx}$
$2\sin y \cos y\frac{dy}{dx}+(-\sin xy)(y+x\frac{dy}{dx})=0\\ \frac{dy}{dx}(2\sin y \cos y-x\sin xy)= y\sin xy\\ \frac{dy}{dx} = \frac{y\sin xy}{2\sin y \cos y-x\sin xy} = \frac{y\sin xy}{\sin 2y -x\sin xy} \ \ \ \ \ \ (\because 2\sin x\cos y = \sin 2x)$
Therefore, the answer is $\frac{y\sin xy}{\sin 2y -x\sin xy}$

Question:8. Find dy/dx in the following:

$\sin ^2 x + \cos ^ 2 y = 1$

Answer:

Given function is
$\sin ^2 x + \cos ^ 2 y = 1$
We can rewrite it as
$\cos ^ 2 y = 1-\sin^2x$
Now, differentiation w.r.t. x is
$\frac{d(\cos^2y)}{dx} = \frac{d(1-\sin^2x)}{dx}$
$2\cos y (-\sin y)\frac{dy}{dx} = -2\sin x \cos x\\ \frac{dy}{dx} = \frac{2\sin x\cos x}{2\sin y \cos y} = \frac{\sin 2x }{\sin 2y} \ \ \ \ \ \ (\because2\sin a \cos a = \sin 2a)$
Therefore, the answer is $\frac{\sin 2x}{\sin 2y }$

Question:9 Find dy/dx in the following:

$y = \sin ^{-1} \left ( \frac{2x}{1+ x^2 } \right )$

Answer:

Given function is
$y = \sin ^{-1} \left ( \frac{2x}{1+ x^2 } \right )$
Lets consider $x = \tan t$
Then,
$\frac{d(x)}{dx} = \frac{d(\tan t)}{dt}.\frac{dt}{dx} \ \ \ \ \ \ \ \ \ (by \ chain \ rule)$
$1 = \sec^2 t . \frac{dt}{dx}\\ \frac{dt}{dx} = \frac{1}{\sec^2t} = \frac{1}{1+\tan ^2t} = \frac{1}{1+x^2}\ \ \ \ \ \ \ (\because \sec^2t=1+\tan^2t \ and \ x = \tan t)$
Now,
$\frac{2x}{1+x^2} = \frac{2\tan t }{1+\tan^2t} = \sin 2t \ \ \ \ \ \ (\because \sin 2x = \frac{2\tan x }{1+\tan^2 x})$
Our equation reduces to
$y = \sin^{-1}(\sin 2t)$
$y = 2t$
Now, differentiation w.r.t. x is
$\frac{d(y)}{dx} = \frac{d(2t)}{dt}.\frac{dt}{dx}$
$\frac{dy}{dx} = 2.\frac{1}{1+x^2} = \frac{2}{1+x^2}$
Therefore, the answer is $\frac{2}{1+x^2}$

Question:10. Find dy/dx in the following:
$y = \tan ^{-1} \left ( \frac{3x- x ^3}{1- 3x ^2} \right ) , - \frac{1}{\sqrt 3 } < x < \frac{1}{\sqrt 3 }$

Answer:

Given function is
$y = \tan ^{-1} \left ( \frac{3x- x ^3}{1- 3x ^2} \right )$
Lets consider $x = \tan t$
Then,
$\frac{d(x)}{dx} = \frac{d(\tan t)}{dt}.\frac{dt}{dx} \ \ \ \ \ \ \ \ \ (by \ chain \ rule)$
$1 = \sec^2 t . \frac{dt}{dx}\\ \frac{dt}{dx} = \frac{1}{\sec^2t} = \frac{1}{1+\tan ^2t} = \frac{1}{1+x^2}\ \ \ \ \ \ \ (\because \sec^2t=1+\tan^2t \ and \ x = \tan t)$
Now,
$\frac{3x-x^3}{1-3x^2} = \frac{3\tan t-\tan^3t }{1-3\tan^2t} = \tan3t \ \ \ \ \ \ (\because \tan 3x = \frac{3\tan x-\tan^3x }{1-3\tan^2x} )$
Our equation reduces to
$y = \tan^{-1}(\tan 3t)$
$y = 3t$
Now, differentiation w.r.t. x is
$\frac{d(y)}{dx} = \frac{d(3t)}{dt}.\frac{dt}{dx}$
$\frac{dy}{dx} = 3.\frac{1}{1+x^2} = \frac{3}{1+x^2}$
Therefore, the answer is $\frac{3}{1+x^2}$

Question:11. Find dy/dx in the following:

$y = \cos ^{-1} \left ( \frac{1 - x^2 }{1+ x^2 } \right ) , 0 < x < 1$

Answer:

Given function is
$y = \cos ^{-1} \left ( \frac{1 - x^2 }{1+ x^2 } \right )$
Let's consider $x = \tan t$
Then,
$\frac{d(x)}{dx} = \frac{d(\tan t)}{dt}.\frac{dt}{dx} \ \ \ \ \ \ \ \ \ (by \ chain \ rule)$
$1 = \sec^2 t . \frac{dt}{dx}\\ \frac{dt}{dx} = \frac{1}{\sec^2t} = \frac{1}{1+\tan ^2t} = \frac{1}{1+x^2}\ \ \ \ \ \ \ (\because \sec^2t=1+\tan^2t \ and \ x = \tan t)$
Now,
$\frac{1-x^2}{1+x^2} = \frac{1-\tan^2t }{1+\tan^2t} = \cos 2t \ \ \ \ \ \ (\because \cos 2x = \frac{1-\tan^2x }{1+\tan^2x} )$
Our equation reduces to
$y = \cos^{-1}(\cos 2t)$
$y = 2t$
Now, differentiation w.r.t. x is
$\frac{d(y)}{dx} = \frac{d(2t)}{dt}.\frac{dt}{dx}$
$\frac{dy}{dx} = 2.\frac{1}{1+x^2} = \frac{2}{1+x^2}$
Therefore, the answer is $\frac{2}{1+x^2}$

Question:12 . Find dy/dx in the following: $y = \sin ^{-1 } \left ( \frac{1- x ^2 }{1+ x^2} \right ) , 0< x < 1$

Answer:

Given function is
$y = \sin ^{-1} \left ( \frac{1 - x^2 }{1+ x^2 } \right )$
We can rewrite it as
$\sin y = \ \left ( \frac{1 - x^2 }{1+ x^2 } \right )$
Let's consider $x = \tan t$
Then,
$\frac{d(x)}{dx} = \frac{d(\tan t)}{dt}.\frac{dt}{dx} \ \ \ \ \ \ \ \ \ (by \ chain \ rule)$
$1 = \sec^2 t . \frac{dt}{dx}\\ \frac{dt}{dx} = \frac{1}{\sec^2t} = \frac{1}{1+\tan ^2t} = \frac{1}{1+x^2}\ \ \ \ \ \ \ (\because \sec^2t=1+\tan^2t \ and \ x = \tan t)$
Now,
$\frac{1-x^2}{1+x^2} = \frac{1-\tan^2t }{1+\tan^2t} = \cos 2t \ \ \ \ \ \ (\because \cos 2x = \frac{1-\tan^2x }{1+\tan^2x} )$
Our equation reduces to
$\sin y = \cos 2t$
Now, differentiation w.r.t. x is
$\frac{d(\sin y)}{dx} = \frac{d(\cos2t)}{dt}.\frac{dt}{dx}$
$\cos y\frac{dy}{dx} = 2(-\sin 2t).\frac{1}{1+x^2} = \frac{-2\sin2t}{1+x^2}$ $= \frac{-2.\frac{2\tan t}{1+\tan^2t}}{1+x^2} =\frac{-2.\frac{2x}{1+x^2}}{1+x^2} =\frac{-4x}{(1+x^2)^2}$
$(\because \sin 2x = \frac{2\tan x}{1+\tan^2x} \ and \ x = \tan t)$
$\sin y = \ \left ( \frac{1 - x^2 }{1+ x^2 } \right )\Rightarrow \cos y = \frac{2x}{1+x^2}$
$\frac{2x}{1+x^2}\frac{dy}{dx} = \frac{-4x}{(1+x^2)^2}$
$\frac{dy}{dx} = \frac{-2}{(1+x^2)}$
Therefore, the answer is $\frac{-2}{1+x^2}$

Question:13. Find dy/dx in the following:

$y = \cos ^{-1} \left ( \frac{2x}{1+ x^2 } \right ) , -1 < x < 1$

Answer:

Given function is
$y = \cos ^{-1} \left ( \frac{2x}{1+ x^2 } \right )$
We can rewrite it as
$\cos y = \left ( \frac{2x}{1+ x^2 } \right )$
Let's consider $x = \tan t$
Then,
$\frac{d(x)}{dx} = \frac{d(\tan t)}{dt}.\frac{dt}{dx} \ \ \ \ \ \ \ \ \ (by \ chain \ rule)$
$1 = \sec^2 t . \frac{dt}{dx}\\ \frac{dt}{dx} = \frac{1}{\sec^2t} = \frac{1}{1+\tan ^2t} = \frac{1}{1+x^2}\ \ \ \ \ \ \ (\because \sec^2t=1+\tan^2t \ and \ x = \tan t)$
Now,
$\frac{2x}{1+x^2} = \frac{2\tan t }{1+\tan^2t} = \sin 2t \ \ \ \ \ \ (\because \sin 2x = \frac{2\tan x }{1+\tan^2x} )$
Our equation reduces to
$\cos y = \sin 2t$
Now, differentiation w.r.t. x is
$\frac{d(\cos y)}{dx} = \frac{d(\sin2t)}{dt}.\frac{dt}{dx}$
$(-\sin y)\frac{dy}{dx} = 2(\cos 2t).\frac{1}{1+x^2} = \frac{2\cos2t}{1+x^2}$ $= \frac{2.\frac{1-\tan^2 t}{1+\tan^2t}}{1+x^2} =\frac{2.\frac{1-x^2}{1+x^2}}{1+x^2} =\frac{2(1-x^2)}{(1+x^2)^2}$
$(\because \cos 2x = \frac{1-\tan^2 x}{1+\tan^2x} \ and \ x = \tan t)$
$\cos y = \ \left ( \frac{2 x }{1+ x^2 } \right )\Rightarrow \sin y = \frac{1-x^2}{1+x^2}$
$-\frac{1-x^2}{1+x^2}\frac{dy}{dx} = \frac{2(1-x^2)}{(1+x^2)^2}$
$\frac{dy}{dx} = \frac{-2}{(1+x^2)}$
Therefore, the answer is $\frac{-2}{1+x^2}$

Question:14 . Find dy/dx in the following:

$y = \sin ^ { -1 } ( 2x \sqrt {1- x^2} ) , -\frac{1}{\sqrt2} < x \frac{1}{\sqrt 2 }$

Answer:

Given function is
$y = \sin ^ { -1 } ( 2x \sqrt {1- x^2} )$
Lets take $x = \sin t$
Then,
$\frac{d(x)}{dx} = \frac{(\sin t)}{dt}.\frac{dt}{dx} \ \ \ \ \ (by \ chain \ rule)$
$1 =\cos t.\frac{dt}{dx}$
$\frac{dt}{dx} = \frac{1}{\cos t } = \frac{1}{\sqrt{1-\sin ^2t}} = \frac{1}{\sqrt{1-x^2}}$
$(\because \cos x = \sqrt{1-\sin^2x} \ and \ x = \sin t )$
And
$2x\sqrt{1-x^2} = 2\sin t \sqrt{1-\sin^2t} = 2\sin t \sqrt{\cos^2 t} = 2\sin t\cos t =\sin 2t$
$(\because \cos x = \sqrt{1-\sin^2x} \ and \ 2\sin x\cos x = \sin2x )$
Now, our equation reduces to
$y = \sin ^ { -1 } ( \sin 2t )$
$y = 2t$
Now, differentiation w.r.t. x
$\frac{d(y)}{dx} = \frac{d(2t)}{dt}.\frac{dt}{dx}$
$\frac{dy}{dx} = 2.\frac{1}{\sqrt{1-x^2}} = \frac{2}{\sqrt{1-x^2}}$
Therefore, the answer is $\frac{2}{\sqrt{1-x^2}}$

Question:15 . Find dy/dx in the following:

$y = \sec ^{-1} \left ( \frac{1}{2x ^2 -1} \right ) , 0 < x < 1/ \sqrt 2$

Answer:

Given function is
$y = \sec ^{-1} \left ( \frac{1}{2x ^2 -1} \right )$
Let's take $x = \cos t$
Then,
$\frac{d(x)}{dx} = \frac{(\cos t)}{dt}.\frac{dt}{dx} \ \ \ \ \ (by \ chain \ rule)$
$1 =-\sin t.\frac{dt}{dx}$
$\frac{dt}{dx} = \frac{-1}{\sin t } = \frac{-1}{\sqrt{1-\cos ^2t}} = \frac{-1}{\sqrt{1-x^2}}$
$(\because \sin x = \sqrt{1-\cos^2x} \ and \ x = \cos t )$
And
$\frac{1}{2x^2-1} =\frac{1}{2\cos^2 t - 1} = \frac{1}{\cos2t} = \sec2t$
$(\because \cos 2x = \sqrt{2\cos^2x-1} \ and \ \cos x = \frac{1}{\sec x} )$

Now, our equation reduces to
$y = \sec ^{-1} \left ( \sec 2t \right )$
$y = 2t$
Now, differentiation w.r.t. x
$\frac{d(y)}{dx} = \frac{d(2t)}{dt}.\frac{dt}{dx}$
$\frac{dy}{dx} = 2.\frac{-1}{\sqrt{1-x^2}} = \frac{-2}{\sqrt{1-x^2}}$
Therefore, the answer is $\frac{-2}{\sqrt{1-x^2}}$

NCERT class 12 maths chapter 5 question answer: Exercise 5.4

Question:1. Differentiate the following w.r.t. x:

$\frac{e ^x }{\sin x }$

Answer:

Given function is
$f(x)=\frac{e ^x }{\sin x }$
We differentiate with the help of Quotient rule
$f^{'}(x)=\frac{\frac{d(e^x)}{dx}.\sin x-e^x.\frac{(\sin x)}{dx} }{\sin^2 x }$
$=\frac{e^x.\sin x-e^x.\cos }{\sin^2 x } = \frac{e^x(\sin x-\cos x)}{\sin^2x}$
Therefore, the answer is $\frac{e^x(\sin x-\cos x)}{\sin^2x}$

Question:2 . Differentiate the following w.r.t. x:

$e ^{\sin ^{-1}x}$

Answer:

Given function is
$f(x)=e ^{\sin ^{-1}x}$
Let $g(x)={\sin ^{-1}x}$
Then,
$f(x)=e^{g(x)}$
Now, differentiation w.r.t. x
$f^{'}(x)=g^{'}(x).e^{g(x)}$ -(i)
$g(x) = \sin^{-1}x \Rightarrow g^{'}(x ) = \frac{1}{\sqrt{1-x^2}}$
Put this value in our equation (i)
$f^{'}(x) = \frac{1}{\sqrt{1-x^2}}.e^{\sin^{-1}x} = \frac{e^{\sin^{-1}x}}{\sqrt{1-x^2}}$

Question:3 . Differentiate the following w.r.t. x:

$e ^x^{ ^3}$

Answer:

Given function is
$f(x)=e ^{x^3}$
Let $g(x)=x^3$
Then,
$f(x)=e^{g(x)}$
Now, differentiation w.r.t. x
$f^{'}(x)=g^{'}(x).e^{g(x)}$ -(i)
$g(x) = x^3 \Rightarrow g^{'}(x ) =3x^2$
Put this value in our equation (i)
$f^{'}(x) =3x^2.e^{x^3}$
Therefore, the answer is $3x^2.e^{x^3}$

Question:4. Differentiate the following w.r.t. x:

$\sin ( \tan ^ { -1} e ^{-x })$

Answer:

Given function is
$f(x)=\sin ( \tan ^ { -1} e ^{-x })$
Let's take $g(x ) = \tan^{-1}e^{-x}$
Now, our function reduces to
$f(x) = \sin(g(x))$
Now,
$f^{'}(x) = g^{'}(x)\cos(g(x))$ -(i)
And
$g(x)=\tan^{-1}e^{-x}\\\Rightarrow g^{'}(x) = \frac{d(\tan^{-1}e^{-x})}{dx}.\frac{d(e^{-x})}{dx}= \frac{1}{1+(e^{-x})^2}.-e^{-x} = \frac{-e^{-x}}{1+e^{-2x}}$
Put this value in our equation (i)
$f^{'}(x) =\frac{-e^{-x}}{1+e^{-2x}}\cos(\tan^{-1}e^{-x})$
Therefore, the answer is $\frac{-e^{-x}}{1+e^{-2x}}\cos(\tan^{-1}e^{-x})$

Question:5 . Differentiate the following w.r.t. x:

$\log (\cos e ^x )$

Answer:

Given function is
$f(x)=\log (\cos e ^x )$
Let's take $g(x ) = \cos e^{x}$
Now, our function reduces to
$f(x) = \log(g(x))$
Now,
$f^{'}(x) = g^{'}(x).\frac{1}{g(x)}$ -(i)
And
$g(x)=\cos e^{x}\\\Rightarrow g^{'}(x) = \frac{d(\cos e^{x})}{dx}.\frac{d(e^{x})}{dx}= (-\sin e^x).e^{x} = -e^x.\sin e^x$
Put this value in our equation (i)
$f^{'}(x) =-e^x.\sin e^x.\frac{1}{\cos e^x} = -e^x.\tan e^x \ \ \ \ \ (\because \frac{\sin x}{\cos x}=\tan x)$
Therefore, the answer is $-e^x.\tan e^x,\ \ \ e^x\neq (2n+1)\frac{\pi}{2},\ \ n\in N$

Question:6 . Differentiate the following w.r.t. x:

$e ^x + e ^{x^2} + .....e ^{x^5}$

Answer:

Given function is
$f(x)= e ^x + e ^{x^2} + .....e ^{x^5}$
Now, differentiation w.r.t. x is
$f^{'}(x)= \frac{d(e^x)}{dx}.\frac{d(x)}{dx}+\frac{d(e^{x^2})}{dx}.\frac{d(x^2)}{dx}+\frac{d(e^{x^3})}{dx}.\frac{d(x^3)}{dx}+\frac{d(e^{x^4})}{dx}.\frac{d(x^4)}{dx}+\frac{d(e^{x^5})}{dx}.\frac{d(x^5)}{dx}$
$=e^x.1+e^{x^2}.2x+e^{x^3}.3x^2+e^{x^4}.4x^3+e^{x^5}.5x^4$
$=e^x+2xe^{x^2}+3x^2e^{x^3}+4x^3e^{x^4}+5x^4e^{x^5}$
Therefore, answer is $e^x+2xe^{x^2}+3x^2e^{x^3}+4x^3e^{x^4}+5x^4e^{x^5}$

Question:7 . Differentiate the following w.r.t. x:

$\sqrt { e ^{ \sqrt x }} , x > 0$

Answer:

Given function is
$f(x)=\sqrt { e ^{ \sqrt x }}$
Lets take $g(x ) = \sqrt x$
Now, our function reduces to
$f(x) = \sqrt {e^{g(x)}}$
Now,
$f^{'}(x) = g^{'}(x).\frac{1}{2\sqrt{e^{g(x)}}}.\frac{d({e^{g(x)}})}{dx} = g{'}(x).\frac{1}{2\sqrt{e^{g(x)}}}.{e^{g(x)}} = \frac{g^{'}(x).e^{g(x)}}{2.\sqrt{e^{g(x)}}} = \frac{g^{'}(x).e^{\sqrt x}}{2.\sqrt{e^{\sqrt x}}}$ -(i)
And
$g(x)=\sqrt x\\\Rightarrow g^{'}(x) = \frac{(\sqrt x)}{dx}=\frac{1}{2\sqrt x}$
Put this value in our equation (i)
$f^{'}(x) =\frac{e^{\sqrt x}}{2\sqrt x.2.\sqrt{e^{\sqrt x}}} = \frac{e^{\sqrt x}}{4\sqrt{xe^{\sqrt x}}}$
Therefore, the answer is $\frac{e^{\sqrt x}}{4\sqrt{xe^{\sqrt x}}}.\ \ x>0$

Question:8 Differentiate the following w.r.t. x: $\log ( \log x ) , x > 1$

Answer:

Given function is
$f(x)=\log ( \log x )$
Lets take $g(x ) = \log x$
Now, our function reduces to
$f(x) = \log(g(x))$
Now,
$f^{'}(x) = g^{'}(x).\frac{1}{g(x)}$ -(i)
And
$g(x)=\log x\\\Rightarrow g^{'}(x) = \frac{1}{x}$
Put this value in our equation (i)
$f^{'}(x) =\frac{1}{x}.\frac{1}{\log x} = \frac{1}{x\log x}$
Therefore, the answer is $\frac{1}{x\log x}, \ \ x>1$

Question:9. Differentiate the following w.r.t. x:

$\frac{\cos x }{\log x} , x > 0$

Answer:

Given function is
$f(x)=\frac{\cos x }{\log x}$
We differentiate with the help of Quotient rule
$f^{'}(x)=\frac{\frac{d(\cos x)}{dx}.\log x-\cos x.\frac{(\log x)}{dx} }{(\log x)^2 }$
$=\frac{(-\sin x).\log x-\cos x.\frac{1}{x} }{(\log x)^2 } = \frac{-(x\sin x\log x+\cos x)}{x(\log x)^2}$
Therefore, the answer is $\frac{-(x\sin x\log x+\cos x)}{x(\log x)^2}$

Question:10. Differentiate the following w.r.t. x:

$\cos ( log x + e ^x ) , x > 0$

Answer:

Given function is
$f(x)=\cos ( log x + e ^x )$
Lets take $g(x) = ( log x + e ^x )$
Then , our function reduces to
$f(x) = \cos (g(x))$
Now, differentiation w.r.t. x is
$f^{'}(x) = g^{'}(x)\(-\sin) (g(x))$ -(i)
And
$g(x) = ( log x + e ^x )$
$g^{'}(x)= \frac{d(\log x)}{dx}+\frac{d(e^x)}{dx} = \frac{1}{x}+e^x$
Put this value in our equation (i)
$f^{'}(x) = -\left ( \frac{1}{x}+e^x \right )\sin (\log x+e^x)$
Therefore, the answer is $-\left ( \frac{1}{x}+e^x \right )\sin (\log x+e^x), x>0$

Class 12 Maths Chapter 5 NCERT solutions: Exercise: 5.5

Question:1 Differentiate the functions w.r.t. x. $\cos x . \cos 2x .\cos 3x$

Answer:

Given function is
$y=\cos x . \cos 2x .\cos 3x$
Now, take log on both sides
$\log y=\log (\cos x . \cos 2x .\cos 3x)\\ \log y = \log \cos x + \log \cos 2x + \log \cos 3x$
Now, differentiation w.r.t. x
$\log y=\log (\cos x . \cos 2x .\cos 3x)\\ \frac{d(\log y )}{dx} = \frac{\log \cos x}{dx} + \frac{\log \cos 2x}{dx} + \frac{\log \cos 3x}{dx}\\ \frac{1}{y}.\frac{dy}{dx} = (-\sin x)\frac{1}{\cos x}+(-2\sin 2x)\frac{1}{\cos 2x}+(-3\sin3x).\frac{1}{\cos3x}\\ \frac{1}{y}\frac{dy}{dx} = -(\tan x+\tan 2x+\tan 3x) \ \ \ \ \ \ (\because \frac{\sin x }{\cos x} =\tan x)\\ \frac{dy}{dx}=-y(\tan x+\tan 2x+\tan 3x)\\ \frac{dy}{dx}= -\cos x\cos 2x\cos 3x(\tan x+\tan 2x+\tan 3x)$
There, the answer is $-\cos x\cos 2x\cos 3x(\tan x+\tan 2x+\tan 3x)$

Question:2. Differentiate the functions w.r.t. x.

$\sqrt {\frac{(x-1) ( x-2)}{(x-3 )(x-4 ) (x-5)}}$

Answer:

Given function is
$y=\sqrt {\frac{(x-1) ( x-2)}{(x-3 )(x-4 ) (x-5)}}$
Take log on both the sides
$\log y=\frac{1}{2}\log\left ( \frac{(x-1) ( x-2)}{(x-3 )(x-4 ) (x-5)} \right )\\ \log y = \frac{1}{2} (\log(x-1)+\log(x-2)-\log(x-3)-\log(x-4)-\log(x-5))\\$
Now, differentiation w.r.t. x is
$\frac{d(\log y)}{dx} = \frac{1}{2} (\frac{d(\log(x-1))}{dx}+\frac{d(\log(x-2))}{dx}-\frac{d(\log(x-3))}{dx}-\frac{d(\log(x-4))}{dx}-\\$ $\frac{d(\log(x-5))}{dx})$
$\frac{1}{y}\frac{dy}{dx}=\frac{1}{2}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5})\\ \frac{dy}{dx}=y\frac{1}{2}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5})\\ \frac{dy}{dx} = \frac{1}{2}\sqrt {\frac{(x-1) ( x-2)}{(x-3 )(x-4 ) (x-5)}}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5})$
Therefore, the answer is $\frac{1}{2}\sqrt {\frac{(x-1) ( x-2)}{(x-3 )(x-4 ) (x-5)}}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5})$

Question:3 Differentiate the functions w.r.t. x. $(\log x ) ^{\cos x}$

Answer:

Given function is
$y=(\log x ) ^{\cos x}$
take log on both the sides
$\log y=\cos x\log (\log x )$
Now, differentiation w.r.t x is
$\frac{d(\log y)}{dx} = \frac{d(\cos x\log(\log x))}{dx}\\ \frac{1}{y}.\frac{dy}{dx} = (-\sin x)(\log(\log x)) + \cos x.\frac{1}{\log x}.\frac{1}{x}\\ \frac{dy}{dx}= y( \cos x.\frac{1}{\log x}.\frac{1}{x}-\sin x\log(\log x) )\\ \frac{dy}{dx} = (\log x)^{\cos x}( \frac{\cos x}{x\log x}-\sin x\log(\log x) )$
Therefore, the answer is $(\log x)^{\cos x}( \frac{\cos x}{x\log x}-\sin x\log(\log x) )$

Question:4 Differentiate the functions w.r.t. x. $x ^x - 2 ^{ \sin x }$

Answer:

Given function is
$y = x ^x - 2 ^{ \sin x }$
Let's take $t = x^x$
take log on both the sides
$\log t=x\log x\\$
Now, differentiation w.r.t x is
$\log t=x\log x\\ \frac{d(\log t)}{dt}.\frac{dt}{dx} = \frac{d(x\log x)}{dx} \ \ \ \ \ \ \ (by \ chain \ rule)\\ \frac{1}{t}.\frac{dt}{dx} = \log x +1\\ \frac{dt}{dx} = t(\log x+1)\\ \frac{dt}{dx}= x^x(\log x+1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because t = x^x )$
Similarly, take $k = 2^{\sin x}$
Now, take log on both sides and differentiate w.r.t. x
$\log k=\sin x\log 2\\ \frac{d(\log k)}{dk}.\frac{dk}{dx} = \frac{d(\sin x\log 2)}{dx} \ \ \ \ \ \ \ (by \ chain \ rule)\\ \frac{1}{k}.\frac{dk}{dx} = \cos x \log 2\\ \frac{dk}{dx} = k(\cos x\log 2)\\ \frac{dk}{dx}= 2^{\sin x}(\cos x\log 2) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because k = 2^{\sin x} )$
Now,
$\frac{dy}{dx} = \frac{dt}{dx}-\frac{dk}{dx}\\ \frac{dy}{dx} = x^x(\log x+1 )- 2^{\sin x}(\cos x\log 2)$

Therefore, the answer is $x^x(\log x+1 )- 2^{\sin x}(\cos x\log 2)$

Question:5 Differentiate the functions w.r.t. x. $( x+3 )^ 2 . ( x +4 )^ 3 . ( x+5 )^4$

Answer:

Given function is
$y=( x+3 )^ 2 . ( x +4 )^ 3 . ( x+5 )^4$
Take log on both sides
$\log y=\log [( x+3 )^ 2 . ( x +4 )^ 3 . ( x+5 )^4]\\ \log y = 2\log(x+3)+3\log(x+4)+4\log(x+5)$
Now, differentiate w.r.t. x we get,
$\frac{1}{y}.\frac{dy}{dx} = 2.\frac{1}{x+3}+3.\frac{1}{x+4}+4.\frac{1}{x+5}\\ \frac{dy}{dx}=y\left ( \frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5} \right )\\ \frac{dy}{dx} = (x+3)^2.(x+4)^3.(x+5)^4.\left ( \frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5} \right )\\ \frac{dy}{dx} = (x+3)^2.(x+4)^3.(x+5)^4.\left ( \frac{2(x+4)(x+5)+3(x+3)(x+5)+4(x+3)(x+4)}{(x+3)(x+4)(x+5)} \right )\\ \frac{dy}{dx} = (x + 3) (x + 4)^2 (x + 5)^3 (9x^2 + 70x + 133)$
Therefore, the answer is $(x + 3) (x + 4)^2 (x + 5)^3 (9x^2 + 70x + 133)$

Question:6 Differentiate the functions w.r.t. x. $( x+ \frac{1}{x} ) ^ x + x ^{ 1 + \frac{1}{x} }$

Answer:

Given function is
$y = ( x+ \frac{1}{x} ) ^ x + x ^{ 1 + \frac{1}{x} }$
Let's take $t = ( x+ \frac{1}{x} ) ^ x$
Now, take log on both sides
$\log t =x \log ( x+ \frac{1}{x} )$
Now, differentiate w.r.t. x
we get,
$\frac{1}{t}.\frac{dt}{dx}=\log \left ( x+\frac{1}{x} \right )+x(1-\frac{1}{x^2}).\frac{1}{\left ( x+\frac{1}{x} \right )} = \frac{x^2-1}{x^2+1}+\log \left ( x+\frac{1}{x} \right )\\ \frac{dt}{dx} = t(\left (\frac{x^2-1}{x^2+1} \right )+\log \left ( x+\frac{1}{x} \right ))\\ \frac{dt}{dx} = \left ( x+\frac{1}{x} \right )^x (\left (\frac{x^2-1}{x^2+1} \right )+\log \left ( x+\frac{1}{x} \right ))$
Similarly, take $k = x^{1+\frac{1}{x}}$
Now, take log on both sides
$\log k = ({1+\frac{1}{x}})\log x$
Now, differentiate w.r.t. x
We get,
$\frac{1}{k}.\frac{dk}{dx}=\frac{1}{x} \left ( 1+\frac{1}{x} \right )+(-\frac{1}{x^2}).\log x = \frac{x^2+1}{x^2}+\frac{-1}{x^2}.\log x\\ \frac{dk}{dx} = t(\frac{x^2+1}{x^2}+\left (\frac{-1}{x^2} \right )\log x)\\ \frac{dk}{dx} = x^{x+\frac{1}{x}}\left (\frac{x^2+1-\log x}{x^2} \right )$
Now,
$\frac{dy}{dx} = \frac{dt}{dx}+\frac{dk}{dx}$
$\frac{dy}{dx} = \left ( x+\frac{1}{x} \right )^x (\left (\frac{x^2-1}{x^2+1} \right )+\log \left ( x+\frac{1}{x} \right ))+x^{x+\frac{1}{x}}\left (\frac{x^2+1-\log x}{x^2} \right )$

Therefore, the answer is $\left ( x+\frac{1}{x} \right )^x (\left (\frac{x^2-1}{x^2+1} \right )+\log \left ( x+\frac{1}{x} \right ))+x^{x+\frac{1}{x}}\left (\frac{x^2+1-\log x}{x^2} \right )$

Question:7 Differentiate the functions w.r.t. x. $(\log x )^x + x ^{\log x }$

Answer:

Given function is
$y = (\log x )^x + x ^{\log x }$
Let's take $t = (\log x)^x$
Now, take log on both the sides
$\log t = x \log(\log x)$
Now, differentiate w.r.t. x
we get,
$\frac{1}{t}\frac{dt}{dx} = \log (\log x) + x.\frac{1}{x}.\frac{1}{\log x}= \log (\log x)+\frac{1}{\log x}\\ \frac{dt}{dx}= t.(\log (\log x)+\frac{1}{\log x})\\ \frac{dt}{dx} =(\log x)^x(\log (\log x)) + (\log x)^x.\frac{1}{\log x}=(\log x)^x(\log (\log x))+ (\log x )^{x-1}$
Similarly, take $k = x^{\log x}$
Now, take log on both sides
$\log k = \log x \log x = (\log x)^2$
Now, differentiate w.r.t. x
We get,
$\frac{1}{k}\frac{dk}{dx} =2 (\log x).\frac{1}{x} \\ \frac{dt}{dx}= k.\left ( 2 (\log x).\frac{1}{x} \right )\\ \frac{dt}{dx} = x^{\log x}.\left (2 (\log x).\frac{1}{x} \right ) = 2x^{\log x-1}.\log x$
Now,
$\frac{dy}{dx} = \frac{dt}{dx}+\frac{dk}{dx}$
$\frac{dy}{dx} =(\log x)^x(\log (\log x))+ (\log x )^{x-1}+ 2x^{\log x-1}.\log x$
Therefore, the answer is $(\log x)^x(\log (\log x))+ (\log x )^{x-1}+ 2x^{\log x-1}.\log x$

Question:8 Differentiate the functions w.r.t. x. $(\sin x )^x + \sin ^{-1} \sqrt x$

Answer:

Given function is
$(\sin x )^x + \sin ^{-1} \sqrt x$
Lets take $t = (\sin x)^x$
Now, take log on both the sides
$\log t = x \log(\sin x)$
Now, differentiate w.r.t. x
we get,
$\frac{1}{t}\frac{dt}{dx} = \log (\sin x) + x.\cos x.\frac{1}{\sin x}= \log (\sin x)+x.\cot x \ \ \ (\because \frac{\cos x}{\sin x}=\cot x)\\ \frac{dt}{dx}= t.(\log (\sin x)+x.\cot x)\\ \frac{dt}{dx} =(\sin x)^x(\log (\sin x)+x\cot x)$
Similarly, take $k = \sin^{-1}\sqrt x$
Now, differentiate w.r.t. x
We get,
$\frac{dk}{dt} = \frac{1}{\sqrt{1-(\sqrt x)^2}}.\frac{1}{2\sqrt x}= \frac{1}{2\sqrt{x-x^2}}\\ \frac{dk}{dt}=\frac{1}{2\sqrt{x-x^2}}\\$
Now,
$\frac{dy}{dx} = \frac{dt}{dx}+\frac{dk}{dx}$
$\frac{dy}{dx} =(\sin x)^x(\log (\sin x)+x\cot x)+\frac{1}{2\sqrt{x-x^2}}$
Therefore, the answer is $(\sin x)^x(\log (\sin x)+x\cot x)+\frac{1}{2\sqrt{x-x^2}}$

Question:9 Differentiate the functions w.r.t. x 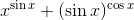$x ^ { \sin x } + ( \sin x )^ \cos x$

Answer:

Given function is
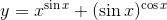
$y = x ^ { \sin x } + ( \sin x )^ \cos x$

Now, take $t = x^{\sin x}$
Now, take log on both sides
$\log t = \sin x \log x$
Now, differentiate it w.r.t. x
we get,
$\frac{1}{t}\frac{dt}{dx} = \cos x \log x+\frac{1}{x}.\sin x\\ \frac{dt}{dx}=t\left ( \cos x \log x+\frac{1}{x}.\sin x \right )\\ \frac{dt}{dx}= x^{\sin x}\left ( \cos x \log x+\frac{1}{x}.\sin x \right )$
Similarly, take $k = (\sin x)^{\cos x}$
Now, take log on both the sides
$\log k = \cos x \log (\sin x)$
Now, differentiate it w.r.t. x
we get,
$\frac{1}{k}\frac{dk}{dt} = (-\sin x)(\log (\sin x)) + \cos x.\frac{1}{\sin x}.\cos x=-\sin x\log(\sin x)+\cot x.\cos x\\ \frac{dk}{dt}= k\left ( -\sin x\log(\sin x)+\cot x.\cos x \right )\\ \frac{dk}{dt}=(\sin x)^{\cos x}\left ( -\sin x\log(\sin x)+\cot x.\cos x \right )$
Now,
$\frac{dy}{dx} = x^{\sin x}\left ( \cos x \log x+\frac{1}{x}.\sin x \right )+ (\sin x)^{\cos x}\left ( -\sin x\log(\sin x)+\cot x.\cos x \right )$
Therefore, the answer is $x^{\sin x}\left ( \cos x \log x+\frac{1}{x}.\sin x \right )+ (\sin x)^{\cos x}\left ( -\sin x\log(\sin x)+\cot x.\cos x \right )$

Question:10 Differentiate the functions w.r.t. x. $x ^ {x \cos x} + \frac{x^2 + 1 }{x^2 -1 }$

Answer:

Given function is
$x ^ {x \cos x} + \frac{x^2 + 1 }{x^2 -1 }$
Take $t = x^{x\cos x}$
Take log on both the sides
$\log t =x\cos x \log x$
Now, differentiate w.r.t. x
we get,
$\frac{1}{t}\frac{dt}{dx} = \cos x\log x-x\sin x\log x + \frac{1}{x}.x.\cos x\\ \frac{dt}{dx}= t.\left (\log x(\cos x-x\sin x)+ \cos x \right ) = x^{x\cos x}\left ( \log x(\cos x-x\sin x)+ \cos x \right )$
Similarly,
take $k = \frac{x^2+1}{x^2-1}$
Now. differentiate it w.r.t. x
we get,
$\frac{dk}{dx} = \frac{2x(x^2-1)-2x(x^2+1)}{(x^2-1)^2} = \frac{2x^3-2x-2x^3-2x}{(x^2-1)^2} = \frac{-4x}{(x^2-1)^2}$
Now,
$\frac{dy}{dx} = \frac{dt}{dx}+\frac{dk}{dx}$
$\frac{dy}{dx} = x^{x\cos x}\left ( \log x(\cos x-x\sin x)+ \cos x \right )-\frac{4x}{(x^2-1)^2}$
Therefore, the answer is $x^{x\cos x}\left ( \cos x(\log x+1)-x\sin x\log x\right )-\frac{4x}{(x^2-1)^2}$

Question:11 Differentiate the functions w.r.t. x. $( x \cos x )^ x + ( x \sin x )^{1/ x}$

Answer:

Given function is
$f(x)=( x \cos x )^ x + ( x \sin x )^{1/ x}$
Let's take $t = (x\cos x)^x$
Now, take log on both sides
$\log t =x\log (x\cos x) = x(\log x+\log \cos x)$
Now, differentiate w.r.t. x
we get,
$\frac{1}{t}\frac{dt}{dx} =(\log x+\log \cos x)+x(\frac{1}{x}+\frac{1}{\cos x}.(-\sin x))\\ \frac{dt}{dx} = t(\log x + \log \cos x+1-x\tan x) \ \ \ \ \ \ \ \ \ (\because \frac{\sin x}{\cos x}= \tan x)\\ \frac{dt}{dx}= (x\cos x)^x(\log x + \log \cos x+1-x\tan x)\\ \frac{dt}{dx}=(x\cos x)^x(+1-x\tan x+\log (x\cos x))$
Similarly, take $k = (x\sin x)^{\frac{1}{x}}$
Now, take log on both the sides
$\log k = \frac{1}{x}(\log x+\log \sin x)$
Now, differentiate w.r.t. x
we get,
$\frac{1}{k}\frac{dk}{dx} =(\frac{-1}{x^2})(\log x+\log \sin x)+\frac{1}{x}(\frac{1}{x}+\frac{1}{\sin x}.(\cos x))\\ \frac{dk}{dx} = \frac{k}{x^2}(-\log x - \log \sin x+\frac{1}{x^2}+\frac{\cot x}{x}) \ \ \ \ \ \ \ \ \ (\because \frac{\cos x}{\sin x}= \cot x)\\ \frac{dk}{dx}=\frac{(x\sin x)^{\frac{1}{x}}}{x^2}(-\log x - \log \sin x+\frac{1}{x^2}+\frac{\cot x}{x})\\ \frac{dk}{dx}=(x\sin x)^{\frac{1}{x}}\frac{(x\cot x+1-(\log x\sin x))}{x^2}$
Now,
$\frac{dy}{dx}= \frac{dt}{dx}+\frac{dk}{dx}$
$\frac{dy}{dx}= (x\cos x)^x(+1-x\tan x+\log (x\cos x))+(x\sin x)^{\frac{1}{x}}\frac{(x\cot x+1-(\log x\sin x))}{x^2}$
Therefore, the answer is $(x\cos x)^x(1-x\tan x+\log (x\cos x))+(x\sin x)^{\frac{1}{x}}\frac{(x\cot x+1-(\log x\sin x))}{x^2}$

Question:12 Find dy/dx of the functions given in Exercises 12 to 15

$x ^ y + y ^ x = 1$ .

Answer:

Given function is
$f(x)=x ^ y + y ^ x = 1$
Now, take $t = x^y$
take log on both sides
$\log t = y\log x$
Now, differentiate w.r.t x
we get,
$\frac{1}{t}\frac{dt}{dx} = \frac{dy}{dx}(\log x)+y\frac{1}{x}=\frac{dy}{dx}(\log x)+\frac{y}{x}\\ \frac{dt}{dx}= t(\frac{dy}{dx}(\log x)+\frac{y}{x})\\ \frac{dt}{dx}= ( x^y)(\frac{dy}{dx}(\log x)+\frac{y}{x})$
Similarly, take $k = y^x$
Now, take log on both sides
$\log k = x\log y$
Now, differentiate w.r.t. x
we get,
$\frac{1}{k}\frac{dk}{dx} = (\log y)+x\frac{1}{y}\frac{dy}{dx}=\log y+\frac{x}{y}\frac{dy}{dx}\\ \frac{dk}{dx}= k(\log y+\frac{x}{y}\frac{dy}{dx})\\ \frac{dk}{dx}= (y^x)(\log y+\frac{x}{y}\frac{dy}{dx})$
Now,
$f^{'}(x)= \frac{dt}{dx}+\frac{dk}{dx}= 0$

$( x^y)(\frac{dy}{dx}(\log x)+\frac{y}{x}) + (y^x)(\log y+\frac{x}{y}\frac{dy}{dx}) = 0\\ \frac{dy}{dx}(x^y(\log x)+xy^{x-1}) = -(yx^{y-1}+y^x(\log y))\\ \frac{dy}{dx}= \frac{ -(yx^{y-1}+y^x(\log y))}{(x^y(\log x)+xy^{x-1})}$

Therefore, the answer is $\frac{ -(yx^{y-1}+y^x(\log y))}{(x^y(\log x)+xy^{x-1})}$

Question:13 Find dy/dx of the functions given in Exercises 12 to 15.

$y^x = x ^y$

Answer:

Given function is
$f(x)\Rightarrow x ^ y = y ^ x$
Now, take $t = x^y$
take log on both sides
$\log t = y\log x$
Now, differentiate w.r.t x
we get,
$\frac{1}{t}\frac{dt}{dx} = \frac{dy}{dx}(\log x)+y\frac{1}{x}=\frac{dy}{dx}(\log x)+\frac{y}{x}\\ \frac{dt}{dx}= t(\frac{dy}{dx}(\log x)+\frac{y}{x})\\ \frac{dt}{dx}= ( x^y)(\frac{dy}{dx}(\log x)+\frac{y}{x})$
Similarly, take $k = y^x$
Now, take log on both sides
$\log k = x\log y$
Now, differentiate w.r.t. x
we get,
$\frac{1}{k}\frac{dk}{dx} = (\log y)+x\frac{1}{y}\frac{dy}{dx}=\log y+\frac{x}{y}\frac{dy}{dx}\\ \frac{dk}{dx}= k(\log y+\frac{x}{y}\frac{dy}{dx})\\ \frac{dk}{dx}= (y^x)(\log y+\frac{x}{y}\frac{dy}{dx})$
Now,
$f^{'}(x)\Rightarrow \frac{dt}{dx}= \frac{dk}{dx}$

$( x^y)(\frac{dy}{dx}(\log x)+\frac{y}{x}) = (y^x)(\log y+\frac{x}{y}\frac{dy}{dx})\\ \frac{dy}{dx}(x^y(\log x)-xy^{x-1}) = (y^x(\log y)-yx^{y-1})\\ \frac{dy}{dx}= \frac{ y^x(\log y)-yx^{y-1}}{(x^y(\log x)-xy^{x-1})} = \frac{x}{y}\left ( \frac{y-x\log y}{x-y\log x}\right )$

Therefore, the answer is $\frac{x}{y}\left ( \frac{y-x\log y}{x-y\log x}\right )$

Question:14 Find dy/dx of the functions given in Exercises 12 to 15. $( \cos x )^y = ( \cos y )^x$

Answer:

Given function is
$f(x)\Rightarrow (\cos x) ^ y = (\cos y) ^ x$
Now, take log on both the sides
$y\log \cos x = x \log \cos y$
Now, differentiate w.r.t x
$\frac{dy}{dx}(\log \cos x)-y\tan x = \log \cos y-x\tan y\frac{dy}{dx}$
By taking similar terms on the same side
We get,
$(\frac{dy}{dx}(\log \cos x)-y\tan x) = (\log \cos y-x\tan y\frac{dy}{dx})\\ \frac{dy}{dx} \left (\log \cos x+(\cos y)^x.x\tan y) \right )= \left ( \log \cos y+(\cos x)^y.y\tan x \right )\\ \frac{dy}{dx}= \frac{\left (\log \cos y+y\tan x \right )}{\left ( \log \cos x+x\tan y) \right )} = \frac{y\tan x+\log \cos y}{x\tan y+\log \cos x}$

Therefore, the answer is $\frac{y\tan x+\log \cos y}{x\tan y+\log \cos x}$

Question:15 Find dy/dx of the functions given in Exercises 12 to 15. $xy = e ^{x-y}$

Answer:

Given function is
$f(x)\Rightarrow xy = e ^{x-y}$
Now, take take log on both the sides
$\log x+\ log y = (x-y)(1) \ \ \ \ \ \ \ \ \ \ \ \ (\because \log e = 1)\\ \log x+\ log y = (x-y)$
Now, differentiate w.r.t x
$\frac{1}{x}+\frac{1}{y}\frac{dy}{dx}=1-\frac{dy}{dx}$
By taking similar terms on same side
We get,
$(\frac{1}{y}+1)\frac{dy}{dx}=1-\frac{1}{x}\\ \frac{y+1}{y}.\frac{dy}{dx}= \frac{x-1}{x}\\ \frac{dy}{dx}= \frac{y}{x}.\frac{x-1}{y+1}$
Therefore, the answer is $\frac{y}{x}.\frac{x-1}{y+1}$

Question:16 Find the derivative of the function given by $f (x) = (1 + x) (1 + x^2) (1 + x^4) (1 + x^8)$ and hence find

f ' (1)

Answer:

Given function is
$y = (1 + x) (1 + x^2) (1 + x^4) (1 + x^8)$
Take log on both sides
$\log y =\log (1 + x) + \log (1 + x^2) +\log (1 + x^4) +\log (1 + x^8)$
NOW, differentiate w.r.t. x
$\frac{1}{y}.\frac{dy}{dx} = \frac{1}{1+x}+ \frac{2x}{1+x^2}+ \frac{4x^3}{1+x^4}+ \frac{8x^7}{1+x^8}\\ \frac{dy}{dx}=y.\left ( \frac{1}{1+x}+ \frac{2x}{1+x^2}+ \frac{4x^3}{1+x^4}+ \frac{8x^7}{1+x^8} \right )\\ \frac{dy}{dx}= (1 + x) (1 + x^2) (1 + x^4) (1 + x^8).\left ( \frac{1}{1+x}+ \frac{2x}{1+x^2}+ \frac{4x^3}{1+x^4}+ \frac{8x^7}{1+x^8} \right )$
Therefore, $f^{'}(x)= (1 + x) (1 + x^2) (1 + x^4) (1 + x^8).\left ( \frac{1}{1+x}+ \frac{2x}{1+x^2}+ \frac{4x^3}{1+x^4}+ \frac{8x^7}{1+x^8} \right )$
Now, the vale of $f^{'}(1)$ is
$f^{'}(1)= (1 + 1) (1 + 1^2) (1 + 1^4) (1 + 1^8).\left ( \frac{1}{1+1}+ \frac{2(1)}{1+1^2}+ \frac{4(1)^3}{1+1^4}+ \frac{8(1)^7}{1+1^8} \right )\\ f^{'}(1)=16.\frac{15}{2} = 120$

Question:17 (1) Differentiate $(x^2 - 5x + 8) (x^3 + 7x + 9)$ in three ways mentioned below:
(i) by using product rule

Answer:

Given function is
$f(x)=(x^2 - 5x + 8) (x^3 + 7x + 9)$
Now, we need to differentiate using the product rule
$f^{'}(x)=\frac{d((x^2 - 5x + 8))}{dx}. (x^3 + 7x + 9)+(x^2 - 5x + 8).\frac{d( (x^3 + 7x + 9))}{dx}\\$
$= (2x-5).(x^3+7x+9)+(x^2-5x+8)(3x^2+7)\\ =2x^4+14x^2+18x-5x^3-35x-45+3x^4-15x^3+24x^2+7x^2-35x+56\\ = 5x^4 -20x^3+45x^2-52x+11$
Therefore, the answer is $5x^4 -20x^3+45x^2-52x+11$

Question:17 (2) Differentiate $(x^2 - 5x + 8) (x^3 + 7x + 9)$ in three ways mentioned below:
(ii) by expanding the product to obtain a single polynomial.

Answer:

Given function is
$f(x)=(x^2 - 5x + 8) (x^3 + 7x + 9)$
Multiply both to obtain a single higher degree polynomial
$f(x) = x^2(x^3+7x+9)-5x(x^3+7x+9)+8(x^3+7x+9)$
$= x^5+7x^3+9x^2-5x^4-35x^2-45x+8x^3+56x+72$
$= x^5-5x^4+15x^3-26x^2+11x+72$
Now, differentiate w.r.t. x
we get,
$f^{'}(x)=5x^4-20x^3+45x^2-52x+11$
Therefore, the answer is $5x^4-20x^3+45x^2-52x+11$

Question:17 (3) Differentiate $(x^2 - 5x + 8) (x^3 + 7x + 9)$ in three ways mentioned below:
(iii) by logarithmic differentiation.
Do they all give the same answer?

Answer:

Given function is
$y=(x^2 - 5x + 8) (x^3 + 7x + 9)$
Now, take log on both the sides
$\log y = \log (x^2-5x+8)+\log (x^3+7x+9)$
Now, differentiate w.r.t. x
we get,
$\frac{1}{y}.\frac{dy}{dx} = \frac{1}{x^2-5x+8}.(2x-5) + \frac{1}{x^3+7x+9}.(3x^2+7)\\ \frac{dy}{dx}= y.\left ( \frac{(2x-5)(x^3+7x+9)+(3x^2+7)(x^2-5x+8)}{(x^2-5x+8)(x^3+7x+9)} \right )\\ \frac{dy}{dx}=(x^2-5x+8)(x^3+7x+9).\left ( \frac{(2x-5)(x^3+7x+9)+(3x^2+7)(x^2-5x+8)}{(x^2-5x+8)(x^3+7x+9)} \right )\\ \frac{dy}{dx} = (2x-5)(x^3+7x+9)+(3x^2+7)(x^2-5x+8)\\ \frac{dy}{dx} = 5x^4-20x^3+45x^2-56x+11$
Therefore, the answer is $5x^4-20x^3+45x^2-56x+11$
And yes they all give the same answer

Question:18 If u, v and w are functions of x, then show that $\frac{d}{dx} ( u,v,w) = \frac{du}{dx} v. w +u . \frac{dv }{dx } v. w+ u . \frac{dv}{dx } . w+u.v \frac{dw}{dx}$ in two ways - first by repeated application of product rule, second by logarithmic differentiation.

Answer:

It is given that u, v and w are the functions of x
Let $y = u.v.w$
Now, we differentiate using product rule w.r.t x
First, take $y = u.(vw)$
Now,
$\frac{dy}{dx}= \frac{du}{dx}.(v.w) + \frac{d(v.w)}{dx}.u$ -(i)
Now, again by the product rule
$\frac{d(v.w)}{dx}= \frac{dv}{dx}.w + \frac{dw}{dx}.v$
Put this in equation (i)
we get,
$\frac{dy}{dx}= \frac{du}{dx}.(v.w) + \frac{dv}{dx}.(u.w) + \frac{dw}{dx}.(u.v)$
Hence, by product rule we proved it

Now, by taking the log
Again take $y = u.v.w$
Now, take log on both sides
$\log y = \log u + \log v + \log w$
Now, differentiate w.r.t. x
we get,
$\frac{1}{y}.\frac{dy}{dx} = \frac{1}{u}.\frac{du}{dx}+\frac{1}{v}\frac{dv}{dx}+\frac{1}{w}.\frac{dw}{dx}\\ \frac{dy}{dx}= y. \left ( \frac{v.w.\frac{du}{dx}+u.w.\frac{dv}{dx}+u.v.\frac{dw}{dx}}{u.v.w} \right )\\ \frac{dy}{dx} = (u.v.w)\left ( \frac{v.w.\frac{du}{dx}+u.w.\frac{dv}{dx}+u.v.\frac{dw}{dx}}{u.v.w} \right )\\$
$\frac{dy}{dx}= \frac{du}{dx}.(v.w) + \frac{dv}{dx}.(u.w) + \frac{dw}{dx}.(u.v)$
Hence, we proved it by taking the log

Class 12 Maths Chapter 5 NCERT solutions: Exercise:5.6

Question:1 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx .

$x = 2at^2, y = at^4$

Answer:

Given equations are
$x = 2at^2, y = at^4$
Now, differentiate both w.r.t t
We get,
$\frac{dx}{dt}=\frac{d(2at^2)}{dt}= 4at$
Similarly,
$\frac{dy}{dt}=\frac{d(at^4)}{dt}= 4at^3$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{4at^3}{4at} = t^2$
Therefore, the answer is $\frac{dy}{dx}= t^2$

Question:2 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx .

$x= a \cos \theta , y = b \cos \theta$

Answer:

Given equations are
$x= a \cos \theta , y = b \cos \theta$
Now, differentiate both w.r.t $\theta$
We get,
$\frac{dx}{d\theta}=\frac{d(a\cos \theta)}{d\theta}= -a\sin \theta$
Similarly,
$\frac{dy}{d\theta}=\frac{d(b\cos \theta)}{d\theta}= -b\sin \theta$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}= \frac{-b\sin \theta}{-a\sin \theta} = \frac{b}{a}$
Therefore, answer is $\frac{dy}{dx}= \frac{b}{a}$

Question:3 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx . $x = \sin t , y = \cos 2 t$

Answer:

Given equations are
$x = \sin t , y = \cos 2 t$
Now, differentiate both w.r.t t
We get,
$\frac{dx}{dt}=\frac{d(\sin t)}{dt}= \cos t$
Similarly,
$\frac{dy}{dt}=\frac{d(\cos 2t)}{dt}= -2\sin 2t = -4\sin t \cos t \ \ \ \ \ (\because \sin 2x = \sin x\cos x)$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{-4\sin t \cos t }{\cos t} = -4\sin t$
Therefore, the answer is $\frac{dy}{dx} = -4\sin t$

Question:4 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx

$x = 4t , y = 4/t$

Answer:

Given equations are
$x = 4t , y = 4/t$
Now, differentiate both w.r.t t
We get,
$\frac{dx}{dt}=\frac{d(4 t)}{dt}= 4$
Similarly,
$\frac{dy}{dt}=\frac{d(\frac{4}{t})}{dt}= \frac{-4}{t^2}$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{ \frac{-4}{t^2} }{4} = \frac{-1}{t^2}$
Therefore, the answer is $\frac{dy}{dx} = \frac{-1}{t^2}$

Question:5 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = \cos \theta - \cos 2\theta , y = \sin \theta - \sin 2 \theta$

Answer:

Given equations are
$x = \cos \theta - \cos 2\theta , y = \sin \theta - \sin 2 \theta$
Now, differentiate both w.r.t $\theta$
We get,
$\frac{dx}{d\theta}=\frac{d(\cos \theta-\cos 2\theta)}{d\theta}= -\sin \theta -(-2\sin 2\theta) = 2\sin 2\theta - \sin \theta$
Similarly,
$\frac{dy}{d\theta}=\frac{d(\sin \theta - \sin 2\theta)}{d\theta}= \cos \theta -2\cos2 \theta$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}= \frac{\cos \theta -2\cos 2 \theta}{2\sin2\theta-\sin \theta}$
Therefore, answer is $\frac{dy}{dx}= \frac{\cos \theta -2\cos 2 \theta}{2\sin2\theta-\sin \theta}$

Question:6 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = a ( \theta - \sin \theta ) , y = a ( 1+ \cos \theta )$

Answer:

Given equations are
$x = a ( \theta - \sin \theta ) , y = a ( 1+ \cos \theta )$
Now, differentiate both w.r.t $\theta$
We get,
$\frac{dx}{d\theta}=\frac{d(a(\theta- \sin \theta))}{d\theta}= a(1-\cos \theta)$
Similarly,
$\frac{dy}{d\theta}=\frac{d(a(1+\cos \theta))}{d\theta}=-a\sin \theta$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}= \frac{-a\sin \theta}{a(1-\cos \theta)} = \frac{-\sin }{1-\cos \theta} =- \cot \frac{\theta}{2} \ \ \ \ \ \ \ (\cot \frac{x}{2}=\frac{\sin x}{1-\cos x})$
Therefore, the answer is $\frac{dy}{dx}=-\cot \frac{\theta}{2}$

Question:7 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = \frac{\sin ^3 t }{\sqrt {\cos 2t }} , y = \frac{\cos ^3 t }{\sqrt {\cos 2t }}$

Answer:

Given equations are
$x = \frac{\sin ^3 t }{\sqrt {\cos 2t }} , y = \frac{\cos ^3 t }{\sqrt {\cos 2t }}$
Now, differentiate both w.r.t t
We get,
$\frac{dx}{dt}=\frac{d(\frac{\sin ^3 t }{\sqrt {\cos 2t }})}{dt}=\frac{\sqrt{\cos 2t}.\frac{d(\sin^3t)}{dt}-\sin^3t.\frac{d(\sqrt{\cos2t})}{dt}}{(\sqrt{\cos2t})^2} =\frac{3\sin^2 t\cos t.\sqrt{\cos 2t}-\sin^3t.\frac{1}{2\sqrt{\cos 2t}}.(-2\sin 2t)}{{\cos 2t}}$
$=\frac{3\sin^2t\cos t . \cos 2t+sin^3t\sin 2t}{\cos2t\sqrt{\cos2t}}$
$=\frac{\sin^3t\sin2t(3\cot t \cot 2t+1)}{\cos2t\sqrt{\cos2t}} \ \ \ \ \ (\because \frac{\cos x}{\sin x}=\cot x)$
Similarly,
$\frac{dy}{dt}=\frac{d( \frac{\cos ^3 t }{\sqrt {\cos 2t }})}{dt}=\frac{\sqrt{\cos 2t}.\frac{d(\cos^3t)}{dt}-\cos^3t.\frac{d(\sqrt{\cos2t})}{dt}}{(\sqrt{\cos2t})^2} =\frac{3\cos^2 t(-\sin t).\sqrt{\cos 2t}-\cos^3t.\frac{1}{2\sqrt{\cos 2t}}.(-2\sin 2t)}{(\sqrt{\cos 2t})^2}$
$=\frac{-3\cos^2t\sin t\cos2t+\cos^3t\sin 2t}{\cos2t\sqrt{\cos2t}}$
$=\frac{ \sin2t\cos^3t(1-3\tan t \cot 2t)}{\cos2t\sqrt{\cos2t}}$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{\frac{ \sin2t\cos^3t(1-3\tan t \cot 2t)}{\cos2t\sqrt{\cos2t}} }{\frac{\sin^3t\sin2t(3\cot t \cot 2t+1)}{\cos2t\sqrt{\cos2t}}} = \frac{\cot^3t(1-3\tan t \cot 2t)}{(3\cot t \cot 2t+1)}$
$= \frac{\cos^3t(1-3.\frac{\sin t}{\cos t}.\frac{\cos2t}{\sin 2t})}{\sin^3t(3.\frac{\cos t}{\sin t}.\frac{\cos 2t}{\sin 2t}+1)} = \frac{\cos^2t(\cos t\sin2t -3\sin t \cos 2t)}{\sin^2t(3\cos t \cos2t+\sin t \sin 2t)}$
$=\frac{\cos^2t(\cos t .2\sin t \cos t - 3\sin t (2\cos^2t-1))}{\sin^2t(3\cos t(1-2\sin^2 2t)+\sin t.2\sin t \cos t)}$
$(\because \sin 2x = 2\sin x\cos x \ and \ \cos 2x = 2\cos^2x-1 \ and \ \cos 2x = 1-2\sin^2x)$
$=\frac{\cos^2t(2\sin t\cos^2 t-6\sin t\cos^2t+3\sin t)}{\sin^2t(3\cos t-6\cos t \sin^2t+2\sin^2\cos t)}\\=\frac{sint cost(-4cos^3t+3cost)}{sintcost(3sint-4sin^3t)}$

$\frac{dy}{dx} = \frac{-4\cos^3t+3\cos t}{3\sin t -4\sin^3 t}= \frac{-\cos 3t}{\sin 3t} = -\cot 3t$ $\left ( \because \sin3t = 3\sin t-4\sin^3t \\ \ and \ \cos3t = 4\cos^3t - 3\cos t \right )$

Therefore, the answer is $\frac{dy}{dx} = -\cot 3t$

Question:8 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = a ( \cos t + \log \tan t/2 ),y = a \sin t$

Answer:

Given equations are
$x = a ( \cos t + \log \tan \frac{t}{2} ),y = a \sin t$
Now, differentiate both w.r.t t
We get,
$\frac{dx}{dt}=\frac{d(a ( \cos t + \log \tan \frac{t}{2} ))}{dt}= a(-\sin t + \frac{1}{\tan\frac{t}{2}}.\sec^2\frac{t}{2}.\frac{1}{2})$
$= a(-\sin t+\frac{1}{2}.\frac{\cos \frac{t}{2}}{\sin\frac{t}{2}}.\frac{1}{\cos^2\frac{t}{2}}) = a(-\sin t+\frac{1}{2\sin \frac{t}{2}\cos \frac{t}{2}})$
$=a(-\sin t+\frac{1}{\sin 2.\frac{t}{2}} ) = a(\frac{-\sin^2t+1}{\sin t})= a(\frac{\cos^2t}{\sin t})$
Similarly,
$\frac{dy}{dt}=\frac{d(a\sin t)}{dt}= a\cos t$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{a \cos t }{ a(\frac{\cos^2t}{\sin t})} = \frac{\sin t}{\cos t} = \tan t$
Therefore, the answer is $\frac{dy}{dx} = \tan t$

Question:9 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = a \sec \theta , y = b \ tan \theta$

Answer:

Given equations are
$x = a \sec \theta , y = b \ tan \theta$
Now, differentiate both w.r.t $\theta$
We get,
$\frac{dx}{d\theta}=\frac{d(a\sec \theta)}{d\theta}= a\sec \theta \tan \theta$
Similarly,
$\frac{dy}{d\theta}=\frac{d(b\tan \theta)}{d\theta}= b\sec^2 \theta$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}= \frac{b\sec^2 \theta}{a\sec\theta\tan \theta} = \frac{b\sec\theta}{a\tan \theta}= \frac{b\frac{1}{\cos\theta}}{a\frac{\sin \theta}{\cos \theta}} = \frac{b }{a\sin \theta} = \frac{b cosec \theta}{a}$
Therefore, the answer is $\frac{dy}{dx} = \frac{b cosec \theta}{a}$

Question:10 If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dy/dx $x = a ( \cos \theta + \theta \sin \theta ) , y = a ( \sin \theta - \theta \cos \theta )$

Answer:

Given equations are
$x = a ( \cos \theta + \theta \sin \theta ) , y = a ( \sin \theta - \theta \cos \theta )$
Now, differentiate both w.r.t $\theta$
We get,
$\frac{dx}{d\theta}=\frac{d(a(\cos \theta+ \theta\sin \theta))}{d\theta}= a(-\sin \theta+\sin \theta+ \theta\cos \theta)= a \theta\cos \theta$
Similarly,
$\frac{dy}{d\theta}=\frac{d(a(\sin \theta- \theta\cos \theta))}{d\theta}= a(\cos \theta-\cos \theta+ \theta\sin \theta) = a \theta\sin \theta$
Now, $\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}= \frac{a \theta\sin \theta}{a \theta\cos \theta} = \tan \theta$
Therefore, the answer is $\frac{dy}{dx}= \tan \theta$

Question:11 If $x = \sqrt {a ^{\sin ^{-1}t}} , y = \sqrt { a ^{ \cos ^{-1}t}}$ , show that $dy/dx = - y /x$

Answer:

Given equations are
$x = \sqrt {a ^{\sin ^{-1}t}} , y = \sqrt { a ^{ \cos ^{-1}t}}$

$xy=\sqrt{a^{sin^{-1}t+cos^{-1}t}}\\since\ sin^{-1}x+cos^{-1}x=\frac{\pi}{2}\\xy=a^{\frac{\pi}{2}}=constant=c$

differentiating with respect to x

$x\frac{dy}{dx}+y=0\\\frac{dy}{dx}=\frac{-y}{x}$

Class 12 Maths Chapter 5 NCERT solutions: Exercise: 5.7

Question:1 Find the second order derivatives of the functions given in Exercises 1 to 10.

$x^2 + 3x+ 2$

Answer:

Given function is
$y=x^2 + 3x+ 2$
Now, differentiation w.r.t. x
$\frac{dy}{dx}= 2x+3$
Now, second order derivative
$\frac{d^2y}{dx^2}= 2$
Therefore, the second order derivative is $\frac{d^2y}{dx^2}= 2$

Question:2 Find the second order derivatives of the functions given in Exercises 1 to 10.

$x ^{20}$

Answer:

Given function is
$y=x ^{20}$
Now, differentiation w.r.t. x
$\frac{dy}{dx}= 20x^{19}$
Now, the second-order derivative is
$\frac{d^2y}{dx^2}= 20.19x^{18}= 380x^{18}$
Therefore, second-order derivative is $\frac{d^2y}{dx^2}= 380x^{18}$

Question:3 Find the second order derivatives of the functions given in Exercises 1 to 10.

$x \cos x$

Answer:

Given function is
$y = x \cos x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}= \cos x + x(-\sin x ) = \cos x-x\sin x$
Now, the second-order derivative is
$\frac{d^2y}{dx^2}= -\sin x-(\sin x+x\cos x) = -2\sin x - x\sin x$
Therefore, the second-order derivative is $\frac{d^2y}{dx^2}= -2\sin x - x\sin x$

Question:4 Find the second order derivatives of the functions given in Exercises 1 to 10.

$\log x$

Answer:

Given function is
$y=\log x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{1}{x}$
Now, second order derivative is
$\frac{d^2y}{dx^2}= \frac{-1}{x^2}$
Therefore, second order derivative is $\frac{d^2y}{dx^2}= \frac{-1}{x^2}$

Question:5 Find the second order derivatives of the functions given in Exercises 1 to 10.

$x ^3 \log x$

Answer:

Given function is
$y=x^3\log x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=3x^2.\log x+x^3.\frac{1}{x}= 3x^2.\log x+ x^2$
Now, the second-order derivative is
$\frac{d^2y}{dx^2}= 6x.\log x+3x^2.\frac{1}{x}+2x=6x.\log x+3x+2x = x(6.\log x+5)$
Therefore, the second-order derivative is $\frac{d^2y}{dx^2} = x(6.\log x+5)$

Question:6 Find the second order derivatives of the functions given in Exercises 1 to 10.

$e ^x \sin5 x$

Answer:

Given function is
$y= e^x\sin 5x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=e^x.\sin 5x +e^x.5\cos 5x = e^x(\sin5x+5\cos5x)$
Now, second order derivative is
$\frac{d^2y}{dx^2}= e^x(\sin5x+5\cos5x)+e^x(5\cos5x+5.(-5\sin5x))$
$= e^x(\sin5x+5\cos5x)+e^x(5\cos5x-25\sin5x)=e^x(10\cos5x-24\sin5x)$
$=2e^x(5\cos5x-12\sin5x)$
Therefore, second order derivative is $\frac{dy}{dx}=2e^x(5\cos5x-12\sin5x)$

Question:7 Find the second order derivatives of the functions given in Exercises 1 to 10.

$e ^{6x}\cos 3x$

Answer:

Given function is
$y= e^{6x}\cos 3x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=6e^{6x}.\cos 3x +e^{6x}.(-3\sin 3x)= e^{6x}(6\cos 3x-3\sin 3x)$
Now, second order derivative is
$\frac{d^2y}{dx^2}= 6e^{6x}(6\cos3x-3\sin3x)+e^{6x}(6.(-3\sin3x)-3.3\cos3x)$
$= 6e^{6x}(6\cos3x-3\sin3x)-e^{6x}(18\sin3x+9\cos3x)$
$e^{6x}(27\cos3x-36\sin3x) = 9e^{6x}(3\cos3x-4\sin3x)$
Therefore, second order derivative is $\frac{dy}{dx} = 9e^{6x}(3\cos3x-4\sin3x)$

Question:8 Find the second order derivatives of the functions given in Exercises 1 to 10.

$\tan ^{-1} x$

Answer:

Given function is
$y = \tan^{-1}x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(\tan^{-1}x)}{dx}=\frac{1}{1+x^2}$
Now, second order derivative is
$\frac{d^2y}{dx^2}= \frac{-1}{(1+x^2)^2}.2x = \frac{-2x}{(1+x^2)^2}$
Therefore, second order derivative is $\frac{d^2y}{dx^2} = \frac{-2x}{(1+x^2)^2}$

Question:9 Find the second order derivatives of the functions given in Exercises 1 to 10.

$\log (\log x )$

Answer:

Given function is
$y = \log(\log x)$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(\log(\log x))}{dx}=\frac{1}{\log x}.\frac{1}{x}= \frac{1}{x\log x}$
Now, second order derivative is
$\frac{d^2y}{dx^2}= \frac{-1}{(x\log x)^2}.(1.\log x+x.\frac{1}{x}) = \frac{-(\log x+1)}{(x\log x)^2}$
Therefore, second order derivative is $\frac{d^2y}{dx^2} = \frac{-(\log x+1)}{(x\log x)^2}$

Question:10 Find the second order derivatives of the functions given in Exercises 1 to 10.

$\sin (\log x )$

Answer:

Given function is
$y = \sin(\log x)$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(\sin(\log x))}{dx}=\cos (\log x).\frac{1}{x}= \frac{\cos (\log x)}{x}$
Now, second order derivative is
Using Quotient rule
$\frac{d^2y}{dx^2}=\frac{-\sin(\log x)\frac{1}{x}.x-\cos(\log x).1}{x^2} = \frac{-(\sin (\log x)+\cos(\log x))}{x^2}$
Therefore, second order derivative is $\frac{d^2y}{dx^2} = \frac{-(\sin (\log x)+\cos(\log x))}{x^2}$

Question:11 If $y = 5 \cos x - 3 \sin x$ prove that $\frac{d^2y}{dx^2}+y = 0$

Answer:

Given function is
$y = 5 \cos x - 3 \sin x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(5\cos x-3\sin x)}{dx}=-5\sin x-3\cos x$
Now, the second-order derivative is
$\frac{d^2y}{dx^2}=\frac{d^2(-5\sin x-3\cos x)}{dx^2}=-5\cos x+3\sin x$
Now,
$\frac{d^2y}{dx^2}+y=-5\cos x+3\sin x+5\cos x-3\sin x = 0$
Hence proved

Question:12 If $y = \cos ^{-1} x$ Find $\frac{d ^2 y }{dx^2 }$ in terms of y alone.

Answer:

Given function is
$y = \cos ^{-1} x$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d( \cos ^{-1} x)}{dx}=\frac{-1}{\sqrt{1-x^2}}$
Now, second order derivative is
$\frac{d^2y}{dx^2}=\frac{d^2(\frac{-1}{\sqrt{1-x^2}})}{dx^2}=\frac{-(-1)}{(\sqrt{1-x^2})^2}.(-2x) = \frac{-2x}{1-x^2}$ -(i)
Now, we want $\frac{d^2y}{dx^2}$ in terms of y
$y = \cos ^{-1} x$
$x = \cos y$
Now, put the value of x in (i)
$\frac{d^2y}{dx^2} = \frac{-2\cos y }{1-\cos^2 y } = \frac{-2\cos y}{\sin ^2 y}= -2\cot y cosec y$
$(\because 1-\cos^2x =\sin^2 x\ and \ \frac{\cos x}{\sin x} = \cot x \ and \ \frac{1}{\sin x}= cosec x)$
Therefore, answer is $\frac{d^2y}{dx^2} = -2\cot y cosec y$

Question:13 If $y = 3 \cos (\log x) + 4 \sin (\log x)$ , show that $x^2 y_2 + xy_1 + y = 0$

Answer:

Given function is
$y = 3 \cos (\log x) + 4 \sin (\log x)$
Now, differentiation w.r.t. x
$y_1=\frac{dy}{dx}=\frac{d( 3 \cos (\log x) + 4 \sin (\log x))}{dx}=-3\sin(\log x).\frac{1}{x}+4\cos (\log x).\frac{1}{x}$
$=\frac{4\cos (\log x)-3\sin(\log x)}{x}$ -(i)
Now, second order derivative is
By using the Quotient rule
$y_2=\frac{d^2y}{dx^2}=\frac{d^2(\frac{4\cos (\log x)-3\sin(\log x)}{x})}{dx^2}= \frac{(-4\sin(\log x).\frac{1}{x}-3\cos(\log x).\frac{1}{x}).x-1.(4\cos (\log x)-3\sin(\log x))}{x^2}$
$=\frac{-\sin(\log x)+7\cos (\log x)}{x^2}$ -(ii)
Now, from equation (i) and (ii) we will get $y_1 \ and \ y_2$
Now, we need to show
$x^2 y_2 + xy_1 + y = 0$
Put the value of $y_1 \ and \ y_2$ from equation (i) and (ii)
$x^2\left ( \frac{-\sin(\log x)+7\cos (\log x)}{x^2} \right )+x\left ( \frac{4\cos (\log x)-3\sin(\log x)}{x} \right )+ 3 \cos (\log x)$ $+4\sin(\log x)$
$-\sin(\log x)-7\cos(\log x)+4\cos(\log x)-3\sin(\log x)+3\ cos (\log x)$ $+4\sin(\log x)$
$=0$
Hence proved

Question:14 If $y = A e ^{mx} + Be ^{nx}$ , show that $\frac{d ^2 y}{dx^2} - (m+n) \frac{dy}{dx} + mny = 0$

Answer:

Given function is
$y = A e ^{mx} + Be ^{nx}$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(A e ^{mx} + Be ^{nx})}{dx}=mAe^{mx}+nBe^{nx}$ -(i)
Now, second order derivative is
$\frac{d^2y}{dx^2}=\frac{d^2(mAe^{mx}+nBe^{nx})}{dx^2}= m^2Ae^{mx}+n^2Be^{nx}$ -(ii)
Now, we need to show
$\frac{d ^2 y}{dx^2} - (m+n) \frac{dy}{dx} + mny = 0$
Put the value of $\frac{d^2y}{dx^2} \ and \ \frac{dy}{dx}$ from equation (i) and (ii)
$m^2Ae^{mx}+n^2Be^{nx}-(m+n)(mAe^{mx}+nBx^{nx}) +mn(Ae^{mx}+Be^{nx})$
$m^2Ae^{mx}+n^2Be^{nx}-m^2Ae^{mx}-mnBx^{nx}-mnAe^{mx} -n^2Be^{nx}+mnAe^{mx}$ $+mnBe^{nx}$
$=0$
Hence proved

Question:15 If $y = 500 e ^{7x} + 600 e ^{- 7x }$ , show that $\frac{d^2 y}{dx ^2} = 49 y$
Answer:

Given function is
$y = 500 e ^{7x} + 600 e ^{- 7x }$
Now, differentiation w.r.t. x
$\frac{dy}{dx}=\frac{d(500 e ^{7x} + 600 e ^{- 7x })}{dx}=7.500e^{7x}-7.600e^{-7x} =3500e^{7x}-4200e^{-7x}$ -(i)
Now, second order derivative is
$\frac{d^2y}{dx^2}=\frac{d^2(3500e^{7x}-4200e^{-7x})}{dx^2}$
$= 7.3500e^{7x}-(-7).4200e^{-7x}= 24500e^{7x}+29400e^{-7x}$ -(ii)
Now, we need to show
$\frac{d^2 y}{dx ^2} = 49 y$
Put the value of $\frac{d^2y}{dx^2}$ from equation (ii)
$24500e^{7x}+29400e^{-7x}=49(500e^{7x}+600e^{-7x})$
$= 24500e^{7x}+29400e^{-7x}$
Hence, L.H.S. = R.H.S.
Hence proved

Question:16 If $e ^y (x+1) = 1$ show that $\frac{d^2 y }{dx^2 } = (\frac{dy}{dx})^2$

Answer:

Given function is
$e ^y (x+1) = 1$
We can rewrite it as
$e^y = \frac{1}{x+1}$
Now, differentiation w.r.t. x
$\frac{d(e^y)}{dx}=\frac{d(\frac{1}{x+1})}{dx}\\ e^y.\frac{dy}{dx}= \frac{-1}{(x+1)^2}\\ \frac{1}{x+1}.\frac{dy}{dx}= \frac{-1}{(x+1)^2} \ \ \ \ \ \ \ \ \ (\because e^y = \frac{1}{x+1})\\ \frac{dy}{dx}= \frac{-1}{x+1}$ -(i)
Now, second order derivative is
$\frac{d^2y}{dx^2}=\frac{d^2(\frac{-1}{x+1})}{dx^2}=\frac{-(-1)}{(x+1)^2} = \frac{1}{(x+1)^2}$ -(ii)
Now, we need to show
$\frac{d^2 y }{dx^2 } = (\frac{dy}{dx})^2$
Put value of $\frac{d^2y}{dx^2} \ and \ \frac{dy}{dx}$ from equation (i) and (ii)
$\frac{1}{(x+1)^2}=\left ( \frac{-1}{x+1} \right )^2$
$=\frac{1}{(x+1)^2}$
Hence, L.H.S. = R.H.S.
Hence proved

Question:17 If $y = (\tan^{-1} x)^2$ show that $(x^2 + 1)^2 y_2 + 2x (x^2 + 1) y_1 = 2$

Answer:

Given function is
$y = (\tan^{-1} x)^2$
Now, differentiation w.r.t. x
$y_1=\frac{dy}{dx}=\frac{d((\tan^{-1}x)^2)}{dx}= 2.\tan^{-1}x.\frac{1}{1+x^2}= \frac{2\tan^{-1}x}{1+x^2}$ -(i)
Now, the second-order derivative is
By using the quotient rule
$y_2=\frac{d^2y}{dx^2}=\frac{d^2(\frac{2\tan^{-1}x}{1+x^2})}{dx^2}=\frac{2.\frac{1}{1+x^2}.(1+x^2)-2\tan^{-1}x(2x)}{(1+x^2)^2}=\frac{2-4x\tan^{-1}x}{(1+x^2)^2}$ -(ii)
Now, we need to show
$(x^2 + 1)^2 y_2 + 2x (x^2 + 1) y_1 = 2$
Put the value from equation (i) and (ii)
$(x^2+1)^2.\frac{2-4x\tan^{-1}x}{(1+x^2)^2}+2x(x^2+1).\frac{2\tan^{-1}x}{x^2+1}\\ \Rightarrow 2-4x\tan^{-1}x+4x\tan^{-1}x = 2$
Hence, L.H.S. = R.H.S.
Hence proved

Class 12 Maths Chapter 5 NCERT solutions: Excercise: 5.8

Question:1 Verify Rolle’s theorem for the function $f (x) = x^2 + 2x - 8, x \epsilon [- 4, 2].$

Answer:

According to Rolle's theorem function must be
a ) continuous in given closed interval say [x,y]
b ) differentiable in given open interval say (x,y)
c ) f(x) = f(y)
Then their exist a $c \ \epsilon \ (x,y)$ such that $f^{'}(c)= 0$
If all these conditions are satisfies then we can verify Rolle's theorem
Given function is
$f (x) = x^2 + 2x - 8$
Now, being a polynomial function, $f (x) = x^2 + 2x - 8$ is both continuous in [-4,2] and differentiable in (-4,2)
Now,
$f (-4) = (-4)^2 + 2(-4) - 8= 16-8-8=16-16=0$
Similalrly,
$f (2) = (2)^2 + 2(2) - 8= 4+4-8=8-8=0$
Therefore, value of $f (-4) = f(2)=0$ and value of f(x) at -4 and 2 are equal
Now,
According to roll's theorem their is point c , $c \ \epsilon (-4,2)$ such that $f^{'}(c)=0$
Now,
$f^{'}(x)=2x+2\\ f^{'}(c)=2c+2\\ f^{'}(c)=0\\ 2c+2=0\\ c = -1$
And $c = -1 \ \epsilon \ (-4,2)$
Hence, Rolle's theorem is verified for the given function $f (x) = x^2 + 2x - 8$

Question:2 (1) Examine if Rolle’s theorem is applicable to any of the following functions. Can
you say some thing about the converse of Rolle’s theorem from these example?
$f (x) = [x] \: \: for \: \: x \epsilon [ 5,9]$

Answer:

According to Rolle's theorem function must be
a ) continuous in given closed interval say [x,y]
b ) differentiable in given open interval say (x,y)
c ) f(x) = f(y)
Then their exist a $c \ \epsilon \ (x,y)$ such that $f^{'}(c)= 0$
If all these conditions are satisfied then we can verify Rolle's theorem
Given function is
$f (x) = [x]$
It is clear that Given function $f (x) = [x]$ is not continuous for each and every point in [5,9]
Now, lets check differentiability of f(x)
L.H.L. at x = n , $n \ \epsilon \ [5,9]$
$\lim_{h\rightarrow 0^-}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^-}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^-}\frac{n-1-n}{h} = \lim_{h\rightarrow 0^-}\frac{-1}{h}$ $= -\infty$
$( [n+h]=n-1 \because h < 0 \ therefore \ (n+h)<n)$
Now,
R.H.L. at x = n , $n \ \epsilon \ [5,9]$
$\lim_{h\rightarrow 0^+}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^+}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^+}\frac{n-n}{h} = \lim_{h\rightarrow 0^-}\frac{0}{h}=0$
$( [n+h]=n \because h > 0 \ therefore \ (n+h)>n)$
We can clearly see that R.H.L. is not equal to L.H.L.
Therefore, the function is not differential in (5,9)
Hence, Rolle's theorem is not applicable for given function $f (x) = [x]$ , $x \ \epsilon \ [5,9]$

Question:2 (2) Examine if Rolle’s theorem is applicable to any of the following functions. Can you say some thing about the converse of Rolle’s theorem from these example?

$f (x) = [x] \: \:for \: \: x \epsilon [ -2,2]$

Answer:

According to Rolle's theorem function must be
a ) continuous in given closed interval say [x,y]
b ) differentiable in given open interval say (x,y)
c ) f(x) = f(y)
Then their exist a $c \ \epsilon \ (x,y)$ such that $f^{'}(c)= 0$
If all these conditions are satisfies then we can verify Rolle's theorem
Given function is
$f (x) = [x]$
It is clear that Given function $f (x) = [x]$ is not continuous for each and every point in [-2,2]
Now, lets check differentiability of f(x)
L.H.L. at x = n , $n \ \epsilon \ [-2,2]$
$\lim_{h\rightarrow 0^-}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^-}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^-}\frac{n-1-n}{h} = \lim_{h\rightarrow 0^-}\frac{-1}{h}$ $= -\infty$
$( [n+h]=n-1 \because h < 0 \ therefore \ (n+h)<n)$
Now,
R.H.L. at x = n , $n \ \epsilon \ [-2,2]$
$\lim_{h\rightarrow 0^+}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^+}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^+}\frac{n-n}{h} = \lim_{h\rightarrow 0^-}\frac{0}{h}=0$
$( [n+h]=n \because h > 0 \ therefore \ (n+h)>n)$
We can clearly see that R.H.L. is not equal to L.H.L.
Therefore, function is not differential in (-2,2)
Hence, Rolle's theorem is not applicable for given function $f (x) = [x]$ , $x \ \epsilon \ [-2,2]$

Question:2 (3) Examine if Rolle’s theorem is applicable to any of the following functions. Can
you say some thing about the converse of Rolle’s theorem from these example?
$f (x) = x^2 - 1 \: \:for \: \: x \epsilon [ 1,2]$

Answer:

According to Rolle's theorem function must be
a ) continuous in given closed interval say [x,y]
b ) differentiable in given open interval say (x,y)
c ) f(x) = f(y)
Then there exist a $c \ \epsilon \ (x,y)$ such that $f^{'}(c)= 0$
If all these conditions are satisfied then we can verify Rolle's theorem
Given function is
$f (x) = x^2-1$
Now, being a polynomial , function $f (x) = x^2-1$ is continuous in [1,2] and differentiable in(1,2)
Now,
$f(1)=1^2-1 = 1-1 = 0$
And
$f(2)=2^2-1 = 4-1 = 3$
Therefore, $f(1)\neq f(2)$
Therefore, All conditions are not satisfied
Hence, Rolle's theorem is not applicable for given function $f (x) = [x]$ , $x \ \epsilon \ [-2,2]$

Question:3 If $f ; [ -5 ,5] \rightarrow R$ is a differentiable function and if $f ' (x)$ does not vanish
anywhere, then prove that $f (-5) \neq f(5)$

Answer:

It is given that
$f ; [ -5 ,5] \rightarrow R$ is a differentiable function
Now, f is a differential function. So, f is also a continuous function
We obtain the following results
a ) f is continuous in [-5,5]
b ) f is differentiable in (-5,5)
Then, by Mean value theorem we can say that there exist a c in (-5,5) such that
$f^{'}(c) = \frac{f(b)-f(a)}{b-a}$
$f^{'}(c) = \frac{f(5)-f(-5)}{5-(-5)}\\ f^{'}(c)= \frac{f(5)-f(-5)}{10}\\ 10f^{'}(c)= f(5)-f(-5)$
Now, it is given that $f ' (x)$ does not vanish anywhere
Therefore,
$10f^{'}(c)\neq 0\\ f(5)-f(-5) \neq 0\\ f(5)\neq f(-5)$
Hence proved

Question:4 Verify Mean Value Theorem, if $f (x) = x^2 - 4x - 3$ in the interval [a, b], where
a = 1 and b = 4.

Answer:

Condition for M.V.T.
If $f ; [ a ,b] \rightarrow R$
a ) f is continuous in [a,b]
b ) f is differentiable in (a,b)
Then, there exist a c in (a,b) such that
$f^{'}(c) = \frac{f(b)-f(a)}{b-a}$
It is given that
$f (x) = x^2 - 4x - 3$ and interval is [1,4]
Now, f is a polynomial function , $f (x) = x^2 - 4x - 3$ is continuous in[1,4] and differentiable in (1,4)
And
$f(1)= 1^2-4(1)-3= 1-7= -6$
and
$f(4)= 4^2-4(4)-3= 16-16-3= 16-19=-3$
Then, by Mean value theorem we can say that their exist a c in (1,4) such that
$f^{'}(c) = \frac{f(b)-f(a)}{b-a}$
$f^{'}(c) = \frac{f(4)-f(1)}{4-1}\\ f^{'}(c)= \frac{-3-(-6)}{3}\\ f^{'}(c)= \frac{3}{3}\\ f^{'}(c)= 1$
Now,
$f^{'}(x) =2x-4\\ f^{'}(c)-2c-4\\ 1=2c-4\\ 2c=5\\ c=\frac{5}{2}$
And $c=\frac{5}{2} \ \epsilon \ (1,4)$
Hence, mean value theorem is verified for the function $f (x) = x^2 - 4x - 3$

Question:5 Verify Mean Value Theorem, if $f (x) = x^3 - 5x^2- 3x$ in the interval [a, b], where
a = 1 and b = 3. Find all $c \epsilon (1,3)$ for which f '(c) = 0.

Answer:

Condition for M.V.T.
If $f ; [ a ,b] \rightarrow R$
a ) f is continuous in [a,b]
b ) f is differentiable in (a,b)
Then, their exist a c in (a,b) such that
$f^{'}(c) = \frac{f(b)-f(a)}{b-a}$
It is given that
$f (x) = x^3 - 5x^2- 3x$ and interval is [1,3]
Now, f being a polynomial function , $f (x) = x^3 - 5x^2- 3x$ is continuous in[1,3] and differentiable in (1,3)
And
$f(1)= 1^3-5(1)^2-3(1)= 1-5-3=1-8=-7$
and
$f(3)= 3^3-5(3)^2-3(3)= 27-5.9-9= 18-45=-27$
Then, by Mean value theorem we can say that their exist a c in (1,4) such that
$f^{'}(c) = \frac{f(b)-f(a)}{b-a}$
$f^{'}(c) = \frac{f(3)-f(1)}{3-1}\\ f^{'}(c)= \frac{-27-(-7)}{2}\\ f^{'}(c)= \frac{-20}{2}\\ f^{'}(c)= -10$
Now,
$f^{'}(x) =3x^2-10x-3\\ f^{'}(c)=3c^2-10c-3\\ -10=3c^2-10c-3\\ 3c^2-10c+7=0\\ 3c^2-3c-7c+7=0\\ (c-1)(3c-7)=0\\ c = 1 \ \ \ and \ \ \ c = \frac{7}{3}$
And $c=1,\frac{7}{3} \ and \ \frac{7}{3}\ \epsilon \ (1,3)$
Hence, mean value theorem is varified for following function $f (x) = x^3 - 5x^2- 3x$ and $c=\frac{7}{3}$ is the only point where f '(c) = 0

Question:6 Examine the applicability of Mean Value Theorem for all three functions given in
the above exercise 2.

Answer:

According to Mean value theorem function
$f:[a,b]\rightarrow R$ must be
a ) continuous in given closed interval say [a,b]
b ) differentiable in given open interval say (a,b)
Then their exist a $c \ \epsilon \ (x,y)$ such that
$f^{'}(c)= \frac{f(b)-f(a)}{b-a}$
If all these conditions are satisfies then we can verify mean value theorem
Given function is
$f (x) = [x]$
It is clear that Given function $f (x) = [x]$ is not continuous for each and every point in [5,9]
Now, lets check differentiability of f(x)
L.H.L. at x = n , $n \ \epsilon \ [5,9]$
$\lim_{h\rightarrow 0^-}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^-}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^-}\frac{n-1-n}{h} = \lim_{h\rightarrow 0^-}\frac{-1}{h}$ $= -\infty$
$( [n+h]=n-1 \because h < 0 \ therefore \ (n+h)<n)$
Now,
R.H.L. at x = n , $n \ \epsilon \ [5,9]$
$\lim_{h\rightarrow 0^+}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^+}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^+}\frac{n-n}{h} = \lim_{h\rightarrow 0^-}\frac{0}{h}=0$
$( [n+h]=n \because h > 0 \ therefore \ (n+h)>n)$
We can clearly see that R.H.L. is not equal to L.H.L.
Therefore, function is not differential in (5,9)
Hence, Mean value theorem is not applicable for given function $f (x) = [x]$ , $x \ \epsilon \ [5,9]$

Similaly,
Given function is
$f (x) = [x]$
It is clear that Given function $f (x) = [x]$ is not continuous for each and every point in [-2,2]
Now, lets check differentiability of f(x)
L.H.L. at x = n , $n \ \epsilon \ [-2,2]$
$\lim_{h\rightarrow 0^-}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^-}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^-}\frac{n-1-n}{h} = \lim_{h\rightarrow 0^-}\frac{-1}{h}$ $= -\infty$
$( [n+h]=n-1 \because h < 0 \ therefore \ (n+h)<n)$
Now,
R.H.L. at x = n , $n \ \epsilon \ [-2,2]$
$\lim_{h\rightarrow 0^+}\frac{f(n+h)-f(n)}{h} = \lim_{h\rightarrow 0^+}\frac{[n+h]-[n]}{h} = \lim_{h\rightarrow 0^+}\frac{n-n}{h} = \lim_{h\rightarrow 0^-}\frac{0}{h}=0$
$( [n+h]=n \because h > 0 \ therefore \ (n+h)>n)$
We can clearly see that R.H.L. is not equal to L.H.L.
Therefore, function is not differential in (-2,2)
Hence, Mean value theorem is not applicable for given function $f (x) = [x]$ , $x \ \epsilon \ [-2,2]$

Similarly,
Given function is
$f (x) = x^2-1$
Now, being a polynomial , function $f (x) = x^2-1$ is continuous in [1,2] and differentiable in(1,2)
Now,
$f(1)=1^2-1 = 1-1 = 0$
And
$f(2)=2^2-1 = 4-1 = 3$
Now,
$f^{'}(c)= \frac{f(b)-f(a)}{b-a}$
$f^{'}(c)= \frac{f(2)-f(1)}{2-1}\\ f^{'}(c)=\frac{3-0}{1}\\ f^{'}(c)= 3$
Now,
$f^{'}(x)= 2x\\ f^{'}(c)=2c\\ 3=2c\\ c=\frac{3}{2}$
And $c=\frac{3}{2} \ \epsilon \ (1,2)$
Therefore, mean value theorem is applicable for the function $f (x) = x^2-1$

NCERT class 12 continuity and differentiability ncert solutions Miscellaneous Excercise

Question:1 Differentiate w.r.t. x the function in Exercises 1 to 11.

$( 3x^2 - 9x + 5 )^9$

Answer:

Given function is
$f(x)=( 3x^2 - 9x + 5 )^9$
Now, differentiation w.r.t. x is
$f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d((3x^2-9x+5)^9)}{dx}= 9(3x^2-9x+5)^8.(6x-9)$
$= 27(2x-3)(3x^2-9x+5)^8$
Therefore, differentiation w.r.t. x is $27(3x^2-9x+5)^8(2x-3)$

Question:2 Differentiate w.r.t. x the function in Exercises 1 to 11.

$\sin ^3 x + \cos ^6 x$

Answer:

Given function is
$f(x)= \sin ^3 x + \cos ^6 x$
Now, differentiation w.r.t. x is
$f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\sin^3x +\cos^6x)}{dx}=3\sin^2x.\frac{d(\sin x)}{dx}+6\cos^5x.\frac{d(\cos x)}{dx}$
$=3\sin^2x.\cos x+6\cos^5x.(-\sin x)$
$=3\sin^2x\cos x- 6\cos^5x\sin x = 3\sin x\cos x(\sin x- 2\cos ^4x)$

Therefore, differentiation w.r.t. x is $3\sin x\cos x(\sin x- 2\cos ^4x)$

Question:3 Differentiate w.r.t. x the function in Exercises 1 to 11.

$( 5 x) ^{ 3 \cos 2x }$

Answer:

Given function is
$y=( 5 x) ^{ 3 \cos 2x }$
Take, log on both the sides
$\log y = 3\cos 2x\log 5x$
Now, differentiation w.r.t. x is
By using product rule
$\frac{1}{y}.\frac{dy}{dx} = 3.(-2\sin 2x)\log 5x + 3\cos 2x.\frac{1}{5x}.5= -6\sin2x\log 5x +\frac{3\cos 2x}{x}\\ \frac{dy}{dx} = y.\left ( -6\sin2x\log 5x +\frac{3\cos 2x}{x} \right )\\ \frac{dy}{dx} = (5x)^{3\cos 2x}.\left ( -6\sin2x\log 5x +\frac{3\cos 2x}{x} \right )$

Therefore, differentiation w.r.t. x is $(5x)^{3\cos 2x}.\left ( \frac{3\cos 2x}{x}-6\sin2x\log 5x \right )$

Question:4 Differentiate w.r.t. x the function in Exercises 1 to 11.

$\sin ^ {-1} (x \sqrt x ) , 0 \leq x\leq 1$

Answer:

Given function is
$f(x)=\sin ^ {-1} (x \sqrt x ) , 0 \leq x\leq 1$
Now, differentiation w.r.t. x is
$f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\sin^{-1}x\sqrt x)}{dx}=\frac{1}{\sqrt{1-(x\sqrt x)^2}}.\frac{d(x\sqrt x)}{dx}$
$=\frac{1}{\sqrt{1-x^3}}.\left ( 1.\sqrt x+x\frac{1}{2\sqrt x} \right )$
$=\frac{1}{\sqrt{1-x^3}}.\left ( \frac{3\sqrt x}{2} \right )$
$=\frac{3}{2}.\sqrt{\frac{x}{1-x^3}}$

Therefore, differentiation w.r.t. x is $\frac{3}{2}.\sqrt{\frac{x}{1-x^3}}$

Question:5 Differentiate w.r.t. x the function in Exercises 1 to 11.

$\frac{\cos ^{-1}x/2}{\sqrt {2x+7}} , -2 < x < 2$

Answer:

Given function is
$f(x)=\frac{\cos ^{-1}x/2}{\sqrt {2x+7}} , -2 < x < 2$
Now, differentiation w.r.t. x is
By using the Quotient rule
$f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\frac{\cos^{-1}\frac{x}{2}}{\sqrt{2x+7}})}{dx}=\frac{\frac{d(\cos^{-1}\frac{x}{2})}{dx}.\sqrt{2x+7}-\cos^{-1}\frac{x}{2}.\frac{d(\sqrt{2x+7})}{dx}}{(\sqrt{2x+7})^2}\\ f^{'}(x) = \frac{\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{1}{2}.\sqrt{2x+7}-\cos^{-1}\frac{x}{2}.\frac{1}{2.\sqrt{2x+7}}.2}{2x+7}\\ f^{'}(x)= -\left [\frac{1}{(\sqrt{4-x^2})(\sqrt{2x+7})}+\frac{\cos^{-1}\frac{x}{2}}{(2x+7)^\frac{3}{2}} \right ]$

Therefore, differentiation w.r.t. x is $-\left [\frac{1}{(\sqrt{4-x^2})(\sqrt{2x+7})}+\frac{\cos^{-1}\frac{x}{2}}{(2x+7)^\frac{3}{2}} \right ]$

Question:6 Differentiate w.r.t. x the function in Exercises 1 to 11.

$\cot ^{-1} \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ] , 0 < x < \pi /2$

Answer:

Given function is
$f(x)=\cot ^{-1} \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ] , 0 < x < \pi /2$
Now, rationalize the [] part
$\left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ]= \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} .\frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}\right ]$

$=\frac{(\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x })^2}{(\sqrt{1+\sin x})^2-(\sqrt{1-\sin x})^2} \ \ \ \ \ \ (Using \ (a-b)(a+b)=a^2-b^2)$

$=\frac{((\sqrt { 1+ \sin x })^2+ (\sqrt { 1- \sin x })^2+2(\sqrt { 1+ \sin x })(\sqrt { 1- \sin x }))}{1+\sin x-1+\sin x}$
$(Using \ (a+b)^2=a^2+b^2+2ab)$
$=\frac{1+\sin x+1-\sin x+2\sqrt{1-\sin^2x} }{2\sin x}$

$=\frac{2(1+\cos x)}{2\sin x} = \frac{1+\cos x}{\sin x}$

$=\frac{2\cos^2\frac{x}{2}}{2\sin\frac{x}{2}\cos\frac{x}{2}} \ \ \ \ \ (\because 2\cos^2= 1+\cos2x \ and \ \sin2x = 2\sin x\cos x)$

$=\frac{2\cos\frac{x}{2}}{2\sin\frac{x}{2}} = \cot \frac{x}{2}$
Given function reduces to
$f(x) = \cot^{-1}(\cot \frac{x}{2})\\ f(x) = \frac{x}{2}$
Now, differentiation w.r.t. x is
$f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\frac{x}{2})}{dx} = \frac{1}{2}$
Therefore, differentiation w.r.t. x is $\frac{1}{2}$

Question:7 Differentiate w.r.t. x the function in Exercises 1 to 11. $( \log x )^{ \log x } , x > 1$

Answer:

Given function is
$y=( \log x )^{ \log x } , x > 1$
Take log on both sides
$\log y=\log x\log( \log x )$
Now, differentiate w.r.t.
$\frac{1}{y}.\frac{dy}{dx}= \frac{1}{x}.\log (\log x)+\log x.\frac{1}{\log x}.\frac{1}{x} = \frac{\log x+1}{x}$
$\frac{dy}{dx} = y.\left ( \frac{\log x+1}{x} \right )\\$
$\frac{dy}{dx} = (\log x)^{\log x}.\left ( \frac{\log x+1}{x} \right )\\$
Therefore, differentiation w.r.t x is $(\log x)^{\log x}.\left ( \frac{\log x+1}{x} \right )\\$

Question:8 $\cos ( a \cos x + b \sin x )$ , for some constant a and b.

Answer:

Given function is
$f(x)=\cos ( a \cos x + b \sin x )$
Now, differentiation w.r.t x
$f^{'}(x)= \frac{d(f(x))}{dx}= \frac{d(\cos(a\cos x+ b \sin x))}{dx}$
$= -\sin(a\cos x+b\sin x).\frac{d(a\cos x+b\sin x)}{dx}$
$= -\sin(a\cos x+b\sin x).(-a\sin x+b\cos x)$
$= (a\sin x-b\cos x)\sin(a\cos x+b\sin x).$
Therefore, differentiation w.r.t x $(a\sin x-b\cos x)\sin(a\cos x+b\sin x)$

Question: 9 $(\sin x - \cos x)^{ (\sin x - \cos x), } , \frac{\pi }{4} <x<\frac{3 \pi }{4}$

Answer:

Given function is
$y=(\sin x - \cos x)^{ (\sin x - \cos x), } , \frac{\pi }{4} <x<\frac{3 \pi }{4}$
Take log on both the sides
$\log y=(\sin x - \cos x)\log (\sin x - \cos x)$
Now, differentiate w.r.t. x
$\frac{1}{y}.\frac{dy}{dx} = \frac{d(\sin x-\cos x)}{dx}.\log(\sin x- \cos x)+(\sin x- \cos x).\frac{d(\log(\sin x- \cos x))}{dx}$
$\frac{1}{y}.\frac{dy}{dx} =(\cos x -(-\sin x)).\log(\sin x-\cos x)+(\sin x- \cos x).\frac{(\cos x -(-\sin x))}{(\sin x- \cos x)}$
$\frac{dy}{dx} =y.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right )$
$\frac{dy}{dx} =(\sin x-\cos x)^{(\sin x-\cos x)}.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right )$
Therefore, differentiation w.r.t x is $(\sin x-\cos x)^{(\sin x-\cos x)}.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right ), sinx>cosx$

Question:10 $x ^x + x ^a + a ^x + a ^a$ , for some fixed a > 0 and x > 0

Answer:

Given function is
$f(x)=x ^x + x ^a + a ^x + a ^a$
Lets take
$u = x^x$
Now, take log on both sides
$\log u = x \log x$
Now, differentiate w.r.t x
$\frac{1}{u}.\frac{du}{dx}= \frac{dx}{dx}.\log x+x.\frac{d(\log x)}{dx}\\ \\ \frac{1}{u}.\frac{du}{dx}= 1.\log x+x.\frac{1}{x}\\ \\ \frac{du}{dx}= y.(\log x+1)\\ \\ \frac{du}{dx}= x^x.(\log x+1)$ -(i)
Similarly, take $v = x^a$
take log on both the sides
$\log v = a\log x$
Now, differentiate w.r.t x
$\frac{1}{v}.\frac{dv}{dx}= a.\frac{d(\log x)}{dx}=a.\frac{1}{x}= \frac{a}{x}\\ \\ \frac{dv}{dx}= v.\frac{a}{x}\\ \\ \frac{dv}{dx}= x^a.\frac{a}{x}$ -(ii)

Similarly, take $z = a^x$
take log on both the sides
$\log z = x\log a$
Now, differentiate w.r.t x
$\frac{1}{z}.\frac{dz}{dx}=\log a.\frac{d(x)}{dx}=\log a.1= \log a\\ \\ \frac{dz}{dx}= z.\log a\\ \\ \frac{dz}{dx}= a^x.\log a$ -(iii)

Similarly, take $w = a^a$
take log on both the sides
$\log w = a\log a= \ constant$
Now, differentiate w.r.t x
$\frac{1}{w}.\frac{dw}{dx}= a.\frac{d(a\log a)}{dx}= 0\\ \\ \frac{dw}{dx} = 0$ -(iv)
Now,
$f(x)=u+v+z+w$
$f^{'}(x) = \frac{du}{dx}+\frac{dv}{dx}+\frac{dz}{dx}+\frac{dw}{dx}$
Put values from equation (i) , (ii) ,(iii) and (iv)
$f^{'}(x)= x^x(\log x+1)+ax^{a-1}+a^x\log a$
Therefore, differentiation w.r.t. x is $x^x(\log x+1)+ax^{a-1}+a^x\log a$

Question: 11 $x ^{x^2 -3} + ( x-3 ) ^{x^2} , for\: \: x > 3$

Answer:

Given function is
$f(x)=x ^{x^2 -3} + ( x-3 ) ^{x^2} , for\: \: x > 3$
take $u=x ^{x^2 -3}$
Now, take log on both the sides
$\log u=(x^2-3)\log x$
Now, differentiate w.r.t x
$\frac{1}{u}.\frac{du}{dx}= \frac{d(x^2-3)}{dx}.\log x+(x^2-3).\frac{d(\log x)}{dx}\\ \\ \frac{1}{u}.\frac{du}{dx} = 2x.\log x+(x^2-3).\frac{1}{x}\\ \\ \frac{1}{u}.\frac{du}{dx} = \frac{2x^2\log x+x^2-3}{x}\\ \\ \frac{du}{dx}= u.\left ( \frac{2x^2\log x+x^2-3}{x} \right )\\ \\ \frac{du}{dx}= x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )\\ \\$ -(i)
Similarly,
take $v=(x-3)^x^2\\$
Now, take log on both the sides
$\log v=x^2\log (x-3)$
Now, differentiate w.r.t x
$\frac{1}{v}.\frac{dv}{dx}= \frac{d(x^2)}{dx}.\log (x-3)+x^2.\frac{d(\log (x-3))}{dx}\\ \\ \frac{1}{v}.\frac{dv}{dx} = 2x.\log (x-3)+x^2.\frac{1}{(x-3)}\\ \\ \frac{1}{v}.\frac{dv}{dx} = 2x\log(x-3)+\frac{x^2}{x-3}\\ \\ \frac{dv}{dx}= v.\left ( 2x\log(x-3)+\frac{x^2}{x-3} \right )\\ \\ \frac{dv}{dx}= (x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )\\ \\$ -(ii)
Now
$f(x)= u + v$
$f^{'}(x)= \frac{du}{dx}+\frac{dv}{dx}$
Put the value from equation (i) and (ii)
$f^{'}(x)= x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )+(x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )$
Therefore, differentiation w.r.t x is $x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )+(x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )$

Question:12 Find dy/dx if $y = 12 (1 - \cos t), x = 10 (t - \sin t),$ $-\frac{\pi }{2} <t< \frac{\pi }{2}$

Answer:

Given equations are
$y = 12 (1 - \cos t), x = 10 (t - \sin t),$
Now, differentiate both y and x w.r.t t independently
$\frac{dy}{dt}=\frac{d(12(1-\cos t))}{dt}= -12(-\sin t)=12\sin t$
And
$\frac{dx}{dt}=\frac{d(10(t-\sin t))}{dt}= 10-10\cos t$
Now
$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{12\sin t}{10(1-\cos t)} = \frac{6}{5}.\frac{2\sin \frac{t}{2}\cos \frac{t}{2}}{2\sin^2\frac{t}{2}} = \frac{6}{5}.\frac{\cos \frac{t}{2}}{\sin \frac{t}{2}}\\ \\$
$(\because \sin 2x = 2\sin x\cos x \ and \ 1-\cos 2x = 2\sin^2x)$
$\frac{dy}{dx}=\frac{6}{5}.\cot \frac{t}{2}$
Therefore, differentiation w.r.t x is $\frac{6}{5}.\cot \frac{t}{2}$

Question:13 Find dy/dx if $y = sin ^{-1} x + sin^{-1} \sqrt{1- x^2} , 0 <x< 1$

Answer:

Given function is
$y = sin ^{-1} x + sin^{-1} \sqrt{1- x^2} , 0 <x< 1$
Now, differentiatiate w.r.t. x
$\frac{dy}{dx}= \frac{d(sin ^{-1} x + sin^{-1} \sqrt{1- x^2})}{dx} = \frac{1}{\sqrt{1-x^2}}+\frac{1}{\sqrt{1-(\sqrt{1-x^2})^2}}.\frac{d(\sqrt{1-x^2})}{dx}\\ \frac{dy}{dx}= \frac{1}{\sqrt{1-x^2}}+\frac{1}{\sqrt{1-1+x^2}}.\frac{1}{2\sqrt{1-x^2}}.(-2x)\\ \\ \frac{dy}{dx}= \frac{1}{\sqrt{1-x^2}}-\frac{1}{\sqrt{1-x^2}}\\ \frac{dy}{dx}= 0$
Therefore, differentiatiate w.r.t. x is 0

Question:14 If $x \sqrt {1+ y }+ y \sqrt { 1+ x } = 0 \: \: for \: \: , -1 < x < 1 \: \:prove \: \: that \: \frac{dy}{dx} = -\frac{1}{(1+x)^2}$

Answer:

Given function is
$x \sqrt {1+ y }+ y \sqrt { 1+ x } = 0$
$x\sqrt{1+y} = - y\sqrt{1+x}$
Now, squaring both sides
$(x\sqrt{1+y})^2 = (- y\sqrt{1+x})^2\\ x^2(1+y)=y^2(1+x)\\ x^2+x^2y=y^2x+y^2\\ x^2-y^2=y^2x-x^2y\\ (x-y)(x+y) = -xy(x-y) \\ x+y =-xy\\ y = \frac{-x}{1+x}$
Now, differentiate w.r.t. x is
$\frac{dy}{dx} = \frac{d(\frac{-x}{1+x})}{dx}= \frac{-1.(1+x)-(-x).(1)}{(1+x)^2}= \frac{-1}{(1+x)^2}$
Hence proved

Question:15 If $(x - a)^2 + (y - b)^2 = c^2$ , for some c > 0, prove that $\frac{\left [ 1+(\frac{dy}{dx} )^2 \right ]^{3/2}}{\frac{d^2 y }{dx^2}}\:$ is a constant independent of a and b.

Answer:

Given function is
$(x - a)^2 + (y - b)^2 = c^2$
$(y - b)^2 = c^2-(x - a)^2$ - (i)
Now, differentiate w.r.t. x
$\frac{d((x-a)^2)}{dx}+\frac{((y-b)^2)}{dx}=\frac{d(c^2)}{dx}\\ \\ 2(x-a)+2(y-b).\frac{dy}{dx}=0\\ \\ \frac{dy}{dx} = \frac{a-x}{y-b}$ -(ii)
Now, the second derivative
$\frac{d^2y}{dx^2} = \frac{\frac{d(a-x)}{dx}.(y-b) -(a-x).\frac{d(y-b)}{dx}}{(y-b)^2}\\ \\ \frac{d^2y}{dx^2} =\frac{ (-1).(y-b)-(a-x).\frac{dy}{dx}}{(y-b)^2}\\ \\$
Now, put values from equation (i) and (ii)
$\frac{d^2y}{dx^2} =\frac{-(y-b)-(a-x).\frac{a-x}{y-b}}{(y-b)^2}\\ \\ \frac{d^2y}{dx^2} = \frac{-((y-b)^2+(a-x)^2)}{(y-b)^\frac{3}{2}} = \frac{-c^2}{(y-b)^\frac{3}{2}}$ $(\because (x - a)^2 + (y - b)^2 = c^2)$
Now,
$\frac{\left [ 1+(\frac{dy}{dx} )^2 \right ]^{3/2}}{\frac{d^2 y }{dx^2}} = \frac{\left ( 1+\left ( \frac{x-a}{y-b} \right )^2 \right )^\frac{3}{2}}{\frac{-c^2}{(y-b)^\frac{3}{2}}} = \frac{\frac{\left ( (y-b)^2 +(x-a)^2\right )^\frac{3}{2}}{(y-b)^\frac{3}{2}}}{\frac{-c^2}{(y-b)^\frac{3}{2}}} = \frac{(c^2)^\frac{3}{2}}{-c^2}= \frac{c^3}{-c^2}= c$ $(\because (x - a)^2 + (y - b)^2 = c^2)$
Which is independent of a and b
Hence proved

Question:16 If $\cos y = x \cos (a + y)$ , with $\cos a \neq \pm 1$ , prove that $\frac{dy}{dx} = \frac{\cos ^2 (a+y )}{\sin a }$

Answer:

Given function is
$\cos y = x \cos (a + y)$
Now, Differentiate w.r.t x
$\frac{d(\cos y)}{dx} = \frac{dx}{dx}.\cos(a+y)+x.\frac{d(\cos (a+y))}{dx}\\ \\ -\sin y \frac{dy}{dx} = 1.\cos (a+y)+x.(-\sin(a+y)).\frac{dy}{dx}\\ \\ \frac{dy}{dx}.(x\sin(a+y)-\sin y)= \cos(a+y)\\ \\ \frac{dy}{dx}.(\frac{\cos y}{\cos (a+b)}.\sin(a+y)-\sin y)= \cos(a+b) \ \ \ \ \ (\because x = \frac{\cos y}{\cos (a+b)})\\ \\ \frac{dy}{dx}.(\cos y\sin(a+y)-\sin y\cos(a+y))=\cos^2(a+b)\\ \\ \frac{dy}{dx}.(\sin(a+y-y))=\cos^2(a+b) \ \ \ \ \ \ \ (\because \cos A\sin B-\sin A\cos B = \sin(A-B))\\ \\ \frac{dy}{dx}= \frac{\cos^2(a+y)}{\sin a}$
Hence proved

Question:17 If $x = a (\cos t + t \sin t)$ and $y = a (\sin t - t \cos t),$ find $\frac{d^2 y }{dx^2 }$

Answer:

Given functions are
$x = a (\cos t + t \sin t)$ and $y = a (\sin t - t \cos t)$
Now, differentiate both the functions w.r.t. t independently
We get
$\frac{dx}{dt} = \frac{d(a(\cos t +t\sin t))}{dt}= a(-\sin t)+a(\sin t+t\cos t)$
$=-a\sin t+a\sin t+at\cos t = at\cos t$
Similarly,
$\frac{dy}{dt} = \frac{d(a(\sin t - t\cos t))}{dt}= a\cos t -a(\cos t+t(-\sin t))$
$= a\cos t -a\cos t+at\sin t =at\sin t$
Now,
$\frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{at\sin t}{at \cos t} = \tan t$
Now, the second derivative
$\frac{d^2y}{dx^2}=\frac{d}{dx}\frac{dy}{dx}= \sec^2 t.\frac{dt}{dx}=\frac{\sec^2t.\sec t }{at}=\frac{\sec^3t}{at}$
$(\because \frac{dx}{dt} = at\cos t \Rightarrow \frac{dt}{dx}= \frac{1}{at\cos t}=\frac{\sec t}{at})$
Therefore, $\frac{d^2y}{dx^2}=\frac{\sec^3t}{at}$

Question:18 If $f (x) = |x|^3$ , show that f ''(x) exists for all real x and find it.

Answer:

Given function is
$f (x) = |x|^3$
$f(x)\left\{\begin{matrix} -x^3 & x<0\\ x^3 & x>0 \end{matrix}\right.$
Now, differentiate in both the cases
$f(x)= x^3\\ f^{'}(x)=3x^2\\ f^{''}(x)= 6x$
And
$f(x)= -x^3\\ f^{'}(x)=-3x^2\\ f^{''}(x)= -6x$
In both, the cases f ''(x) exist
Hence, we can say that f ''(x) exists for all real x
and values are
$f^{''}(x)\left\{\begin{matrix} -6x &x<0 \\ 6x& x>0 \end{matrix}\right.$

Question:19 Using mathematical induction prove that $\frac{d}{dx} (x^n) = nx ^{n-1}$ for all positive integers n.

Answer:

Given equation is
$\frac{d}{dx} (x^n) = nx ^{n-1}$
We need to show that $\frac{d}{dx} (x^n) = nx ^{n-1}$ for all positive integers n
Now,
For ( n = 1) $\Rightarrow \frac{d(x^{1})}{dx}= 1.x^{1-1}= 1.x^0=1$
Hence, true for n = 1
For (n = k) $\Rightarrow \frac{d(x^{k})}{dx}= k.x^{k-1}$
Hence, true for n = k
For ( n = k+1) $\Rightarrow \frac{d(x^{k+1})}{dx}= \frac{d(x.x^k)}{dx}$
$= \frac{d(x)}{dx}.x^k+x.\frac{d(x^k)}{dx}$
$= 1.x^k+x.(k.x^{k-1}) = x^k+k.x^k= (k+1)x^k$
Hence, (n = k+1) is true whenever (n = k) is true
Therefore, by the principle of mathematical induction we can say that $\frac{d}{dx} (x^n) = nx ^{n-1}$ is true for all positive integers n

Question:20 Using the fact that $\sin (A + B) = \sin A \cos B + \cos A \sin B$ and the differentiation,
obtain the sum formula for cosines.

Answer:

Given function is
$\sin (A + B) = \sin A \cos B + \cos A \sin B$
Now, differentiate w.r.t. x
$\frac{d(\sin(A+B))}{dx} = \frac{d\sin A}{dx}.\cos B+\sin A.\frac{d\cos B}{dx}+\frac{d\cos A}{dx}.\sin B+\cos A.\frac{d\sin B}{dx}$
$\cos (A+b)\frac{d(A+B)}{dx}$ $=\frac{dA}{dx}(\cos A\cos B-\sin A\cos B)+\frac{dB}{dx}(\cos A \sin B-\sin A\sin B)$
$=(\cos A \sin B-\sin A\sin B).\frac{d(A+B)}{dx}$
$\cos(A+B)= \cos A\sin B-\sin A\cos B$
Hence, we get the formula by differentiation of sin(A + B)

Question:21 Does there exist a function which is continuous everywhere but not differentiable
at exactly two points? Justify your answer.

Answer:

Consider f(x) = |x| + |x +1|
We know that modulus functions are continuous everywhere and sum of two continuous function is also a continuous function
Therefore, our function f(x) is continuous
Now,
If Lets differentiability of our function at x = 0 and x= -1
L.H.D. at x = 0
$\lim_{h\rightarrow 0^-}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^-}\frac{f(h)-f(0)}{h}= \lim_{h\rightarrow 0^-}\frac{|h|+|h+1|-|1|}{h}$
$=\lim_{h\rightarrow 0^-}\frac{-h-(h+1)-1}{h}= 0$ $(|h| = - h \ because\ h < 0)$
R.H.L. at x = 0
$\lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^+}\frac{f(h)-f(0)}{h}= \lim_{h\rightarrow 0^+}\frac{|h|+|h+1|-|1|}{h}$
$=\lim_{h\rightarrow 0^+}\frac{h+h+1-1}{h}= \lim_{h\rightarrow 0^+}\frac{2h}{h}= 2$ $(|h| = h \ because \ h > 0)$
R.H.L. is not equal to L.H.L.
Hence.at x = 0 is the function is not differentiable
Now, Similarly
R.H.L. at x = -1
$\lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^+}\frac{f(-1+h)-f(-1)}{h}= \lim_{h\rightarrow 0^+}\frac{|-1+h|+|h|-|-1|}{h}$
$=\lim_{h\rightarrow 0^+}\frac{1-h+h-1}{h}= \lim_{h\rightarrow 0^+}\frac{0}{h}= 0$ $(|h| = h \ because \ h > 0)$
L.H.L. at x = -1
$\lim_{h\rightarrow 0^-}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h}= \lim_{h\rightarrow 0^-}\frac{|-1+h|+|h|-|1|}{h}$
$=\lim_{h\rightarrow 1^+}\frac{1-h-h-1}{h}= \lim_{h\rightarrow 0^+}\frac{-2h}{h}= -2$ $(|h| = - h \ because\ h < 0)$
L.H.L. is not equal to R.H.L, so not differentiable at x=-1

Hence, exactly two points where it is not differentiable

Question:22 If $y = \begin{vmatrix} f (x) & g(x) & h (x) \\ l& m &n \\ a& b &c \end{vmatrix}$ , prove that $dy/dx = \begin{vmatrix} f '(x) & g'(x) & h' (x) \\ l& m &n \\ a& b &c \end{vmatrix}$

Answer:

Given that
$y = \begin{vmatrix} f (x) & g(x) & h (x) \\ l& m &n \\ a& b &c \end{vmatrix}$
We can rewrite it as
$y = f(x)(mc-bn)-g(x)(lc-an)+h(x)(lb-am)$
Now, differentiate w.r.t x
we will get
$\frac{dy}{dx} = f^{'}(x)(mc-bn)-g^{'}(x)(lc-an)+h^{'}(x)(lb-am) \Rightarrow \begin{bmatrix} f^{'}(x) &g^{'}(x) &h^{'}(x) \\ l&m &n \\ a& b &c \end{bmatrix}$
Hence proved

Question:23 If 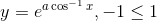$y = e ^{a \cos ^{-1}x} , -1 \leqx \leq 1$ , show that $( 1- x^2 ) \frac{d^2 y }{dx ^2} - x \frac{dy}{dx} - a ^2 y = 0$

Answer:

Given function is
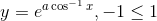
$y = e ^{a \cos ^{-1}x} , -1 \leqx \leq 1$

Now, differentiate w.r.t x we will get
$\frac{dy}{dx}= \frac{d(e^{a\cos^{-1}x})}{dx}.\frac{d(a\cos^{-1}x)}{dx} = e^{a\cos^{-1}x}.\frac{-a}{\sqrt{1-x^2}}$ -(i)
Now, again differentiate w.r.t x
$\frac{d^2y}{dx^2}= \frac{d}{dx}\frac{dy}{dx}= \frac{-ae^{a\cos^{-1}x}.\frac{-a}{\sqrt{1-x^2}}.\sqrt{1-x^2}+ae^{a\cos^{-1}x}.\frac{1.(-2x)}{2\sqrt{1-x^2}}}{(\sqrt{1-x^2})^2}$
$=\ \frac{a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}}{1-x^2}$ -(ii)
Now, we need to show that
$( 1- x^2 ) \frac{d^2 y }{dx ^2} - x \frac{dy}{dx} - a ^2 y = 0$
Put the values from equation (i) and (ii)
$(1-x^2).\left ( \ \frac{a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}}{1-x^2} \right )-x.\left ( \frac{-ae^{a\cos^{-1}x}}{\sqrt{1-x^2}} \right )-a^2e^{a\cos^{-1}x}$
$a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}+\left ( \frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}} \right )-a^2e^{a\cos^{-1}x} = 0$
Hence proved

If you are looking for continuity and differentiability class 12 NCERT solutions of exercises then these are listed below.

Topics of NCERT class 12 maths chapter 5 Continuity and Differentiability

5.1 Introduction

5.2 Continuity

5.2.1 Algebra of continuous functions

5.3. Differentiability

5.3.1 Derivatives of composite functions

5.3.2 Derivatives of implicit functions

5.3.3 Derivatives of inverse trigonometric functions

5.4 Exponential and Logarithmic Functions

5.5. Logarithmic Differentiation

5.6 Derivatives of Functions in Parametric Form

The mathematical definition of Continuity and Differentiability -

Let f be a real function and c be a point in the domain of f. Then f is continuous at c if $\lim_{x\rightarrow c}f(x)=f(c)$ . A function f is differentiable at point c in its domain if it is continuous at point c. A function is said to be differentiable in an interval [a, b] if it is differentiable at every point of [a, b].

'Continuity and differentiability' is one of the very important and time-consuming chapters of the NCERT Class 12 maths syllabus. It contains 8 exercises with 121 questions and also 23 questions in the miscellaneous exercise. In this article, you will find all NCERT solutions for class 12 maths chapter 5 continuity and differentiability including miscellaneous exercises.

Also read,

NCERT exemplar solutions class 12 maths chapter 5

NCERT class 12 maths ch 5 question answer - Topics

The main topics covered in chapter 5 maths class 12 are:

Continuity

A function is continuous at a given point if the left-hand limit, right-hand limit and value of function exist and are equal. In this class 12 NCERT topics elaborate concepts related to continuity, point of discontinuity, algebra of continuous function. Continuity and Differentiability class 12 solutions include a comprehensive module of quality questions.

Differentiability

This ch 5 maths class 12 discuss differentiability concepts of different functions including derivatives of composite functions, derivatives of implicit functions, derivatives of inverse trigonometric functions. To get command on these concepts you can refer to NCERT solutions for class 12 maths chapter 5.

Exponential and Logarithmic Functions

This ch 5 maths class 12 also includes concepts of exponential and logarithmic functions including natural log and their graphical representation. maths class 12 chapter 5 also contains fundamental properties of the logarithmic function. You can refer to class 12 NCERT solutions for questions about these concepts.

Logarithmic Differentiation

this class 12 ncert chapter discusses a special technique of differentiation known as logarithmic differentiation. to get command of these concepts you can go through the NCERT solution for class 12 maths chapter 5.

Derivatives of Functions in Parametric Forms

concepts to differentiate a function which is not implicit and explicit but given in the parametric form are explained in this chapter. Continuity and Differentiability class 12 solutions include problems to understand the concepts.

ch 5 maths class 12 also discuss in detail the concepts of second-order derivative, mean value theorem, Rolle's theorem. for questions on these concepts, you can browse NCERT solutions for class 12 chapter 5.

Topics enumerated in class 12 NCERT are very important and students are suggested to go through all the concepts discussed in the topics. Questions related to all the above topics are covered in the NCERT solutions for class 12 maths chapter 5

Also read,

NCERT solutions for class 12 maths - Chapter wise

Chapter 1	NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
Chapter 2	NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
Chapter 3	NCERT solutions for class 12 maths chapter 3 Matrices
Chapter 4	NCERT solutions for class 12 maths chapter 4 Determinants
Chapter 5	NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
Chapter 6	NCERT solutions for class 12 maths chapter 6 Application of Derivatives
Chapter 7	NCERT solutions for class 12 maths chapter 7 Integrals
Chapter 8	NCERT solutions for class 12 maths chapter 8 Application of Integrals
Chapter 9	NCERT solutions for class 12 maths chapter 9 Differential Equations
Chapter 10	NCERT solutions for class 12 maths chapter 10 Vector Algebra
Chapter 11	NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
Chapter 12	NCERT solutions for class 12 maths chapter 12 Linear Programming
Chapter 13	NCERT solutions for class 12 maths chapter 13 Probability

NCERT solutions for class 12 subject wise

NCERT Solutions class wise

NCERT Books and NCERT Syllabus

Tips to Use NCERT Solutions for Class 12 Maths Chapter 5

NCERT solutions for class 12 maths chapter 5 continuity and differentiability are very helpful in the preparation of this chapter. But here are some tips to get command on this chapter.

You should make sure that concepts related to 'limit' are clear to you as it forms the base for continuity.
First, go for the theorem and solved examples of continuity given in the NCERT textbook then try to solve exercise questions. You may find some difficulties in solving them. Go through the NCERT solutions for class 12 maths chapter 5 continuity and differentiability, it will help you to understand the concepts in a much easy way.
This chapter seems very easy but at the same time, the chances of silly mistakes are also high. So, it is advised to understand the theory and concepts properly before practicing questions of NCERT.
Once you are good in continuity, then go for the differentiability. Practice more and more questions to get command on it.
Differentiation is mostly formula-based, so practice NCERT questions, it won't take much effort to remember the formulas.

Also check,

Happy learning!!!

Frequently Asked Question (FAQs)

1. What are the important topics in chapter Continuity and Differentiability?

Basic concepts of continuity and differentiability, derivatives of composite functions, derivatives of implicit functions, derivatives of inverse trigonometric functions, exponential and logarithmic functions, logarithmic differentiation, derivatives of functions in parametric form are the important topics in this chapter. Practice these class 12 maths ch 5 question answer to command the concepts.

2. What are the reasons to opt for ncert continuity and differentiability solution?

The maths chapter 5 class 12 NCERT solutions created by the experts at Careers360 offer numerous advantages to students preparing for their board exams. These solutions provide comprehensive explanations of each topic, which help students achieve high scores. Additionally, the solutions are based on the latest CBSE syllabus for the 2022-23 academic year. Furthermore, these solutions also assist students in preparing for other competitive exams such as JEE Main and JEE Advanced. For ease, Students can study continuity and differentiability pdf both online and offline

3. Which is the best book for CBSE class 12 maths ?

NCERT is the best book for CBSE class 12 maths. Most of the questions in CBSE board exam are directly asked from NCERT textbook. All you need to do is rigorous practice of all the problems given in the NCERT textbook.

4. How many exercises are included in ncert solutions class 12 maths chapter 5?

According to the given information, there are 8 exercises in NCERT Solutions for maths chapter 5 class 12 . The following is the number of questions in each exercise:

Exercise 5.1: 34 questions
Exercise 5.2: 10 questions
Exercise 5.3: 15 questions
Exercise 5.4: 10 questions
Exercise 5.5: 18 questions
Exercise 5.6: 11 questions
Exercise 5.7: 17 questions
Exercise 5.8: 6 questions

Additionally, there is a Miscellaneous Exercise with 23 questions.

5. What is the weightage of the chapter Continuity and Differentiability for CBSE board exam ?

Generally, Continuity and differntiability has 9% weightage in the 12th board final examination. if you want to obtain meritious marks or full marks then you should have good command on concepts that can be developed by practice therefore you should practice NCERT solutions and NCERT exercise solutions.

Also Read

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism - Download PDF

NCERT Books for Class 12 Hindi 2024 - Download chapter wise PDFs here

NCERT Books for Class 12 Biology 2024 - Download Free PDF

NCERT Books for Class 12 Chemistry 2024 - Download Free Pdf

NCERT Book for Class 12 Maths 2024 - Download Free PDF

NCERT Book for Class 12 Physics 2024 - Download Free PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Syllabus for Class 12 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 12 2024 (All Subjects) - Download PDF Here

NCERT Syllabus for Class 6 to 12 (2023-24) - All Subjects PDF Download

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions for Class 12 Maths (Updated 2023-24)

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Certifications By Top Providers

Artificial Intelligence Projects

Via Great Learning

Introduction to Web Development with HTML CSS JavaScript

Via IBM

Introduction to Watson AI

Via IBM

Full-Stack Web Development

Via Masai School

Introduction to Data Science

Via IBM

Digital Banking Business Model

Via State Bank of India

1111 courses

788 courses

327 courses

141 courses

Harvard University, Cambridge

98 courses

IBM

85 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

History

Environmental Studies

Psychology

Data Science

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Lancaster University, Lancaster

Bailrigg, Lancaster LA1 4YW

Top Universities in Australia for International Students 2024 - QS Ranking

11 min ⋆ May 02, 2024 12:05 PM IST

SAT Exam Fees 2024 - Registration, Late, Cancellation, Score Services Fee

4 min ⋆ Mar 11, 2024 07:03 AM IST

SAT Sample Papers 2024 - Question Papers PDF for SAT Practice Test

7 min ⋆ May 02, 2024 11:05 AM IST

Top Universities in Canada for International Students 2024 - QS Ranking

9 min ⋆ May 02, 2024 10:05 AM IST

Study MBBS in USA for Indian and International Students 2024

14 min ⋆ Feb 01, 2024 04:02 AM IST

How to Apply for Eligibility Certificate for Studying MBBS Abroad?

6 min ⋆ May 02, 2024 09:05 AM IST

Related E-books & Sample Papers

CBSE Class 11, 12 Physics Syllabus 2024-25

240+ Downloads

CBSE Class 11, 12 Economics Syllabus 2024-25

87+ Downloads

CBSE Class 11, 12 Sociology Syllabus 2024-25

108+ Downloads

CBSE Class 11, 12 Sanskrit (Elective) Syllabus 2024-25

31+ Downloads

CBSE Class 11, 12 Sanskrit (Core) Syllabus 2024-25

9+ Downloads

CBSE Class 11, 12 Psychology Syllabus 2024-25

35+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer

Sajal Trivedi 29 January,2024

i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer

Upasana Barman 24 August,2022

i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.

As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.

Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.

Believe in Yourself! You can make anything happen

All the very best.

Read Complete Answer

Mayankjha.student2007 23 August,2022

if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer

Nuthalapati Vyshnavi 21 August,2022

I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer

Muskan Dhalwal 17 August,2022

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

300M+
Students
36,000+
Colleges
550+
Exams
1500+
E-Books
16000+
Certifications

We Appeared in

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability

NCERT Continuity And Differentiability Class 12 Questions And Answers

Applications for Admissions are open.

ALLEN NEET Coaching

Aakash iACST Scholarship Test 2024

NCERT Continuity And Differentiability Class 12 Questions And Answers PDF Free Download

Continuity And Differentiability Class 12 NCERT Solutions - Important Formulae

SAT® | CollegeBoard

TOEFL ® Registrations 2024

NCERT Continuity And Differentiability Class 12 Questions And Answers (Intext Questions and Exercise)

Topics of NCERT class 12 maths chapter 5 Continuity and Differentiability

NCERT class 12 maths ch 5 question answer - Topics

NCERT solutions for class 12 maths - Chapter wise

NCERT solutions for class 12 subject wise

NCERT Solutions class wise

NCERT Books and NCERT Syllabus

Tips to Use NCERT Solutions for Class 12 Maths Chapter 5

Frequently Asked Question (FAQs)