-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


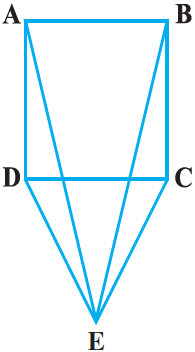
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ADE
BCE.
Answers (2)
Given, that CDE is an equilateral triangle
Then DE = EC = DC
and CDE =
DEC =
ECD = 60°
To prove: ADE
BCE
Proof :
ABCD is a square then,
AB = BC = CD = AD
A =
D =
B =
C = 90°
ADE =
ADC +
CDE = 90° + 60°
and BCE =
BCD +
DCE = 90° + 60°
Then ADE =
BCE
In ADE and
BCE
AD = BC (Given)
DE = EC (Given)
ADE =
BCE (from above)
By SAS criterion of congruence
ADE
BCE
Hence proved.
Given, CDE is an equilateral triangle
Then DE = EC = DC
and CDE =
DEC =
ECD = 60°
To prove : ADE
BCE
Proof :
ABCD is a square then,
AB = BC = CD = AD
A =
D =
B =
C = 90°
ADE =
ADC +
CDE = 90° + 60°
and BCE =
BCD +
DCE = 90° + 60°
Then ADE =
BCE
In ADE and
BCE
AD = BC (Given)
DE = EC (Given)
ADE =
BCE (from above)
By SAS criterion of congruence
ADE
BCE
Hence proved.
Similar Questions
- In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
- 1500 families with 2 children were selected randomly, and the following data were recorded:Compute the probability of a family, chosen at random, having 2 girls
- 1500 families with 2 children were selected randomly, and the following data were recorded: 1 girl

