Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- #1.3
- #8.5
- #Fill in the blanks
- #Match the column
- #Short Answer type
- #Long answer type
- #True-false based type
- #Multiple Choice Questions (MCQs)
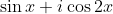 and
and 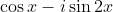 are conjugate to each other for:
are conjugate to each other for:
A. 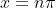
B. 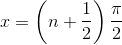
C. 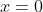
D. No value of x
A.
B.
C.
D. No value of x
Answers (1)
The answer is the option (c).
Comparing the real and imaginary part, we get
The above value is not satisfied by tan x = 1. Hence no value of x is possible.
View full answer
Similar Questions
- 0.3780 g of an organic chloro compound gave 0.5740 g of silver chloride in Carius estimation. Calculate the percentage of chlorine present in the compound.
- 1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.
- At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at – 20 °C ?

