Browse by Stream
-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- #Thermodynamics
- #Physics
- #Medical
- #National Eligibility Cum Entrance Test
- #Class 11
- #National Eligilibility Cum Entrance Test
A mercury manometer consists of two unequal arms of equal cross-section and lengths
. The two open ends are sealed with air in the tube at a pressure of
of mercury. Some amount of mercury is now introduced in the monometer through the stopcock connected to it. If mercury resis in the shorter tube to a length
in steady state, find the length of the mercury column risen in the longer tube.
Option: 1
-
Option: 2
-
Option: 3
-
Option: 4
-
Answers (1)

Let and be the pressures in centimetre of mercury in the two arms after introducing mercury in the tube. Suppose the mercury column rises in the second arm to
.
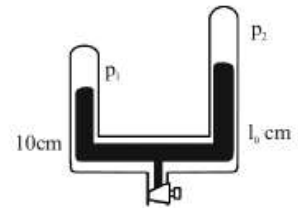
Using constant for the shorter arm,
Using constant for the longer arm,
From the figure,
.
Thus by (i),
.
or
Putting in (ii),
The required length is .
View full answer
NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks


