Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Medical
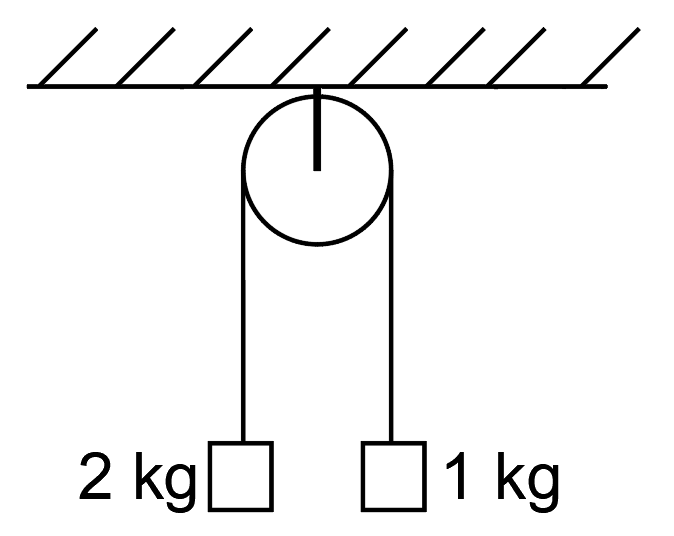
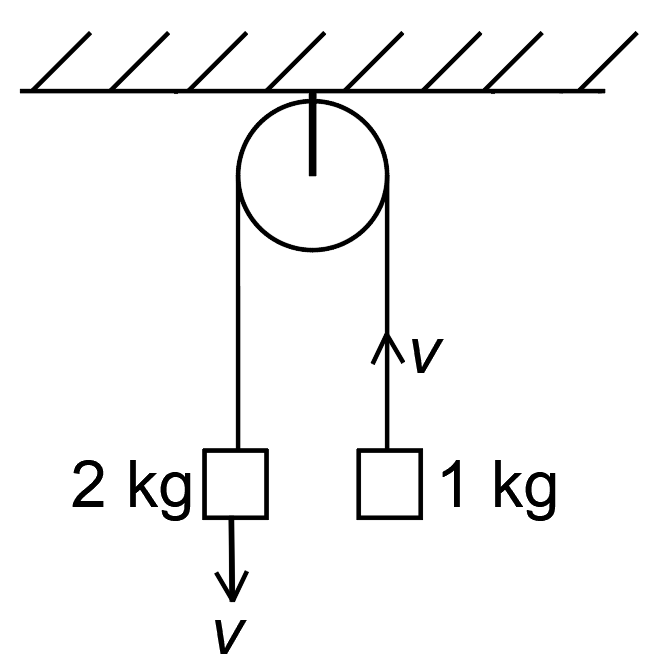
  • A pulley having moment of inertia'  ' conne

A pulley having moment of inertia' 1 \mathrm{~kg}-\mathrm{m}^2 ' connects two blocks of masses 2 \mathrm{~kg} and 1 \mathrm{~kg} respectively as shown in the figure. If the system is released from the rest, find the speed of both masses at t=10 \mathrm{~s}. [Given, g=10 \mathrm{~m} / \mathrm{s}^2 ] \begin{gathered}{[\text { radius of the pulley }} =1 \mathrm{~m} \text { ] }\end{gathered}

Option: 1

5 \mathrm{~m} / \mathrm{s}


Option: 2

10 \mathrm{~m} / \mathrm{s}


Option: 3

15 \mathrm{~m} / \mathrm{s}


Option: 4

25 \mathrm{~m} / \mathrm{s}


Answers (1)

best_answer

Applying angular impulse about the axis of rotation of the pulley.

\begin{aligned} \text { Angular impulse } & =(M-m) g t \\ & =(2-1) \times 10 \times 10 \\ & =100 \end{aligned}

\begin{aligned} \text { Angular impulse } & =\text { change in angular momentum } \\ & =M v r+m v r+I w \\ 100 & =M v r+m v r+I\left(\frac{v}{r}\right) \\ 100 & =2 v+v+\frac{1}{1} \times v \\\end{aligned}

                                \begin{aligned} & 4v=100\\ & v=25 m/s \\\end{aligned}

Posted by

seema garhwal

View full answer

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

Similar Questions

Trending Articles/News

anam-khan

NEET not suitable for BPT, BOT admissions, says TN CM to PM
anam-khan

Failed NEET twice, youth allegedly cuts off his own foot to secure disability quota seat
anam-khan

NMC to speed up NEET counselling with seat-approval calendar, allow for-profits to set up medical colleges

Latest Question