Apply to Aakash iACST Scholarship Test 2024
NCERT Probability Class 10 Solutions Excercise: 15.1
Answer:
Probability of an event E + Probability of the event ‘not E’ = 1
Q1 (ii) The probability of an event that cannot happen is ______. Such an event is called ______.
Answer:
The probability of an event that cannot happen is 0. Such an event is called an impossible event.
When there is no outcome favorable, i.e., the number of outcomes is zero.
Q1 (iii) The probability of an event that is certain to happen is_____ . Such an event is called _______.
Answer:
The probability of an event that is certain to happen is 1. Such an event is called a sure/certain event
When the number of favorable outcomes is the same as the number of all possible outcomes it is a sure event.
Q1 (iv) The sum of the probabilities of all the elementary events of an experiment is _______.
Answer:
The sum of the probabilities of all the elementary events of an experiment is 1 .
Q1 (v) The probability of an event is greater than or equal to and less than or equal to ________ .
Answer:
The probability of an event is greater than or equal to 0 and less than or equal to 1 .
Answer:
It is not an equally likely event since it relies on various factors that are not alike for both the outcomes.
Q2 (ii) Which of the following experiments have equally likely outcomes? Explain.
A player attempts to shoot a basketball. She/he shoots or misses the shot.
Answer:
It is not an equally likely event, because it depends on the ability and amount of practice of the player. If he is a professional player, he will more likely have a successful shot. Whereas an amateur player will more likely miss the shot.
Q2 (iii) Which of the following experiments have equally likely outcomes? Explain.
A trial is made to answer a true-false question. The answer is right or wrong.
Answer:
It is an equally likely event. The only options are true or false and only one of them is correct.
Q2 (iv) Which of the following experiments have equally likely outcomes? Explain.
A baby is born. It is a boy or a girl.
Answer:
It is an equally likely event. The only possibilities of gender are boy and girl. Hence if not boy then girl and vice versa.
Answer:
The tossing of the coin is considered to be a fair way of deciding because the only possible outcomes are head and tails. Hence they are equally likely events.
Q4 Which of the following cannot be the probability of an event?
(A) 2/3
(B) –1.5
(C) 15%
(D) 0.7
Answer:
We know, probability of an event is either greater than or equal to 0 and always less than or equal to 1. Hence the probability of an event can never be negative.
Therefore, (B) cannot be the probability of an event.
Also, (A) :
(C):
(D): 0.7
Hence (A), (C), (D) all lie between 0 and 1.
Q5 If P(E) = 0.05, what is the probability of ‘not E’?
Answer:
Given,
We know,
Hence, the probability of 'not E' is 0.95
Answer:
According to the question, the bag contains only lemon-flavored candies. It does not contain any orange flavor candy. Hence, every time only lemon flavor candy will come out. Therefore, i.e. event of taking out an orange-flavored candy is an impossible event.
Answer:
According to the question, the bag contains only lemon-flavored candies. So the event that Malini takes out a lemon-flavored candy is a sure event. Therefore,
Answer:
Given,
Probability of two students not having the same birthday
Probability of two students having the same birthday =
Hence, the probability that the 2 students have the same birthday is 0.008
Answer:
Total number of balls in the bag = 8
No. of red balls = 3
No. of black balls = 5
(i) Let E be the event of getting a red ball
n(E) = No. of red balls = 3
n(S) = No. of total balls = 8
Probability of the ball drawn to be red =
Answer:
Total number of balls in the bag = 8
No. of red balls = 3
No. of black balls = 5
(ii) We know,
where are complementary events.
Probability of not getting the red ball
Answer:
Given,
Total number of balls in the bag = 5 + 8 + 4 = 17
(i) Let R be the event that the ball taken out is red
The number of possible outcomes = 17
The number of outcomes favorable to the event R = 5
Answer:
Given,
Total number of balls in the bag = 5 + 8 + 4 = 17
(ii) Let W be the event that the ball taken out is white
The number of possible outcomes = 17
The number of outcomes favorable to the event W = 8
Answer:
Given,
Total number of balls in the bag = 5 + 8 + 4 = 17
(iii) Let G be the event that the ball taken out is green
The number of possible outcomes = 17
The number of outcomes favorable to the event G = 4
The required probability of not getting a green ball is
Answer:
Total number of coins in the piggy bank = 100+50+20+10 = 180
Let E be the event of getting a 50p coin.
Number of possible outcomes = 180
Number of outcomes favorable to event E = 100
Therefore, the probability of getting a 50p coin is
Answer:
Total number of coins in the piggy bank = 100+50+20+10 = 180
Let F be the event of getting an Rs. 5 coin.
Number of possible outcomes = 180
Number of outcomes favorable to event E = 10
Therefore, the probability of not getting an Rs. 5 coin is

Answer:
Total number of fishes in the tank = 5 (male) + 8 (female) = 13
Let E be the event that the fish taken out is a male fish.
Number of possible outcomes = 13
Number of outcomes favorable to E = 5
Therefore, the probability that the fish are taken out is a male fish is
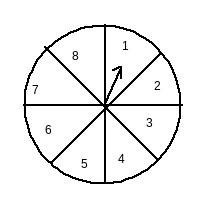
Answer:
Total posible outcomes = {1,2,3,4,5,6,7,8}
Number of possible outcomes = 8
Let E be the event of getting 8.
Therefore, the probability that it will point at 8 is
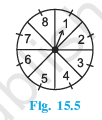
Answer:
Total posible outcomes = {1,2,3,4,5,6,7,8}
Number of possible outcomes = 8
Let E be the event of pointing at an odd number.
Total number of odd numbers = n({1,3,5,7}) = 4
Therefore, the probability of getting an odd number is
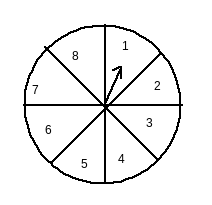
Answer:
Total posible outcomes = {1,2,3,4,5,6,7,8}
Number of possible outcomes = 8
Let E be the event of pointing at number greater than 2
Number of favouable outcomes= n({3,4,5,6,7}) = 5
Therefore, the probability of pointing at a number greater than 2 is
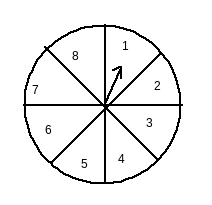
Answer:
Total possible outcomes = {1,2,3,4,5,6,7,8}
Number of possible outcomes = 8
Let E be the event of pointing at a number less than 9
Since all the numbers on the wheel are less than 9, this is the sure event.
Number of favorable outcomes = 8
Therefore, the probability of pointing at a number less than 9 is .
Q13 (i) A die is thrown once. Find the probability of getting a prime number
Answer:
Possible outcomes when a die is thrown = {1,2,3,4,5,6}
Number of possible outcomes once = 6
(i) Let E be the event of getting a prime number.
Prime numbers on the die are = {2,3,5}
Number of favorable outcomes = 3
Therefore, the probability of getting a prime number is
Q13 (ii) A die is thrown once. Find the probability of getting a number lying between 2 and 6
Answer:
Possible outcomes when a die is thrown once = {1,2,3,4,5,6}
Number of possible outcomes = 6
(ii) Let F be the event of getting a number lying between 2 and 6
Numbers lying between 2 and 6 on the die are = {3,4,5}
Number of favorable outcomes = 3
Therefore, the probability of getting a number lying between 2 and 6 is
Q13 (iii) A die is thrown once. Find the probability of getting an odd number.
Answer:
Possible outcomes when a die is thrown = {1,2,3,4,5,6}
Number of possible outcomes once = 6
(iii) Let O be the event of getting an odd number.
Odd numbers on the die are = {1,3,5}
Number of favorable outcomes = 3
Therefore, the probability of getting an odd number is .
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(1) Let E be the event of getting a king of red color.
There are only red color kings: Hearts and diamonds
Hence, number of favorable outcomes = 2
Therefore, the probability of getting a king of red color is
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(2) Let E be the event of getting a face card.
Face cards: (J, Q, K) of each four suits
Hence, number of favorable outcomes = 12
Therefore, the probability of getting a face card is
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(3) Let E be the event of getting a red face card.
Face cards: (J, Q, K) of hearts and diamonds
Hence, number of favourable outcomes = 3x2 = 6
Therefore, the probability of getting a red face card is
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(4) Let E be the event of getting the jack of hearts
Hence, the number of favourable outcomes = 1
Therefore, the probability of getting the jack of hearts is
14 (v) One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting (v)a spade
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(5) Let E be the event of getting a spade.
There are 13 cards in each suit. {2,3,4,5,6,7,8,9,10,J,Q,K,A}
Hence, number of favourable outcomes = 13
Therefore, the probability of getting a spade is
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, total possible outcomes = 52
(6) Let E be the event of getting the queen of diamonds
Hence, the number of favorable outcomes = 1
Therefore, the probability of getting the queen of diamonds is
Answer:
Total number of cards = 5
Hence, the total possible outcomes = 5
(1) There is only one queen.
Hence, favorable outcome = 1
Answer:
When the queen is kept aside, there are only 4 cards left
Hence, the total possible outcomes = 4
(2a) There is only one ace.
Hence, favorable outcome = 1
Therefore, the probability of getting an ace is 0.25
Answer:
When the queen is kept aside, there are only 4 cards left
Hence, the total possible outcomes = 4
(2b) Since there is no queen left.
Hence, favorable outcome = 0
Therefore, the probability of getting a queen is 0. Thus, it is an impossible event.
Answer:
Total number of pens = 132(good) + 12(defective)
Hence, the total possible outcomes = 144
Number of good pens = number of favorable outcomes = 132
Answer:
Total number of bulbs = 20
Hence, total possible outcomes = 20
Number of defective bulbs = 4
Hence, the number of favorable outcomes = 4
Answer:
Total number of bulbs = 20
Hence, total possible outcomes = 20
Number of defective bulbs = 4
Hence, the number of favorable outcomes = 4
Answer:
Total number of discs = 90
Number of discs having a two-digit number between 1 and 90 = 81
Answer:
Total number of discs = 90
Perfect square numbers between 1 and 90 are {1, 4, 9, 16, 25, 36, 49, 64, 81}
Therefore, the total number of discs having perfect squares = 9.
Answer:
Total number of discs = 90
Numbers between 1 and 90 that are divisible by 5 are {5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90}
Therefore, total number of discs having numbers that are divisible by 5 = 18.
Q19 (i) A child has a die whose six faces show the letters as given below:
The die is thrown once. What is the probability of getting (i) A?
Answer:
The six faces of the die contains : {A,B,C,D,E,A}
Total number of letters = 6
(i) Since there are two A's,
number of favorable outcomes = 2
Therefore, the probability of getting A is
Q19 (ii) A child has a die whose six faces show the letters as given below:
The die is thrown once. What is the probability of getting (ii) D?
Answer:
The six faces of the die contains : {A,B,C,D,E,A}
Total number of letters = 6
(i) Since there is only one D,
number of favorable outcomes = 1
Therefore, the probability of getting D is
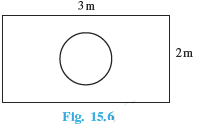
Answer:
Here, the Total outcome in the area of the rectangle and favorable outcome is the area of the circle.
Area of the rectangle =
Area of the circle =
Answer:
Total number of pens = 144
Total number of defective pens = 20
Number of good pens = 144-20 = 124
She will buy it if the pen is good.
Therefore, the probability that she buys = probability that the pen is good =
Answer:
Total number of pens = 144
Total number of defective pens = 20
She will buy it if the pen is good.
Therefore, the probability that she will not buy = probability that the pen is defective =
Q22 (i) Refer to Example 13. (i) Complete the following table:
Event: 'sum on 2 dice' | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1/36 | 5/36 | 1/36 |
Answer:
The table becomes:
| The sum of two dice | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 |
Answer:
A student argues that "there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability of 1/11. We do not agree with this argument because there are a different number of possible outcomes for each sum. we can see that each sum has a different probability.
Answer:
The possible outcomes when a coin is tossed 3 times: (Same as 3 coins tossed at once!)
{HHH, HHT, HTH, HTT, THH, TTH, THT, TTT}
Number of total possible outcomes = 8
For Hanif to win, there are only two favorable outcomes: {HHH, TTT}
Number of favorable outcomes = 2
Therefore, the probability that Hanif will lose is
Q24 (i) A die is thrown twice. What is the probability that 5 will not come up either time?
Answer:
When a die is thrown twice, the possible outcomes =
Total number of possible outcomes =
The outcomes when 5 comes up either on them =
{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}
Number of such favorable outcomes = 11
Therefore, the probability that 5 will not come either time is
24 (ii) A die is thrown twice. What is the probability that 5 will come up at least once?
Answer:
When a die is thrown twice, the possible outcomes =
Total number of possible outcomes =
The outcomes when 5 comes up at least once =
{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}
Number of such favorable outcomes = 11
Therefore, the probability that 5 comes at least once is
Answer:
The possible outcomes when two coins are tossed = {HH, HT, TH, TT}
Total number of possible outcomes = 4
Hence, the given statement is not correct. This is because one of each can occur in two different ways. Hence the mentioned events are not equally likely.
Answer:
The possible outcomes when a die is thrown= {1,2,3,4,5,6}
Total number of possible outcomes = 6
Number of odd number, {1,3,5} = 3
And, number of even numbers {2,4,6} = 3
Hence, both these events are equally likely
NCERT Probability Class 10 Solutions Excercise: 15.2
Answer:
Total possible ways Shyam and Ekta can visit the shop =
(1) A case that both will visit the same day.
Shyam can go on any day between Tuesday to Saturday in 5 ways.
For any day that Shyam goes, Ekta will go on the same day in 1 way.
Total ways that they both go in the same day =
Answer:
Total possible ways Shyam and Ekta can visit the shop =
(2) The case that both will visit the shop on consecutive days.
Shyam can go on any day between Tuesday to Friday in 4 ways.
For any day that Shyam goes, Ekta will go on the next day in 1 way
Similarly, Ekta can go on any day between Tuesday to Friday in 4 ways.
And Shyam will go on the next day in 1 way.
(Note: None of the cases repeats since they are in a different order!)
Total ways that they both go in the same day =
Answer:
Total possible ways Shyam and Ekta can visit the shop =
(1) A case that both will visit the same day.
Shyam can go on any day between Tuesday to Saturday in 5 ways.
For any day that Shyam goes, Ekta will go on a different day in ways.
Total ways that they both go in the same day =
 What is the probability that the total score is (i) even?
What is the probability that the total score is (i) even?
Answer:
| + | 1 | 2 | 2 | 3 | 3 | 6 |
| 1 | 2 | 3 | 3 | 4 | 4 | 7 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 12 |
Total possible outcomes when two dice are thrown =
(1) Number of times when the sum is even = 18
 What is the probability that the total score is (ii) 6?
What is the probability that the total score is (ii) 6?
Answer:
| + | 1 | 2 | 2 | 3 | 3 | 6 |
| 1 | 2 | 3 | 3 | 4 | 4 | 7 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 12 |
Total possible outcomes when two dice are thrown =
Number of times when the sum is 6 = 4
 What is the probability that the total score is (iii) at least 6?
What is the probability that the total score is (iii) at least 6?
Answer:
| + | 1 | 2 | 2 | 3 | 3 | 6 |
| 1 | 2 | 3 | 3 | 4 | 4 | 7 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 12 |
Total possible outcomes when two dice are thrown =
Number of times when the sum is at least 6, which means sum is greater than 5 = 15
Answer:
Let there be the number of blue balls in the bag.
Number of red balls = 5
Thus, the total number of balls = total possible outcomes =
And,
According to question,
Therefore, there are 10 blue balls in the bag.
Answer:
Total number of balls in the bag = 12
Number of black balls in the bag =
According to the question,
6 more black balls are added to the bag.
Total number of balls =
And, the new number of black balls =
Also,
The required value of is 3
Answer:
Let be the number of blue marbles in the jar.
Number of green marbles in the jar =
According to question,
Number of blue marbles in the jar is 8









