-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


- #1.3
- #8.6
- #Fill in the blanks
- #Short Answer type
- #Long answer type
- #True-false based type
- #Multiple Choice Questions (MCQs)
Q: Find the unit vector in the direction of sum of vectors 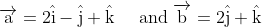
Answers (1)
Solution
We have,
$$
\begin{aligned}
& \overrightarrow{\mathrm{a}}=2 \hat{\mathrm{i}}-\hat{\mathrm{\jmath}}+\hat{\mathrm{k}} \\
& \overrightarrow{\mathrm{~b}}=2 \hat{\mathrm{\jmath}}+\hat{\mathrm{k}}
\end{aligned}
$$
Since, unit vector is needed to be found in the direction of the sum of vectors $\vec{a}$ and $\vec{b}$.
So, add vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$.
Let, $\vec{c}=\vec{a}+\vec{b}$
Substituting the values of vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$.
$$
\begin{aligned}
& \Rightarrow \vec{c}=(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})+(2 \hat{\jmath}+\hat{\mathrm{k}}) \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}}+2 \hat{\jmath}+\hat{\mathrm{k}} \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}-\hat{\jmath}+2 \hat{\jmath}+\mathrm{k}+\hat{\mathrm{k}} \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}
\end{aligned}
$$
We know that a unit vector in a normed vector space is a vector (often a spatial vector) of length 1.
To find a unit vector with the same direction as a given vector, we divide by the magnitude of the vector.
For finding unit vector, we have the formula:
$$
\hat{c}=\frac{\overrightarrow{\mathrm{c}}}{|\overrightarrow{\mathrm{c}}|}
$$
Substitute the value of $\vec{c}$.
$$
\Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{k}}{|2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}}|}
$$
Here, $|2 \hat{\imath}+\hat{\jmath}+2 \hat{k}|=\sqrt{2^2+1^2+2^2}$
$$
\begin{aligned}
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{2^2+1^2+2^2}} \\
& \Rightarrow \hat{\mathrm{c}}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{4+1+4}} \\
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{9}} \\
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{3}
\end{aligned}
$$
Thus, unit vector in the direction of sum of vectors $\vec{a}$ and $\vec{b}$ is $\frac{2 \hat{i}+\hat{j}+2 \hat{k}}{3}$.
Similar Questions
- 100 g of liquid A (molar mass 140 g mol^-1) was dissolved in 1000 g of liquid B (molar mass 180 g mol^-1).The vapour pressure of pure liquid B was found to be 500 torr.
- 100 turn rectangular coil ABCD (in X-Y plane) is hung from one arm of a balance (shown in figure). A mass 500 g is added to the other arm to balance the weight of the coil.
- 100m long antenna is mounted on a 500m tall building The complex can become a transmission tower for waves with λ (a) ~ 400 m (b) ~ 25 m (c) ~ 150 m (d) ~ 2400 m

