Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Medical
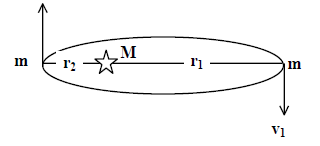
  • A planet of mass moves along an ellipse around the sun so that its maximum and minimum distance from the sun is equal to <img alt="\mat

A planet of mass \mathrm{m} moves along an ellipse around the sun so that its maximum and minimum distance from the sun is equal to \mathrm{r_1 \: and \: r_2} respectively. Then the angular momentum of this plane relative to the centre of the sun.
 

Option: 1

\mathrm{m \sqrt{\frac{2 G M r_1 r_2}{r_1+r_2}}}

 


Option: 2

\mathrm{\mathrm{m} \sqrt{\frac{3 \mathrm{GM} \mathrm{r_1} \mathrm{r}_2}{\mathrm{r}_1+\mathrm{r}_2}}}
 


Option: 3

\mathrm{m \sqrt{\frac{\mathrm{GM} \mathrm{r_1} r_2}{\mathrm{r}_1+\mathrm{r}_2}}}
 


Option: 4

\mathrm{\mathrm{m} \sqrt{\frac{\mathrm{GM} \mathrm{r}_1 \mathrm{r}_2}{2\left(\mathrm{r}_1+\mathrm{r}_2\right)}}}


Answers (1)

best_answer

The angular momentum

=\mathrm{L}=\mathrm{mv}_1 \mathrm{r}_1                   .............(1)

Conservation of angular momenta at 1 and 2 ;

\mathrm{mv}_1 \mathrm{r}_1=\mathrm{mv}_2 \mathrm{r}_2

\Rightarrow \mathrm{v}_1 \mathrm{r}_1=\mathrm{v}_2 \mathrm{r}_2             ..............(2)

Conservation of energy at 1 and 2;

\mathrm{ \frac{1}{2} m v_1^2-\frac{G M m}{r_1} }

\mathrm{ = \frac{1}{2} m v_2^2-\frac{G M m}{r_2} }      ......(3)

Using (2) and (3) we obtain

\mathrm{ v_1=\sqrt{2 G M\left(\frac{1}{r_1}-\frac{1}{r_2}\right)+v_2^2} }

\mathrm{ V_1=\sqrt{2 G M\left(\frac{1}{r_1}-\frac{1}{r_2}\right)+\left(\frac{v_1 r_1}{r_2}\right)^2} }

\mathrm{ \Rightarrow v_1^2\left[1-\left(\frac{r_1}{r_2}\right)^2\right]=2 G M\left(\frac{r_2-r_1}{r_1 r_2}\right) }

\mathrm{ \Rightarrow V_1=\sqrt{\frac{2 G M r_2}{r_1\left(r_1+r_2\right)}} }

\mathrm{ \therefore L=m v_1 r_1=m \sqrt{\frac{2 G M r_1 r_2}{r_1+r_2}} }

Hence option 1 is correct.




 




 

Posted by

Rakesh

View full answer

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

Similar Questions

Trending Articles/News

anam-khan

Karnataka AYUSH UG 2025: Round 3 stray vacancy registration begins; option entry ends in two days
anam-khan

Maharashtra NEET UG 2025: Just 114 marks enough for private MBBS seat; govt colleges close at 500
anam-khan

UP NEET AYUSH 2025: Stray vacancy round 3 schedule out; registration ends in two days

Latest Question