NCERT solutions for Class 12 Maths Chapter 4 Determinants 2021

NCERT solutions for Class 12 Maths Chapter 4 Determinants

Edited By Ramraj Saini | Updated on Sep 13, 2023 09:18 PM IST | #CBSE Class 12th

NCERT Determinants Class 12 Questions And Answers

NCERT solutions for Class 12 Maths Chapter 4 Determinants are proved here. These NCERT solutions are created by expert team at Careers360 keeping align the latest syllabus of CBSE 2023-24. In this chapter, students will be able to understand the Class 12 Maths Chapter 4 NCERT solutions. If you multiply a matrix with the coordinates of a point, it will give a new point in the space which is explained in NCERT class 12 chapter 4 maths Determinants solutions. In this sense, the matrix is a linear transformation. The determinant of the matrix is the factor by which its volume blows up. You will be familiar with these points after going through ch 4 maths class 12. Interested students can visit chapter wise NCERT solution for math.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Determinants Class 12 Questions And Answers
NCERT Determinants Class 12 Questions And Answers PDF Free Download
NCERT Class 12 Maths Chapter 4 Question Answer - Important Formulae
NCERT Class 12 Maths Chapter 4 Question Answer (Intext Questions and Exercise)
NCERT determinants class 12 solutions: Excercise: 4.5
NCERT solutions for class 12 Maths - Chapter wise
NCERT solutions for class 12 - subject wise
NCERT Solutions - Class Wise
NCERT Books and NCERT Syllabus

NCERT solutions for Class 12 Maths Chapter 4 Determinants

The important topics of class 12 maths ch 4 are determinants and their properties, finding the area of the triangle, minor and cofactors, adjoint and the inverse of the matrix, and applications of determinants like solving the system of linear equations, etc are covered in NCERT solutions for Class 12 Maths Chapter 4 Determinants. If you are looking for determinants class 12 solutions then check all NCERT solutions at a single place which will help the students to learn CBSE maths. Here you will get NCERT solutions for class 12 also. Read further to know more about NCERT solutions for Class 12 Maths Chapter 4 PDF download.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.

Apply Now

Also read:

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

NCERT Determinants Class 12 Questions And Answers PDF Free Download

Download PDF

NCERT Class 12 Maths Chapter 4 Question Answer - Important Formulae

>> Determinant of a Matrix: The determinant is the numerical value of a square matrix.

For a square matrix A of order n, the determinant is denoted by det A or |A|.

Minor and Cofactor of a Matrix:

Minor of an element aij of a determinant is a determinant obtained by deleting the ith row and jth column in which element aij lies.

The cofactor of an element aij of a determinant, denoted by A_ij or C_ij, is defined as A_ij = (-1)(i+j) * M_ij, where M_ij is the minor of element a_ij.

Value of a Determinant (2x2 and 3x3 matrices):

For a 2x2 matrix A: |A| = a₁₁ * a₂₂ - a₂₁* a₁₂

For a 3x3 matrix A: |A| = a₁₁ * |A₁₁| - a₁₂ * |A₁₂| + a₁₃ * |A₁₃|

Singular and Non-Singular Matrix:

If the determinant of a square matrix is zero, the matrix is said to be singular; otherwise, it is non-singular.

Determinant Theorems:

If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.

The determinant of the product of matrices is equal to the product of their respective determinants, i.e., |AB| = |A| * |B|.

Adjoint of a Matrix:

The adjoint of a square matrix A is the transpose of the matrix obtained by cofactors of each element of the determinant corresponding to A. It is denoted by adj(A).

In general, the adjoint of a matrix A = [a_ij]_n×n is a matrix [A_ji]_n×n, where A_ji is a cofactor of element a_ji.

Properties of Adjoint of a Matrix:

A(adj A) = (adj A)A = |A|In (Identity Matrix)

|adj A| = |A|(n-1)

adj(AT) = (adj A)T (Transpose of the adjoint)

Finding Area of a Triangle Using Determinants:

The area of a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) is given by

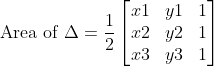
1694619308727

Inverse of a Square Matrix:

For a non-singular matrix A (|A| ≠ 0), the inverse A-1 is defined as A^-1 = (1/|A|) * adj(A).

Properties of an Inverse Matrix:

(A^-1)^-1 = A

(AT)^-1 = (A^-1)T

(AB)^-1 = B^-1A^-1

(ABC)^-1 = C^-1B^-1A^-1

adj(A^-1) = (adj A)^-1

Solving a System of Linear Equations using Inverse of a Matrix:

Given a system of equations AX = B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

Case I: If |A| ≠ 0, the system is consistent, and X = A^-1B has a unique solution.

Case II: If |A| = 0 and (adj A)B ≠ 0, the system is inconsistent and has no solution.

Case III: If |A| = 0 and (adj A)B = 0, the system may be either consistent or inconsistent, depending on whether it has infinitely many solutions or no solutions.

Free download Class 12 Determinants NCERT Solutions for CBSE Exam.

NCERT Class 12 Maths Chapter 4 Question Answer (Intext Questions and Exercise)

NCERT determinants class 12 questions and answers: Excercise- 4.1

Question:1 Evaluate the following determinant- $\begin{vmatrix} 2 & 4\\ -5 & -1\end{vmatrix}$

Answer:

The determinant is evaluated as follows

$\begin{vmatrix} 2 & 4\\ -5 & -1\end{vmatrix} = 2(-1) - 4(-5) = -2 + 20 = 18$

Question:2(i) Evaluate the following determinant- $\begin{vmatrix} \cos \theta & -\sin \theta \\ \sin \theta &\cos \theta \end{vmatrix}$

Answer:

The given two by two determinant is calculated as follows

$\dpi{100} \begin{vmatrix} \cos \theta & -\sin \theta \\ \sin \theta &\cos \theta \end{vmatrix} = cos \theta (\cos \theta) - (-\sin \theta)\sin \theta = \cos^2\theta + \sin ^2 \theta = 1$

Question:2(ii) Evaluate the following determinant- $\begin{vmatrix}x^2-x+1 & x-1\\x+1 &x+1 \end{vmatrix}$

Answer:

We have determinant $\begin{vmatrix}x^2-x+1 & x-1\\x+1 &x+1 \end{vmatrix}$

So, $\dpi{100} \begin{vmatrix}x^2-x+1 & x-1\\x+1 &x+1 \end{vmatrix} = (x^2-x+1)(x+1) - (x-1)(x+1)$

$= (x+1)(x^2-x+1-x+1) = (x+1)(x^2-2x+2)$

$=x^3-2x^2+2x +x^2-2x+2$

$= x^3-x^2+2$

Question:3 If $A = \begin{bmatrix} 1 & 2\\ 4 &2 \end{bmatrix}$ , then show that $| 2 A |=4|A|$

Answer:

Given determinant $A = \begin{bmatrix} 1 & 2\\ 4 &2 \end{bmatrix}$ then we have to show that $| 2 A |=4|A|$ ,

So, $A = \begin{bmatrix} 1 & 2\\ 4 &2 \end{bmatrix}$ then, $2A =2 \begin{bmatrix} 1 & 2\\ 4 &2 \end{bmatrix} = \begin{bmatrix} 2 & 4\\ 8 &4 \end{bmatrix}$

Hence we have $\left | 2A \right | = \begin{vmatrix} 2 &4 \\ 8& 4 \end{vmatrix} = 2(4) - 4(8) = -24$

So, L.H.S. = |2A| = -24

then calculating R.H.S. $4\left | A \right |$

We have,

$\left | A \right | = \begin{vmatrix} 1 &2 \\ 4& 2 \end{vmatrix} = 1(2) - 2(4) = -6$

hence R.H.S becomes $4\left | A \right | = 4\times(-6) = -24$

Therefore L.H.S. =R.H.S.

Hence proved.

Question:4 If $A =\begin{bmatrix} 1 &0 &1 \\ 0& 1& 2\\ 0& 0 &4 \end{bmatrix}$ then show that $|3A|=27|A|$

Answer:

Given Matrix $A =\begin{bmatrix} 1 &0 &1 \\ 0& 1& 2\\ 0& 0 &4 \end{bmatrix}$

Calculating $3A =3\begin{bmatrix} 1 &0 &1 \\ 0& 1& 2\\ 0& 0 &4 \end{bmatrix} = \begin{bmatrix} 3 &0 &3 \\ 0& 3& 6\\ 0& 0 &12 \end{bmatrix}$

So, $\left | 3A \right | = 3(3(12) - 6(0) ) - 0(0(12)-0(6)) + 3(0-0) = 3(36) = 108$

calculating $27|A|$ ,

$|A| = \begin{vmatrix} 1 & 0 &1 \\ 0 & 1 & 2\\ 0& 0 &4 \end{vmatrix} = 1\begin{vmatrix} 1 &2 \\ 0 & 4 \end{vmatrix} - 0\begin{vmatrix} 0 &2 \\ 0& 4 \end{vmatrix} + 1\begin{vmatrix} 0 &1 \\ 0& 0 \end{vmatrix} = 4 -0 + 0 = 4$

So, $27|A| = 27(4) = 108$

Therefore $|3A|=27|A|$ .

Hence proved.

Question:5(i) Evaluate the determinants.

$\begin{vmatrix}3 &-1 &-2 \\0 &0 &-1 \\3 &-5 & 0 \end{vmatrix}$

Answer:

Given the determinant $\begin{vmatrix}3 &-1 &-2 \\0 &0 &-1 \\3 &-5 & 0 \end{vmatrix}$ ;

now, calculating its determinant value,

$\begin{vmatrix}3 &-1 &-2 \\0 &0 &-1 \\3 &-5 & 0 \end{vmatrix} = 3\begin{vmatrix} 0 &-1 \\ -5& 0 \end{vmatrix} -(-1)\begin{vmatrix} 0 &-1 \\ 3& 0 \end{vmatrix} +(-2)\begin{vmatrix} 0 &0 \\ 3& -5 \end{vmatrix}$

$= 3(0-5)+1(0+3) -2(0-0) = -15+3-0 = -12$ .

Question:5(ii) Evaluate the determinants.

$\begin{vmatrix}3 &-4 &5 \\1 &1 &-2 \\2 &3 &1 \end{vmatrix}$

Answer:

Given determinant $\begin{vmatrix}3 &-4 &5 \\1 &1 &-2 \\2 &3 &1 \end{vmatrix}$ ;

Now calculating the determinant value;

$\begin{vmatrix}3 &-4 &5 \\1 &1 &-2 \\2 &3 &1 \end{vmatrix} = 3\begin{vmatrix} 1 &-2 \\ 3&1 \end{vmatrix} -(-4)\begin{vmatrix} 1 &-2 \\ 2& 1 \end{vmatrix}+5\begin{vmatrix} 1 & 1\\ 2& 3 \end{vmatrix}$

$= 3(1+6) +4(1+4) +5(3-2) = 21+20+5 = 46$ .

Question:5(iii) Evaluate the determinants.

$\begin{vmatrix}0 & 1 & 2\\-1 &0 &-3 \\ -2 &3 &0 \end{vmatrix}$

Answer:

Given determinant $\begin{vmatrix}0 & 1 & 2\\-1 &0 &-3 \\ -2 &3 &0 \end{vmatrix}$ ;

Now calculating the determinant value;

$\begin{vmatrix}0 & 1 & 2\\-1 &0 &-3 \\ -2 &3 &0 \end{vmatrix} = 0\begin{vmatrix} 0 &-1 \\ 3& 0 \end{vmatrix} -1\begin{vmatrix} -1 &-3 \\ -2& 0 \end{vmatrix}+2\begin{vmatrix} -1 &0 \\ -2& 3 \end{vmatrix}$

$= 0 - 1(0-6)+2(-3-0) = 6 -6 =0$

Question:5(iv) Evaluate the determinants.

$\begin{vmatrix}2 &-1 &2 \\0 &2 &-1 \\3 &-5 &0 \end{vmatrix}$

Answer:

Given determinant: $\begin{vmatrix}2 &-1 &-2 \\0 &2 &-1 \\3 &-5 &0 \end{vmatrix}$ ,

We now calculate determinant value:

$\begin{vmatrix}2 &-1 &-2 \\0 &2 &-1 \\3 &-5 &0 \end{vmatrix} =2\begin{vmatrix} 2 &-1 \\ -5 & 0 \end{vmatrix} -(-1)\begin{vmatrix} 0 &-1 \\ 3 & 0 \end{vmatrix}+(-2)\begin{vmatrix} 0 &2 \\ 3&-5 \end{vmatrix}$

$=2(0-5)+1(0+3)-2(0-6) = -10+3+12 = 5$

Question:6 If $A=\begin{bmatrix}1 & 1 & -2\\ 2& 1 &-3 \\5 &4 &-9 \end{bmatrix}$ , then find $|A|$ .

Answer:

Given the matrix $A=\begin{bmatrix}1 & 1 & -2\\ 2& 1 &-3 \\5 &4 &-9 \end{bmatrix}$ then,

Finding the determinant value of A;

$|A| = 1\begin{vmatrix} 1 &-3 \\ 4& -9 \end{vmatrix} -1\begin{vmatrix} 2 &-3 \\ 5& -9 \end{vmatrix}-2\begin{vmatrix} 2 &1 \\ 5& 4 \end{vmatrix}$

$= 1(-9+12)-1(-18+15)-2(8-5) =3+3-6 =0$

Question:7(i) Find values of x, if

$\begin{vmatrix}2 &4 \\5 &1 \end{vmatrix} =\begin{vmatrix}2x &4 \\6 &x \end{vmatrix}$

Answer:

Given that $\begin{vmatrix}2 &4 \\5 &1 \end{vmatrix} =\begin{vmatrix}2x &4 \\6 &x \end{vmatrix}$

First, we solve the determinant value of L.H.S. and equate it to the determinant value of R.H.S.,

$\dpi{100} \begin{vmatrix}2 &4 \\5 &1 \end{vmatrix} =2-20 = -18$ and $\begin{vmatrix}2x &4 \\6 &x \end{vmatrix} = 2x(x)-24 = 2x^2-24$

So, we have then,

$-18= 2x^2-24$ or $3= x^2$ or $x= \pm \sqrt{3}$

Question:7(ii) Find values of x, if

$\begin{vmatrix}2 &3 \\ 4 &5 \end{vmatrix}=\begin{vmatrix}x &3 \\2x &5 \end{vmatrix}$

Answer:

Given $\begin{vmatrix}2 &3 \\ 4 &5 \end{vmatrix}=\begin{vmatrix}x &3 \\2x &5 \end{vmatrix}$ ;

So, we here equate both sides after calculating each side's determinant values.

L.H.S. determinant value;

$\dpi{100} \begin{vmatrix}2 &3 \\ 4 &5 \end{vmatrix}= 10 - 12 = -2$

Similarly R.H.S. determinant value;

$\begin{vmatrix}x &3 \\2x &5 \end{vmatrix} = 5(x) - 3(2x) = 5x - 6x =-x$

So, we have then;

$-2 = -x$ or $x =2$ .

Question:8 If $\begin{vmatrix}x &2 \\18 &x \end{vmatrix}=\begin{vmatrix} 6 &2 \\ 18 &6 \end{vmatrix}$ , then $x$ is equal to

(A) $6$ (B) $\pm 6$ (C) $-6$ (D) $0$

Answer:

Solving the L.H.S. determinant ;

$\dpi{100} \begin{vmatrix}x &2 \\18 &x \end{vmatrix}= x^2 - 36$

and solving R.H.S determinant;

$\begin{vmatrix} 6 &2 \\ 18 &6 \end{vmatrix} = 36-36 = 0$

So equating both sides;

$x^2 - 36 =0$ or $x^2 = 36$ or $x = \pm 6$

Hence answer is (B).

NCERT determinants class 12 questions and answers: Excercise - 4.2

Question:1 Using the property of determinants and without expanding, prove that

$\begin{vmatrix}x &a &x+a \\y &b &y+b \\z &c &z+c \end{vmatrix}=0$

Answer:

We can split it in manner like;

$\begin{vmatrix}x &a &x+a \\y &b &y+b \\z &c &z+c \end{vmatrix}= \begin{vmatrix} x &a &x \\ y & b &y \\ z &c &z \end{vmatrix} + \begin{vmatrix} x &a & a\\ y &b &b \\ z&c & c \end{vmatrix}$

So, we know the identity that If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then the value of the determinant is zero.

Clearly, expanded determinants have identical columns.

$\therefore 0 + 0 = 0$

Hence the sum is zero.

Question: 2 Using the property of determinants and without expanding, prove that

$\begin{vmatrix}a-b &b-c &c-a \\b-c &c-a &a-b \\c-a &a-b &b-c \end{vmatrix}=0$

Answer:

Given determinant $\triangle =\begin{vmatrix}a-b &b-c &c-a \\b-c &c-a &a-b \\c-a &a-b &b-c \end{vmatrix}=0$

Applying the rows addition $R_{1} \rightarrow R_{1}+R_{2}$ then we have;

$\triangle =\begin{vmatrix}a-c &b-a &c-b \\b-c &c-a &a-b \\-(a-c) &-(b-a) &-(c-b) \end{vmatrix}=0$

$=-\begin{vmatrix}a-c &b-a &c-b \\b-c &c-a &a-b \\(a-c) &(b-a) &(c-b) \end{vmatrix}=0$

So, we have two rows $R_{1}$ and $R_{2}$ identical hence we can say that the value of determinant = 0

Therefore $\triangle = 0$ .

Question:3 Using the property of determinants and without expanding, prove that

$\begin{vmatrix}2 & 7 &65 \\3 &8 &75 \\5 &9 &86 \end{vmatrix}=0$

Answer:

Given determinant $\dpi{100} \begin{vmatrix}2 & 7 &65 \\3 &8 &75 \\5 &9 &86 \end{vmatrix}$

So, we can split it in two addition determinants:

$\begin{vmatrix}2 & 7 &65 \\3 &8 &75 \\5 &9 &86 \end{vmatrix} = \begin{vmatrix} 2 &7 &63+2 \\ 3& 8 &72+3 \\ 5& 9 & 81+5 \end{vmatrix}$

$\begin{vmatrix} 2 &7 &63+2 \\ 3& 8 &72+3 \\ 5& 9 & 81+5 \end{vmatrix} = \begin{vmatrix} 2 & 7 &2 \\ 3& 8& 3\\ 5 & 9 & 5 \end{vmatrix} + \begin{vmatrix} 2 & 7 &63 \\ 3& 8 &72 \\ 5 & 9 & 81 \end{vmatrix}$

$\begin{vmatrix} 2 & 7 &2 \\ 3& 8& 3\\ 5 & 9 & 5 \end{vmatrix} = 0$ [ $\because$ Here two columns are identical ]

and $\begin{vmatrix} 2 & 7 &63 \\ 3& 8 &72 \\ 5 & 9 & 81 \end{vmatrix} = \begin{vmatrix} 2 & 7 &9(7) \\ 3& 8 &9(8) \\ 5 &9 & 9(9) \end{vmatrix} = 9 \begin{vmatrix} 2 & 7 &7 \\ 3& 8& 8\\ 5& 9&9 \end{vmatrix}$ [ $\because$ Here two columns are identical ]

$= 0$

Therefore we have the value of determinant = 0.

Question:4 Using the property of determinants and without expanding, prove that

$\begin{vmatrix}1 &bc &a(b+c) \\1 &ca &b(c+a) \\1 &ab & c(a+b) \end{vmatrix}=0$

Answer:

We have determinant:

$\triangle = \begin{vmatrix} 1 &bc &a(b+c) \\ 1& ca &b(c+a) \\ 1& ab &c(a+b) \end{vmatrix}$

Applying $C_{3} \rightarrow C_{2} + C_{3}$ we have then;

$\triangle = \begin{vmatrix} 1 &bc & ab+bc+ca \\ 1& ca &ab+bc+ca \\ 1& ab &ab+bc+ca \end{vmatrix}$

So, here column 3 and column 1 are proportional.

Therefore, $\triangle = 0$ .

Question:5 Using the property of determinants and without expanding, prove that

$\begin{vmatrix}b+c &q+r &y+z \\ c+a & r+p &z+x \\ a+b &p+q & x+y \end{vmatrix}=2\begin{vmatrix} a &p &x \\ b &q &y \\ c &r & z \end{vmatrix}$

Answer:

Given determinant :

$\triangle= \begin{vmatrix}b+c &q+r &y+z \\ c+a & r+p &z+x \\ a+b &p+q & x+y \end{vmatrix}$

Splitting the third row; we get,

$= \begin{vmatrix}b+c &q+r &y+z \\ c+a & r+p &z+x \\ a &p & x \end{vmatrix} + \begin{vmatrix}b+c &q+r &y+z \\ c+a & r+p &z+x \\ b &q & y \end{vmatrix} = \triangle_{1} + \triangle_{2}\ (assume\ that)$ .

Then we have,

$\triangle_{1} = \begin{vmatrix} b+c & q+r & y+z \\ c+a & r+p & z+x \\ a &p & x \end{vmatrix}$

On Applying row transformation $R_{2} \rightarrow R_{2} - R_{3}$ and then $R_{1} \rightarrow R_{1} - R_{2}$ ;

we get, $\triangle_{1} = \begin{vmatrix} b & q & y \\ c & r & z \\ a &p & x \end{vmatrix}$

Applying Rows exchange transformation $R_{1} \leftrightarrow R_{2}$ and $R_{2} \leftrightarrow R_{3}$ , we have:

$\triangle_{1} =(-1)^2 \begin{vmatrix} b & q & y \\ c & r & z \\ a &p & x \end{vmatrix}= \begin{vmatrix} a & p & x\\ b & q&y \\ c& r & z \end{vmatrix}$

also $\triangle_{2} = \begin{vmatrix} b+c & q+r & y+z \\ c+a&r+p &z+x \\ b & q & y \end{vmatrix}$

On applying rows transformation, $R_{1} \rightarrow R_{1} - R_{3}$ and then $R_{2} \rightarrow R_{2} - R_{1}$

$\triangle_{2} = \begin{vmatrix} c & r & z \\ c+a&r+p &z+x \\ b & q & y \end{vmatrix}$ and then $\triangle_{2} = \begin{vmatrix} c & r & z \\ a&p &x \\ b & q & y \end{vmatrix}$

Then applying rows exchange transformation;

$R_{1} \leftrightarrow R_{2}$ and then $R_{2} \leftrightarrow R_{3}$ . we have then;

$\triangle_{2} =(-1)^2 \begin{vmatrix} a & p & x \\ b&q &y \\ c & r & z \end{vmatrix}$

So, we now calculate the sum = $\triangle_{1} + \triangle _{2}$

$\triangle_{1} + \triangle _{2} = 2 \begin{vmatrix} a &p &x \\ b& q& y\\ c & r& z \end{vmatrix}$

Hence proved.

Question:6 Using the property of determinants and without expanding, prove that

$\begin{vmatrix} 0 &a &-b \\-a &0 & -c\\b &c &0 \end{vmatrix}=0$

Answer:

We have given determinant

$\triangle = \begin{vmatrix} 0 &a &-b \\-a &0 & -c\\b &c &0 \end{vmatrix}$

Applying transformation, $\dpi{100} R_{1} \rightarrow cR_{1}$ we have then,

$\triangle = \frac{1}{c}\begin{vmatrix} 0 &ac &-bc \\-a &0 & -c\\b &c &0 \end{vmatrix}$

We can make the first row identical to the third row so,

Taking another row transformation: $R_{1} \rightarrow R_{1}-bR_{2}$ we have,

$\triangle = \frac{1}{c}\begin{vmatrix} ab &ac &0 \\-a &0 & -c\\b &c &0 \end{vmatrix} = \frac{a}{c} \begin{vmatrix} b &c &0 \\-a &0 & -c\\b &c &0 \end{vmatrix}$

So, determinant has two rows $R_{1}\ and\ R_{3}$ identical.

Hence $\triangle = 0$ .

Question:7 Using the property of determinants and without expanding, prove that

$\begin{vmatrix} -a^2 &ab &ac \\ ba &-b^2 &bc \\ ca & cb & -c^2 \end{vmatrix}=4a^2b^2c^2$

Answer:

Given determinant : $\dpi{100} \begin{vmatrix} -a^2 &ab &ac \\ ba &-b^2 &bc \\ ca & cb & -c^2 \end{vmatrix}$

$\triangle = \begin{vmatrix} -a^2 &ab &ac \\ ba &-b^2 &bc \\ ca & cb & -c^2 \end{vmatrix}$

As we can easily take out the common factors a,b,c from rows $R_{1},R_{2},R_{3}$ respectively.

So, get then:

$=abc \begin{vmatrix} -a &b &c \\ a &-b &c \\ a & b & -c \end{vmatrix}$

Now, taking common factors a,b,c from the columns $C_{1},C_{2},C_{3}$ respectively.

$=a^2b^2c^2 \begin{vmatrix} -1 &1 &1 \\ 1 &-1 &1 \\ 1 & 1 & -1 \end{vmatrix}$

Now, applying rows transformations $R_{1} \rightarrow R_{1} + R_{2}$ and then $R_{3} \rightarrow R_{2} + R_{3}$ we have;

$\triangle = a^2b^2c^2\begin{vmatrix} 0 &0 &2 \\ 1&-1 &1 \\ 2& 0 &0 \end{vmatrix}$

Expanding to get R.H.S.

$\triangle = a^2b^2c^2 \left ( 2\begin{vmatrix} 1 &-1 \\ 2& 0 \end{vmatrix} \right ) = 2a^2b^2c^2(0+2) =4a^2b^2c^2$

Question:8(i) By using properties of determinants, show that:

$\begin{vmatrix} 1 &a &a^2 \\ 1 &b &b^2 \\ 1 &c &c^2 \end{vmatrix}=(a-b)(b-c)(c-a)$
Answer:

We have the determinant $\dpi{100} \begin{vmatrix} 1 &a &a^2 \\ 1 &b &b^2 \\ 1 &c &c^2 \end{vmatrix}$

Applying the row transformations $R_{1} \rightarrow R_{1} -R_{2}$ and then $R_{2} \rightarrow R_{2} -R_{3}$ we have:

$\triangle = \begin{vmatrix} 0 &a-b &a^2-b^2 \\ 0 &b-c &b^2-c^2 \\ 1 &c &c^2 \end{vmatrix}$

$= \begin{vmatrix} 0 &a-b &(a-b)(a+b) \\ 0 &b-c &(b-c)(b+c) \\ 1 &c &c^2 \end{vmatrix} = (a-b)(b-c)\begin{vmatrix} 0 &1 &(a+b) \\ 0 &1 &(b+c) \\ 1 &c &c^2 \end{vmatrix}$

Now, applying $R_{1} \rightarrow R_{1} -R_{2}$ we have:

$= (a-b)(b-c)\begin{vmatrix} 0 &0 &(a-c) \\ 0 &1 &(b+c) \\ 1 &c &c^2 \end{vmatrix}$ or $= (a-b)(b-c)(a-c)\begin{vmatrix} 0 &0 &1 \\ 0 &1 &(b+c) \\ 1 &c &c^2 \end{vmatrix} =(a-b)(b-c)(a-c)\begin{vmatrix} 0 &1 \\ 1 & c \end{vmatrix}$

$= (a-b)(b-c)(c-a)$

Hence proved.

Question:8(ii) By using properties of determinants, show that:

$\dpi{100} \begin{vmatrix} 1 & 1 & 1\\ a & b & c\\ a^3 &b^3 &c^3 \end{vmatrix}=(a-b)(b-c)(c-a)(a+b+c)$

Answer:

Given determinant :

$\begin{vmatrix} 1 & 1 & 1\\ a & b & c\\ a^3 &b^3 &c^3 \end{vmatrix}$ ,

Applying column transformation $C_{1} \rightarrow C_{1}-C_{3}$ and then $C_{2} \rightarrow C_{2}-C_{3}$

We get,

$\triangle =\begin{vmatrix} 0 & 0 & 1\\ a-c& b-c & c \\ a^3-c^3 &b^3-c^3 & c^3 \end{vmatrix}$

$=\begin{vmatrix} 0 & 0 & 1\\ a-c& b-c & c \\ (a-c)(a^2+ac+c^2) &(b-c)(b^2+bc+c^2) & c^3 \end{vmatrix}$

$=(a-c)(b-c)\begin{vmatrix} 0 & 0 & 1\\ 1& 1 & c \\ (a^2+ac+c^2) &(b^2+bc+c^2) & c^3 \end{vmatrix}$

Now, applying column transformation $C_{1} \rightarrow C_{1} - C_{2}$ , we have:

$=(a-c)(b-c)\begin{vmatrix} 0 & 0 & 1\\ 0& 1 & c \\ (a^2-b^2+ac-bc) &(b^2+bc+c^2) & c^3 \end{vmatrix}$

$=(a-c)(b-c)\begin{vmatrix} 0 & 0 & 1\\ 0& 1 & c \\ (a-b)(a+b+c) &(b^2+bc+c^2) & c^3 \end{vmatrix}$

$=(a-c)(b-c)(a-b)(a+b+c)\begin{vmatrix} 0&1 \\ 1& c \end{vmatrix}$

$=-(a-c)(b-c)(a-b)(a+b+c) = (a-b)(b-c)(c-a)(a+b+c)$

Hence proved.

Question:9 By using properties of determinants, show that:

$\begin{vmatrix} x & x^2 & yz\\ y & y^2 &zx \\ z & z^2 & xy \end{vmatrix}=(x-y)(y-z)(z-x)(xy+yz+zx)$

Answer:

We have the determinant:

$\triangle = \begin{vmatrix} x & x^2 & yz\\ y & y^2 &zx \\ z & z^2 & xy \end{vmatrix}$

Applying the row transformations $R_{1} \rightarrow R_{1}- R_{3}$ and then $R_{2} \rightarrow R_{2}- R_{3}$ , we have;

$\triangle = \begin{vmatrix} x-z & x^2-z^2 & yz-xy\\ y-z & y^2-z^2 &zx-xy \\ z & z^2 & xy \end{vmatrix}$

$= \begin{vmatrix} x-z & (x-z)(x+z) & y(z-x)\\ y-z & (y-z)(y+z) &x(z-y) \\ z & z^2 & xy \end{vmatrix}$

$= (x-z)(y-z)\begin{vmatrix} 1 & (x+z) & -y\\ 1 & (y+z) &-x \\ z & z^2 & xy \end{vmatrix}$

Now, applying $R_{1} \rightarrow R_{1} - R_{2}$ ; we have

$= (x-z)(y-z)\begin{vmatrix} 0 & (x-y) & (x-y)\\ 1 & (y+z) &-x \\ z & z^2 & xy \end{vmatrix}$

$= (x-z)(y-z)(x-y)\begin{vmatrix} 0 & 1 & 1\\ 1 & (y+z) &-x \\ z & z^2 & xy \end{vmatrix}$

Now, expanding the remaining determinant;

$= (x-z)(y-z)(x-y) \left [ (xy+zx) + (z^2 - zy-z^2) \right]$

$= -(x-z)(y-z)(x-y) \left [ xy+zx + zy \right]$

$= (x-y)(y-z)(z-x) \left [ xy+zx + zy \right]$

Hence proved.

Question:10(i) By using properties of determinants, show that:

$\begin{vmatrix} x+4 &2x &2x \\ 2x & x+4 & 2x\\ 2x & 2x & x+4 \end{vmatrix}=(5x+4)(4-x)$

Answer:

Given determinant:

$\begin{vmatrix} x+4 &2x &2x \\ 2x & x+4 & 2x\\ 2x & 2x & x+4 \end{vmatrix}$

Applying row transformation: $R_{1} \rightarrow R_{1} + R_{2} + R_{3}$ then we have;

$\triangle = \begin{vmatrix} 5x+4 &5x+4 &5x+4 \\ 2x & x+4 & 2x\\ 2x & 2x & x+4 \end{vmatrix}$

Taking a common factor: 5x+4

$= (5x+4)\begin{vmatrix} 1 &1 &1 \\ 2x & x+4 & 2x\\ 2x & 2x & x+4 \end{vmatrix}$

Now, applying column transformations $C_{1} \rightarrow C_{1}- C_{2}$ and $C_{2} \rightarrow C_{2}- C_{3}$

$= (5x+4)\begin{vmatrix} 0 &0 &1 \\ x-4 & 4-x & 2x\\ 0 & x-4 & x+4 \end{vmatrix}$

$= (5x+4)(4-x)(4-x)\begin{vmatrix} 0 &0 &1 \\ 1 & 1 & 2x\\ 0 & 1 & x+4 \end{vmatrix}$

$= (5x+4)(4-x)^2$

Question:10(ii) By using properties of determinants, show that:

$\begin{vmatrix} y+k & y & y\\ y & y+k &y \\ y & y & y+k \end{vmatrix}=k^2(3y+k)$

Answer:

Given determinant:

$\triangle = \begin{vmatrix} y+k & y & y\\ y & y+k &y \\ y & y & y+k \end{vmatrix}$

Applying row transformation $R_{1} \rightarrow R_{1} +R_{2}+R_{3}$ we get;

$= \begin{vmatrix} 3y+k & 3y+k & 3y+k\\ y & y+k &y \\ y & y & y+k \end{vmatrix}$

$=(3y+k) \begin{vmatrix}1 & 1 & 1\\ y & y+k &y \\ y & y & y+k \end{vmatrix}$ [taking common (3y + k) factor]

Now, applying column transformation $C_{1} \rightarrow C_{1} - C_{2}$ and $C_{2} \rightarrow C_{2} - C_{3}$

$=(3y+k) \begin{vmatrix}0 & 0 & 1\\ -k & k &y \\ 0 & -k & y+k \end{vmatrix}$

$=(3y+k)(k^2) \begin{vmatrix}0 & 0 & 1\\ -1 & 1 &y \\ 0 & -1 & y+k \end{vmatrix}$

$=k^2 (3y+k)$

Hence proved.

Question:11(i) By using properties of determinants, show that:

$\begin{vmatrix} a-b-c &2a &2a \\ 2b &b-c-a &2b \\ 2c &2c &c-a-b \end{vmatrix}=(a+b+c)^3$

Answer:

Given determinant:

$\triangle = \begin{vmatrix} a-b-c &2a &2a \\ 2b &b-c-a &2b \\ 2c &2c &c-a-b \end{vmatrix}$

We apply row transformation: $R_{1} \rightarrow R_{1}+R_{2}+R_{3}$ we have;

$= \begin{vmatrix} a+b+c &a+b+c &a+b+c \\ 2b &b-c-a &2b \\ 2c &2c &c-a-b \end{vmatrix}$

Taking common factor (a+b+c) out.

$=(a+b+c) \begin{vmatrix} 1 &1 &1 \\ 2b &b-c-a &2b \\ 2c &2c &c-a-b \end{vmatrix}$

Now, applying column tranformation $C_{1} \rightarrow C_{1}- C_{2}$ and then $C_{2} \rightarrow C_{2}- C_{3}$

We have;

$=(a+b+c) \begin{vmatrix} 0 &0 &1 \\ b+c+a &-b-c-a &2b \\ 0 &c+a+b &c-a-b \end{vmatrix}$

$=(a+b+c)(a+b+c)(a+b+c) \begin{vmatrix} 0 &0 &1 \\ 1 &-1 &2b \\ 0 &1 &c-a-b \end{vmatrix}$

$=(a+b+c)(a+b+c)(a+b+c) = (a+b+c)^3$

Hence Proved.

Question:11(ii) By using properties of determinants, show that:

$\begin{vmatrix} x+y+2z &x &y \\ z & y+z+2x & y\\ z & x &z+x+2y \end{vmatrix}=2(x+y+z)^3$

Answer:

Given determinant

$\triangle =\begin{vmatrix} x+y+2z &x &y \\ z & y+z+2x & y\\ z & x &z+x+2y \end{vmatrix}$

Applying $C_{1} \rightarrow C_{1}+C_{2}+C_{3}$ we get;

$=\begin{vmatrix} 2(x+y+z) &x &y \\ 2(z+y+x) & y+z+2x & y\\ 2(z+y+x) & x &z+x+2y \end{vmatrix}$

Taking 2(x+y+z) factor out, we get;

$=2(x+y+z)\begin{vmatrix} 1 &x &y \\ 1 & y+z+2x & y\\ 1 & x &z+x+2y \end{vmatrix}$

Now, applying row transformations, $R_{1} \rightarrow R_{1} -R_{2}$ and then $R_{2} \rightarrow R_{2} -R_{3}$ .

we get;

$=2(x+y+z)\begin{vmatrix} 0 &-x-y-z &0 \\ 0 & y+z+x & -y-z-x\\ 1 & x &z+x+2y \end{vmatrix}$

$=2(x+y+z)^3\begin{vmatrix} 0 &-1 &0 \\ 0 & 1 & -1\\ 1 & x &z+x+2y \end{vmatrix}$

$=2(x+y+z)^3\begin{vmatrix} -1 &0 \\ 1& -1 \end{vmatrix} = 2(x+y+z)^3$

Hence proved.

Question:12 By using properties of determinants, show that:

$\begin{vmatrix} 1 &x &x^2 \\ x^2 &1 &x \\ x &x^2 &1 \end{vmatrix}=(1-x^3)^2$

Answer:

Give determinant $\begin{vmatrix} 1 &x &x^2 \\ x^2 &1 &x \\ x &x^2 &1 \end{vmatrix}$

Applying column transformation $C_{1} \rightarrow C_{1}+C_{2}+C_{3}$ we get;

$\triangle = \begin{vmatrix} 1+x+x^2 &x &x^2 \\ x^2+1+x &1 &x \\ x+x^2+1 &x^2 &1 \end{vmatrix}$

$= (1+x+x^2)\begin{vmatrix} 1 &x &x^2 \\ 1 &1 &x \\ 1 &x^2 &1 \end{vmatrix}$ [ after taking the (1+x+x ² ) factor common out.]

Now, applying row transformations, $R_{1} \rightarrow R_{1}-R_{2}$ and then $R_{2} \rightarrow R_{2}-R_{3}$ .

we have now,

$= (1+x+x^2)\begin{vmatrix} 0 &x-1 &x^2-x \\ 0 &1-x^2 &x-1 \\ 1 &x^2 &1 \end{vmatrix}$

$= (1+x+x^2)\begin{vmatrix} x-1 &x^2-x \\ 1-x^2 &x-1 \end{vmatrix}$

$= (1+x+x^2)((x-1)^2-x(x-1)(1-x^2))$

$= (1+x+x^2)(x-1)(x^3-1) = (x^3-1)^2$

As we know $\left [\because (1+x+x^2)(x-1) = (x^3-1) \right ]$

Hence proved.

Question:13 By using properties of determinants, show that:

$\begin{vmatrix} 1+a^2-b^2 &2ab &-2b \\ 2ab &1-a^2+b^2 &2a \\ 2b &-2a & 1-a^2-b^2 \end{vmatrix}=(1+a^2+b^2)^3$

Answer:

We have determinant:

$\triangle = \begin{vmatrix} 1+a^2-b^2 &2ab &-2b \\ 2ab &1-a^2+b^2 &2a \\ 2b &-2a & 1-a^2-b^2 \end{vmatrix}$

Applying row transformations, $R_{1} \rightarrow R_{1} +bR_{3}$ and $R_{2} \rightarrow R_{2} -aR_{3}$ then we have;

$= \begin{vmatrix} 1+a^2+b^2 &0 &-b(1+a^2+b^2) \\ 0 &1+a^2+b^2 &a(1+a^2+b^2) \\ 2b &-2a & 1-a^2-b^2 \end{vmatrix}$

taking common factor out of the determinant;

$= (1+a^2+b^2)^2\begin{vmatrix} 1 &0 &-b \\ 0 &1 &a \\ 2b &-2a & 1-a^2-b^2 \end{vmatrix}$

Now expanding the remaining determinant we get;

$= (1+a^2+b^2)^2\left [ (1)\begin{vmatrix} 1& a\\ -2a&1-a^2-b^2 \end{vmatrix} - b\begin{vmatrix} 0&1 \\ 2b&-2a \end{vmatrix}\right ]$

$= (1+a^2+b^2)^2\left [ 1-a^2-b^2+2a^2-b(-2b)\right ]$

$= (1+a^2+b^2)^2\left [ 1+a^2+b^2\right ] = (1+a^2+b^2)^3$

Hence proved.

Question:14 By using properties of determinants, show that:

$\begin{vmatrix} a^2+1 &ab &ac \\ ab &b^2+1 &bc \\ ca & cb &c^2+1 \end{vmatrix}=1+a^2+b^2+c^2$

Answer:

Given determinant:

$\dpi{100} \begin{vmatrix} a^2+1 &ab &ac \\ ab &b^2+1 &bc \\ ca & cb &c^2+1 \end{vmatrix}$

Let $\triangle = \begin{vmatrix} a^2+1 &ab &ac \\ ab &b^2+1 &bc \\ ca & cb &c^2+1 \end{vmatrix}$

Then we can clearly see that each column can be reduced by taking common factors like a,b, and c respectively from C _1, C _2, and C _3.

We then get;

$=abc \begin{vmatrix} \left ( a+\frac{1}{a} \right ) &a &a \\ b &(b+\frac{1}{b}) &b \\ c & c &(c+\frac{1}{c}) \end{vmatrix}$

Now, applying column transformations: $C_{1} \rightarrow C_{1} -C_{2}$ and $C_{2} \rightarrow C_{2} -C_{3}$

then we have;

$=abc \begin{vmatrix} \left ( \frac{1}{a} \right ) &0 &a \\ -\frac{1}{b} &(\frac{1}{b}) &b \\ 0 & -\frac{1}{c} &(c+\frac{1}{c}) \end{vmatrix}$

$=abc\times \frac{1}{abc} \begin{vmatrix} 1 &0 &a^2 \\ -1 &1 &b^2 \\ 0 & -1 &(c^2+1) \end{vmatrix}$

$= \begin{vmatrix} 1 &0 &a^2 \\ -1 &1 &b^2 \\ 0 & -1 &(c^2+1) \end{vmatrix}$

Now, expanding the remaining determinant:

$\triangle = 1\begin{vmatrix} 1&b^2 \\ -1&(c^2+1) \end{vmatrix} + a^2\begin{vmatrix} -1&1 \\ 0& -1 \end{vmatrix}$

$= 1[(c^2+1)+b^2] + a^2(1)=a^2+b^2+c^2+1$ .

Hence proved.

Question:15 Choose the correct answer. Let A be a square matrix of order $3\times 3$ , then $|kA|$ is equal to

(A) $k|A|$ (B) $k^2|A|$ (C) $k^3|A|$ (D) $3k|A|$

Answer:

Assume a square matrix A of order of $3\times3$ .

$A = \begin{bmatrix} a_1 & b_1&c_1 \\ a_2& b_2& c_2\\ a_3& b_3 & c_3 \end{bmatrix}$

Then we have;

$kA = \begin{bmatrix} ka_1 & kb_1&kc_1 \\ ka_2& kb_2& kc_2\\ ka_3& kb_3 & kc_3 \end{bmatrix}$

( Taking the common factors k from each row. )

$|kA| = \begin{vmatrix} ka_1 & kb_1&kc_1 \\ ka_2& kb_2& kc_2\\ ka_3& kb_3 & kc_3 \end{vmatrix} = k^3 \begin{vmatrix} a_1 & b_1&c_1 \\a_2& b_2& c_2\\ a_3& b_3 & c_3 \end{vmatrix}$

$= k^3 |A|$

Therefore correct option is (C).

Question:16 Choose the correct answer.

Which of the following is correct
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these

Answer:

The answer is (C) Determinant is a number associated to a square matrix.

As we know that To every square matrix $A = [a_{ij}]$ of order n, we can associate a number (real or complex) called determinant of the square matrix A, where $a_{ij} = (i, j)^{th}$ element of A.

NCERT class 12 maths chapter 4 question answer: Excercise-4.3

Question:1(i) Find area of the triangle with vertices at the point given in each of the following :

$(1,0), (6,0), (4,3)$

Answer:

We can find the area of the triangle with vertices $(1,0), (6,0), (4,3)$ by the following determinant relation:

$\triangle =\frac{1}{2} \begin{vmatrix} 1& 0 &1 \\ 6 & 0 &1 \\ 4& 3& 1 \end{vmatrix}$

Expanding using second column

$=\frac{1}{2} (-3) \begin{vmatrix} 1 &1 & \\ 6& 1 & \end{vmatrix}$

$= \frac{15}{2}\ square\ units.$

Question:1(ii) Find area of the triangle with vertices at the point given in each of the following :

$(2,7), (1,1), (10,8)$

Answer:

We can find the area of the triangle with given coordinates by the following method:

$\triangle = \begin{vmatrix} 2 &7 &1 \\ 1 & 1& 1\\ 10& 8 &1 \end{vmatrix}$

$=\frac{1}{2} \begin{vmatrix} 2 &7 &1 \\ 1 & 1& 1\\ 10& 8 &1 \end{vmatrix} = \frac{1}{2}\left [ 2(1-8)-7(1-10)+1(8-10) \right ]$

$= \frac{1}{2}\left [ 2(-7)-7(-9)+1(-2) \right ] = \frac{1}{2}\left [ -14+63-2 \right ] = \frac{47}{2}\ square\ units.$

Question:1(iii) Find area of the triangle with vertices at the point given in each of the following :

$(-2,-3), (3,2), (-1,-8)$

Answer:

Area of the triangle by the determinant method:

$Area\ \triangle = \frac{1}{2} \begin{vmatrix} -2 &-3 &1 \\ 3& 2 & 1\\ -1& -8 & 1 \end{vmatrix}$

$=\frac{1}{2}\left [ -2(2+8)+3(3+1)+1(-24+2) \right ]$

$=\frac{1}{2}\left [ -20+12-22 \right ] = \frac{1}{2}[-30]= -15$

Hence the area is equal to $|-15| = 15\ square\ units.$

Question:2 Show that points $A (a, b+c), B (b,c+a), C (c,a+b)$ are collinear.

Answer:

If the area formed by the points is equal to zero then we can say that the points are collinear.

So, we have an area of a triangle given by,

$\triangle = \frac{1}{2} \begin{vmatrix} a &b+c &1 \\ b& c+a &1 \\ c& a+b & 1 \end{vmatrix}$

calculating the area:

$= \frac{1}{2}\left [ a\begin{vmatrix} c+a &1 \\ a+b& 1 \end{vmatrix} - (b+c)\begin{vmatrix} b & 1\\ c&1 \end{vmatrix}+1\begin{vmatrix} b &c+a \\ c&a+b \end{vmatrix} \right ]$

$= \frac{1}{2}\left [ a(c+a-a-b) - (b+c)(b-c)+1(b(a+b)-c(c+a)) \right ]$

$= \frac{1}{2}\left [ ac-ab - b^2+c^2+ab+b^2-c^2-ac \right ] = \frac{1}{2} \left [ 0 \right] = 0$

Hence the area of the triangle formed by the points is equal to zero.

Therefore given points $A (a, b+c), B (b,c+a), C (c,a+b)$ are collinear.

Question:3(i) Find values of k if area of triangle is 4 sq. units and vertices are

$(k,0), (4,0), (0,2)$

Answer:

We can easily calculate the area by the formula :

$\triangle = \frac{1}{2} \begin{vmatrix} k &0 &1 \\ 4& 0& 1\\ 0 &2 & 1 \end{vmatrix} = 4\ sq.\ units$

$= \frac{1}{2}\left [ k\begin{vmatrix} 0 &1 \\ 2& 1 \end{vmatrix} -0\begin{vmatrix} 4 &1 \\ 0 & 1 \end{vmatrix}+1\begin{vmatrix} 4 &0 \\ 0& 2 \end{vmatrix} \right ]= 4\ sq.\ units$

$=\frac{1}{2}\left [ k(0-2)-0+1(8-0) \right ] = \frac{1}{2}\left [ -2k+8 \right ] = 4\ sq.\ units$

$\left [ -2k+8 \right ] = 8\ sq.\ units$ or $-2k +8 = \pm 8\ sq.\ units$

or $k = 0$ or $k = 8$

Hence two values are possible for k.

Question:3(ii) Find values of k if area of triangle is 4 sq. units and vertices are

$(-2,0), (0,4), (0,k)$

Answer:

The area of the triangle is given by the formula:

$\triangle = \frac{1}{2} \begin{vmatrix} -2 &0 &1 \\ 0 & 4 & 1\\ 0& k & 1 \end{vmatrix} = 4\ sq.\ units.$

Now, calculating the area:

$= \frac{1}{2} \left | -2(4-k)-0(0-0)+1(0-0) \right | = \frac{1}{2} \left | -8+2k \right | = 4$

or $-8+2k =\pm 8$

Therefore we have two possible values of 'k' i.e., $k = 8$ or $k = 0$ .

Question:4(i) Find equation of line joining $\small (1,2)$ and $\small (3,6)$ using determinants.

Answer:

As we know the line joining $\small (1,2)$ , $\small (3,6)$ and let say a point on line $A\left ( x,y \right )$ will be collinear.

Therefore area formed by them will be equal to zero.

$\triangle = \frac{1}{2}\begin{vmatrix} 1 &2 &1 \\ 3& 6 &1 \\ x & y &1 \end{vmatrix} = 0$

So, we have:

$=1(6-y)-2(3-x)+1(3y-6x) = 0$

or $6-y-6+2x+3y-6x = 0 \Rightarrow 2y-4x=0$

Hence, we have the equation of line $\Rightarrow y=2x$ .

Question:4(ii) Find equation of line joining $\small (3,1)$ and $\small (9,3)$ using determinants.

Answer:

We can find the equation of the line by considering any arbitrary point $A(x,y)$ on line.

So, we have three points which are collinear and therefore area surrounded by them will be equal to zero .

$\triangle = \frac{1}{2}\begin{vmatrix} 3 &1 &1 \\ 9& 3 & 1\\ x& y &1 \end{vmatrix} = 0$

Calculating the determinant:

$=\frac{1}{2}\left [ 3\begin{vmatrix} 3 &1 \\ y& 1 \end{vmatrix}-1\begin{vmatrix} 9 &1 \\ x& 1 \end{vmatrix}+1\begin{vmatrix} 9 &3 \\ x &y \end{vmatrix} \right ]$

$=\frac{1}{2}\left [ 3(3-y)-1(9-x)+1(9y-3x) \right ] = 0$

$\frac{1}{2}\left [ 9-3y-9+x+9y-3x \right ] = \frac{1}{2}[6y-2x] = 0$

Hence we have the line equation:

$3y= x$ or $x-3y = 0$ .

Question:5 If the area of triangle is 35 sq units with vertices $\small (2,-6),(5,4)$ and $\small (k,4)$ . Then k is

(A) $\small 12$ (B) $\small -2$ (C) $\small -12,-2$ (D) $\small 12,-2$

Answer:

Area of triangle is given by:

$\triangle = \frac{1}{2} \begin{vmatrix} 2 &-6 &1 \\ 5& 4 & 1\\ k& 4& 1 \end{vmatrix} = 35\ sq.\ units.$

or $\begin{vmatrix} 2 &-6 &1 \\ 5& 4 & 1\\ k& 4& 1 \end{vmatrix} = 70\ sq.\ units.$

$2\begin{vmatrix} 4 &1 \\ 4& 1 \end{vmatrix}-(-6)\begin{vmatrix} 5 &1 \\ k &1 \end{vmatrix}+1\begin{vmatrix} 5 &4 \\ k&4 \end{vmatrix} = 70$

$2(4-4) +6(5-k)+(20-4k) = \pm70$

$50-10k = \pm70$

$k = 12$ or $k = -2$

Hence the possible values of k are 12 and -2.

Therefore option (D) is correct.

NCERT class 12 maths chapter 4 question answer: Excercise: 4.4

Question:1(i) Write Minors and Cofactors of the elements of following determinants:

$\small \begin{vmatrix}2 &-4 \\0 &3 \end{vmatrix}$

Answer:

GIven determinant: $\begin{vmatrix}2 &-4 \\0 &3 \end{vmatrix}$

Minor of element $a_{ij}$ is $M_{ij}$ .

Therefore we have

$M_{11}$ = minor of element $a_{11}$ = 3

$M_{12}$ = minor of element $a_{12}$ = 0

$M_{21}$ = minor of element $a_{21}$ = -4

$M_{22}$ = minor of element $a_{22}$ = 2

and finding cofactors of $a_{ij}$ is $A_{ij}$ = $(-1)^{i+j}M_{ij}$ .

Therefore we have:

$A_{11} = (-1)^{1+1}M_{11} = (-1)^2(3) = 3$

$A_{12} = (-1)^{1+2}M_{12} = (-1)^3(0) = 0$

$A_{21} = (-1)^{2+1}M_{21} = (-1)^3(-4) = 4$

$A_{22} = (-1)^{2+2}M_{22} = (-1)^4(2) = 2$

Question:1(ii) Write Minors and Cofactors of the elements of following determinants:

$\small \begin{vmatrix} a &c \\ b &d \end{vmatrix}$

Answer:

GIven determinant: $\begin{vmatrix} a &c \\ b &d \end{vmatrix}$

Minor of element $a_{ij}$ is $M_{ij}$ .

Therefore we have

$M_{11}$ = minor of element $a_{11}$ = d

$M_{12}$ = minor of element $a_{12}$ = b

$M_{21}$ = minor of element $a_{21}$ = c

$M_{22}$ = minor of element $a_{22}$ = a

and finding cofactors of $a_{ij}$ is $A_{ij}$ = $(-1)^{i+j}M_{ij}$ .

Therefore we have:

$A_{11} = (-1)^{1+1}M_{11} = (-1)^2(d) = d$

$A_{12} = (-1)^{1+2}M_{12} = (-1)^3(b) = -b$

$A_{21} = (-1)^{2+1}M_{21} = (-1)^3(c) = -c$

$A_{22} = (-1)^{2+2}M_{22} = (-1)^4(a) = a$

Question:2(i) Write Minors and Cofactors of the elements of following determinants:

$\small \begin{vmatrix} 1 & 0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{vmatrix}$

Answer:

Given determinant : $\begin{vmatrix} 1 & 0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{vmatrix}$

Finding Minors: by the definition,

$M_{11} =$ minor of $a_{11} = \begin{vmatrix} 1 &0 \\ 0 &1 \end{vmatrix} = 1$ $M_{12} =$ minor of $a_{12} = \begin{vmatrix} 0 &0 \\ 0 &1 \end{vmatrix} = 0$

$M_{13} =$ minor of $a_{13} = \begin{vmatrix} 0 &1 \\ 0 &0 \end{vmatrix} = 0$ $M_{21} =$ minor of $a_{21} = \begin{vmatrix} 0 &0 \\ 0 &1 \end{vmatrix} = 0$

$M_{22} =$ minor of $a_{22} = \begin{vmatrix} 1 &0 \\ 0 &1 \end{vmatrix} = 1$ $M_{23} =$ minor of $a_{23} = \begin{vmatrix} 1 &0 \\ 0 &0 \end{vmatrix} = 0$

$M_{31} =$ minor of $a_{31} = \begin{vmatrix} 0 &0 \\ 1 &0 \end{vmatrix} = 0$ $M_{32} =$ minor of $a_{32} = \begin{vmatrix} 1 &0 \\ 0 &0 \end{vmatrix} = 0$

$M_{33} =$ minor of $a_{33} = \begin{vmatrix} 1 &0 \\ 0 &1 \end{vmatrix} = 1$

Finding the cofactors:

$A_{11}=$ cofactor of $a_{11} = (-1)^{1+1}M_{11} = 1$

$A_{12}=$ cofactor of $a_{12} = (-1)^{1+2}M_{12} = 0$

$A_{13}=$ cofactor of $a_{13} = (-1)^{1+3}M_{13} = 0$

$A_{21}=$ cofactor of $a_{21} = (-1)^{2+1}M_{21} = 0$

$A_{22}=$ cofactor of $a_{22} = (-1)^{2+2}M_{22} = 1$

$A_{23}=$ cofactor of $a_{23} = (-1)^{2+3}M_{23} = 0$

$A_{31}=$ cofactor of $a_{31} = (-1)^{3+1}M_{31} = 0$

$A_{32}=$ cofactor of $a_{32} = (-1)^{3+2}M_{32} = 0$

$A_{33}=$ cofactor of $a_{33} = (-1)^{3+3}M_{33} = 1$ .

Question:2(ii) Write Minors and Cofactors of the elements of following determinants:

$\small \begin{vmatrix} 1 &0 &4 \\ 3 & 5 &-1 \\ 0 &1 &2 \end{vmatrix}$

Answer:

Given determinant : $\begin{vmatrix} 1 &0 &4 \\ 3 & 5 &-1 \\ 0 &1 &2 \end{vmatrix}$

Finding Minors: by the definition,

$M_{11} =$ minor of $a_{11} = \begin{vmatrix} 5 &-1 \\ 1 &2 \end{vmatrix} = 11$ $M_{12} =$ minor of $a_{12} = \begin{vmatrix} 3 &-1 \\ 0 &2 \end{vmatrix} = 6$

$M_{13} =$ minor of $a_{13} = \begin{vmatrix} 3 &5 \\ 0 &1 \end{vmatrix} = 3$ $M_{21} =$ minor of $a_{21} = \begin{vmatrix} 0 &4 \\ 1 &2 \end{vmatrix} = -4$

$M_{22} =$ minor of $a_{22} = \begin{vmatrix} 1 &4 \\ 0 &2 \end{vmatrix} = 2$ $M_{23} =$ minor of $a_{23} = \begin{vmatrix} 1 &0 \\ 0 &1 \end{vmatrix} = 1$

$M_{31} =$ minor of $a_{31} = \begin{vmatrix} 0 &4 \\ 5 &-1 \end{vmatrix} = -20$

$M_{32} =$ minor of $a_{32} = \begin{vmatrix} 1 &4 \\ 3 &-1 \end{vmatrix} = -1-12=-13$

$M_{33} =$ minor of $a_{33} = \begin{vmatrix} 1 &0 \\ 3 &5 \end{vmatrix} = 5$

Finding the cofactors:

$A_{11}=$ cofactor of $a_{11} = (-1)^{1+1}M_{11} = 11$

$A_{12}=$ cofactor of $a_{12} = (-1)^{1+2}M_{12} = -6$

$A_{13}=$ cofactor of $a_{13} = (-1)^{1+3}M_{13} = 3$

$A_{21}=$ cofactor of $a_{21} = (-1)^{2+1}M_{21} = 4$

$A_{22}=$ cofactor of $a_{22} = (-1)^{2+2}M_{22} = 2$

$A_{23}=$ cofactor of $a_{23} = (-1)^{2+3}M_{23} = -1$

$A_{31}=$ cofactor of $a_{31} = (-1)^{3+1}M_{31} = -20$

$A_{32}=$ cofactor of $a_{32} = (-1)^{3+2}M_{32} = 13$

$A_{33}=$ cofactor of $a_{33} = (-1)^{3+3}M_{33} = 5$ .

Question:3 Using Cofactors of elements of second row, evaluate . $\small \Delta =\begin{vmatrix} 5 &3 &8 \\ 2 & 0 & 1\\ 1 &2 &3 \end{vmatrix}$

Answer:

Given determinant : $\small \Delta =\begin{vmatrix} 5 &3 &8 \\ 2 & 0 & 1\\ 1 &2 &3 \end{vmatrix}$

First finding Minors of the second rows by the definition,

$M_{21} =$ minor of $a_{21} = \begin{vmatrix} 3 &8 \\ 2 &3 \end{vmatrix} =9-16 = -7$

$M_{22} =$ minor of $a_{22} = \begin{vmatrix} 5 &8 \\ 1 &3 \end{vmatrix} = 15-8=7$

$M_{23} =$ minor of $a_{23} = \begin{vmatrix} 5 &3 \\ 1 &2 \end{vmatrix} = 10-3 =7$

Finding the Cofactors of the second row:

$A_{21}=$ Cofactor of $a_{21} = (-1)^{2+1}M_{21} = 7$

$A_{22}=$ Cofactor of $a_{22} = (-1)^{2+2}M_{22} = 7$

$A_{23}=$ Cofactor of $a_{23} = (-1)^{2+3}M_{23} = -7$

Therefore we can calculate $\triangle$ by sum of the product of the elements of the second row with their corresponding cofactors.

Therefore we have,

$\triangle = a_{21}A_{21} + a_{22}A_{22} + a_{23}A_{23} = 2(7) +0(7) +1(-7) =14-7=7$

Question:4 Using Cofactors of elements of third column, evaluate $\small \Delta =\begin{vmatrix} 1 &x &yz \\ 1 &y &zx \\ 1 &z &xy \end{vmatrix}$

Answer:

Given determinant : $\small \Delta =\begin{vmatrix} 1 &x &yz \\ 1 &y &zx \\ 1 &z &xy \end{vmatrix}$

First finding Minors of the third column by the definition,

$M_{13} =$ minor of $a_{13} = \begin{vmatrix} 1 &y \\ 1 &z \end{vmatrix} =z-y$

$M_{23} =$ minor of $a_{23} = \begin{vmatrix} 1 &x \\ 1 &z \end{vmatrix} = z-x$

$M_{33} =$ minor of $a_{33} = \begin{vmatrix} 1 &x \\ 1 &y \end{vmatrix} =y-x$

Finding the Cofactors of the second row:

$A_{13}=$ Cofactor of $a_{13} = (-1)^{1+3}M_{13} = z-y$

$A_{23}=$ Cofactor of $a_{23} = (-1)^{2+3}M_{23} = x-z$

$A_{33}=$ Cofactor of $a_{33} = (-1)^{3+3}M_{33} = y-x$

Therefore we can calculate $\triangle$ by sum of the product of the elements of the third column with their corresponding cofactors.

Therefore we have,

$\triangle = a_{13}A_{13} + a_{23}A_{23} + a_{33}A_{33}$

$= (z-y)yz + (x-z)zx +(y-x)xy$

$=yz^2-y^2z + zx^2-xz^2 + xy^2-x^2y$

$=z(x^2-y^2) + z^2(y-x) +xy(y-x)$

$= (x-y) \left [ zx+zy-z^2-xy \right ]$

$=(x-y)\left [ z(x-z) +y(z-x) \right ]$

$= (x-y)(z-x)[-z+y]$

$= (x-y)(y-z)(z-x)$

Thus, we have value of $\triangle = (x-y)(y-z)(z-x)$ .

Question:5 If $\small \Delta =\begin{vmatrix} a{_{11}} & a_1_2 & a_1_3\\ a_2_1 & a_2_2 & a_2_3\\ a_3_1 &a_3_2 &a_3_3 \end{vmatrix}$ and $\small A{_{ij}}$ is Cofactors of $\small a{_{ij}}$ , then the value of $\small \Delta$ is given by

(A) $\small a_1_1A_3_1+a_1_2A_3_2+a_1_3A_3_3$

(B) $\small a_1_1A_1_1+a_1_2A_2_1+a_1_3A_3_1$

(D) $\small a_1_1A_1_1+a_2_1A_2_1+a_3_1A_3_1$

Answer:

Answer is (D) $\small a_1_1A_1_1+a_2_1A_2_1+a_3_1A_3_1$ by the definition itself, $\small \Delta$ is equal to the product of the elements of the row/column with their corresponding cofactors.

NCERT determinants class 12 solutions: Excercise: 4.5

Question:1 Find adjoint of each of the matrices.

$\small \begin{bmatrix} 1 &2 \\ 3 & 4 \end{bmatrix}$

Answer:

Given matrix: $\small \begin{bmatrix} 1 &2 \\ 3 & 4 \end{bmatrix}= A$

Then we have,

$A_{11} = 4, A_{12}=-(1)3, A_{21} = -(1)2,\ and\ A_{22}= 1$

Hence we get:

$adjA = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} &A_{22} \end{bmatrix}^T = \begin{bmatrix} A_{11} & A_{21} \\ A_{12} &A_{22} \end{bmatrix} = \begin{bmatrix} 4 & -2 \\ -3 &1 \end{bmatrix}$

Question:2 Find adjoint of each of the matrices

$\small \begin{bmatrix} 1 &-1 &2 \\ 2 & 3 &5 \\ -2 & 0 &1 \end{bmatrix}$

Answer:

Given the matrix: $\small A = \begin{bmatrix} 1 &-1 &2 \\ 2 & 3 &5 \\ -2 & 0 &1 \end{bmatrix}$

Then we have,

$A_{11} = (-1)^{1+1}\begin{vmatrix} 3 &5 \\ 0& 1 \end{vmatrix} =(3-0)= 3$

$A_{12} = (-1)^{1+2}\begin{vmatrix} 2 &5 \\ -2& 1 \end{vmatrix} =-(2+10)= -12$

$A_{13} = (-1)^{1+3}\begin{vmatrix} 2 &3 \\ -2& 0 \end{vmatrix} =0+6= 6$

$A_{21} = (-1)^{2+1}\begin{vmatrix} -1 &2 \\ 0& 1 \end{vmatrix} =-(-1-0)= 1$

$A_{22} = (-1)^{2+2}\begin{vmatrix} 1 &2 \\ -2& 1 \end{vmatrix} =(1+4)= 5$

$A_{23} = (-1)^{2+3}\begin{vmatrix} 1 &-1 \\-2& 0 \end{vmatrix} =-(0-2)= 2$

$A_{31} = (-1)^{3+1}\begin{vmatrix} -1 &2 \\ 3& 5 \end{vmatrix} =(-5-6)= -11$

$A_{32} = (-1)^{3+2}\begin{vmatrix} 1 &2 \\2& 5\end{vmatrix} =-(5-4)= -1$

$A_{33} = (-1)^{3+3}\begin{vmatrix} 1 &-1 \\ 2& 3 \end{vmatrix} =(3+2)= 5$

Hence we get:

$adjA = \begin{bmatrix} A_{11} &A_{21} &A_{31} \\ A_{12}&A_{22} &A_{32} \\ A_{13}&A_{23} &A_{33} \end{bmatrix} = \begin{bmatrix} 3 &1 &-11 \\ -12&5 &-1 \\ 6&2 &5 \end{bmatrix}$

Question:3 Verify $\small A (adj A)=(adj A)A=|A|I$ .

$\small \begin{bmatrix} 2 &3 \\ -4 & -6 \end{bmatrix}$

Answer:

Given the matrix: $\small \begin{bmatrix} 2 &3 \\ -4 & -6 \end{bmatrix}$

Let $\small A = \begin{bmatrix} 2 &3 \\ -4 & -6 \end{bmatrix}$

Calculating the cofactors;

$\small A_{11} = (-1)^{1+1}(-6) = -6$

$\small A_{12} = (-1)^{1+2}(-4) = 4$

$\small A_{21} = (-1)^{2+1}(3) = -3$

$\small A_{22} = (-1)^{2+2}(2) = 2$

Hence, $\small adjA = \begin{bmatrix} -6 &-3 \\ 4& 2 \end{bmatrix}$

Now,

$\small A (adj A) = \begin{bmatrix} 2 &3 \\ -4&-6 \end{bmatrix}\left ( \begin{bmatrix} -6 &-3 \\ 4 &2 \end{bmatrix} \right )$

$\small \begin{bmatrix} -12+12 &-6+6 \\ 24-24 & 12-12 \end{bmatrix} = \begin{bmatrix} 0 &0 \\ 0 & 0 \end{bmatrix}$

aslo,

$\small (adjA)A = \begin{bmatrix} -6 &-3 \\ 4 & 2 \end{bmatrix}\begin{bmatrix} 2 &3 \\ -4& -6 \end{bmatrix}$

$\small = \begin{bmatrix} -12+12 &-18+18 \\ 8-8 & 12-12 \end{bmatrix} = \begin{bmatrix} 0 &0 \\ 0& 0 \end{bmatrix}$

Now, calculating |A|;

$\small |A| = -12-(-12) = -12+12 = 0$

So, $\small |A|I = 0\begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix} = \begin{bmatrix} 0 &0 \\ 0& 0 \end{bmatrix}$

Hence we get

$\small A (adj A)=(adj A)A=|A|I$

Question:4 Verify $\small A (adj A)=(adjA)A=|A| I$ .

$\small \begin{bmatrix} 1 &-1 & 2\\ 3 &0 &-2 \\ 1 & 0 &3 \end{bmatrix}$

Answer:

Given matrix: $\small \begin{bmatrix} 1 &-1 & 2\\ 3 &0 &-2 \\ 1 & 0 &3 \end{bmatrix}$

Let $\small A= \begin{bmatrix} 1 &-1 & 2\\ 3 &0 &-2 \\ 1 & 0 &3 \end{bmatrix}$

Calculating the cofactors;

$\small A_{11} = (-1)^{1+1} \begin{vmatrix} 0 &-2 \\ 0& 3 \end{vmatrix} = 0$

$\small A_{12} = (-1)^{1+2} \begin{vmatrix} 3 &-2 \\1& 3 \end{vmatrix} = -(9+2) =-11$

$\small A_{13} = (-1)^{1+3} \begin{vmatrix} 3 &0 \\ 1& 0 \end{vmatrix} = 0$

$\small A_{21} = (-1)^{2+1} \begin{vmatrix} -1 &2 \\ 0& 3 \end{vmatrix} = -(-3-0)= 3$

$\small A_{22} = (-1)^{2+2} \begin{vmatrix} 1 &2 \\ 1& 3 \end{vmatrix} = 3-2=1$

$\small A_{23} = (-1)^{2+3} \begin{vmatrix} 1 &-1 \\ 1& 0 \end{vmatrix} = -(0+1) = -1$

$\small A_{31} = (-1)^{3+1} \begin{vmatrix} -1 &2 \\ 0& -2 \end{vmatrix} = 2$

$\small A_{32} = (-1)^{3+2} \begin{vmatrix} 1 &2 \\ 3& -2 \end{vmatrix} = -(-2-6) = 8$

$\small A_{33} = (-1)^{3+3} \begin{vmatrix} 1 &-1 \\ 3& 0 \end{vmatrix} = 0+3 =3$

Hence, $\small adjA = \begin{bmatrix} 0 &3 &2 \\ -11 & 1& 8\\ 0 &-1 & 3 \end{bmatrix}$

Now,

$\small A (adj A) =\begin{bmatrix} 1 &-1 &2 \\ 3& 0 & -2\\ 1 & 0 & 3 \end{bmatrix}\begin{bmatrix} 0 &3 &2 \\ -11& 1& 8\\ 0& -1 &3 \end{bmatrix}$

$\small =\begin{bmatrix} 0+11+0 &3-1-2 &2-8+6 \\ 0+0+0 & 9+0+2 & 6+0-6 \\ 0+0+0 &3+0-3 & 2+0+9 \end{bmatrix} = \begin{bmatrix} 11 & 0 &0 \\ 0& 11&0 \\ 0 & 0 & 11 \end{bmatrix}$

also,

$\small A (adj A) =\begin{bmatrix} 0 &3 &2 \\ -11& 1& 8\\ 0& -1 &3 \end{bmatrix}\begin{bmatrix} 1 &-1 &2 \\ 3& 0 & -2\\ 1 & 0 & 3 \end{bmatrix}$

$\small =\begin{bmatrix} 0+9+2 &0+0+0 &0-6+6 \\ -11+3+8 & 11+0+0 & -22-2+24 \\ 0-3+3 &0+0+0 & 0+2+9 \end{bmatrix} = \begin{bmatrix} 11 & 0 &0 \\ 0& 11&0 \\ 0 & 0 & 11 \end{bmatrix}$

Now, calculating |A|;

$\small |A| = 1(0-0) +1(9+2) +2(0-0) = 11$

So, $\small |A|I = 11\begin{bmatrix} 1 &0&0 \\ 0& 1&0 \\ 0&0&1 \end{bmatrix} = \begin{bmatrix} 11 &0&0 \\ 0& 11&0\\ 0&0&11 \end{bmatrix}$

Hence we get,

$\small A (adj A)=(adj A)A=|A|I$ .

Question:5 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 2 &-2 \\ 4 & 3 \end{bmatrix}$

Answer:

Given matrix : $\small \begin{bmatrix} 2 &-2 \\ 4 & 3 \end{bmatrix}$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

|A| = (6+8) = 14

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (3) = 3$

$A_{12} = (-1)^{1+2} (4) = -4$

$A_{21} = (-1)^{2+1} (-2) = 2$

$A_{22} = (-1)^{2+2} (2) = 2$

So, we have $adjA = \begin{bmatrix} 3 &2 \\ -4& 2 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$= \frac{1}{14}\begin{bmatrix} 3 &2 \\ -4& 2 \end{bmatrix} = \begin{bmatrix} \frac{3}{14} &\frac{1}{7} \\ \\ \frac{-2}{7} & \frac{1}{7} \end{bmatrix}$

Question:6 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} -1 &5 \\ -3 &2 \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} -1 &5 \\ -3 &2 \end{bmatrix} = A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

|A| = (-2+15) = 13

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (2) = 2$

$A_{12} = (-1)^{1+2} (-3) = 3$

$A_{21} = (-1)^{2+1} (5) =-5$

$A_{22} = (-1)^{2+2} (-1) = -1$

So, we have $adjA = \begin{bmatrix} 2 &-5 \\ 3& -1 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$= \frac{1}{13}\begin{bmatrix} 2 &-5 \\ 3& -1 \end{bmatrix} = \begin{bmatrix} \frac{2}{13} &\frac{-5}{13} \\ \\ \frac{3}{13} & \frac{-1}{13} \end{bmatrix}$

Question:7 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 1 &2 &3 \\ 0 &2 &4 \\ 0 &0 &5 \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} 1 &2 &3 \\ 0 &2 &4 \\ 0 &0 &5 \end{bmatrix}= A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

$|A| = 1(10-0)-2(0-0)+3(0-0) = 10$

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (10) = 10$ $A_{12} = (-1)^{1+2} (0) = 0$

$A_{13} = (-1)^{1+3} (0) =0$ $A_{21} = (-1)^{2+1} (10) = -10$

$A_{22} = (-1)^{2+2} (5-0) = 5$ $A_{23} = (-1)^{2+1} (0-0) = 0$

$A_{31} = (-1)^{3+1} (8-6) = 2$ $A_{32} = (-1)^{3+2} (4-0) =-4$

$A_{33} = (-1)^{3+3} (2-0) = 2$

So, we have $adjA = \begin{bmatrix} 10 &-10 &2 \\ 0& 5 &-4 \\ 0& 0 &2 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$= \frac{1}{10}\begin{bmatrix} 10 &-10 &2 \\ 0 & 5& -4\\ 0 &0 &2 \end{bmatrix}$

Question:8 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 1 &0 &0 \\ 3 &3 &0 \\ 5 &2 &-1 \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} 1 &0 &0 \\ 3 &3 &0 \\ 5 &2 &-1 \end{bmatrix} = A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

$|A| = 1(-3-0)-0(-3-0)+0(6-15) = -3$

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (-3-0) = -3$ $A_{12} = (-1)^{1+2} (-3-0) = 3$

$A_{13} = (-1)^{1+3} (6-15) =-9$ $A_{21} = (-1)^{2+1} (0-0) = 0$

$A_{22} = (-1)^{2+2} (-1-0) = -1$ $A_{23} = (-1)^{2+1} (2-0) = -2$

$A_{31} = (-1)^{3+1} (0-0) = 0$ $A_{32} = (-1)^{3+2} (0-0) =0$

$A_{33} = (-1)^{3+3} (3-0) = 3$

So, we have $adjA = \begin{bmatrix} -3 &0 &0 \\ 3& -1 &0 \\ -9& -2 &3 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$= \frac{-1}{3}\begin{bmatrix} -3 &0 &0 \\ 3 & -1& 0\\ -9 &-2 &3 \end{bmatrix}$

Question:9 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 2 &1 &3 \\ 4 &-1 &0 \\ -7 &2 &1 \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} 2 &1 &3 \\ 4 &-1 &0 \\ -7 &2 &1 \end{bmatrix} =A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

$|A| = 2(-1-0)-1(4-0)+3(8-7) =-2-4+3 = -3$

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (-1-0) = -1$ $A_{12} = (-1)^{1+2} (4-0) = -4$

$A_{13} = (-1)^{1+3} (8-7) =1$ $A_{21} = (-1)^{2+1} (1-6) = 5$

$A_{22} = (-1)^{2+2} (2+21) = 23$ $A_{23} = (-1)^{2+1} (4+7) = -11$

$A_{31} = (-1)^{3+1} (0+3) = 3$ $A_{32} = (-1)^{3+2} (0-12) =12$

$A_{33} = (-1)^{3+3} (-2-4) = -6$

So, we have $adjA = \begin{bmatrix} -1 &5 &3 \\ -4& 23 &12 \\ 1& -11 &-6 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$A^{-1} = \frac{1}{-3} \begin{bmatrix} -1 &5 &3 \\ -4& 23 &12 \\ 1& -11 &-6 \end{bmatrix}$

Question:10 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 1 & -1 & 2\\ 0 & 2 &-3 \\ 3 &-2 &4 \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} 1 & -1 & 2\\ 0 & 2 &-3 \\ 3 &-2 &4 \end{bmatrix} = A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

$|A| = 1(8-6)+1(0+9)+2(0-6) =2+9-12 = -1$

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (8-6) = 2$ $A_{12} = (-1)^{1+2} (0+9) = -9$

$A_{13} = (-1)^{1+3} (0-6) =-6$ $A_{21} = (-1)^{2+1} (-4+4) = 0$

$A_{22} = (-1)^{2+2} (4-6) = -2$ $A_{23} = (-1)^{2+1} (-2+3) = -1$

$A_{31} = (-1)^{3+1} (3-4) = -1$ $A_{32} = (-1)^{3+2} (-3-0) =3$

$A_{33} = (-1)^{3+3} (2-0) = 2$

So, we have $adjA = \begin{bmatrix} 2 &0 &-1 \\ -9& -2 &3 \\ -6& -1 &2 \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$A^{-1} = \frac{1}{-1} \begin{bmatrix} 2 &0 &-1 \\ -9& -2 &3 \\ -6& -1 &2 \end{bmatrix}$

$A^{-1} = \begin{bmatrix} -2 &0 &1 \\ 9& 2 &-3 \\ 6& 1 &-2 \end{bmatrix}$

Question:11 Find the inverse of each of the matrices (if it exists).

$\small \begin{bmatrix} 1 & 0&0 \\ 0 &\cos \alpha &\sin \alpha \\ 0 &\sin \alpha &-\cos \alpha \end{bmatrix}$

Answer:

Given the matrix : $\small \begin{bmatrix} 1 & 0&0 \\ 0 &\cos \alpha &\sin \alpha \\ 0 &\sin \alpha &-\cos \alpha \end{bmatrix} =A$

To find the inverse we have to first find adjA then as we know the relation:

$A^{-1} = \frac{1}{|A|}adjA$

So, calculating |A| :

$|A| = 1(-\cos^2 \alpha-\sin^2 \alpha)+0(0-0)+0(0-0)$

$=-(\cos^2 \alpha + \sin^2 \alpha) = -1$

Now, calculating the cofactors terms and then adjA.

$A_{11} = (-1)^{1+1} (-\cos^2 \alpha - \sin^2 \alpha) = -1$ $A_{12} = (-1)^{1+2} (0-0) = 0$

$A_{13} = (-1)^{1+3} (0-0) =0$ $A_{21} = (-1)^{2+1} (0-0) = 0$

$A_{22} = (-1)^{2+2} (-\cos \alpha-0) = -\cos \alpha$ $A_{23} = (-1)^{2+1} (\sin \alpha-0) = -\sin \alpha$

$A_{31} = (-1)^{3+1} (0-0) = 0$ $A_{32} = (-1)^{3+2} (\sin \alpha-0) =-\sin \alpha$

$A_{33} = (-1)^{3+3} (\cos \alpha - 0) = \cos \alpha$

So, we have $adjA = \begin{bmatrix} -1 &0 &0 \\ 0& -\cos \alpha &-\sin \alpha \\ 0& -\sin \alpha &\cos \alpha \end{bmatrix}$

Therefore inverse of A will be:

$A^{-1} = \frac{1}{|A|}adjA$

$A^{-1} = \frac{1}{-1}\begin{bmatrix} -1 &0 &0 \\ 0& -\cos \alpha &-\sin \alpha \\ 0& -\sin \alpha &\cos \alpha \end{bmatrix} = \begin{bmatrix}1 &0 &0 \\ 0&\cos \alpha &\sin \alpha \\ 0& \sin \alpha &-\cos \alpha \end{bmatrix}$

Question:12 Let $\small A=\begin{bmatrix} 3 &7 \\ 2 & 5 \end{bmatrix}$ and $\small B=\begin{bmatrix} 6 &8 \\ 7 & 9 \end{bmatrix}$ . Verify that $\small (AB)^-^1=B^{-1}A^{-1}$ .

Answer:

We have $\small A=\begin{bmatrix} 3 &7 \\ 2 & 5 \end{bmatrix}$ and $\small B=\begin{bmatrix} 6 &8 \\ 7 & 9 \end{bmatrix}$ .

then calculating;

$AB = \begin{bmatrix} 3 &7 \\ 2& 5 \end{bmatrix}\begin{bmatrix} 6 &8 \\ 7& 9 \end{bmatrix}$

$=\begin{bmatrix} 18+49 &24+63 \\ 12+35 & 16+45 \end{bmatrix} = \begin{bmatrix} 67 &87 \\ 47& 61 \end{bmatrix}$

Finding the inverse of AB.

Calculating the cofactors fo AB:

$AB_{11}=(-1)^{1+1}(61) = 61$ $AB_{12}=(-1)^{1+2}(47) = -47$

$AB_{21}=(-1)^{2+1}(87) = -87$ $AB_{22}=(-1)^{2+2}(67) = 67$

Then we have adj(AB):

$adj(AB) = \begin{bmatrix} 61 &-87 \\ -47& 67 \end{bmatrix}$

and |AB| = 61(67) - (-87)(-47) = 4087-4089 = -2

Therefore we have inverse:

$(AB)^{-1}=\frac{1}{|AB|}adj(AB) = -\frac{1}{2} \begin{bmatrix} 61 &-87 \\ -47 & 67 \end{bmatrix}$

$= \begin{bmatrix} \frac{-61}{2} &\frac{87}{2} \\ \\ \frac{47}{2} & \frac{-67}{2} \end{bmatrix}$ .....................................(1)

Now, calculating inverses of A and B.

|A| = 15-14 = 1 and |B| = 54- 56 = -2

$adjA = \begin{bmatrix} 5 &-7 \\ -2 & 3 \end{bmatrix}$ and $adjB = \begin{bmatrix} 9 &-8 \\ -7 & 6 \end{bmatrix}$

therefore we have

$A^{-1} = \frac{1}{|A|}adjA= \frac{1}{1} \begin{bmatrix} 5&-7 \\ -2& 3 \end{bmatrix}$ and $B^{-1} = \frac{1}{|B|}adjB= \frac{1}{-2} \begin{bmatrix} 9&-8 \\ -7& 6 \end{bmatrix}= \begin{bmatrix} \frac{-9}{2} & 4 \\ \\ \frac{7}{2} & -3 \end{bmatrix}$

Now calculating $B^{-1}A^{-1}$ .

$B^{-1}A^{-1} =\begin{bmatrix} \frac{-9}{2} & 4 \\ \\ \frac{7}{2} & -3 \end{bmatrix}\begin{bmatrix} 5&-7 \\ -2& 3 \end{bmatrix}$

$=\begin{bmatrix} \frac{-45}{2}-8 && \frac{63}{2}+12 \\ \\ \frac{35}{2}+6 && \frac{-49}{2}-9 \end{bmatrix} = \begin{bmatrix} \frac{-61}{2} && \frac{87}{2} \\ \\ \frac{47}{2} && \frac{-67}{2} \end{bmatrix}$ ........................(2)

From (1) and (2) we get

$\small (AB)^-^1=B^{-1}A^{-1}$

Hence proved.

Question:13 If $\small A=\begin{bmatrix} 3 &1 \\ -1 &2 \end{bmatrix}$ ? , show that $A^2-5A+7I=O$ . Hence find $\small A^-^1$

Answer:

Given $\small A=\begin{bmatrix} 3 &1 \\ -1 &2 \end{bmatrix}$ then we have to show the relation $A^2-5A+7I=0$

So, calculating each term;

$A^2 = \begin{bmatrix} 3& 1\\ -1& 2 \end{bmatrix}\begin{bmatrix} 3&1 \\ -1& 2 \end{bmatrix} = \begin{bmatrix} 9-1 &3+2 \\ -3-2&-1+4 \end{bmatrix} = \begin{bmatrix} 8 &5 \\ -5& 3 \end{bmatrix}$

therefore $A^2-5A+7I$ ;

$=\begin{bmatrix} 8 &5 \\ -5& 3 \end{bmatrix} - 5\begin{bmatrix} 3 &1 \\ -1& 2 \end{bmatrix} + 7 \begin{bmatrix} 1 &0 \\ 0 & 1 \end{bmatrix}$

$=\begin{bmatrix} 8 &5 \\ -5& 3 \end{bmatrix} - \begin{bmatrix} 15 &5 \\ -5& 10 \end{bmatrix} + \begin{bmatrix} 7 &0 \\ 0 & 7 \end{bmatrix}$

$\begin{bmatrix} 8-15+7 &&5-5+0 \\ -5+5+0 && 3-10+7 \end{bmatrix} = \begin{bmatrix} 0 &&0 \\ 0 && 0 \end{bmatrix}$

Hence $A^2-5A+7I = 0$ .

$\therefore A.A -5A = -7I$

$\Rightarrow A.A(A^{-1}) - 5AA^{-1} = -7IA^{-1}$

[ Post multiplying by $A^{-1}$ , also $|A| \neq 0$ ]

$\Rightarrow A(AA^{-1}) - 5I = -7A^{-1}$

$\Rightarrow AI - 5I = -7A^{-1}$

$\Rightarrow -\frac{1}{7}(AI - 5I)= \frac{1}{7}(5I-A)$

$\therefore A^{-1} = \frac{1}{7}(5\begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix}-\begin{bmatrix} 3 &1 \\ -1& 2 \end{bmatrix}) = \frac{1}{7}\begin{bmatrix} 2 &-1 \\ 1& 3 \end{bmatrix}$

Question:14 For the matrix $\small A=\begin{bmatrix} 3 &2 \\ 1 & 1 \end{bmatrix}$ , find the numbers $\small a$ and $\small b$ such that $A^2+aA+bI=0$ .

Answer:

Given $\small A=\begin{bmatrix} 3 &2 \\ 1 & 1 \end{bmatrix}$ then we have the relation $A^2+aA+bI=O$

So, calculating each term;

$A^2 = \begin{bmatrix} 3& 2\\ 1& 1 \end{bmatrix}\begin{bmatrix} 3&2 \\ 1& 1 \end{bmatrix} = \begin{bmatrix} 9+2 &6+2 \\ 3+1&2+1 \end{bmatrix} = \begin{bmatrix} 11 &8 \\ 4& 3 \end{bmatrix}$

therefore $A^2+aA+bI=O$ ;

$=\begin{bmatrix}11 &8 \\ 4& 3 \end{bmatrix} + a\begin{bmatrix} 3 &2 \\ 1& 1 \end{bmatrix} + b \begin{bmatrix} 1 &0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 &0 \\ 0& 0 \end{bmatrix}$

$\begin{bmatrix} 11+3a+b & 8+2a \\ 4+a & 3+a+b \end{bmatrix} = \begin{bmatrix} 0 &0 \\ 0 & 0 \end{bmatrix}$

So, we have equations;

$11+3a+b = 0,\ 8+2a = 0$ and $4+a = 0,and\ \ 3+a+b = 0$

We get $a = -4\ and\ b= 1$ .

Question:15 For the matrix $\small A=\begin{bmatrix} 1 &1 &1 \\ 1 &2 &-3 \\ 2 &-1 &3 \end{bmatrix}$ Show that $\small A^3-6A^2+5A+11I=O$ Hence, find $\small A^-^1$ .

Answer:

Given matrix: $\small A=\begin{bmatrix} 1 &1 &1 \\ 1 &2 &-3 \\ 2 &-1 &3 \end{bmatrix}$ ;

To show: $\small A^3-6A^2+5A+11I=O$

Finding each term:

$A^{2} = \begin{bmatrix} 1 & 1& 1\\ 1 & 2& -3\\ 2& -1 & 3 \end{bmatrix} \begin{bmatrix} 1 & 1& 1\\ 1 & 2& -3\\ 2& -1 & 3 \end{bmatrix}$

$= \begin{bmatrix} 1+1+2 &&1+2-1 &&1-3+3 \\ 1+2-6 &&1+4+3 &&1-6-9 \\ 2-1+6 &&2-2-3 && 2+3+9 \end{bmatrix}$

$= \begin{bmatrix} 4 &&2 &&1 \\ -3 &&8 &&-14 \\ 7 &&-3 && 14 \end{bmatrix}$

$A^{3} = \begin{bmatrix} 4 &&2 &&1 \\ -3 &&8 &&-14 \\ 7 &&-3 && 14 \end{bmatrix}\begin{bmatrix} 1 &1 &1 \\ 1 &2 &-3 \\ 2 &-1 &3 \end{bmatrix}$

$= \begin{bmatrix} 4+2+2 &4+4-1 &4-6+3 \\ -3+8-28 &-3+16+14 & -3-24-42 \\ 7-3+28&7-6-14 &7+9+42 \end{bmatrix}$

$= \begin{bmatrix} 8 &7 &1 \\ -23 &27 & -69 \\ 32&-13 &58 \end{bmatrix}$

So now we have, $\small A^3-6A^2+5A+11I$

$= \begin{bmatrix} 8 &7 &1 \\ -23 &27 & -69 \\ 32&-13 &58 \end{bmatrix}-6\begin{bmatrix} 4 &&2 &&1 \\ -3 &&8 &&-14 \\ 7 &&-3 && 14 \end{bmatrix}+5\begin{bmatrix} 1 &1 &1 \\ 1 &2 &-3 \\ 2 &-1 &3 \end{bmatrix}+11\begin{bmatrix} 1 &0 &0 \\ 0 &1 & 0\\ 0& 0& 1 \end{bmatrix}$

$= \begin{bmatrix} 8 &7 &1 \\ -23 &27 & -69 \\ 32&-13 &58 \end{bmatrix}-\begin{bmatrix} 24 &&12 &&6 \\ -18 &&48 &&-84 \\ 42 &&-18 && 84 \end{bmatrix}+\begin{bmatrix} 5 &5 &5 \\ 5 &10 &-15 \\ 10 &-5 &15 \end{bmatrix}+\begin{bmatrix} 11 &0 &0 \\ 0 &11 & 0\\ 0& 0& 11 \end{bmatrix}$

$= \begin{bmatrix} 8-24+5+11 &7-12+5 &1-6+5 \\ -23+18+5&27-48+10+11 &-69+84-15 \\ 32-42+10&-13+18-5 & 58-84+15+11 \end{bmatrix}$

$= \begin{bmatrix} 0 &0 &0 \\ 0&0 &0 \\ 0&0 & 0 \end{bmatrix} = 0$

Now finding the inverse of A;

Post-multiplying by $A^{-1}$ as, $|A| \neq 0$

$\Rightarrow (AAA)A^{-1}-6(AA)A^{-1} +5AA^{-1}+11IA^{-1} = 0$

$\Rightarrow AA(AA^{-1})-6A(AA^{-1}) +5(AA^{-1})=- 11IA^{-1}$

$\Rightarrow A^{2}-6A +5I=- 11A^{-1}$

$A^{-1} = \frac{-1}{11}(A^{2}-6A+5I)$ ...................(1)

Now,

From equation (1) we get;

$A^{-1} = \frac{-1}{11}( \begin{bmatrix} 4 &&2 &&1 \\ -3 &&8 &&-14 \\ 7 &&-3 && 14 \end{bmatrix}-6\begin{bmatrix} 1 &1 &1 \\ 1 &2 &-3 \\ 2 &-1 &3 \end{bmatrix}+5\begin{bmatrix} 1 & 0& 0\\ 0&1 &0 \\ 0& 0&1 \end{bmatrix})$

$A^{-1} = \frac{-1}{11}( \begin{bmatrix} 4-6+5 &&2-6 &&1-6 \\ -3-6 &&8-12+5 &&-14+18 \\ 7-12 &&-3+6 && 14-18+5 \end{bmatrix}$

$A^{-1} = \frac{-1}{11}( \begin{bmatrix} 3 &&-4 &&-5 \\ -9 &&1 &&4 \\ -5 &&3 && 1 \end{bmatrix}$

Question:16 If $\small A=\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}$ , verify that $\small A^3-6A^2+9A-4I=O$ . Hence find $\small A^-^1$ .

Answer:

Given matrix: $\small A=\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}$ ;

To show: $\small A^3-6A^2+9A-4I$

Finding each term:

$A^{2} = \begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}$

$= \begin{bmatrix} 4+1+1 &&-2-2-1 &&2+1+2 \\ -2-2-1 &&1+4+1 &&-1-2-2 \\ 2+1+2 &&-1-2-2 && 1+1+4 \end{bmatrix}$

$= \begin{bmatrix} 6 &&-5 &&5 \\ -5 &&6 &&-5 \\ 5 &&-5 && 6 \end{bmatrix}$

$A^{3} =\begin{bmatrix} 6 &&-5 &&5 \\ -5 &&6 &&-5 \\ 5 &&-5 && 6 \end{bmatrix}\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}$

$= \begin{bmatrix} 12+5+5 &-6-10-5 &6+5+10 \\ -10-6-5 &5+12+5 & -5-6-10 \\ 10+5+6&-5-10-6 &5+5+12 \end{bmatrix}$

$= \begin{bmatrix} 22 &-21 &21 \\ -21 &22 & -21 \\ 21&-21 &22 \end{bmatrix}$

So now we have, $\small A^3-6A^2+9A-4I$

$=\begin{bmatrix} 22 &-21 &21 \\ -21 &22 & -21 \\ 21&-21 &22 \end{bmatrix}-6 \begin{bmatrix} 6 &&-5 &&5 \\ -5 &&6 &&-5 \\ 5 &&-5 && 6 \end{bmatrix}+9\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}-4\begin{bmatrix} 1 &0 &0 \\ 0 &1 & 0\\ 0& 0& 1 \end{bmatrix}$

$=\begin{bmatrix} 22 &-21 &21 \\ -21 &22 & -21 \\ 21&-21 &22 \end{bmatrix}- \begin{bmatrix} 36 &&-30 &&30 \\ -30 &&36 &&-30 \\30 &&-30 && 36 \end{bmatrix}+\begin{bmatrix} 18 &-9 &9 \\ -9 &18 &-9 \\ 9 &-9 &18 \end{bmatrix}-\begin{bmatrix} 4 &0 &0 \\ 0 &4 & 0\\ 0& 0& 4 \end{bmatrix}$

$= \begin{bmatrix} 22-36+18-4 &-21+30-9 &21-30+9 \\ -21+30-9&22-36+18-4 &-21+30-9 \\ 21-30+9&-21+30-9 & 22-36+18-4 \end{bmatrix}$

$= \begin{bmatrix} 0 &0 &0 \\ 0&0 &0 \\ 0&0 & 0 \end{bmatrix} = O$

Now finding the inverse of A;

Post-multiplying by $A^{-1}$ as, $|A| \neq 0$

$\Rightarrow (AAA)A^{-1}-6(AA)A^{-1} +9AA^{-1}-4IA^{-1} = 0$

$\Rightarrow AA(AA^{-1})-6A(AA^{-1}) +9(AA^{-1})=4IA^{-1}$

$\Rightarrow A^{2}-6A +9I=4A^{-1}$

$A^{-1} = \frac{1}{4}(A^{2}-6A+9I)$ ...................(1)

Now,

From equation (1) we get;

$A^{-1} = \frac{1}{4}(\begin{bmatrix} 6 &&-5 &&5 \\ -5 &&6 &&-5 \\ 5 &&-5 && 6 \end{bmatrix}-6\begin{bmatrix} 2 &-1 &1 \\ -1 &2 &-1 \\ 1 &-1 &2 \end{bmatrix}+9\begin{bmatrix} 1 & 0& 0\\ 0&1 &0 \\ 0& 0&1 \end{bmatrix})$

$A^{-1} = \frac{1}{4} \begin{bmatrix} 6-12+9 &&-5+6 &&5-6 \\ -5+6 &&6-12+9 &&-5+6 \\ 5-6 &&-5+6 && 6-12+9 \end{bmatrix}$

Hence inverse of A is :

$A^{-1} = \frac{1}{4} \begin{bmatrix} 3 &&1 &&-1 \\ 1 &&3 &&1 \\ -1 &&1 && 3 \end{bmatrix}$

Question:17 Let A be a nonsingular square matrix of order $\small 3\times 3$ . Then $\small |adjA|$ is equal to

(A) $\small |A|$ (B) $\small |A|^2$ (C) $\small |A|^3$ (D) $\small 3|A|$

Answer:

We know the identity $(adjA)A = |A| I$

Hence we can determine the value of $|(adjA)|$ .

Taking both sides determinant value we get,

$|(adjA)A| = ||A| I|$ or $|(adjA)||A| = ||A||| I|$

or taking R.H.S.,

$||A||| I| = \begin{vmatrix} |A| & 0&0 \\ 0&|A| &0 \\ 0&0 &|A| \end{vmatrix}$

$= |A| (|A|^2) = |A|^3$

or, we have then $|(adjA)||A| = |A|^3$

Therefore $|(adjA)| = |A|^2$

Hence the correct answer is B.

Question:18 If A is an invertible matrix of order 2, then det $\small (A^-^1)$ is equal to

(A) $\small det(A)$ (B) $\small \frac{1}{det (A)}$ (C) $\small 1$ (D) $\small 0$

Answer:

Given that the matrix is invertible hence $A^{-1}$ exists and $A^{-1} = \frac{1}{|A|}adjA$

Let us assume a matrix of the order of 2;

$A = \begin{bmatrix} a &b \\ c &d \end{bmatrix}$ .

Then $|A| = ad-bc$ .

$adjA = \begin{bmatrix} d &-b \\ -c & a \end{bmatrix}$ and $|adjA| = ad-bc$

Now,

$A^{-1} = \frac{1}{|A|}adjA$

Taking determinant both sides;

$|A^{-1}| = |\frac{1}{|A|}adjA| = \begin{bmatrix} \frac{d}{|A|} &\frac{-b}{|A|} \\ \\ \frac{-c}{|A|} & \frac{a}{|A|} \end{bmatrix}$

$\therefore|A^{-1}| = \begin{vmatrix} \frac{d}{|A|} &\frac{-b}{|A|} \\ \\ \frac{-c}{|A|} & \frac{a}{|A|} \end{vmatrix} = \frac{1}{|A|^2}\begin{vmatrix} d &-b \\ -c& a \end{vmatrix} = \frac{1}{|A|^2}(ad-bc) =\frac{1}{|A|^2}.|A| = \frac{1}{|A|}$

Therefore we get;

$|A^{-1}| = \frac{1}{|A|}$

Hence the correct answer is B.

NCERT determinants class 12 ncert solutions: Excercise- 4.6

Question:1 Examine the consistency of the system of equations.

$\small x+2y=2$

$\small 2x+3y=3$

Answer:

We have given the system of equations:18967

$\small x+2y=2$

$\small 2x+3y=3$

The given system of equations can be written in the form of the matrix; $AX =B$

where $A= \begin{bmatrix} 1 &2 \\ 2&3 \end{bmatrix}$ , $X= \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 2\\3 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 1(3) -2(2) = -1 \neq 0$

Here A is non -singular therefore there exists $A^{-1}$ .

Hence, the given system of equations is consistent.

Question:2 Examine the consistency of the system of equations

$\small 2x-y=5$

$\small x+y=4$

Answer:

We have given the system of equations:

$\small 2x-y=5$

$\small x+y=4$

The given system of equations can be written in the form of matrix; $AX =B$

where $A= \begin{bmatrix} 2 &-1 \\ 1&1 \end{bmatrix}$ , $X= \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 5\\4 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 2(1) -1(-1) = 3 \neq 0$

Here A is non -singular therefore there exists $A^{-1}$ .

Hence, the given system of equations is consistent.

Question:3 Examine the consistency of the system of equations.

$\small x+3y=5$

$\small 2x+6y=8$

Answer:

We have given the system of equations:

$\small x+3y=5$

$\small 2x+6y=8$

The given system of equations can be written in the form of the matrix; $AX =B$

where $A= \begin{bmatrix} 1 &3 \\ 2&6 \end{bmatrix}$ , $X= \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 5\\8 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 1(6) -2(3) = 0$

Here A is singular matrix therefore now we will check whether the $(adjA)B$ is zero or non-zero.

$adjA= \begin{bmatrix} 6 &-3 \\ -2& 1 \end{bmatrix}$

So, $(adjA)B= \begin{bmatrix} 6 &-3 \\ -2& 1 \end{bmatrix}\begin{bmatrix} 5\\8 \end{bmatrix} = \begin{bmatrix} 30-24\\-10+8 \end{bmatrix}=\begin{bmatrix} 6\\-2 \end{bmatrix} \neq 0$

As, $(adjA)B \neq 0$ , the solution of the given system of equations does not exist.

Hence, the given system of equations is inconsistent.

Question:4 Examine the consistency of the system of equations.

$\small x+y+z=1$

$\small 2x+3y+2z=2$

$\small ax+ay+2az=4$

Answer:

We have given the system of equations:

$\small x+y+z=1$

$\small 2x+3y+2z=2$

$\small ax+ay+2az=4$

The given system of equations can be written in the form of the matrix; $AX =B$

where $A = \begin{bmatrix} 1& 1&1 \\ 2& 3& 2\\ a& a &2a \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\ z \end{bmatrix}$ and $B = \begin{bmatrix} 1\\2 \\ 4 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 1(6a-2a) -1(4a-2a)+1(2a-3a)$

$= 4a -2a-a = 4a -3a =a \neq 0$

[ If zero then it won't satisfy the third equation ]

Here A is non- singular matrix therefore there exist $A^{-1}$ .

Hence, the given system of equations is consistent.

Question:5 Examine the consistency of the system of equations.

$\small 3x-y-2z=2$

$\small 2y-z=-1$

$\small 3x-5y=3$

Answer:

We have given the system of equations:

$\small 3x-y-2z=2$

$\small 2y-z=-1$

$\small 3x-5y=3$

The given system of equations can be written in the form of matrix; $AX =B$

where $A = \begin{bmatrix} 3& -1&-2 \\ 0& 2& -1\\ 3& -5 &0 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\ z \end{bmatrix}$ and $B = \begin{bmatrix} 2\\-1 \\ 3 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 3(0-5) -(-1)(0+3)-2(0-6)$

$= -15 +3+12 = 0$

Therefore matrix A is a singular matrix.

So, we will then check $(adjA)B,$

$(adjA) = \begin{bmatrix} -5 &10 &5 \\ -3& 6 & 3\\ -6& 12 & 6 \end{bmatrix}$

$\therefore (adjA)B = \begin{bmatrix} -5 &10 &5 \\ -3& 6 & 3\\ -6& 12 & 6 \end{bmatrix}\begin{bmatrix} 2\\-1 \\ 3 \end{bmatrix} = \begin{bmatrix} -10-10+15\\ -6-6+9 \\ -12-12+18 \end{bmatrix} = \begin{bmatrix} -5\\-3 \\ -6 \end{bmatrix} \neq 0$

As, $(adjA)B$ is non-zero thus the solution of the given system of the equation does not exist. Hence, the given system of equations is inconsistent.

Question:6 Examine the consistency of the system of equations.

$\small 5x-y+4z=5$

$\small 2x+3y+5z=2$

$\small 5x-2y+6z=-1$

Answer:

We have given the system of equations:

$\small 5x-y+4z=5$

$\small 2x+3y+5z=2$

$\small 5x-2y+6z=-1$

The given system of equations can be written in the form of the matrix; $AX =B$

where $A = \begin{bmatrix} 5& -1&4 \\ 2& 3& 5\\ 5& -2 &6 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\ z \end{bmatrix}$ and $B = \begin{bmatrix} 5\\2 \\ -1 \end{bmatrix}$ .

So, we want to check for the consistency of the equations;

$|A| = 5(18+10) +1(12-25)+4(-4-15)$

$= 140-13-76 = 51 \neq 0$

Here A is non- singular matrix therefore there exist $A^{-1}$ .

Hence, the given system of equations is consistent.

Question:7 Solve system of linear equations, using matrix method.

$\small 5x+2y=4$

$\small 7x+3y=5$

Answer:

The given system of equations

$\small 5x+2y=4$

$\small 7x+3y=5$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 5 &4 \\ 7& 3 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 4\\5 \end{bmatrix}$

we have,

$|A| = 15-14=1 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

$A^{-1} = \frac{1}{|A|} (adjA) = (adjA) = \begin{bmatrix} 3 &-2 \\ -7& 5 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \begin{bmatrix} 3 &-2 \\ -7 & 5 \end{bmatrix}\begin{bmatrix} 4\\5 \end{bmatrix}$

$\Rightarrow \begin{bmatrix} x\\y \end{bmatrix} = \begin{bmatrix} 12-10\\ -28+25 \end{bmatrix} = \begin{bmatrix} 2\\-3 \end{bmatrix}$

Hence the solutions of the given system of equations;

x = 2 and y =-3 .

Question:8 Solve system of linear equations, using matrix method.

$2x-y=-2$

$3x+4y=3$

Answer:

The given system of equations

$2x-y=-2$

$3x+4y=3$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 2 &-1 \\ 3& 4 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} -2\\3 \end{bmatrix}$

we have,

$|A| = 8+3=11 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{11}\begin{bmatrix} 4 &1 \\ -3& 2 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \frac{1}{11}\begin{bmatrix} 4 &1 \\ -3 & 2 \end{bmatrix}\begin{bmatrix} -2\\3 \end{bmatrix}$

$\Rightarrow \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{11}\begin{bmatrix} -8+3\\ 6+6 \end{bmatrix} = \frac{1}{11}\begin{bmatrix} -5\\12 \end{bmatrix}= \begin{bmatrix} -\frac{5}{11}\\ \\-\frac{12}{11} \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =\frac{-5}{11} \ and\ y =\frac{12}{11}.$

Question:9 Solve system of linear equations, using matrix method.

$\small 4x-3y=3$

$\small 3x-5y=7$

Answer:

The given system of equations

$\small 4x-3y=3$

$\small 3x-5y=7$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 4 &-3 \\ 3& -5 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 3\\7 \end{bmatrix}$

we have,

$|A| = -20+9=-11 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{-1}{11}\begin{bmatrix} -5 &3 \\ -3& 4 \end{bmatrix} = \frac{1}{11} \begin{bmatrix} 5 &-3 \\ 3& -4 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \frac{1}{11}\begin{bmatrix} 5 &-3 \\ 3 & -4 \end{bmatrix}\begin{bmatrix} 3\\7 \end{bmatrix}$

$\Rightarrow \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{11}\begin{bmatrix} 15-21\\ 9-28 \end{bmatrix} = \frac{1}{11}\begin{bmatrix} -6\\-19 \end{bmatrix}= \begin{bmatrix} -\frac{6}{11}\\ \\-\frac{19}{11} \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =\frac{-6}{11} \ and\ y =\frac{-19}{11}.$

Question:10 Solve system of linear equations, using matrix method.

$\small 5x+2y=3$

$\small 3x+2y=5$

Answer:

The given system of equations

$\small 5x+2y=3$

$\small 3x+2y=5$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 5 &2 \\ 3& 2 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \end{bmatrix}$ and $B = \begin{bmatrix} 3\\5 \end{bmatrix}$

we have,

$|A| = 10-6=4 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{4}\begin{bmatrix} 2 &-2 \\ -3& 5 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \frac{1}{4}\begin{bmatrix} 2 &-2 \\ -3 & 5 \end{bmatrix}\begin{bmatrix} 3\\5 \end{bmatrix}$

$\Rightarrow \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{4}\begin{bmatrix} 6-10\\ -9+25 \end{bmatrix} = \frac{1}{4}\begin{bmatrix} -4\\16 \end{bmatrix}= \begin{bmatrix} -1\\4 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =-1 \ and\ y =4.$

Question:11 Solve system of linear equations, using matrix method.

$\small 2x+y+z=1$

$\small x-2y-z= \frac{3}{2}$

$\small 3y-5z=9$

Answer:

The given system of equations

$\small 2x+y+z=1$

$\small x-2y-z= \frac{3}{2}$

$\small 3y-5z=9$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 2 &1 &1 \\ 1 & -2 &-1 \\ 0& 3 &-5 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\z \end{bmatrix}$ and $B =\begin{bmatrix} 1\\ \\ \frac{3}{2} \\ \\ 9 \end{bmatrix}$

we have,

$|A| =2(10+3)-1(-5-0)+1(3-0) = 26+5+3 = 34 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

Now, we will find the cofactors;

$A_{11} =(-1)^{1+1}(10+3) = 13$ $A_{12} =(-1)^{1+2}(-5-0) = 5$

$A_{13} =(-1)^{1+3}(3-0) = 3$ $A_{21} =(-1)^{2+1}(-5-3) = 8$

$A_{22} =(-1)^{2+2}(-10-0) = -10$ $A_{23} =(-1)^{2+3}(6-0) = -6$

$A_{31} =(-1)^{3+1}(-1+2) = 1$ $A_{32} =(-1)^{3+2}(-2-1) = 3$

$A_{33} =(-1)^{3+3}(-4-1) = -5$

$(adjA) =\begin{bmatrix} 13 &8 &1 \\ 5& -10 & 3\\ 3& -6 & -5 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{34}\begin{bmatrix} 13 &8 &1 \\ 5& -10 & 3\\ 3& -6 & -5 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \frac{1}{34}\begin{bmatrix} 13 &8 &1 \\ 5& -10 & 3\\ 3& -6 & -5 \end{bmatrix}\begin{bmatrix} 1\\\frac{3}{2} \\ 9 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \frac{1}{34}\begin{bmatrix} 13+12+9\\5-15+27 \\ 3-9-45 \end{bmatrix} = \frac{1}{34}\begin{bmatrix} 34\\17 \\ -51 \end{bmatrix}= \begin{bmatrix} 1\\\frac{1}{2} \\ -\frac{3}{2} \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =1,\ y =\frac{1}{2},\ and\ \ z=-\frac{3}{2}.$

Question:12 Solve system of linear equations, using matrix method.

$\small x-y+z=4$

$\small 2x+y-3z=0$

$\small x+y+z=2$

Answer:

The given system of equations

$\small x-y+z=4$

$\small 2x+y-3z=0$

$\small x+y+z=2$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 1 &-1 &1 \\ 2 & 1 &-3 \\ 1& 1 &1 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\z \end{bmatrix}$ $and\ B =\begin{bmatrix} 4\\ 0 \\ 2 \end{bmatrix}.$

we have,

$|A| =1(1+3)+1(2+3)+1(2-1) = 4+5+1= 10 \neq 0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

Now, we will find the cofactors;

$A_{11} =(-1)^{1+1}(1+3) = 4$ $A_{12} =(-1)^{1+2}(2+3) = -5$

$A_{13} =(-1)^{1+3}(2-1) = 1$ $A_{21} =(-1)^{2+1}(-1-1) = 2$

$A_{22} =(-1)^{2+2}(1-1) = 0$ $A_{23} =(-1)^{2+3}(1+1) = -2$

$A_{31} =(-1)^{3+1}(3-1) = 2$ $A_{32} =(-1)^{3+2}(-3-2) = 5$

$A_{33} =(-1)^{3+3}(1+2) = 3$

$(adjA) =\begin{bmatrix} 4 &2 &2 \\ -5& 0 & 5\\ 1& -2 & 3 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{10}\begin{bmatrix} 4 &2 &2 \\ -5& 0 & 5\\ 1& -2 & 3 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B =\frac{1}{10}\begin{bmatrix} 4 &2 &2 \\ -5& 0 & 5\\ 1& -2 & 3 \end{bmatrix}\begin{bmatrix} 4\\0 \\ 2 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \frac{1}{10}\begin{bmatrix} 16+0+4\\-20+0+10 \\ 4+0+6 \end{bmatrix} = \frac{1}{10}\begin{bmatrix} 20\\-10 \\ 10 \end{bmatrix}= \begin{bmatrix} 2\\-1 \\ 1 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =2,\ y =-1,\ and\ \ z=1.$

Question:13 Solve system of linear equations, using matrix method.

$\small 2x+3y+3z=5$

$\small x-2y+z=-4$

$\small 3x-y-2z=3$

Answer:

The given system of equations

$\small 2x+3y+3z=5$

$\small x-2y+z=-4$

$\small 3x-y-2z=3$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 2 &3 &3 \\ 1 & -2 &1 \\ 3& -1 &-2 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\z \end{bmatrix}$ $and\ B =\begin{bmatrix} 5\\ -4 \\ 3 \end{bmatrix}.$

we have,

$|A| =2(4+1) -3(-2-3)+3(-1+6) = 10+15+15 = 40$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

Now, we will find the cofactors;

$A_{11} =(-1)^{1+1}(4+1) = 5$ $A_{12} =(-1)^{1+2}(-2-3) = 5$

$A_{13} =(-1)^{1+3}(-1+6) = 5$ $A_{21} =(-1)^{2+1}(-6+3) = 3$

$A_{22} =(-1)^{2+2}(-4-9) = -13$ $A_{23} =(-1)^{2+3}(-2-9) = 11$

$A_{31} =(-1)^{3+1}(3+6) = 9$ $A_{32} =(-1)^{3+2}(2-3) = 1$

$A_{33} =(-1)^{3+3}(-4-3) = -7$

$(adjA) =\begin{bmatrix} 5 &3 &9 \\ 5& -13 & 1\\ 5&11 & -7 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{40}\begin{bmatrix} 5 &3 &9 \\ 5& -13 & 1\\ 5& 11 & -7 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B =\frac{1}{40}\begin{bmatrix} 5 &3 &9 \\ 5& -13 & 1\\ 5& 11 & -7 \end{bmatrix}\begin{bmatrix} 5\\-4 \\ 3 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \frac{1}{40}\begin{bmatrix} 25-12+27\\25+52+3 \\ 25-44-21 \end{bmatrix} = \frac{1}{40}\begin{bmatrix} 40\\80 \\ -40 \end{bmatrix}= \begin{bmatrix} 1\\2 \\ -1 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =1,\ y =2,\ and\ \ z=-1.$

Question:14 Solve system of linear equations, using matrix method.

$\small x-y+2z=7$

$\small 3x+4y-5z=-5$

$\small 2x-y+3z=12$

Answer:

The given system of equations

$\small x-y+2z=7$

$\small 3x+4y-5z=-5$

$\small 2x-y+3z=12$

can be written in the matrix form of AX =B, where

$A = \begin{bmatrix} 1 &-1 &2 \\ 3 & 4 &-5 \\ 2& -1 &3 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\z \end{bmatrix}$ $and\ B =\begin{bmatrix} 7\\ -5 \\ 12 \end{bmatrix}.$

we have,

$|A| =1(12-5) +1(9+10)+2(-3-8) = 7+19-22 = 4 \neq0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

Now, we will find the cofactors;

$A_{11} =(-1)^{12-5} = 7$ $A_{12} =(-1)^{1+2}(9+10) = -19$

$A_{13} =(-1)^{1+3}(-3-8) = -11$ $A_{21} =(-1)^{2+1}(-3+2) = 1$

$A_{22} =(-1)^{2+2}(3-4) = -1$ $A_{23} =(-1)^{2+3}(-1+2) = -1$

$A_{31} =(-1)^{3+1}(5-8) = -3$ $A_{32} =(-1)^{3+2}(-5-6) = 11$

$A_{33} =(-1)^{3+3}(4+3) = 7$

$(adjA) =\begin{bmatrix} 7 &1 &-3 \\ -19& -1 & 11\\ -11&-1 & 7 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{4}\begin{bmatrix} 7 &1 &-3 \\ -19& -1 & 11\\ -11&-1 & 7 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B =\frac{1}{4}\begin{bmatrix} 7 &1 &-3 \\ -19& -1 & 11\\ -11&-1 & 7 \end{bmatrix}\begin{bmatrix} 7\\-5 \\ 12 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \frac{1}{4}\begin{bmatrix} 49-5-36\\-133+5+132 \\ -77+5+84 \end{bmatrix} = \frac{1}{4}\begin{bmatrix} 8\\4 \\ 12 \end{bmatrix}= \begin{bmatrix} 2\\1 \\ 3 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =2,\ y =1,\ and\ \ z=3.$

Question:15 If $A=\begin{bmatrix} 2 &-3 &5 \\ 3 & 2 &-4 \\ 1 &1 &-2 \end{bmatrix}$ , find $A^-^1$ . Using $A^-^1$ solve the system of equations

$2x-3y+5z=11$

$3x+2y-4z=-5$

$x+y-2z=-3$

Answer:

The given system of equations

$2x-3y+5z=11$

$3x+2y-4z=-5$

$x+y-2z=-3$

can be written in the matrix form of AX =B, where

$A=\begin{bmatrix} 2 &-3 &5 \\ 3 & 2 &-4 \\ 1 &1 &-2 \end{bmatrix}$ , $X = \begin{bmatrix} x\\y \\z \end{bmatrix}$ $and\ B =\begin{bmatrix} 11\\ -5 \\ -3 \end{bmatrix}.$

we have,

$|A| =2(-4+4) +3(-6+4)+5(3-2) = 0-6+5 = -1 \neq0$ .

So, A is non-singular, Therefore, its inverse $A^{-1}$ exists.

as we know $A^{-1} = \frac{1}{|A|} (adjA)$

Now, we will find the cofactors;

$A_{11} =(-1)^{-4+4} = 0$ $A_{12} =(-1)^{1+2}(-6+4) = 2$

$A_{13} =(-1)^{1+3}(3-2) = 1$ $A_{21} =(-1)^{2+1}(6-5) = -1$

$A_{22} =(-1)^{2+2}(-4-5) = -9$ $A_{23} =(-1)^{2+3}(2+3) = -5$

$A_{31} =(-1)^{3+1}(12-10) = 2$ $A_{32} =(-1)^{3+2}(-8-15) = 23$

$A_{33} =(-1)^{3+3}(4+9) = 13$

$(adjA) =\begin{bmatrix} 0 &-1 &2 \\ 2& -9 & 23\\ 1&-5 & 13 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = -1\begin{bmatrix} 0 &-1 &2 \\ 2& -9 & 23\\ 1&-5 & 13 \end{bmatrix} = \begin{bmatrix} 0 &1 &-2 \\ -2& 9 & -23\\ -1&5 & -13 \end{bmatrix}$

So, the solutions can be found by $X = A^{-1}B = \begin{bmatrix} 0 &1 &-2 \\ -2& 9 & -23\\ -1&5 & -13 \end{bmatrix}\begin{bmatrix} 11\\-5 \\ -3 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \begin{bmatrix} 0-5+6\\-22-45+69 \\ -11-25+39 \end{bmatrix} = \begin{bmatrix} 1\\2 \\ 3 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =1,\ y =2,\ and\ \ z=3.$

Question:16 The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by matrix method.

Answer:

So, let us assume the cost of onion, wheat, and rice be x , y and z respectively.

Then we have the equations for the given situation :

$4x+3y+2z = 60$

$2x+4y+6z = 90$

$6x+2y+3y = 70$

We can find the cost of each item per Kg by the matrix method as follows;

Taking the coefficients of x, y, and z as a matrix $A$ .

We have;

$A = \begin{bmatrix} 4 &3 &2 \\ 2& 4 &6 \\ 6 & 2 & 3 \end{bmatrix},$ $X= \begin{bmatrix} x\\y \\ z \end{bmatrix}$ $and\ B = \begin{bmatrix} 60\\90 \\ 70 \end{bmatrix}.$

$|A| = 4(12-12) -3(6-36)+2(4-24) = 0 +90-40 = 50 \neq 0$

Now, we will find the cofactors of A;

$A_{11} = (-1)^{1+1}(12-12) = 0$ $A_{12} = (-1)^{1+2}(6-36) = 30$

$A_{13} = (-1)^{1+3}(4-24) = -20$ $A_{21} = (-1)^{2+1}(9-4) = -5$

$A_{22} = (-1)^{2+2}(12-12) = 0$ $A_{23} = (-1)^{2+3}(8-18) = 10$

$A_{31} = (-1)^{3+1}(18-8) = 10$ $A_{32} = (-1)^{3+2}(24-4) = -20$

$A_{33} = (-1)^{3+3}(16-6) = 10$

Now we have adjA;

$adjA = \begin{bmatrix} 0 &-5 &10 \\ 30 & 0 &-20 \\ -20 & 10 & 10 \end{bmatrix}$

$A^{-1} = \frac{1}{|A|} (adjA) = \frac{1}{50}\begin{bmatrix} 0 &-5 &10 \\ 30 & 0 &-20 \\ -20 & 10 & 10 \end{bmatrix}$ s

So, the solutions can be found by $X = A^{-1}B = \frac{1}{50}\begin{bmatrix} 0 &-5 &10 \\ 30 & 0 &-20 \\ -20 & 10 & 10 \end{bmatrix}\begin{bmatrix} 60\\90 \\ 70 \end{bmatrix}$

$\Rightarrow\begin{bmatrix} x\\y \\ z \end{bmatrix} = \begin{bmatrix} 0-450+700\\1800+0-1400 \\ -1200+900+700 \end{bmatrix} =\frac{1}{50} \begin{bmatrix} 250\\400 \\ 400 \end{bmatrix} = \begin{bmatrix} 5\\8 \\ 8 \end{bmatrix}$

Hence the solutions of the given system of equations;

$x =5,\ y =8,\ and\ \ z=8.$

Therefore, we have the cost of onions is Rs. 5 per Kg, the cost of wheat is Rs. 8 per Kg, and the cost of rice is Rs. 8 per kg.

NCERT solutions for class 12 maths chapter 4 Determinants: Miscellaneous exercise

Question:1 Prove that the determinant $\begin{vmatrix} x & \sin \theta &\cos \theta \\ -\sin \theta &-x & 1\\ \cos \theta &1 &x \end{vmatrix}$ is independent of $\theta$ .

Answer:

Calculating the determinant value of $\begin{vmatrix} x & \sin \theta &\cos \theta \\ -\sin \theta &-x & 1\\ \cos \theta &1 &x \end{vmatrix}$ ;

$= x\begin{bmatrix} -x &1 \\ 1& x \end{bmatrix}-\sin \Theta\begin{bmatrix} -\sin \Theta &1 \\ \cos \Theta& x \end{bmatrix} + \cos \Theta \begin{bmatrix} -\sin \Theta &-x \\ \cos \Theta& 1 \end{bmatrix}$

$= x(-x^2-1)-\sin \Theta (-x\sin \Theta-\cos \Theta)+\cos\Theta(-\sin \Theta+x\cos\Theta)$

$= -x^3-x+x\sin^2 \Theta+ \sin \Theta\cos \Theta-\cos\Theta\sin \Theta+x\cos^2\Theta$

$= -x^3-x+x(\sin^2 \Theta+\cos^2\Theta)$

$= -x^3-x+x = -x^3$

Clearly, the determinant is independent of $\Theta$ .

Question:2 Without expanding the determinant, prove that
$\begin{vmatrix} a &a^2 &bc \\ b& b^2 &ca \\ c & c^2 &ab \end{vmatrix}= \begin{vmatrix} 1 &a^2 &a^3 \\ 1 &b^2 &b^3 \\ 1 & c^2 &c^3 \end{vmatrix}$

Answer:

We have the

$L.H.S. = \begin{vmatrix} a &a^2 &bc \\ b& b^2 &ca \\ c & c^2 &ab \end{vmatrix}$

Multiplying rows with a, b, and c respectively.

$R_{1} \rightarrow aR_{1}, R_{2} \rightarrow bR_{2},\ and\ R_{3} \rightarrow cR_{3}$

we get;

$= \frac{1}{abc} \begin{vmatrix} a^2 &a^3 &abc \\ b^2& b^3 &abc \\ c^2& c^3 & abc \end{vmatrix}$

$= \frac{1}{abc}.abc \begin{vmatrix} a^2 &a^3 & 1\\ b^2& b^3 &1 \\ c^2& c^3 & 1 \end{vmatrix}$ $[after\ taking\ out\ abc\ from\ column\ 3].$

$= \begin{vmatrix} a^2 &a^3 & 1\\ b^2& b^3 &1 \\ c^2& c^3 & 1 \end{vmatrix} = \begin{vmatrix} 1&a^2 & a^3\\ 1& b^2 &b^3 \\ 1& c^2 & c^3 \end{vmatrix}$ $[Applying\ C_{1}\leftrightarrow C_{3}\ and\ C_{2} \leftrightarrow C_{3}]$

= R.H.S.

Hence proved. L.H.S. =R.H.S.

Question:3 Evaluate $\begin{vmatrix} \cos \alpha \cos \beta & \cos \alpha \sin \beta &-\sin \alpha \\ -\sin \beta & \cos \beta &0 \\ \sin \alpha \cos \beta &\sin \alpha \sin \beta & \cos \alpha \end{vmatrix}$ .

Answer:

Given determinant $\begin{vmatrix} \cos \alpha \cos \beta & \cos \alpha \sin \beta &-\sin \alpha \\ -\sin \beta & \cos \beta &0 \\ \sin \alpha \cos \beta &\sin \alpha \sin \beta & \cos \alpha \end{vmatrix}$ ;

$= \cos \alpha \cos \beta \begin{vmatrix} \cos \beta &0 \\ \sin \alpha \sin \beta & \cos \alpha \end{vmatrix} - \cos \alpha \sin \beta \begin{vmatrix} -\sin \beta & 0 \\ \sin \alpha \cos \beta & \cos \alpha \end{vmatrix} -\sin \alpha \begin{vmatrix} -\sin \beta &\cos \beta \\ \sin \alpha \cos \beta& \sin \alpha \sin \beta \end{vmatrix}$ $= \cos \alpha \cos \beta (\cos \beta \cos \alpha -0 )- \cos \alpha \sin \beta (-\cos \alpha\sin \beta- 0) -\sin \alpha (-\sin \alpha\sin^2\beta - \sin \alpha \cos^2 \beta)$

$= \cos^2 \alpha \cos^2 \beta + \cos^2 \alpha \sin^2 \beta +\sin^2 \alpha \sin^2\beta + \sin^2 \alpha \cos^2 \beta$

$= \cos^2 \alpha(\cos^2 \beta+\sin^2 \beta) +\sin^2 \alpha(\sin^2\beta+\cos^2 \beta)$

$= \cos^2 \alpha(1) +\sin^2 \alpha(1) = 1$ .

Question:4 If $a,b$ and $c$ are real numbers, and

$\Delta =\begin{vmatrix} b+c & c+a &a+b \\ c+a &a+b &b+c \\ a+b & b+c & c+a \end{vmatrix}=0$

Show that either $a+b+c=0$ or $a=b=c$

Answer:

We have given $\Delta =\begin{vmatrix} b+c & c+a &a+b \\ c+a &a+b &b+c \\ a+b & b+c & c+a \end{vmatrix}=0$

Applying the row transformations; $R_{1} \rightarrow R_{1} +R_{2} +R_{3}$ we have;

$\Delta =\begin{vmatrix} 2(a+b+c) & 2(a+b+c) &2(a+b+c) \\ c+a &a+b &b+c \\ a+b & b+c & c+a \end{vmatrix}$

Taking out common factor 2(a+b+c) from the first row;

$\Delta =2(a+b+c)\begin{vmatrix} 1 & 1 &1 \\ c+a &a+b &b+c \\ a+b & b+c & c+a \end{vmatrix}$

Now, applying the column transformations; $C_{1}\rightarrow C_{1} - C_{2}\ and\ C_{2} \rightarrow C_{2}- C_{3}$

we have;

$=2(a+b+c)\begin{vmatrix} 0 & 0 &1 \\ c-b &a-c &b+c \\ a-c & b-a & c+a \end{vmatrix}$

$=2(a+b+c)[(c-b)(b-a)-(a-c)^2]$

$=2(a+b+c)[ab+bc+ca-a^2-b^2-c^2]$

and given that the determinant is equal to zero. i.e., $\triangle = 0$ ;

$(a+b+c)[ab+bc+ca-a^2-b^2-c^2] = 0$

So, either $(a+b+c) = 0$ or $[ab+bc+ca-a^2-b^2-c^2] = 0$ .

we can write $[ab+bc+ca-a^2-b^2-c^2] = 0$ as;

$\Rightarrow -2ab-2bc-2ca+2a^2+2b^2+2c^2 =0$

$\Rightarrow (a-b)^2+(b-c)^2+(c-a)^2 =0$

$\because (a-b)^2,(b-c)^2,\ and\ (c-a)^2$ are non-negative.

Hence $(a-b)^2= (b-c)^2=(c-a)^2 = 0$ .

we get then $a=b=c$

Therefore, if given $\triangle$ = 0 then either $(a+b+c) = 0$ or $a=b=c$ .

Question:5 Solve the equation

$\begin{vmatrix} x+a & x &x \\ x &x+a &x\\ x & x & x+a \end{vmatrix}=0; a\neq 0$

Answer:

Given determinant $\begin{vmatrix} x+a & x &x \\ x &x+a &x\\ x & x & x+a \end{vmatrix}=0; a\neq 0$

Applying the row transformation; $R_{1} \rightarrow R_{1}+R_{2}+R_{3}$ we have;

$\begin{vmatrix} 3x+a & 3x+a &3x+a \\ x &x+a &x\\ x & x & x+a \end{vmatrix} =0$

Taking common factor (3x+a) out from first row.

$(3x+a)\begin{vmatrix} 1 & 1 &1 \\ x &x+a &x\\ x & x & x+a \end{vmatrix} =0$

Now applying the column transformations; $C_{1} \rightarrow C_{1}-C_{2}$ and $C_{2} \rightarrow C_{2}-C_{3}$ .

we get;

$(3x+a)\begin{vmatrix} 0 & 0 &1 \\ -a &a &x\\ 0 & -a & x+a \end{vmatrix} =0$

$=(3x+a)(a^2)=0$ as $a^2 \neq 0$ ,

or $3x+a=0$ or $x= -\frac{a}{3}$

Question:6 Prove that $\begin{vmatrix} a^2 &bc &ac+a^2 \\ a^2+ab & b^2 & ac\\ ab &b^2+bc &c^2 \end{vmatrix}=4a^2b^2c^2$ .

Answer:

Given matrix $\begin{vmatrix} a^2 &bc &ac+a^2 \\ a^2+ab & b^2 & ac\\ ab &b^2+bc &c^2 \end{vmatrix}$

Taking common factors a,b and c from the column $C_{1}, C_{2}, and\ C_{3}$ respectively.

we have;

$\triangle = abc\begin{vmatrix} a &c &a+c \\ a+b & b & a\\ b &b+c &c \end{vmatrix}$

Applying $R_{2} \rightarrow R_{2}-R_{1}\ and\ R_{3} \rightarrow R_{3} - R_{1}$ , we have;

$\triangle = abc\begin{vmatrix} a &c &a+c \\ b & b-c &-c\\ b-a &b &-a \end{vmatrix}$

Then applying $R_{2} \rightarrow R_{2}+R_{1}$ , we get;

$\triangle = abc\begin{vmatrix} a &c &a+c \\ a+b & b &a\\ b-a &b &-a \end{vmatrix}$

Applying $R_{3} \rightarrow R_{3}+R_{2}$ , we have;

$\triangle = abc\begin{vmatrix} a &c &a+c \\ a+b & b &a\\ 2b &2b &0 \end{vmatrix} = 2ab^2c\begin{vmatrix} a &c &a+c \\ a+b & b &a\\ 1 &1 &0 \end{vmatrix}$

Now, applying column transformation; $C_{2} \rightarrow C_{2 }-C_{1}$ , we have

$\triangle = 2ab^2c\begin{vmatrix} a &c-a &a+c \\ a+b & -a &a\\ 1 &0 &0 \end{vmatrix}$

So we can now expand the remaining determinant along $R_{3}$ we have;

$\triangle = 2ab^2c\left [ a(c-a)+a(a+c) \right ]$

$= 2ab^2c\left [ ac-a^2+a^2+ac) \right ] = 2ab^2c\left [ 2ac \right ]$

$= 4a^2b^2c^2$

Hence proved.

Question:7 If $A^-^1=\begin{bmatrix} 3 &-1 &1 \\ -15 &6 &-5 \\ 5 &-2 &2 \end{bmatrix}$ and $B=\begin{bmatrix} 1 &2 &-2 \\ -1&3 &0 \\ 0 &-2 &1 \end{bmatrix}$ , find $(AB)^-^1$ .

Answer:

We know from the identity that;

$(AB)^{-1} = B^{-1}A^{-1}$ .

Then we can find easily,

Given $A^-^1=\begin{bmatrix} 3 &-1 &1 \\ -15 &6 &-5 \\ 5 &-2 &2 \end{bmatrix}$ and $B=\begin{bmatrix} 1 &2 &-2 \\ -1&3 &0 \\ 0 &-2 &1 \end{bmatrix}$

Then we have to basically find the $B^{-1}$ matrix.

So, Given matrix $B=\begin{bmatrix} 1 &2 &-2 \\ -1&3 &0 \\ 0 &-2 &1 \end{bmatrix}$

$|B| = 1(3-0) -2(-1-0)-2(2-0) = 3+2-4 = 1 \neq 0$

Hence its inverse $B^{-1}$ exists;

Now, as we know that

$B^{-1} = \frac{1}{|B|} adjB$

So, calculating cofactors of B,

$B_{11} = (-1)^{1+1}(3-0) = 3$ $B_{12} = (-1)^{1+2}(-1-0) = 1$

$B_{13} = (-1)^{1+3}(2-0) = 2$ $B_{21} = (-1)^{2+1}(2-4) = 2$

$B_{22} = (-1)^{2+2}(1-0) = 1$ $B_{23} = (-1)^{2+3}(-2-0) = 2$

$B_{31} = (-1)^{3+1}(0+6) = 6$ $B_{32} = (-1)^{3+2}(0-2) = 2$

$B_{33} = (-1)^{3+3}(3+2) = 5$

$adjB = \begin{bmatrix} 3 &2 &6 \\ 1& 1& 2\\ 2& 2& 5 \end{bmatrix}$

$B^{-1} = \frac{1}{|B|} adjB = \frac{1}{1} \begin{bmatrix} 3 &2 &6 \\ 1& 1& 2\\ 2& 2& 5 \end{bmatrix}$

Now, We have both $A^{-1}$ as well as $B^{-1}$ ;

Putting in the relation we know; $(AB)^{-1} = B^{-1}A^{-1}$

$(AB)^{-1}=\frac{1}{1} \begin{bmatrix} 3 &2 &6 \\ 1& 1& 2\\ 2& 2& 5 \end{bmatrix}\begin{bmatrix} 3 &-1 &1 \\ -15 &6 &-5 \\ 5 &-2 &2 \end{bmatrix}$

$= \begin{bmatrix} 9-30+30 &-3+12-12 &3-10+12 \\ 3-15+10&-1+6-4 &1-5+4 \\ 6-30+25 &-2+12-10 &2-10+10 \end{bmatrix}$

$= \begin{bmatrix} 9 &-3 &5 \\ -2&1 &0 \\ 1 &0 &2\end{bmatrix}$

Question:8(i) Let $A=\begin{bmatrix} 1 &2 &1 \\ 2 &3 &1 \\ 1 & 1 & 5 \end{bmatrix}$ . Verify that,

$\dpi{100} [adj A]^-^1 = adj (A^-^1)$

Answer:

Given that $A=\begin{bmatrix} 1 &2 &1 \\ 2 &3 &1 \\ 1 & 1 & 5 \end{bmatrix}$ ;

So, let us assume that $A^{-1} = B$ matrix and $adjA = C$ then;

$|A| = 1(15-1) -2(10-1) +1(2-3) = 14-18-1 = -5 \neq 0$

Hence its inverse exists;

$A^{-1} = \frac{1}{|A|} adjA$ or $B = \frac{1}{|A|}C$ ;

so, we now calculate the value of $adjA$

Cofactors of A;

$A_{11}= (-1)^{1+1}(15-1) = 14$ $A_{12}= (-1)^{1+2}(10-1) = -9$

$A_{13}= (-1)^{1+3}(2-3) = -1$ $A_{21}= (-1)^{2+1}(10-1) = -9$

$A_{22}= (-1)^{2+2}(5-1) = 4$ $A_{23}= (-1)^{2+3}(1-2) = 1$

$A_{31}= (-1)^{3+1}(2-3) = -1$ $A_{32}= (-1)^{3+2}(1-2) = 1$

$A_{33}= (-1)^{3+3}(3-4) = -1$

$\Rightarrow adjA =C= \begin{bmatrix} 14 &-9 &-1 \\ -9& 4& 1\\ -1& 1 &-1 \end{bmatrix}$

$A^{-1} =B= \frac{1}{|A|} adjA = \frac{1}{-5}\begin{bmatrix} 14 &-9 &-1 \\ -9& 4& 1\\ -1& 1 &-1 \end{bmatrix}$

Finding the inverse of C;

$|C| = 14(-4-1)+9(9+1)-1(-9+4) = -70+90+5 = 25 \neq 0$

Hence its inverse exists;

$C^{-1} = \frac{1}{|C|}adj C$

Now, finding the $adjC$ ;

$C_{11}= (-1)^{1+1}(-4-1) = -5$ $C_{12}= (-1)^{1+2}(9+1) = -10$

$C_{13}= (-1)^{1+3}(-9+4) = -5$ $C_{21}= (-1)^{2+1}(9+1) = -10$

$C_{22}= (-1)^{2+2}(-14-1) = -15$ $C_{23}= (-1)^{2+3}(14-9) = -5$

$C_{31}= (-1)^{3+1}(-9+4) = -5$ $C_{32}= (-1)^{3+2}(14-9) = -5$

$C_{33}= (-1)^{3+3}(56-81) = -25$

$adjC = \begin{bmatrix} -5 &-10 &-5 \\ -10& -15 & -5\\ -5& -5& -25 \end{bmatrix}$

$C^{-1} = \frac{1}{|C|}adjC = \frac{1}{25}\begin{bmatrix} -5 &-10 &-5 \\ -10& -15 & -5\\ -5& -5& -25 \end{bmatrix} = \begin{bmatrix} -\frac{1}{5} && -\frac{2}{5} &&-\frac{1}{5} \\ \\ -\frac{2}{5}&& -\frac{3}{5} && -\frac{1}{5}\\ \\ -\frac{1}{5} && -\frac{1}{5} && -1 \end{bmatrix}$

or $L.H.S. = C^{-1} = [adjA]^{-1} = \begin{bmatrix} -\frac{1}{5} && -\frac{2}{5} &&-\frac{1}{5} \\ \\ -\frac{2}{5}&& -\frac{3}{5} && -\frac{1}{5}\\ \\ -\frac{1}{5} && -\frac{1}{5} && -1 \end{bmatrix}$

Now, finding the R.H.S.

$adj (A^{-1}) = adj B$

$A^{-1} =B= \begin{bmatrix} \frac{-14}{5} &&\frac{9}{5} &&\frac{1}{5} \\ \\ \frac{9}{5}&& \frac{-4}{5}&& \frac{-1}{5}\\ \\ \frac{1}{5}&& \frac{-1}{5} &&\frac{1}{5}\end{bmatrix}$

Cofactors of B;

$B_{11}= (-1)^{1+1}(\frac{-4}{25}-\frac{1}{25}) = \frac{-1}{5}$

$B_{12}= (-1)^{1+2}(\frac{9}{25}+\frac{1}{25}) =- \frac{2}{5}$

$B_{13}= (-1)^{1+3}(\frac{-9}{25}+\frac{4}{25}) = \frac{-1}{5}$

$B_{21}= (-1)^{2+1}(\frac{9}{25}+\frac{1}{25}) = -\frac{2}{5}$

$B_{22}= (-1)^{2+2}(\frac{-14}{25}-\frac{1}{25}) = \frac{-3}{5}$

$B_{23}= (-1)^{2+3}(\frac{14}{25}-\frac{9}{25}) = \frac{-1}{5}$

$B_{31}= (-1)^{3+1}(\frac{-9}{25}+\frac{4}{25}) = \frac{-1}{5}$

$B_{32}= (-1)^{3+2}(\frac{14}{25}-\frac{9}{25}) = \frac{-1}{5}$

$B_{33}= (-1)^{3+3}(\frac{56}{25}-\frac{81}{25}) = -1$

$R.H.S. = adjB = adj(A^{-1}) =\begin{bmatrix} -\frac{1}{5} && -\frac{2}{5} &&-\frac{1}{5} \\ \\ -\frac{2}{5}&& -\frac{3}{5} && -\frac{1}{5}\\ \\ -\frac{1}{5} && -\frac{1}{5} && -1 \end{bmatrix}$

Hence L.H.S. = R.H.S. proved.

Question:8(ii) Let $A=\begin{bmatrix} 1 &2 &1 \\ 2 & 3 &1 \\ 1 & 1 & 5 \end{bmatrix}$ , Verify that

$(A^-^1)^-^1=A$

Answer:

Given that $A=\begin{bmatrix} 1 &2 &1 \\ 2 &3 &1 \\ 1 & 1 & 5 \end{bmatrix}$ ;

So, let us assume that $A^{-1} = B$

$|A| = 1(15-1) -2(10-1) +1(2-3) = 14-18-1 = -5 \neq 0$

Hence its inverse exists;

$A^{-1} = \frac{1}{|A|} adjA$ or $B = \frac{1}{|A|}C$ ;

so, we now calculate the value of $adjA$

Cofactors of A;

$A_{11}= (-1)^{1+1}(15-1) = 14$ $A_{12}= (-1)^{1+2}(10-1) = -9$

$A_{13}= (-1)^{1+3}(2-3) = -1$ $A_{21}= (-1)^{2+1}(10-1) = -9$

$A_{22}= (-1)^{2+2}(5-1) = 4$ $A_{23}= (-1)^{2+3}(1-2) = 1$

$A_{31}= (-1)^{3+1}(2-3) = -1$ $A_{32}= (-1)^{3+2}(1-2) = 1$

$A_{33}= (-1)^{3+3}(3-4) = -1$

$\Rightarrow adjA =C= \begin{bmatrix} 14 &-9 &-1 \\ -9& 4& 1\\ -1& 1 &-1 \end{bmatrix}$

$A^{-1} =B= \frac{1}{|A|} adjA = \frac{1}{-5}\begin{bmatrix} 14 &-9 &-1 \\ -9& 4& 1\\ -1& 1 &-1 \end{bmatrix} = \begin{bmatrix} \frac{-14}{5} &&\frac{9}{5} &&\frac{1}{5} \\ \\ \frac{9}{5} && \frac{-4}{5} &&\frac{-1}{5} \\ \\ \frac{1}{5} &&\frac{-1}{5} &&\frac{1}{5} \end{bmatrix}$

Finding the inverse of B ;

$|B| = \frac{-14}{5}(\frac{-4}{25}-\frac{1}{25})-\frac{9}{5}(\frac{9}{25}+\frac{1}{25})+\frac{1}{5}(\frac{-9}{25}+\frac{4}{25})$

$= \frac{70}{125}-\frac{90}{125}-\frac{5}{125} = \frac{-25}{125} = \frac{-1}{5} \neq 0$

Hence its inverse exists;

$B^{-1} = \frac{1}{|B|}adj B$

Now, finding the $adjB$ ;

$B_{11}= (-1)^{1+1}(\frac{-4}{25}-\frac{1}{25}) = \frac{-1}{5}$ $B_{12}= (-1)^{1+2}(\frac{9}{25}+\frac{1}{25}) = \frac{-2}{5}$

$B_{13}= (-1)^{1+3}(\frac{-9}{25}+\frac{4}{25}) = \frac{-1}{5}$ $B_{21}= (-1)^{2+1}(\frac{9}{25}+\frac{1}{25}) = -\frac{2}{5}$

$B_{22}= (-1)^{2+2}(\frac{-14}{25}-\frac{1}{25}) = \frac{-3}{5}$ $B_{23}= (-1)^{2+3}(\frac{14}{25}-\frac{9}{25}) = \frac{-1}{5}$

$B_{31}= (-1)^{3+1}(\frac{-9}{25}+\frac{4}{25}) = \frac{-1}{5}$

$B_{32}= (-1)^{3+2}(\frac{14}{25}-\frac{9}{25}) = \frac{-1}{5}$

$B_{33}= (-1)^{3+3}(\frac{56}{25}-\frac{81}{25}) = \frac{-25}{25} =-1$

$adjB = \begin{bmatrix} \frac{-1}{5} &&\frac{-2}{5} &&\frac{-1}{5} \\ \\\frac{-2}{5}&& \frac{-3}{5} && \frac{-1}{5}\\ \\ \frac{-1}{5}&& \frac{-1}{5}&& -1 \end{bmatrix}$

$B^{-1} = \frac{1}{|B|}adjB = \frac{-5}{1}\begin{bmatrix} \frac{-1}{5} &&\frac{-2}{5} &&\frac{-1}{5} \\ \\\frac{-2}{5}&& \frac{-3}{5} && \frac{-1}{5}\\ \\ \frac{-1}{5}&& \frac{-1}{5}&& -1 \end{bmatrix}= \begin{bmatrix} 1 &2 &1 \\ 2& 3& 1\\ 1 & 1 &5 \end{bmatrix}$

$L.H.S. = B^{-1} = (A^{-1})^{-1} = \begin{bmatrix} 1 &2 &1 \\ 2& 3& 1\\ 1 & 1 &5 \end{bmatrix}$

$R.H.S. = A = \begin{bmatrix} 1 &2 &1 \\ 2& 3& 1\\ 1& 1 &5 \end{bmatrix}$

Hence proved L.H.S. =R.H.S. .

Question:9 Evaluate $\begin{vmatrix} x & y &x+y \\ y & x+y &x \\ x+y & x & y \end{vmatrix}$

Answer:

We have determinant $\triangle = \begin{vmatrix} x & y &x+y \\ y & x+y &x \\ x+y & x & y \end{vmatrix}$

Applying row transformations; $R_{1} \rightarrow R_{1}+R_{2}+R_{3}$ , we have then;

$\triangle = \begin{vmatrix} 2(x+y) & 2(x+y) &2(x+y) \\ y & x+y &x \\ x+y & x & y \end{vmatrix}$

Taking out the common factor 2(x+y) from the row first.

$= 2(x+y)\begin{vmatrix} 1 & 1 &1 \\ y & x+y &x \\ x+y & x & y \end{vmatrix}$

Now, applying the column transformation; $C_{1} \rightarrow C_{1} - C_{2}$ and $C_{2} \rightarrow C_{2} - C_{1}$ we have ;

$= 2(x+y)\begin{vmatrix} 0 & 0 &1 \\ -x & y &x \\ y & x-y & y \end{vmatrix}$

Expanding the remaining determinant;

$= 2(x+y)(-x(x-y)-y^2) = 2(x+y)[-x^2+xy-y^2]$

$= -2(x+y)[x^2-xy+y^2] = -2(x^3+y^3)$ .

Question:10 Evaluate $\begin{vmatrix} 1 & x &y \\ 1 &x+y &y \\ 1 &x &x+y \end{vmatrix}$

Answer:

We have determinant $\triangle = \begin{vmatrix} 1 & x &y \\ 1 &x+y &y \\ 1 &x &x+y \end{vmatrix}$

Applying row transformations; $R_{1} \rightarrow R_{1}-R_{2}$ and $R_{2} \rightarrow R_{2}-R_{3}$ then we have then;

$\triangle = \begin{vmatrix} 0 & -y &0 \\ 0 &y &-x \\ 1 &x &x+y \end{vmatrix}$

Taking out the common factor -y from the row first.

$\triangle = -y\begin{vmatrix} 0 & 1 &0 \\ 0 &y &-x \\ 1 &x &x+y \end{vmatrix}$

Expanding the remaining determinant;

$-y[1(-x-o)] = xy$

Question:11 Using properties of determinants, prove that

$\begin{vmatrix} \alpha & \alpha ^2 &\beta +\gamma \\ \beta & \beta ^2 &\gamma +\alpha \\ \gamma &\gamma ^2 &\alpha +\beta \end{vmatrix}=(\beta -\gamma )(\gamma -\alpha )(\alpha -\beta )(\alpha +\beta +\gamma )$

Answer:

Given determinant $\triangle = \begin{vmatrix} \alpha & \alpha ^2 &\beta +\gamma \\ \beta & \beta ^2 &\gamma +\alpha \\ \gamma &\gamma ^2 &\alpha +\beta \end{vmatrix}$

Applying Row transformations; and $R_{3} \rightarrow R_{3}-R_{1}$ , then we have;

$\triangle = \begin{vmatrix} \alpha & \alpha ^2 &\beta +\gamma \\ \beta -\alpha & \beta ^2 - \alpha^2 &\alpha - \beta \\ \gamma-\alpha &\gamma ^2-\alpha^2 &\alpha -\gamma \end{vmatrix}$

$= (\beta-\alpha)(\gamma-\alpha)\begin{vmatrix} \alpha & \alpha ^2 &\beta +\gamma \\ 1 & \beta + \alpha &-1 \\ 0 &\gamma-\beta &0\end{vmatrix}$

Expanding the remaining determinant;

$= (\beta-\alpha)(\gamma-\alpha)[-(\gamma-\beta)(-\alpha-\beta-\gamma)]$

$= (\beta-\alpha)(\gamma-\alpha)(\gamma-\beta)(\alpha+\beta+\gamma)$

$=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)(\alpha+\beta+\gamma)$

hence the given result is proved.

Question:12 Using properties of determinants, prove that

$\begin{vmatrix} x & x^2&1+px^3 \\ y& y^2& 1+py^3\\ z&z^2 & 1+pz^3 \end{vmatrix}=(1+pxyz)(x-y)(y-z)(z-x),$ where p is any scalar.

Answer:

Given the determinant $\triangle = \begin{vmatrix} x & x^2&1+px^3 \\ y& y^2& 1+py^3\\ z&z^2 & 1+pz^3 \end{vmatrix}$

Applying the row transformations; $R_{2} \rightarrow R_{2} - R_{1}$ and $R_{3} \rightarrow R_{3} - R_{1}$ then we have;

$\triangle = \begin{vmatrix} x & x^2&1+px^3 \\ y-x& y^2-x^2& p(y^3-x^3)\\ z-x&z^2-x^2 & p(z^3-x^3) \end{vmatrix}$

Applying row transformation $R_{3} \rightarrow R_{3} - R_{2}$ we have then;

$\triangle =(y-x )(z-x)(z-y)\begin{vmatrix} x & x^2&1+px^3 \\ 1& y+x& p(y^2+x^2+xy)\\ 0&1 & p(x+y+z) \end{vmatrix}$

Now we can expand the remaining determinant to get the result;

$\triangle =(y-x )(z-x)(z-y)[(-1)(p)(xy^2+x^3+x^2y)+1+px^3+p(x+y+z)(xy)]$

$=(x-y)(y-z)(z-x)[-pxy^2-px^3-px^2y+1+px^3+px^2y+pxy^2+pxyz]$

$=(x-y)(y-z)(z-x)(1+pxyz)$

hence the given result is proved.

Question:13 Using properties of determinants, prove that

$\begin{vmatrix} 3a &-a+b &-a+c \\ -b+c &3b &-b+c \\ -c+a &-c+b &3c \end{vmatrix}=3(a+b+c)(ab+bc+ca)$

Answer:

Given determinant $\triangle = \begin{vmatrix} 3a &-a+b &-a+c \\ -b+c &3b &-b+c \\ -c+a &-c+b &3c \end{vmatrix}$

Applying the column transformation, $C_{1} \rightarrow C_{1} +C_{2}+C_{3}$ we have then;

$\triangle = \begin{vmatrix} a+b+c &-a+b &-a+c \\ a+b+c &3b &-b+c \\ a+b+c &-c+b &3c \end{vmatrix}$

Taking common factor (a+b+c) out from the column first;

$=(a+b+c) \begin{vmatrix} 1 &-a+b &-a+c \\ 1 &3b &-b+c \\1 &-c+b &3c \end{vmatrix}$

Applying $R_{2} \rightarrow R_{2}-R_{1}$ and $R_{3} \rightarrow R_{3}-R_{1}$ , we have then;

$\triangle=(a+b+c) \begin{vmatrix} 1 &-a+b &-a+c \\ 0 &2b+a &a-b \\0 &a-c &2c+a \end{vmatrix}$

Now we can expand the remaining determinant along $C_{1}$ we have;

$\triangle=(a+b+c) [(2b+a)(2c+a)-(a-b)(a-c)]$

$=(a+b+c) [4bc+2ab+2ac+a^2-a^2+ac+ba-bc]$

$=(a+b+c)(3ab+3bc+3ac)$

$=3(a+b+c)(ab+bc+ac)$

Hence proved.

Question:14 Using properties of determinants, prove that

$\begin{vmatrix} 1 &1+p &1+p+q \\ 2&3+2p &4+3p+2q \\ 3&6+3p & 10+6p+3q \end{vmatrix}=1$

Answer:

Given determinant $\triangle = \begin{vmatrix} 1 &1+p &1+p+q \\ 2&3+2p &4+3p+2q \\ 3&6+3p & 10+6p+3q \end{vmatrix}$

Applying the row transformation; $R_{2} \rightarrow R_{2}-2R_{1}$ and $R_{3} \rightarrow R_{3}-3R_{1}$ we have then;

$\triangle = \begin{vmatrix} 1 &1+p &1+p+q \\ 0&1 &2+p \\ 0&3 & 7+3p \end{vmatrix}$

Now, applying another row transformation $R_{3}\rightarrow R_{3}-3R_{2}$ we have;

$\triangle = \begin{vmatrix} 1 &1+p &1+p+q \\ 0&1 &2+p \\ 0&0 & 1 \end{vmatrix}$

We can expand the remaining determinant along $C_{1}$ , we have;

$\triangle = 1\begin{vmatrix} 1 & 2+p\\ 0 &1 \end{vmatrix} = 1(1-0) =1$

Hence the result is proved.

Question:15 Using properties of determinants, prove that

$\begin{vmatrix} \sin \alpha &\cos \alpha &\cos (\alpha +\delta ) \\ \sin \beta & \cos \beta & \cos (\beta +\delta )\\ \sin \gamma &\cos \gamma & \cos (\gamma +\delta ) \end{vmatrix}=0$

Answer:

Given determinant $\triangle = \begin{vmatrix} \sin \alpha &\cos \alpha &\cos (\alpha +\delta ) \\ \sin \beta & \cos \beta & \cos (\beta +\delta )\\ \sin \gamma &\cos \gamma & \cos (\gamma +\delta ) \end{vmatrix}$

Multiplying the first column by $\sin \delta$ and the second column by $\cos \delta$ , and expanding the third column, we get

$\triangle =\frac{1}{\sin \delta \cos \delta} \begin{vmatrix} \sin \alpha \sin \delta &\cos \alpha\cos \delta &\cos \alpha \cos \delta -\sin \alpha \sin \delta \\ \sin \beta\sin \delta & \cos \beta\cos \delta & \cos \beta \cos \delta - \sin \beta\sin \delta \\ \sin \gamma\sin \delta &\cos \gamma\cos \delta & \cos \gamma \cos\delta- \sin \gamma\sin \delta \end{vmatrix}$

Applying column transformation, $C_{1} \rightarrow C_{1}+C_{3}$ we have then;

$\triangle =\frac{1}{\sin \delta \cos \delta} \begin{vmatrix} \cos \alpha \cos \delta &\cos \alpha\cos \delta &\cos \alpha \cos \delta -\sin \alpha \sin \delta \\ \cos \beta\cos \delta & \cos \beta\cos \delta & \cos \beta \cos \delta - \sin \beta\sin \delta \\ \cos \gamma\cos \delta &\cos \gamma\cos \delta & \cos \gamma \cos\delta- \sin \gamma\sin \delta \end{vmatrix}$

Here we can see that two columns $C_{1}\ and\ C_{2}$ are identical.

The determinant value is equal to zero. $\therefore \triangle = 0$

Hence proved.

Question:16 Solve the system of equations

$\frac{2}{x}+\frac{3}{y}+\frac{10}{z}=4$

$\frac{4}{x}-\frac{6}{y}+\frac{5}{z}=1$

$\frac{6}{x}+\frac{9}{y}-\frac{20}{z}=2$

Answer:

We have a system of equations;

$\frac{2}{x}+\frac{3}{y}+\frac{10}{z}=4$

$\frac{4}{x}-\frac{6}{y}+\frac{5}{z}=1$

$\frac{6}{x}+\frac{9}{y}-\frac{20}{z}=2$

So, we will convert the given system of equations in a simple form to solve the problem by the matrix method;

Let us take, $\frac{1}{x} = a$ , $\frac{1}{y} = b\ and\ \frac{1}{z} = c$

Then we have the equations;

$2a +3b+10c = 4$

$4a-6b+5c =1$

$6a+9b-20c = 2$

We can write it in the matrix form as $AX =B$ , where

$A= \begin{bmatrix} 2 &3 &10 \\ 4& -6 & 5\\ 6 & 9 & -20 \end{bmatrix} , X = \begin{bmatrix} a\\b \\c \end{bmatrix}\ and\ B = \begin{bmatrix} 4\\1 \\ 2 \end{bmatrix}.$

Now, Finding the determinant value of A;

$|A| = 2(120-45)-3(-80-30)+10(36+36)$

$=150+330+720$

$=1200 \neq 0$

Hence we can say that A is non-singular $\therefore$ its invers exists;

Finding cofactors of A;

$A_{11} = 75$ , $A_{12} = 110$ , $A_{13} = 72$

$A_{21} = 150$ , $A_{22} = -100$ , $A_{23} = 0$

$A_{31} =75$ , $A_{31} =30$ , $A_{33} =-24$

$\therefore$ as we know $A^{-1} = \frac{1}{|A|}adjA$

$= \frac{1}{1200} \begin{bmatrix} 75 &150 &75 \\ 110& -100& 30\\ 72&0 &-24 \end{bmatrix}$

Now we will find the solutions by relation $X = A^{-1}B$ .

$\Rightarrow \begin{bmatrix} a\\b \\ c \end{bmatrix} = \frac{1}{1200} \begin{bmatrix} 75 &150 &75 \\ 110& -100& 30\\ 72&0 &-24 \end{bmatrix}\begin{bmatrix} 4\\1 \\ 2 \end{bmatrix}$

$= \frac{1}{1200}\begin{bmatrix} 300+150+150\\440-100+60 \\ 288+0-48 \end{bmatrix}$

$= \frac{1}{1200}\begin{bmatrix} 600\\400\\ 240 \end{bmatrix} = \begin{bmatrix} \frac{1}{2}\\ \\ \frac{1}{3} \\ \\ \frac{1}{5} \end{bmatrix}$

Therefore we have the solutions $a = \frac{1}{2},\ b= \frac{1}{3},\ and\ c = \frac{1}{5}.$

Or in terms of x, y, and z;

$x =2,\ y =3,\ and\ z = 5$

Question:17 Choose the correct answer.

If $a,b,c,$ are in A.P, then the determinant
$\dpi{100} \begin{vmatrix} x+2 &x+3 &x+2a \\ x+3 & x+4 & x+2b\\ x+4 & x+5 &x+2c \end{vmatrix}$ is

(A) $0$ (B) $1$ (C) $x$ (D) $2x$

Answer:

Given determinant $\triangle = \begin{vmatrix} x+2 &x+3 &x+2a \\ x+3 & x+4 & x+2b\\ x+4 & x+5 &x+2c \end{vmatrix}$ and given that a, b, c are in A.P.

That means , 2b =a+c

$\triangle = \begin{vmatrix} x+2 &x+3 &x+2a \\ x+3 & x+4 & x+(a+c)\\ x+4 & x+5 &x+2c \end{vmatrix}$

Applying the row transformations, $R_{1} \rightarrow R_{1} -R_{2}$ and then $R_{3} \rightarrow R_{3} -R_{2}$ we have;

$\triangle = \begin{vmatrix} -1 &-1 &a-c \\ x+3 & x+4 & x+(a+c)\\ 1 & 1 &c-a \end{vmatrix}$

Now, applying another row transformation, $R_{1} \rightarrow R_{1} + R_{3}$ , we have

$\triangle = \begin{vmatrix} 0 &0 &0 \\ x+3 & x+4 & x+(a+c)\\ 1 & 1 &c-a \end{vmatrix}$

Clearly we have the determinant value equal to zero;

Hence the option (A) is correct.

Question:18 Choose the correct answer.

If x, y, z are nonzero real numbers, then the inverse of matrix $A=\begin{bmatrix} x &0 &0 \\ 0 &y &0 \\ 0 & 0 & z \end{bmatrix}$ is

$(A)\begin{bmatrix} x^-^1 &0 &0 \\ 0 &y^-^1 &0 \\ 0 & 0 & z^-^1 \end{bmatrix}$ $(B)xyz\begin{bmatrix} x^-^1 &0 &0 \\ 0 &y^-^1 &0 \\ 0 & 0 & z^-^1 \end{bmatrix}$

$(C)\frac{1}{xyz}\begin{bmatrix} x &0 &0 \\ 0 &y &0 \\ 0 & 0 & z \end{bmatrix}$ $(D)\frac{1}{xyz}\begin{bmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 & 0 & 1 \end{bmatrix}$

Answer:

Given Matrix $A=\begin{bmatrix} x &0 &0 \\ 0 &y &0 \\ 0 & 0 & z \end{bmatrix}$ ,

$|A| = x(yz-0) =xyz$

As we know,

$A^{-1} = \frac{1}{|A|}adjA$

So, we will find the $adjA$ ,

Determining its cofactor first,

$A_{11} = yz$ $A_{12} = 0$ $A_{13} = 0$

$A_{21} = 0$ $A_{22} = xz$ $A_{23} = 0$

$A_{31} = 0$ $A_{32} = 0$ $A_{33} = xy$

Hence $A^{-1} = \frac{1}{|A|}adjA = \frac{1}{xyz}\begin{bmatrix} yz &0 &0 \\ 0& xz & 0\\ 0& 0& xy \end{bmatrix}$

$A^{-1} = \begin{bmatrix} \frac{1}{x} &&0 &&0 \\ 0&& \frac{1}{y} && 0\\ 0&& 0&& \frac{1}{z} \end{bmatrix}$

Therefore the correct answer is (A)

Question:19 Choose the correct answer.

Let $A=\begin{vmatrix} 1 &\sin \theta &1 \\ -\sin \theta & 1 & \sin \theta \\ -1&-\sin \theta &1 \end{vmatrix},$ where $0\leq \theta \leq 2\pi$ . Then

(A) $Det(A)=0$ nbsp; (B) $Det(A)\in (2,\infty)$

Answer:

Given determinant $A=\begin{vmatrix} 1 &\sin \theta &1 \\ -\sin \theta & 1 & \sin \theta \\ -1&-\sin \theta &1 \end{vmatrix}$

$|A| = 1(1+\sin^2 \Theta) -\sin \Theta(-\sin \Theta+\sin \Theta)+1(\sin^2 \Theta +1)$

$= 1+ \sin ^2 \Theta + \sin ^2 \Theta +1$

$= 2+2\sin ^2 \Theta = 2(1+\sin^2 \Theta)$

Now, given the range of $\Theta$ from $0\leq \Theta \leq 2\pi$

$\Rightarrow 0 \leq \sin \Theta \leq 1$

$\Rightarrow 0 \leq \sin^2 \Theta \leq 1$

$\Rightarrow 1 \leq 1+\sin^2 \Theta \leq 2$

$\Rightarrow 2 \leq 2(1+\sin^2 \Theta) \leq 4$

Therefore the $|A|\ \epsilon\ [2,4]$ .

Hence the correct answer is D.

If you are interested in Determinants Class 12 NCERT Solutions exercises then these are listed below.

An insight to the NCERT solutions for Class 12 Maths Chapter 4 Determinants:

The six exercises of NCERT Class 12 Maths solutions chapter 4 Determinants covers the properties of determinants, co-factors and applications like finding the area of triangle, solutions of linear equations in two or three variables, minors, consistency and inconsistency of system of linear equations, adjoint and inverse of a square matrix, and solution of linear equations in two or three variables using inverse of a matrix. You can also check Determinants NCERT solutions if you are facing any problems during practice.

What are the Determinants?

To every square matrix $A=\left [ a_{ij} \right ]$ of order n, we can associate a number (real or complex) called determinant of the square matrix A. Let's take a determinant (A) of order two-

If A is a then the determinant of A is written as |A|

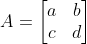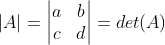
matrix $A=\begin{bmatrix} a &b\\ c & d \end{bmatrix}$ , $|A| =\begin{vmatrix} a & b\\ c& d \end{vmatrix}=det(A)$

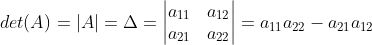
$det(A)=|A| =\Delta =\begin{vmatrix} a_{11} & a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{21}a_{12}$

The six exercises of this chapter determinants covers the properties of determinants, co-factors and applications like finding the area of triangle, solutions of linear equations in two or three variables, minors, consistency and inconsistency of system of linear equations, adjoint and inverse of a square matrix, and solution of linear equations in two or three variables using inverse of a matrix.

Topics and sub-topics of NCERT class 12 maths chapter 4 Determinants

4.1 Introduction

4.2 Determinant

4.2.1 Determinant of a matrix of order one

4.2.2 Determinant of a matrix of order two

4.2.3 Determinant of a matrix of order 3 × 3

4.3 Properties of Determinants

4.4 Area of a Triangle

4.5 Minors and Cofactors

4.6 Adjoint and Inverse of a Matrix

4.7 Applications of Determinants and Matrices

4.7.1 Solution of a system of linear equations using the inverse of a matrix

Also read,

NCERT exemplar solutions class 12 maths chapter 4

Topics of NCERT Class 12 Maths Chapter Determinants

The main topics covered in chapter 4 maths class 12 are:

Determinants

Ch 4 maths class 12 includes concepts of calculation of determinants with respect to their order one, two, three. Also class 12 NCERT topics discuss concepts related to the expansion of the matrix to calculate the determinant. there are good quality questions in Determinants class 12 solutions.

Properties of determinants

This ch 4 maths class 12 comprehensively and elaborately discussed the properties of determinants, which are vastly used. To get a good hold of these concepts you can refer to NCERT solutions for class 12 maths chapter 4.

Area of triangle

This ch 4 maths class 12 also includes concepts of the area of a triangle in which vertices are given. You can refer to class 12 NCERT solutions for questions about these concepts.

Minors and Cofactors

Maths class 12 chapter 4 discussed the minors and cofactors. To get command of these concepts you can go through the NCERT solution for class 12 maths chapter 4.

Adjoint and Inverse of a matrix

concepts related to adjoints and inverse of the matrix are detailed in maths class 12 chapter 4. And it also concerns conditions for the existence of the inverse of a matrix. Determinants class 12 solutions include quality questions to understand the concepts.

Applications of determinants and matrix

ch 4 maths class 12 deliberately discussed the applications of determinants and matrices. it also includes the terms consistent system inconsistent system. concepts related to the solution of a system of linear equations using the inverse of a matrix. For questions on these concepts, you can browse NCERT solutions for class 12 chapter 4.

Topics mentioned in class 12 NCERT are very important and students are suggested to go through all the concepts discussed in the topics. Questions related to all the above topics are covered in the NCERT solutions for class 12 maths chapter 4

NCERT solutions for class 12 Maths - Chapter wise

Chapter 1	NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
Chapter 2	NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
Chapter 3	NCERT solutions for class 12 maths chapter 3 Matrices
Chapter 4	NCERT solutions for class 12 maths chapter 4 Determinants
Chapter 5	NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
Chapter 6	NCERT solutions for class 12 maths chapter 6 Application of Derivatives
Chapter 7	NCERT solutions for class 12 maths chapter 7 Integrals
Chapter 8	NCERT solutions for class 12 maths chapter 8 Application of Integrals
Chapter 9	NCERT solutions for class 12 maths chapter 9 Differential Equations
Chapter 10	NCERT solutions for class 12 maths chapter 10 Vector Algebra
Chapter 11	NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
Chapter 12	NCERT solutions for class 12 maths chapter 12 Linear Programming
Chapter 13	NCERT solutions for class 12 maths chapter 13 Probability

NCERT solutions for class 12 - subject wise

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

NCERT Solutions - Class Wise

SAT® | CollegeBoard

Apply

TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Benefits of NCERT solutions for Class 12 Maths Chapter 4 Determinants:

NCERT Class 12 Maths solutions chapter 4 will assist the students in the exam preparation in a strategic way.
Class 12 Maths Chapter 4 NCERT solutions are prepared by the experts, therefore, students can rely upon the same without any second thought .
NCERT solutions for Class 12 Maths Chapter 4 provides the detailed solution for all the questions. This will help the students in analysing and understanding the questions in a better way.

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

1. What are the key themes discussed in chapter 4 maths class 12 ncert solutions?

NCERT Solutions for Class 12 Maths Chapter 4 primarily focuses on the topic of determinants. This chapter covers the following key themes:

Definition of determinants
Properties of determinants
Area of a parallelogram and a triangle
The inverse of a matrix
Adjoint and inverse of a matrix
Solutions of linear equations using matrices
Determinant as scaling factor

2. What is the weightage of the chapter determinants for CBSE board exam?

The topic algebra which contains two topics matrices and determinants which has 13 % weightage in the maths CBSE 12th board final examination. students can prioritise their subjects according to respective weightage and study accordingly.

3. How are the NCERT solutions helpful in the board exam?

Only knowing the answer does not guarantee to score good marks in the exam. One should know how to answer in order to get good marks. NCERT solutions are provided by the experts who know how best to write answers in the board exam in order to get good marks in the board exam.

4. Which is the best book for CBSE class 12 Maths ?

NCERT textbook is the best book for CBSE class 12 maths. Most of the questions in CBSE class 12 board exam are directly asked from NCERT textbook. So you don't need to buy any supplementary books for CBSE class 12 maths.

5. What applications of determinants are discussed in ncert solutions class 12 maths chapter 4?

According to NCERT Solutions for Class 12 Maths Chapter 4, determinants play a crucial role in algebra and have multiple practical applications. The concept of determinants is valuable in solving systems of linear equations. With determinants, students can explore concepts such as changes in area, volume, and variables through integrals. Additionally, determinants can be used to determine the values of square matrices. Interested students can study determinants class 12 ncert pdf both online and offline.

6. Where can I find the complete solutions of NCERT class 12 Maths ?

Here you will get the detailed NCERT solutions for class 12 maths by clicking on the link. also you can find these in official web page of careers360.

Also Read

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism - Download PDF

NCERT Books for Class 12 Hindi 2024 - Download chapter wise PDFs here

NCERT Books for Class 12 Biology 2024 - Download Free PDF

NCERT Books for Class 12 Chemistry 2024 - Download Free Pdf

NCERT Book for Class 12 Maths 2024 - Download Free PDF

NCERT Book for Class 12 Physics 2024 - Download Free PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Syllabus for Class 12 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 12 2024 (All Subjects) - Download PDF Here

NCERT Syllabus for Class 6 to 12 (2023-24) - All Subjects PDF Download

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions for Class 12 Maths (Updated 2023-24)

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Certifications By Top Providers

Artificial Intelligence Projects

Via Great Learning

Introduction to Web Development with HTML CSS JavaScript

Via IBM

Introduction to Watson AI

Via IBM

Full-Stack Web Development

Via Masai School

Introduction to Data Science

Via IBM

Digital Banking Business Model

Via State Bank of India

1111 courses

788 courses

327 courses

141 courses

Harvard University, Cambridge

98 courses

IBM

85 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

History

Environmental Studies

Psychology

Data Science

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Lancaster University, Lancaster

Bailrigg, Lancaster LA1 4YW

Top Universities in Australia for International Students 2024 - QS Ranking

11 min ⋆ May 02, 2024 12:05 PM IST

SAT Exam Fees 2024 - Registration, Late, Cancellation, Score Services Fee

4 min ⋆ Mar 11, 2024 07:03 AM IST

SAT Sample Papers 2024 - Question Papers PDF for SAT Practice Test

7 min ⋆ May 02, 2024 11:05 AM IST

Top Universities in Canada for International Students 2024 - QS Ranking

9 min ⋆ May 02, 2024 10:05 AM IST

Study MBBS in USA for Indian and International Students 2024

14 min ⋆ Feb 01, 2024 04:02 AM IST

How to Apply for Eligibility Certificate for Studying MBBS Abroad?

6 min ⋆ May 02, 2024 09:05 AM IST

Related E-books & Sample Papers

CBSE Class 11, 12 Physics Syllabus 2024-25

240+ Downloads

CBSE Class 11, 12 Economics Syllabus 2024-25

87+ Downloads

CBSE Class 11, 12 Sociology Syllabus 2024-25

108+ Downloads

CBSE Class 11, 12 Sanskrit (Elective) Syllabus 2024-25

31+ Downloads

CBSE Class 11, 12 Sanskrit (Core) Syllabus 2024-25

9+ Downloads

CBSE Class 11, 12 Psychology Syllabus 2024-25

35+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer

Sajal Trivedi 29 January,2024

i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer

Upasana Barman 24 August,2022

i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.

As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.

Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.

Believe in Yourself! You can make anything happen

All the very best.

Read Complete Answer

Mayankjha.student2007 23 August,2022

if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer

Nuthalapati Vyshnavi 21 August,2022

I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer

Muskan Dhalwal 17 August,2022

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

300M+
Students
36,000+
Colleges
550+
Exams
1500+
E-Books
16000+
Certifications

We Appeared in

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT solutions for Class 12 Maths Chapter 4 Determinants

NCERT Determinants Class 12 Questions And Answers

Applications for Admissions are open.

ALLEN NEET Coaching

Aakash iACST Scholarship Test 2024

NCERT Determinants Class 12 Questions And Answers PDF Free Download

NCERT Class 12 Maths Chapter 4 Question Answer - Important Formulae

NCERT Class 12 Maths Chapter 4 Question Answer (Intext Questions and Exercise)

NCERT determinants class 12 solutions: Excercise: 4.5

An insight to the NCERT solutions for Class 12 Maths Chapter 4 Determinants:

NCERT solutions for class 12 Maths - Chapter wise

NCERT solutions for class 12 - subject wise

NCERT Solutions - Class Wise

SAT® | CollegeBoard

TOEFL ® Registrations 2024

Benefits of NCERT solutions for Class 12 Maths Chapter 4 Determinants:

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)