Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • Show that the line x/a +y/b =1 touches the curve y =b.e^ -x /a at the point where the curve intersects the axis of y.

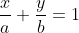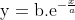Show that the line \frac{x}{a}+\frac{y}{b}=1 touches the curve \mathrm{y}=\mathrm{b.e}^{-\frac{x}{a}} at the point where the curve intersects the axis of y.

Answers (1)

Given: equation of line \frac{x}{a}+\frac{y}{b}=1 the curve \mathrm{y}=\mathrm{b.e}^{-\frac{x}{a}} intersects the y-axis

To show: the line touches the curve at the point where the curve intersects the axis of y

Explanation: given the curve \mathrm{y}=\mathrm{b.e}^{-\frac{x}{a}} intersects the y-axis, i.e., at x = 0

Now differentiate the given curve equation with respect to x, i.e.,

\frac{d y}{d x}=\frac{d\left(b \cdot e^{-\frac{x}{a}}\right)}{d x}$ \\Removing all the constant term, \\$\Rightarrow \frac{d y}{d x}=b \frac{d\left(e^{-\frac{x}{a}}\right)}{d x}$ \\After differentiate in the equation we get \\$\Rightarrow \frac{d y}{d x}=b \cdot e^{-\frac{x}{a}} \frac{d\left(-\frac{x}{a}\right)}{d x}$ \\$\Rightarrow \frac{d y}{d x}=b \cdot e^{-\frac{x}{a}} \cdot\left(-\frac{1}{a}\right)$ \\Now put the value of $x=0$, \\$\Rightarrow\left(\frac{d y}{d x}\right)_{x=0}=b \cdot e^{-\frac{0}{a}} \cdot\left(-\frac{1}{a}\right)$ \\$\Rightarrow\left(\frac{d y}{d x}\right)_{x=0}=$ b. $1 \cdot\left(-\frac{1}{a}\right)$ \\$\Rightarrow\left(\frac{d y}{d x}\right)_{x=0}=\left(-\frac{b}{a}\right)=m_{1} \ldots \ldots(i)

Then considering the line equation,

\frac{x}{a}+\frac{y}{b}=1$ \\Now differentiate it with respect to X \\$\frac{\mathrm{d}\left(\frac{\mathrm{X}}{\mathrm{a}}\right)}{\mathrm{dx}}+\frac{\mathrm{d}\left(\frac{\mathrm{y}}{\mathrm{b}}\right)}{\mathrm{dx}}=\frac{\mathrm{d}(1)}{\mathrm{dx}}$ \\Removing all the constant terms \\$\Rightarrow \frac{1}{a}+\frac{1}{b} \frac{d y}{d x}=0$ \\$\Rightarrow \frac{1}{\mathrm{~b}} \frac{\mathrm{dy}}{\mathrm{dx}}=-\frac{1}{\mathrm{a}}$ \\$\Rightarrow \frac{d y}{d x}=-\frac{b}{a}=m_{2} \ldots .

Line touches the curve only if their slopes are equal

From equation (i) and (ii), we see that

m_1 = m_2

Hence, the line touches the curve at the point where the curve intersects the axis of y.

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question