Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

Edited By Irshad Anwar | Updated on Sep 07, 2023 10:24 PM IST | #CBSE Class 10th

Area Related To Circle Class 10 NCERT Solution

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles are provided here. These NCERT solutions are developed in accordance of latest syllabus and pattern of CBSE 2023-24. NCERT Solutions are important study materials for students in Class 10. These solutions of class 10 area related to circle help students understand the types of questions that will be asked in the CBSE Class 10 Maths board exams and provide solutions to all areas related to circles, which can aid students in preparing effectively for the CBSE exams. NCERT solutions for Class 10 Maths are available at Careers360 and can help students excel in their board exams by providing them with an advance preparation.

This Story also Contains
  1. Area Related To Circle Class 10 NCERT Solution
  2. NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF Free Download
  3. NCERT Solutions for Class 10 Maths Chapter 12 - Important Formulae
  4. NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (Intext Questions and Exercise)
  5. NCERT Solutions of Class 10 - Subject Wise
  6. Key features of Areas Related To Circles Class 10 NCERT solutions
  7. NCERT Class 10 Maths Solutions - Chapter Wise
  8. NCERT Exemplar solutions - Subject Wise
  9. NCERT Books and NCERT Syllabus
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

Also Read,

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF Free Download

Download PDF

NCERT Solutions for Class 10 Maths Chapter 12 - Important Formulae

Circumference of a Circle: Circumference = 2πr

Where r = represents the radius of the circle.

Area of a Circle: Area = πr2

Where r signifies the radius of the circle.

Length of an Arc of a Sector - To find the length of an arc within a sector of a circle, given the radius 'r' and the angle in degrees 'θ', the formula is

Arc Length = 2πr(θ/360)

Area of a Sector of a Circle - For calculating the area of a sector within a circle with radius 'r' and angle in degrees 'θ', the formula is

Sector Area = πr2(θ/360)

Area of a Segment of a Circle - The area of a segment of a circle can be found by subtracting the area of the corresponding triangle from the area of the corresponding sector.

Segment Area = Sector Area - Triangle Area

Segment Area = πr2(θ/360) - (1/2)r2sinθ

When considering the distance moved by a wheel in a single revolution, it is equal to the circumference of the wheel.

Number Of Revolutions = Distance Travelled / circumference = d / 2πr

Free download NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (Intext Questions and Exercise)

NCERT Solutions for Maths Chapter 12 Area Related To Circle Class 10 Excercise: 12.1

Q1 The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.

Answer:

Circumference of 1st circle is given :

\\=\ 2\pi r_1\\\\=\ 2\pi \times 19\ =\ 38 \pi\ cm

And the circumference of the 2nd circle is : =\ 2\pi \times 9\ =\ 18 \pi\ cm

Thus the circumference of the new circle is =\ 18\pi\ +\ 38\pi\ =\ 56\pi\ cm

or 2\pi r =\ 56\pi

or r\ =\ 28\ cm

Hence the radius of the new circle is 28 cm.

Q2 The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.

Answer:

We know that the area of the circle is : =\ \pi r^2

Thus area of a 1st circle : =\ \pi r^2_1

or =\ \pi \times 8^2\ =\ 64 \pi\ cm^2

And the area of a 2nd circle is : =\ \pi r^2_2

or =\ \pi \times 6^2\ =\ 36\pi\ cm^2

According to the question area of the new circle is 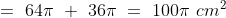=\ 64\pi\ +\ 36\pi\ =\ 100\pi\ cm^2

or \pi r^2\ =\ 100 \pi

or r\ =\ 10\ cm

Hence the area of the new circle is 10 cm.

Q3 Fig. depicts an archery target marked with its five scoring regions from the center outwards as Gold, Red, Blue, Black, and White. The diameter of the region representing the Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

1648791533512

Answer:

The radius of each scoring region can be found by adding 10.5 in respective colors.

The area of the golden region is : =\ \pi r^2\ =\ \pi \times 10.5^2\ =\ 346.5\ cm^2

Similarly area of the red region is = Area of a red score - Area of the golden region

\\=\ \pi \times 21^2\ -\ \pi \times 10.5^2\\\\=\ 1039.5\ cm^2

Then the area of the blue region is :

\\=\ \pi \times (31.5)^2\ -\ \pi \times 21^2\\\\=\ 1732.5\ cm^2

And the area of the black region is :

\\=\ \pi \times 42^2\ -\ \pi \times (31.5)^2\\\\=\ 2425.5\ cm^2

Area of the white region is :

\\=\ \pi \times 52.5^2\ -\ \pi\times 42^2\\\\=\ 3118.5\ cm^2

Q4 The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?

Answer:

Let the number of revolution of the wheel be n.

The circumference of the wheel is given by:-

\\=\ 2\pi r\\\\=\ 2\pi \times 40\ =\ 80\pi\ cm

Now, the speed of the car is given by:-

\\=\ 66\ Km/hr\ \\\\=\ 66\times \frac{100000}{60}\ cm/min\ \\\\=\ 110000\ cm/min.

Thus distance traveled in 10 minutes is: =\ 1100000\ cm

According to the question, we get;

n\times 80\pi\ =\ 1100000

or n\ =\ 4375

Hence the number of revolutions made by the wheel is 4372.

Q5 Tick the correct answer in the following and justify your choice : If the perimeter and the area of a circle are numerically equal, then the radius of the circle is

(A) 2 units
(B) \pi units
(C) 4 units
(D) 7 units

Answer:

Let the radius of the circle be r.

Then according to question, we can write:-

Perimeter = Area

\\2\pi r\ =\ \pi r^2\\\\r\ =\ 2\ units

Hence option (A) is correct.


NCERT Solutions for Maths Chapter 12 Area Related To Circle Class 10 Excercise: 12.2

Q1 Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.

Answer:

We know that the area of a sector having radius r and angle \Theta is given by:-

Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2

Thus the area of the given sector is:-

\\=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 6^2\\\\=\ \frac{132}{7}\ cm^2

Q2 Find the area of a quadrant of a circle whose circumference is 22 cm.

Answer:

We are given the circumference of the circle.

Thus,

\\2\pi r\ =\ 22\\\\r\ =\ \frac{11}{\pi}\ cm

Also, we know that the area of a sector is given by :

Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2

It is given that we need to find the area of a quadrant thus \Theta\ =\ 90^{\circ}

Hence the area becomes:-

\\=\ \frac{90}{360^{\circ}}\times \pi \left ( \frac{11}{\pi} \right )^2\\\\=\ \frac{77}{8}\ cm^2

Q3 The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Answer:

The minute hand rotates 360 o in one hour.

We need to find rotation in 5 min. :-

=\ \frac{360^{\circ}}{60}\times 5\ =\ 30^{\circ}

The area of the sector is given by :

\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{30}{360^{\circ}}\times \pi \times 14^2\\\\Area=\ \frac{154}{3}\ cm^2

Hence the area swept by minute hand in 5 minutes is \frac{154}{3}\ cm^2 .

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (i) minor segment

Answer:

The angle in the minor sector is 90 o .

Thus the area of the sector is given by:-

\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 10^2\\\\Area=\ \frac{1100}{14}\ cm^2\ =\ 78.5\ cm^2

Now the area of a triangle is:-

Area\ =\ \frac{1}{2}bh\ =\ \frac{1}{2}\times 10\times 10\ =\ 50\ cm^2

Thus the area of minor segment = Area of the sector - Area of a triangle

or =\ 78.5\ -\ 50\ =\ 28.5\ cm^2

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (ii) major sector. (Use π = 3.14)

Answer:

The area of the major sector can be found directly by using the formula :

Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2

In the case of this, the angle is 360 o - 90 o = 270 o .

Thus the area is : -

\\=\ \frac{270^{\circ}}{360^{\circ}}\times \pi \times 10\times 10\\\\=\ \frac{3300}{14}\ =\ 235.7\ cm^2

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (i) the length of the arc

Answer:

The length of the arc is given by:-

Length\ of\ arc\ =\ \frac{\Theta}{360^{\circ}} \times 2\pi r

\\=\ \frac{60^{\circ}}{360^{\circ}} \times 2\times \pi \times 21\\\\=\ 22\ cm

Hence the length of the arc is 22 cm.

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (ii) area of the sector formed by the arc

Answer:

We know that the area of the sector is given by:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

\\=\ \frac{60}{360^{\circ}}\ \times \pi \times 21^2\\\\=\ 231\ cm^2

Thus the area of the sector is 231 cm 2 .

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (iii) area of the segment formed by the corresponding chord

Answer:

For the area of the segment, we need to subtract the area of the triangle attached with the area of arc.

Thus consider the triangle:-

It is given that the angle of arc is 60 o , or we can say that all angles are 60 o (since two sides are equal). Hence it is an equilateral triangle.

Area of triangle is:-

\\=\ \frac{\sqrt{3}}{4}\times a^2\\\\\\=\ \frac{\sqrt{3}}{4}\times 21^2\\\\=\ \frac{441\sqrt{3}}{4}\ cm^2

Hence the area of segment is:-

=\ \left (231\ -\ \frac{441\sqrt{3}}{4} \right )\ cm^2

Q6 A chord of a circle of radius 15 cm subtends an angle of 60° at the center. Find the areas of the corresponding minor and major segments of the circle.
(Use \pi = 3.14 and \sqrt 3 = 1.73 )

Answer:

The area of the sector is :

\\=\ \frac{\Theta }{360^{\circ}}\times \pi r^2\\\\=\ \frac{60^{\circ} }{360^{\circ}}\times \pi \times 15^2\\\\=\ 117.85\ cm^2

Now consider the triangle, the angle of the sector is 60 0 .

This implies it is an equilateral triangle. (As two sides are equal so will have the same angle. This possible only when all angles are equal i.e., 60 o .)

Thus, the area of the triangle is:-

=\ \frac{\sqrt{3}}{4}\times 15^2

or =\ 56.25 \sqrt{3}\ =\ 97.31\ cm^2

Hence area of the minor segment : =\117.85\ -\ 97.31\ =\ 20.53\ cm^2

And the area of the major segment is :

=\ \pi r^2\ -\ 20.53

or =\ \pi\times 15^2\ -\ 20.53

or =\ 707.14\ -\ 20.53

or =\ 686.6\ cm^2

Q7 A chord of a circle of radius 12 cm subtends an angle of 120° at the center. Find the area of the corresponding segment of the circle.
(Use \pi = 3.14 and \sqrt3 = 1.73 )

Answer:

For the area of the segment, we need the area of sector and area of the associated triangle.

So, the area of the sector is :

=\ \frac{120^{\circ}}{360^{\circ}}\times \pi \times 12^2

or =\ 150.72\ cm^2

Now, consider the triangle:-

Draw a perpendicular from the center of the circle on the base of the triangle (let it be h).

Using geometry we can write,

\frac{h}{r}\ =\ \cos 60^{\circ}

or h\ =\ 6\ cm

Similarly, \frac{\frac{b}{2}}{r}\ =\ \sin 60^{\circ}

or b\ =\ 12\sqrt{3}\ cm

Thus the area of the triangle is :

=\ \frac{1}{2}\times 12\sqrt{3}\times 6

or =\ 62.28\ cm^2

Hence the area of segment is: =\ 150.72\ -\ 62.28\ =\ 88.44\ cm^2 .

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (i) the area of that part of the field in which the horse can graze.

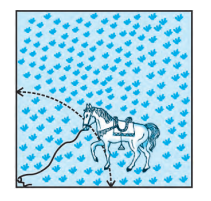
1636091304687

Answer:

The part grazed by the horse is given by = Area of sector

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 5^2

=\ 19.62\ m^2

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use \pi = 3.14 )

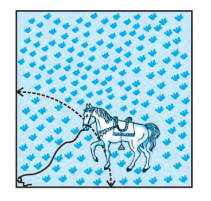
1636091352998

Answer:

When the length of the rope is 10 m, the area grazed will be:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 10^2

=\ 25 \pi\ m^2

Hence the change in the grazing area is given by :

=\ 25 \pi\ -\ \frac{25 \pi}{4}\ =\ 58.85\ m^2

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find: (i) the total length of the silver wire required.

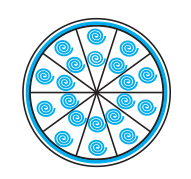
1636091383511

Answer:

The total wire required will be for 5 diameters and the circumference of the brooch.

The circumference of the brooch:-

\\=\ 2\pi r\\\\=\ 2\times \pi \times \frac{35}{2}\\\\=\ 110\ mm

Hence the total wire required will be:- =\ 110\ mm\ +\ 5 \times 35\ mm\ =\ 285\ mm .

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 12.12. Find : (ii) the area of each sector of the brooch.

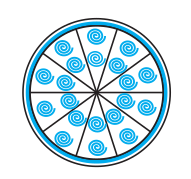
1636091389686

Answer:

The total number of lines present in the brooch is 10 (line starting from the centre).

Thus the angle of each sector is 36 o .

The area of the sector is given by:-

\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{36^{\circ}}{360^{\circ}}\ \times \pi \times \left ( \frac{35}{2} \right )^2\\\\Area=\ \frac{385}{4}\ mm^2

Q10 An umbrella has 8 ribs that are equally spaced (see Fig. ). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

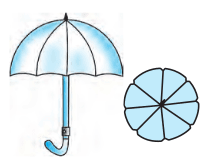
1636091407785

Answer:

It is given that the umbrella has 8 ribs so the angle of each sector is 45 o .

Thus the area of the sector is given by:-

\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{45^{\circ}}{360^{\circ}}\ \times \pi \times 45^2\\\\Area=\ \frac{22275}{28}\ cm^2

Hence the area between two consecutive ribs is \frac{22275}{28}\ cm^2 .

Q11 A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.

Answer:

The area cleaned by one wiper is:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

or =\ \frac{115^{\circ}}{360^{\circ}}\ \times \pi \times 25^2

or =\ \frac{158125}{252}\ cm^2

Hence the required area (area cleaned by both blades) is given by:-

=\ 2\times \frac{158125}{252}\ =\ \frac{158125}{126}\ cm^2

Q12 To warn ships for underwater rocks, a lighthouse spreads a red-colored light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)

Answer:

The area of the sector is given by:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

In this case, the angle is 80 o .

Thus the area is:-

=\ \frac{80^{\circ}}{360^{\circ}}\ \times \pi \times 16.5^2

or =\ 189.97\ Km^2

Q13 A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 0.35 per cm 2 . (Use \sqrt3 = 1.7 )

Answer:

The angle of each of the six sectors is 60 o at the center. \left ( \because \frac{360^{\circ}}{6}\ =\ 60^{\circ} \right )

Area of the sector is given by:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

or =\ \frac{60^{\circ}}{360^{\circ}}\ \times \pi \times 78^2

or =\ 410.66\ cm^2

And the area of the equilateral triangle associated with segment:-

=\ \frac{\sqrt{3}}{4}\times a^2

or =\ \frac{\sqrt{3}}{4}\times 28^2\ =\ 333.2\ cm^2

Hence the area of segment is : =\ 410.66\ -\ 333.2\ =\ 77.46\ cm^2

Thus the total area of design is : =\6\times 77.46\ =\ 464.76\ cm^2

So, the total cost for the design is:- =\ 0.35\times 464.76\ =\ Rs. 162.66

Q14 Tick the correct answer in the following :

Area of a sector of angle p (in degrees) of a circle with radius R is

(A) \frac{p}{180}\times 2\pi R

(B) \frac{p}{180}\times \pi R^2

(C) \frac{p}{360}\times 2\pi R

(D) \frac{p}{720}\times 2\pi R^2

Answer:

We know that the area of the sector is given by:-

Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2

=\ \frac{p}{360^{\circ}}\ \times \pi r^2

Hence option (d) is correct.


NCERT Solutions for Maths Chapter 12 A rea Related To Circle Class 10 Excercise: 12.3

Q1 Find the area of the shaded region in Fig, if PQ = 24 cm, PR = 7 cm, and O is the center of the circle.

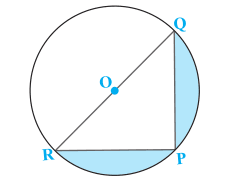
1648791656559

Answer:

We know that \angle RPQ is 90 o as ROQ is the diameter.

RQ can be found using the Pythagoras theorem.

RP^2\ +\ PQ^2\ =\ QR^2

or 7^2\ +\ 24^2\ =\ QR^2

or QR\ =\ \sqrt{625}\ =\ 25\ cm

Now, the area of the shaded region is given by = Area of semicircle - Area of \Delta PQR

Area of a semicircle is:-

=\ \frac{1}{2}\pi r^2

or =\ \frac{1}{2}\pi \times \left ( \frac{25}{2} \right )^2

or =\ 245.53\ cm^2

And, the area of triangle PQR is :

=\ \frac{1}{2}\times 24\times 7\ =\ 84\ cm^2

Hence the area of the shaded region is : =\ 245.53\ -\ 84\ =\ 161.53\ cm^2

Q2 Find the area of the shaded region in Fig, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and \angle AOC = 40\degree .

Answer:

The area of a shaded region can be easily found by using the formula of the area of the sector.

Area of the shaded region is given by : Area of sector OAFC - Area of sector OBED

=\ \frac{40^{\circ}}{360^{\circ}}\times \pi (14)^2\ -\ \frac{40^{\circ}}{360^{\circ}}\times \pi (7)^2

=\ \frac{616}{9}\ -\ \frac{154}{9}\ =\ \frac{462}{9}

=\ 51.33\ cm^2

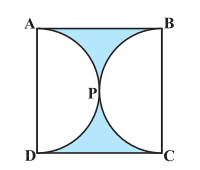
Q3 Find the area of the shaded region in Fig, if ABCD is a square of side 14 cm and APD and BPC are semicircles. 1648791700601

Answer:

Area of the shaded region is given by = Area of the square - Area of two semicircles.

Area of square is : =\ 14^2\ =\ 196\ cm^2

And the area of the semicircle is:-

=\ \frac{1}{2}\pi r^2

=\ \frac{1}{2}\pi \times 7^2

=\ 77\ cm^2

Hence the area of the shaded region is given by : =\ 196 - 2(77) = 42\ cm^2.

Q4 Find the area of the shaded region in Fig, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre. 1648791737051

Answer:

Area of the shaded region is given by = Area of triangle + Area of the circle - Area of the sector

Area of the sector is : -

=\ \frac{60^{\circ}}{360^{\circ}}\times \pi\times 6^2

or =\ \frac{132}{7}\ cm^2

And, the area of the triangle is :

=\ \frac{\sqrt{3}}{4}a^2\ =\ \frac{\sqrt{3}}{4}\times 12^2\ =\ 36\sqrt{3}\ cm^2

And, the area of the circle is : =\ \pi r^2

or =\ \pi \times 6^2

or =\ \frac{792}{7}\ cm^2

Hence the area of the shaded region is:-

=\ 36\sqrt{3}\ +\ \frac{792}{7}\ -\ \frac{132}{7}

or =\ \left ( 36\sqrt{3}\ +\ \frac{660}{7} \right )\ cm^2

Q5 From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. Find the area of the remaining portion of the square. 25793

Answer:

Consider the quadrant in the given figure:- We have an angle of the sector as 90 o and radius 1 cm.

Thus the area of the quadrant is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi\times 1^2

or =\ \frac{22}{28}\ cm^2

And the area of the square is : =\ side^2

=\ 4^2

=\ 16\ cm^2

And, the area of the circle is:-

=\ \pi r^2\ =\ \pi \times 1^2\ =\ \pi\ cm^2

Hence the area of the shaded region is: = Area of the square - Area of the circle - 4 (Area of quadrant)

or =\ 16\ -\ \frac{22}{7}\ -\ 4\left ( \frac{22}{28} \right )

or =\ \frac{68}{7}\ cm^2

Q6 In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. Find the area of the design.

Answer:

Assume the center of the circle to be point C and AD as the median of the equilateral triangle.

Then we can write:-

AO\ =\ \frac{2}{3}AD

or 32\ =\ \frac{2}{3}AD

Thus AD\ =\ 48\ cm

Consider \Delta ABD,

AB^2\ =\ AD^2\ +\ BD^2

or AB^2\ =\ 48^2\ +\ \left ( \frac{AB}{2} \right )^2

or AB\ =\ 32\sqrt{3}\ cm

Thus the area of an equilateral triangle is:-

=\ \frac{\sqrt{3}}{4}\times \left ( 32\sqrt{3} \right )^2

or =\ 768\sqrt{3}\ cm^2

And the area of the circle is : =\ \pi r^2\ =\ \pi\times 32^2

or =\ \frac{22528}{7} cm^2

Hence the area of the design is:-

=\ \left ( \frac{22528}{7}\ -\ 768 \sqrt{3} \right )\ cm^2

Q7. In Fig, ABCD is a square of side 14 cm. With centers A, B, C, and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

Answer:

It is clear from the figure that the area of all sectors is equal (due to symmetry).

Also, the angle of the sector is 90 o and the radius is 7 cm.

Thus the area of the sector is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi (7)^2

or =\ \frac{77}{2}\ cm^2

And, the area of the square is : =\ a^2\ =\ 14^2\ =\ 196\ cm^2

Hence the area of the shaded region is :

=\ 196\ -\ 4\times \frac{77}{2}

=\ 42\ cm^2

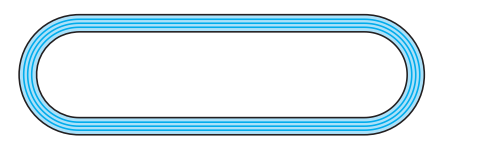
Q8 Fig. depicts a racing track whose left and right ends are semicircular.

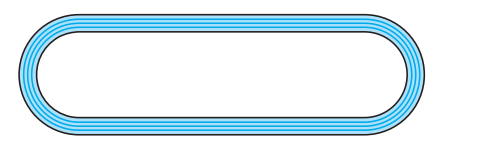
1636091567493

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(i) the distance around the track along its inner edge

Answer:

The distance around the track is Length of two straight lines + Length of two arcs.

Length of the arc is -

=\ \frac{1}{2}\times 2\pi r

=\ \frac{1}{2}\times 2\pi \times 30\ =\ 30\pi\ m

Thus the length of the inner track is :

=\ 106\ +\ 30\pi\ +\ 106\ +\ 30\pi

=\ 212\ +\ 60\pi

=\ \frac{2804}{7}\ m

Q8 Fig. depicts a racing track whose left and right ends are semicircular.

1636091587830

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(ii) the area of the track.

Answer:

The area of track = Area of outer structure - Area of inner structure.

Area of outer structure is: = Area of square + Area of 2 semicircles

=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ m^2

And, area of inner structure: = Area of inner square + Area of 2 inner semicircles

=\ 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2\ m^2

Thus the area of the track is :

\\=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ -\ \left ( 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2 \right )\\\\=\ 4320\ m^2

Hence the area of the track is 4320 m 2 .

Q9 In Fig, AB, and CD are two diameters of a circle (with center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

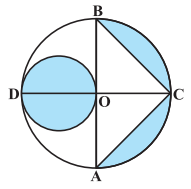
1636091578284

Answer:

Firstly, the area of the smaller circle is :

=\ \pi r^2

=\ \pi \times \left ( \frac{7}{2} \right )^2

=\ \frac{77}{2}\ cm^2

Now, the area of \Delta ABC :-

=\ \frac{1}{2}\times AB\times OC

or =\ \frac{1}{2}\times 14\times 7\ =\ 49\ cm^2

And, the area of the bigger semicircle is :

=\ \frac{1}{2}\pi r^2

=\ \frac{1}{2}\pi \times 7^2

=\ 77\ cm^2

Hence the area of the shaded region is:-

=\ \frac{77}{2}\ +\ 77\ -\ 49

=\ 66.5\ cm^2

Therefore the area of the shaded region is 66.5 cm 2 .

Q10 The area of an equilateral triangle ABC is 17320.5 cm 2 . With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region. (Use \pi = 3.14 and \sqrt3 = 1.73205 )

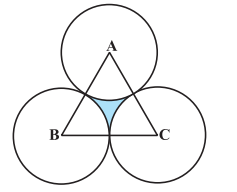
1636091615101

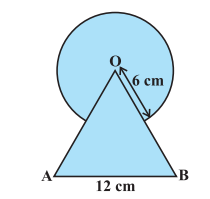
Answer:

Area of an equilateral triangle is:-

=\ \frac{\sqrt{3}}{4}\times a^2

\frac{\sqrt{3}}{4}\times a^2\ =\ 17320.5

a\ =\ 200\ cm

Now, consider the sector:- Angle of the sector is 60 o and the radius is 100 cm.

Thus the area of the sector:-

=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 100^2

=\ \frac{15700}{3}\ cm^2

Thus the area of the shaded region is :

=\ 17320.5\ -\ 3\times \frac{15700}{3}

=\ 1620.5\ cm^2

Q11 On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig.). Find the area of the remaining portion of the handkerchief.

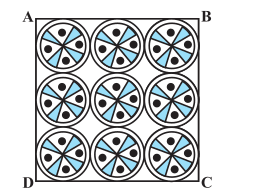
1636091628689

Answer:

Since one side of the square has 3 circles, thus the side of the square is 42 cm.

Area of the square : =\ a^2\ =\ 42^2\ =\ 1764\ cm^2

And, area of a circle :

=\ \pi r^2\ =\ \frac{22}{7}\times 7^2

=\ 154\ cm^2

Hence the area of the remaining portion is : =\ 1764\ -\ 9\times 154

=\ 378\ cm^2

Q12 In Fig, OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB

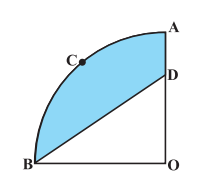
1636091641153

Answer:

The quadrant OACB is a sector with angle 90 o and radius 3.5 cm.

Thus the area of the quadrant is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 3.5^2

=\ \frac{77}{8}\ cm^2

Hence the area of the quadrant is \frac{77}{8}\ cm^2 .

Q12 In Fig, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (ii) shaded region.

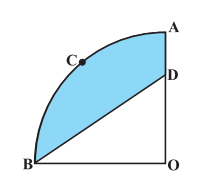
1636091648074

Answer:

For area of shaded region we need to find area of the triangle.

Area of triangle is:-

=\ \frac{1}{2}\times 3.5\times 2

=\ 3.5\ cm^2

Hence the area of the shaded region is = Area of the quadrant - Area of triangle

=\ \frac{77}{8}\ -\ 3.5

=\ \frac{49}{8}\ cm^2

Q13 In Fig, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use \pi = 3.14 )

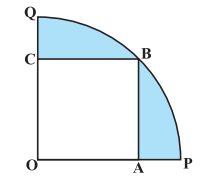
1636091662355

Answer:

In the given figure we need to find the radius of the circle:-

Consider \Delta OAB,

OB^2\ =\ OA^2\ +\ AB^2

=\ 20^2\ +\ 20^2

OB\ =\ 20\sqrt{2}\ cm

Thus area of quadrant:-

=\ \frac{90^{\circ}}{360^{\circ}}\times 3.14\times (20\sqrt{2})^2

=\ 628\ cm^2

Also, the area of the square is : =\ 20^2\ =\ 400\ cm^2

Area of the shaded region is : =\ 628\ -\ 400\ =\ 228\ cm^2

Q14 AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig.). If \angle \textup{AOB} = 30\degree , find the area of the shaded region.

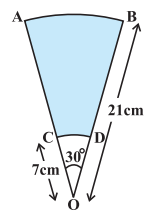
1636091673181

Answer:

Area of the shaded region is = Area of larger sector - Area of smaller sector

=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 21^2\ -\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 7^2

=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times (21^2\ -\ 7^2)

=\ \frac{308}{3}\ cm^2

Hence the area of the shaded region is \frac{308}{3}\ cm^2.

Q15 In Fig, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

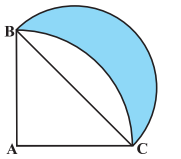
1636091683741

Answer:

Consider \Delta ABC,

BC^2\ =\ AC^2\ +\ AB^2

=\ 14^2\ +\ 14^2

BC\ =\ 14\sqrt{2}\ cm

Area of triangle is :

=\ \frac{1}{2}\times 14\times 14

=\ 98\ cm^2

Now, area of sector is :

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 14^2

=\ 154\ cm^2

And area of semicircle is : -

=\ \frac{1}{2} \pi r^2

=\ \frac{1}{2} \pi \times (7\sqrt{2})^2

=\ 154\ cm^2

Hence the area of the shaded region is : =\ 154\ -\ (154\ -\ 98)\ =\ 98\ cm^2

Q16 Calculate the area of the designed region in fig. common between the two quadrants of circles of radius 8 cm each.

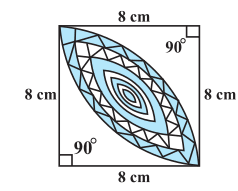
1636091693677

Answer:

It is clear from the figure that the required area (designed area) is the area of the intersection of two sectors.

Area of the sector is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 8^2

=\ \frac{352}{7}\ cm^2

And, area of the triangle:-

=\ \frac{1}{2}\times 8\times 8\ =\ 32\ cm^2

Hence the area of the designed region is :

=\ 2\left ( \frac{352}{7}\ -\ 32 \right )

=\ \frac{256}{7}\ cm^2

NCERT Solutions of Class 10 - Subject Wise

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Key features of Areas Related To Circles Class 10 NCERT solutions

Enhanced Conceptual Understanding: These ch 12 maths class 10 solutions serve as a valuable tool for students seeking to grasp circle-related concepts thoroughly.

Visual Clarity: The ch 12 maths class 10 solutions are thoughtfully supplemented with diagrams, facilitating a more interactive and comprehensive learning journey.

Accessible Language: The language employed in these chapter 12 maths class 10 solutions is intentionally straightforward, ensuring that students can easily grasp the content.

Step-by-Step Guidance: The chapter 12 maths class 10 solutions follow a methodical, step-by-step approach, aiding students in building a strong foundation and understanding the fundamentals with ease.

Individualized Learning: Students have the flexibility to tackle complex problems at their own pace, which fosters self-directed learning and builds problem-solving skills.

Resource Diversity: These ch 12 class 10 maths solutions open doors for students to explore NCERT solutions across various classes and subjects.

Expertly Crafted: These ch 12 class 10 maths solutions are meticulously prepared by experienced educators at Careers360, who prioritize providing clarity on key concepts and nurturing students' problem-solving abilities

Also students can get the solutions for individual exercise-

NCERT Class 10 Maths Solutions - Chapter Wise

Chapter No.

Chapter Name

Chapter 1

Real Numbers

Chapter 2

Polynomials

Chapter 3

Pair of Linear Equations in Two Variables

Chapter 4

Quadratic Equations

Chapter 5

Arithmetic Progressions

Chapter 6

Triangles

Chapter 7

Coordinate Geometry

Chapter 8

Introduction to Trigonometry

Chapter 9

Some Applications of Trigonometry

Chapter 10

Circles

Chapter 11

Constructions

Chapter 12

Areas Related to Circles

Chapter 13

Surface Areas and Volumes

Chapter 14

Statistics

Chapter 15

Probability

NCERT Exemplar solutions - Subject Wise

SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply
Students can also find area related to circle class 10 questions with solutions

NCERT Books and NCERT Syllabus

Tips to Use NCERT Solutions for Class 10 Maths Chapter 12

  • Before starting with this chapter, be well-versed with basic concepts of circles, squares, rectangles, triangles, etc.

  • Learn some formulae related to sectors and segments from the NCERT Class 10 books.

  • Go through some examples given in the textbook and Class 10 Maths Chapter 12 NCERT solutions to understand the approach of solving the problems.

  • After covering the above-said points, it is time to put efforts into practice by practicing the practice exercises.

  • During the practice, one can refer to NCERT solutions for Class 10 Maths chapter 12 to know the correct answer or to know how to solve a particular question.

Happy Learning!

Frequently Asked Question (FAQs)

1. How are the ‘NCERT 10th Class chapter 12 Maths solutions’ helpful in board exam?

As most of the questions in the CBSE board exam are directly asked from the NCERT textbook, so you must know the solutions of questions given in the book. These solutions are provided in a very simple language. To get more problems on the chapter refer to NCERT exemplar problems.

2. How many exercises are there in NCERT Solutions for class 10 areas related to circles?

NCERT solutions for class 10 maths areas related to circles includes 3 exercises with a total of 35 questions. The first exercise covers 5 questions, the second exercise covers 14 questions, and the last exercise covers 16 questions related to the perimeter and area of a circle, areas of a sector and segment of a circle, and areas of combinations of plane figures. Interested students can study area related to circle class 10 pdf online at careers360 website.

3. What are the important concepts from an exam perspective in areas related to circles class 10 solutions?

The key concepts emphasized in area related to circle class 10 solutions that are important from an exam perspective include the introduction to the area of a circle, perimeter and area of a circle, areas of sector and segment of a circle, and areas of combinations of plane figures. Additionally, a summary of the entire chapter class 10 maths areas related to circles is provided

4. What is the significance of studying NCERT Solutions for Class 10 Maths Chapter 12?

The importance of studying class 10 ch area related to circles lies in its ability to provide students with a clear understanding of the question paper pattern and types of questions that may be asked in the board exams, including a mix of repeating, short and long answer, and multiple-choice questions. Practicing a variety of questions can increase students' confidence and increase their chances of success. For ease, students can study areas related to circles class 10 pdf both online and offline mode.

5. Which is the best book for CBSE class 10 maths ?

NCERT textbook is the best book for CBSE class 10 maths. Most of the questions in CBSE class 10 board exam are directly asked from NCERT textbook. All you need to do is rigorous practice of the questions given in the NCER textbook.

6. Which are the most difficult chapter in the NCERT class 10 maths ?

Students consider trigonometry that is introduction to trigonometry and application of trigonometry is most difficult chapter in CBSE class 10 maths. With the regular practice you will get conceptual clarity and will be able to have a strong grip on Trigonometry.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Karnataka Pre-University Certificate Examination

Exam Date:03 May,2024 - 03 May,2024

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:04 May,2024 - 04 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

CBSE Class 9, 10 Odia Syllabus 2024-25

146+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
hindi 10th class mp board sample paper

Dear aspirant !

Hope you are doing well ! The class 10 Hindi mp board sample paper can be found on the given link below . Set your time and give your best in the sample paper it will lead to great results ,many students are already doing so .

https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://school.careers360.com/download/sample-papers/mp-board-10th-hindi-model-paper&ved=2ahUKEwjO3YvJu5KEAxWAR2wGHSLpAiQQFnoECBMQAQ&usg=AOvVaw2qFFjVeuiZZJsx0b35oL1x .

Hope you get it !

Thanking you

Read Complete Answer
Shivanshu 04 February,2024
CBSE class 10th date sheet 11/1/2024 2024

Hello aspirant,

The dates of the CBSE Class 10th and Class 12 exams are February 15–March 13, 2024 and February 15–April 2, 2024, respectively. You may obtain the CBSE exam date sheet 2024 PDF from the official CBSE website, cbse.gov.in.

To get the complete datesheet, you can visit our website by clicking on the link given below.

https://school.careers360.com/boards/cbse/cbse-date-sheet

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 12 January,2024
iam in 7 th plz send 7th previous paper

Hello aspirant,

The paper of class 7th is not issued by respective boards so I can not find it on the board's website. You should definitely try to search for it from the website of your school and can also take advise of your seniors for the same.

You don't need to worry. The class 7th paper will be simple and made by your own school teachers.

Thank you

Hope it helps you.

Read Complete Answer
Sajal Trivedi 25 October,2023
my son's dob is 13/02/2009 is hi eligible for 10th board exam in 2024,,from cbse. olz reply me

The eligibility age criteria for class 10th CBSE is 14 years of age. Since your son will be 15 years of age in 2024, he will be eligible to give the exam.

Read Complete Answer
Shubhangi 29 July,2022
can Hindi marks be replace with IT 402(additional subject) in CBSE class 10th board

That totally depends on what you are aiming for. The replacement of marks of additional subjects and the main subject is not like you will get the marks of IT on your Hindi section. It runs like when you calculate your total percentage you have got, you can replace your lowest marks of the main subjects from the marks of the additional subject since CBSE schools goes for the best five marks for the calculation of final percentage of the students.

However, for the admission procedures in different schools after 10th, it depends on the schools to consider the percentage of main five subjects or the best five subjects to admit the student in their schools.

Read Complete Answer
Aditi Singh 22 July,2022
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
1 days ago :
March 22, 2024 - 08:12 PM IST :
February 02, 2024 - 03:47 PM IST :
CBSE Results 2024: Fake notice goes viral about Class 10th; official dates yet to be announced
May 01, 2024 - 07:45 AM IST
CBSE Class 10, 12 syllabus 2024-25 out; board restores two-level mathematics rule
March 22, 2024 - 08:01 PM IST
CBSE Class 10 board exam 2024 passing criteria, eligibility for compartment; all you need to know
March 20, 2024 - 08:38 PM IST
CBSE directs Class 10, 12 board exam centre superintendents to update OECMS portals
March 13, 2024 - 07:23 PM IST
CBSE Class 10 Computer Applications, IT, AI 2024 Exam Live: Paper analysis, answer key, result date, updates
March 12, 2024 - 03:45 PM IST
CBSE 2024 Maths Exam Live: CBSE Class 10 Mathematics answer key, paper analysis, passing marks, latest updates
March 10, 2024 - 06:18 PM IST
CBSE Class 10 mathematics paper 2024 tomorrow; exam pattern, timings
March 10, 2024 - 07:15 AM IST

Stay up-to date with CBSE Class 10th News

Back to top