Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 12 Maths Chapter 13 Probability

NCERT Solutions for Class 12 Maths Chapter 13 Probability

Edited By Ramraj Saini | Updated on Sep 16, 2023 05:06 PM IST | #CBSE Class 12th

NCERT Probability Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 13 Probability are provided here. You have already studied the basics of probability class 12 in our previous classes like probability as a measure of uncertainty of events in a random experiment, addition rule of probability etc. NCERT solutions for class 12 maths chapter 13 probability will build your base to study probability theory in higher studies therefore probability class 12 ncert solutions become very important.

This Story also Contains
  1. NCERT Probability Class 12 Questions And Answers
  2. NCERT Probability Class 12 Questions And Answers PDF Free Download
  3. NCERT Class 12 Maths Chapter 13 Question Answer Probability - Important Formulae
  4. NCERT Probability Class 12 Questions And Answers (Intext Questions and Exercise)
  5. NCERT class 12 maths chapter 13 Solutions Probability - Topics
  6. NCERT solutions for class 12 maths - Chapter Wise
  7. Key Features of NCERT Solutions for Class 12 Maths Chapter 13 Probability
  8. NCERT solutions for class 12 subject wise
  9. NCERT Solutions class wise
  10. NCERT Books and NCERT Syllabus
  11. NCERT Exemplar Class 12 Solutions

NCERT Class 12 Maths Chapter 13 solutions include concepts of discrete probability, computational probability and stochastic process. The important topics like conditional probability, Bayes' theorem, multiplication rule of probability, and independence of events are covered in this chapter of NCERT Class 12 maths probability books. Questions from all these topics are covered in NCERT solutions for class 12 maths chapter 13 probability.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

Also, you will learn some important concepts of the random variable, probability distribution, and the mean and variance of a probability distribution in this chapter 13 NCERT Class 12 maths solutions PDF. class 12 maths ncert solutions pdf will help you to learn the concept of probability distribution which will be required in higher study. NCERT solutions help students to understan the concepts in a much easy way. Here you will get NCERT solutions for class 12 other subjects also.

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Also read:

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

NCERT Probability Class 12 Questions And Answers PDF Free Download

Download PDF

NCERT Class 12 Maths Chapter 13 Question Answer Probability - Important Formulae

>> Conditional Probability: Conditional probability is the likelihood of an event occurring based on the occurrence of a preceding event. For two events A and B with the same sample space, the conditional probability of event A given that B has occurred (P(A|B)) is defined as:

P(A|B) = P(A ∩ B) / P(B) (when P(B) ≠ 0)

Other conditional probability relationships:

P(S|F) = P(F|F) = 1

P((A ∪ B)|F) = P(A|F) + P(B|F) – P((A ∩ B)|F)

P(E'|F) = 1 − P(E|F)

>> Multiplication Rule: The multiplication rule relates the probability of two events E and F in a sample space S:

P(E ∩ F) = P(E) P(F|E) = P(F) P(E|F) (when P(E) ≠ 0 and P(F) ≠ 0)

>> Independent Events: Two experiments are considered independent if the probability of the events E and F occurring simultaneously is the product of their individual probabilities:

P(E ∩ F) = P(E) * P(F)

>> Bayes’ Theorem: Bayes’ theorem deals with events E1, E2, …, En that form a partition of the sample space S. It allows the calculation of the probability of event Ei given event A:

P(Ei|A) = [P(Ei) * P(A|Ei)] / ∑[P(Ej) * P(A|Ej)], for i = 1, 2, …, n

>> Theorem of Total Probability: Given a partition E1, E2, …, En of the sample space and an event A, the theorem of total probability states:

P(A) = P(E1) * P(A|E1) + P(E2) * P(A|E2) + … + P(En) * P(A|En)

>> Random Variables and their Probability Distributions: A random variable is a real-valued function whose domain is a sample space. The probability distribution of a random variable X consists of possible values x1, x2, …, xn and their corresponding probabilities p1, p2, …, pn:

E(X) = μ = ∑(xi * pi)

Var(X) = σ² = ∑((xi - μ)² * pi)

σ = √Var(X)

Free download NCERT Class 12 Maths Chapter 13 Question Answer Probability for CBSE Exam.

NCERT Probability Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT solutions for class 12 maths chapter 13 probability-Exercise: 13.1


Question:1 Given that E and F are events such that P(E)=0.6,P(F)=0.3 and p(E\cap F)=0.2, find P(E\mid F) and P(F\mid E)

Answer:

It is given that P(E)=0.6,P(F)=0.3 and p(E\cap F)=0.2,

P ( E | F ) = \frac{p(E\cap F)}{P(F)}= \frac{0.2}{0.3}= \frac{2}{3}

P ( F | E ) = \frac{p(E\cap F)}{P(E)}= \frac{0.2}{0.6}= \frac{1}{3}

Question:2 Compute P(A\mid B), if P(B)=0.5 and P(A\cap B)=0.32

Answer:

It is given that P(B)=0.5 and P(A\cap B)=0.32

P ( A | B ) = \frac{p(A\cap B)}{P(B)}= \frac{0.32}{0.5}=0.64

Question:3 If P(A)=0.8,P(B)=0.5 and P(B\mid A)=0.4, find

(i) P(A\cap B)

Answer:

It is given that P(A)=0.8, P(B)=0.5 and P(B|A)=0.4

P ( B | A ) = \frac{p(A\cap B)}{P(A)}

0.4 = \frac{p(A\cap B)} {0.8}

p(A\cap B) = 0.4 \times 0.8

p(A\cap B) = 0.32

Question:3 If P(A)=0.8,P(B)=0.5 and P(B\mid A)=0.4, find

(ii) P(A\mid B)

Answer:

It is given that P(A)=0.8,P(B)=0.5 and P(B\mid A)=0.4,

P(A\cap B)=0.32

P ( A | B ) = \frac{p(A\cap B)}{P(B)}

P ( A | B ) = \frac{0.32}{0.5}

P ( A | B ) = \frac{32}{50}=0.64

Question:3 If P(A)=0.8,P(B)=0.5 and P(B\mid A)=0.4, find

(iii) P(A\cup B)

Answer:

It is given that P(A)=0.8,P(B)=0.5

P(A\cap B)=0.32

P(A\cup B)=P(A)+P(B)-P(A\cap B)

P(A\cup B)=0.8+0.5-0.32

P(A\cup B)=1.3-0.32

P(A\cup B)=0.98

Question:4 Evaluate P(A\cup B), if 2P(A)=P(B)=\frac{5}{13} and P(A\mid B)=\frac{2}{5}

Answer:

Given in the question 2P(A)=P(B)=\frac{5}{13} and P(A\mid B)=\frac{2}{5}

We know that:

P ( A | B ) = \frac{p(A\cap B)}{P(B)}

\frac{2}{5} = \frac{p(A\cap B)}{\frac{5}{13}}

\frac{2\times 5}{5\times 13} = p(A\cap B)

p(A\cap B)=\frac{2}{ 13}

Use, p(A\cup B)=p(A)+p(B)-p(A\cap B)

p(A\cup B)=\frac{5}{26}+\frac{5}{13}-\frac{2}{13}

p(A\cup B)=\frac{11}{26}

Question:5 If P(A)=\frac{6}{11},P(B)=\frac{5}{11} and P(A\cup B)=\frac{7}{11}. , find

(i) P(A\cap B)

Answer:

Given in the question

P(A)=\frac{6}{11},P(B)=\frac{5}{11} and P(A\cup B)=\frac{7}{11}.

By using formula:

p(A\cup B)=p(A)+p(B)-p(A\cap B)

\frac{7}{11}=\frac{6}{11}+\frac{5}{11}-p(A\cap B)

p(A\cap B)=\frac{11}{11}-\frac{7}{11}

p(A\cap B)=\frac{4}{11}

Question:5 If P(A)=\frac{6}{11},P(B)=\frac{5}{11} and P(A\cup B)=\frac{7}{11}, find

(ii) P(A\mid B)

Answer:

It is given that - P(A)=\frac{6}{11},P(B)=\frac{5}{11}

p(A\cap B)=\frac{4}{11}

We know that:

P ( A | B ) = \frac{p(A\cap B)}{P(B)}

P ( A | B ) = \frac{\frac{4}{11}}{\frac{5}{11}}

P ( A | B ) = \frac{4}{5}

Question:5 If P(A)=\frac{6}{11},P(B)=\frac{5}{11} and P(A\cup B)=\frac{7}{11}, find

(iii) P(B\mid A)

Answer:

Given in the question-

P(A)=\frac{6}{11},P(B)=\frac{5}{11} and p(A\cap B)=\frac{4}{11}

Use formula

P ( B | A ) = \frac{p(A\cap B)}{P(A)}

P ( B | A ) = \frac{\frac{4}{11}}{\frac{6}{11}}

P ( B | A ) = \frac{4}{6}=\frac{2}{3}

Question:6 A coin is tossed three times, where

(i)E : head on third toss ,F : heads on first two tosses

Answer:

The sample space S when a coin is tossed three times is

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

It can be seen that the sample space (S) has 8 elements.

Total number of outcomes =2^{3}=8

According to question

E: head on third toss, F: heads on first two tosses

E=\left \{ {HHH},{TTH},{HTH},{THH} \right \}

F=\left \{ {HHH},{HHT} \right \}

E\cap F =HHH

P(F)=\frac{2}{8}=\frac{1}{4}

P(E\cap F)=\frac{1}{8}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{1}{8}}{\frac{1}{4}}

P(E| F)=\frac{4}{8}=\frac{1}{2}

Question:6 A coin is tossed three times, where

(ii)E : at least two heads ,F : at most two heads

Answer:

The sample space S when a coin is tossed three times is

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

It can be seen that the sample space (S) has 8 elements.

Total number of outcomes =2^{3}=8

According to question

E : at least two heads , F : at most two heads

E=\left \{ {HHH},{HTH},{THH},{HHT}\right \}=4

F=\left \{ {HTH},{HHT},{THH},{TTT},{HTT},{TTH},{THT} \right \}=7

E\cap F =\left \{ {HTH},THH,HHT\right \}=3

P(F)=\frac{7}{8}

P(E\cap F)=\frac{3}{8}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{3}{8}}{\frac{7}{8}}

P(E| F)=\frac{3}{7}

Question:6 A coin is tossed three times, where

(iii)E : at most two tails ,F : at least one tail

Answer:

The sample space S when a coin is tossed three times is

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

It can be seen that the sample space (S) has 8 elements.

Total number of outcomes =2^{3}=8

According to question

E: at most two tails, F: at least one tail

E=\left \{ {HHH},{TTH},{HTH},{THH},THT,HTT,HHT \right \}=7

F=\left \{ {TTT},{TTH},{HTH},{THH},THT,HTT,HHT \right \}=7

E\cap F=\left \{ {TTH},{HTH},{THH},THT,HTT,HHT \right \}=6

P(F)=\frac{7}{8}

P(E\cap F)=\frac{6}{8}=\frac{3}{4}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{3}{4}}{\frac{7}{8}}

P(E| F)=\frac{6}{7}

Question:7 Two coins are tossed once, where

(i) E : tail appears on one coin, F : one coin shows head

Answer:

E : tail appears on one coin, F : one coin shows head

Total outcomes =4

E=\left \{ HT,TH \right \}=2

F=\left \{ HT,TH \right \}=2

E\cap F=\left \{ HT,TH \right \}=2

P(F)=\frac{2}{4}=\frac{1}{2}

P(E\cap F)=\frac{2}{4}=\frac{1}{2}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{1}{2}}{\frac{1}{2}}

P(E| F)=1

Question:7 Two coins are tossed once, where

(ii)E : no tail appears,F : no head appears

Answer:

E : no tail appears, F : no head appears

Total outcomes =4

\\E={HH}\\F={TT}

E\cap F=\phi

n(E\cap F)=0

P(F)=1

P(E\cap F)=\frac{0}{4}=0

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{0}{1}=0

Question:8 A die is thrown three times,

E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses

Answer:

E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses

Total outcomes =6^{3}=216

E=\left \{ 114,124,134,144,154,164,214,224,234,244,254,264,314,324,334,344,354,364,414,424,434,454,464,514,524,534,544,554,564,614,624,634,644,654,664 \right \} n(E)=36

F=\left \{ 651,652,653,654,655,656 \right \}

n(F)=6

E\cap F=\left \{ 654 \right \}

n(E\cap F)=1

P(E\cap F)=\frac{1}{216}

P( F)=\frac{6}{216}=\frac{1}{36}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{1}{216}}{\frac{1}{36}}

P(E| F)=\frac{1}{6}

Question:9 Mother, father and son line up at random for a family picture

E : son on one end, F : father in middle

Answer:

E : son on one end, F : father in middle

Total outcomes =3!=3\times 2=6

Let S be son, M be mother and F be father.

Then we have,

E= \left \{ SMF,SFM,FMS,MFS \right \}

n(E)=4

F=\left \{ SFM,MFS \right \}

n(F)=2

E\cap F=\left \{ SFM,MFS \right \}

n(E\cap F)=2

P(F)=\frac{2}{6}=\frac{1}{3}

P(E\cap F)=\frac{2}{6}=\frac{1}{3}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{1}{3}}{\frac{1}{3}}

P(E| F)=1

Question:10 A black and a red dice are rolled.

(a) Find the conditional probability of obtaining a sum greater than 9 , given that the black die resulted in a 5.

Answer:

A black and a red dice are rolled.

Total outcomes =6^{2}=36

Let the A be event obtaining a sum greater than 9 and B be a event that the black die resulted in a 5.

A=\left \{ 46,55,56,64,65,66 \right \}

n(A)=6

B=\left \{ 51,52,53,54,55,56 \right \}

n(B)=6

A\cap B=\left \{ 55,56 \right \}

n(A\cap B)=2

P(A\cap B)=\frac{2}{36}

P( B)=\frac{6}{36}

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{\frac{2}{36}}{\frac{6}{36}}=\frac{2}{6}=\frac{1}{3}

Question:10 A black and a red dice are rolled.

(b) Find the conditional probability of obtaining the sum 8 , given that the red die resulted in a number less than 4 .

Answer:

A black and a red dice are rolled.

Total outcomes =6^{2}=36

Let the A be event obtaining a sum 8 and B be a event thatthat the red die resulted in a number less than 4 .

A=\left \{ 26,35,53,44,62, \right \}

n(A)=5

Red dice is rolled after black dice.

B=\left \{ 11,12,13,21,22,23,31,32,33,41,42,43,51,52,53,61,62,63 \right \}

n(B)=18

A\cap B=\left \{ 53,62 \right \}

n(A\cap B)=2

P(A\cap B)=\frac{2}{36}

P( B)=\frac{18}{36}

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{\frac{2}{36}}{\frac{18}{36}}=\frac{2}{18}=\frac{1}{9}

Question:11 A fair die is rolled. Consider events E=\left \{ 1,3,5 \right \},F\left \{ 2,3 \right \} and G=\left \{ 2,3,4,5 \right \} Find

(i) P(E\mid F) and P(F\mid E)

Answer:

A fair die is rolled.

Total oucomes =\left \{ 1,2,3,4,5,6 \right \}=6

E=\left \{ 1,3,5 \right \},F\left \{ 2,3 \right \}

E\cap F=\left \{ 3\right \}

n(E\cap F)=1

n( F)=2

n( E)=3

P( E)=\frac{3}{6} P( F)=\frac{2}{6} and P(E\cap F)=\frac{1}{6}

P(E| F)=\frac{P(E\cap F)}{P(F)}

P(E| F)=\frac{\frac{1}{6}}{\frac{2}{6}}

P(E| F)=\frac{1}{2}

P(F| E)=\frac{P(F\cap E)}{P(E)}

P(F| E)=\frac{\frac{1}{6}}{\frac{3}{6}}

P(F| E)=\frac{1}{3}

Question:11 A fair die is rolled. Consider events E=\left \{ 1,3,5 \right \},F=\left \{ 2,3 \right \} and G=\left \{ 2,3,4,5 \right \} Find

(ii) P(E\mid G) and P(G\mid E)

Answer:

A fair die is rolled.

Total oucomes =\left \{ 1,2,3,4,5,6 \right \}=6

E=\left \{ 1,3,5 \right \} , G=\left \{ 2,3,4,5 \right \}

E\cap G=\left \{ 3,5\right \}

n(E\cap G)=2

n( G)=4

n( E)=3

P( E)=\frac{3}{6} P( G)=\frac{4}{6} P(E\cap F)=\frac{2}{6}

P(E| G)=\frac{P(E\cap G)}{P(G)}

P(E| G)=\frac{\frac{2}{6}}{\frac{4}{6}}

P(E| G)=\frac{2}{4}=\frac{1}{2}

P(G| E)=\frac{P(G\cap E)}{P(E)}

P(G| E)=\frac{\frac{2}{6}}{\frac{3}{6}}

P(G| E)=\frac{2}{3}

Question:11 A fair die is rolled. Consider events E=\left \{ 1,3,5 \right \},F=\left \{ 2,3 \right \} and G=\left \{ 2,3,4,5 \right \} Find

(iii) P((E\cup F)\mid G) and P((E\cap F)\mid G)

Answer:

A fair die is rolled.

Total oucomes =\left \{ 1,2,3,4,5,6 \right \}=6

E=\left \{ 1,3,5 \right \},F\left \{ 2,3 \right \} and G=\left \{ 2,3,4,5 \right \}

E\cap G=\left \{ 3,5 \right \} , F\cap G=\left \{ 2,3\right \}

(E\cap G)\cap G =\left \{ 3 \right \}

P[(E\cap G)\cap G] =\frac{1}{6} P(E\cap G) =\frac{2}{6} P(F\cap G) =\frac{2}{6}

P((E\cup F)|G) = P(E|G)+P(F|G) - P[(E\cap F)|G]

=\frac{P(E\cap G)}{P(G)}+\frac{P(F\cap G)}{P(G)}-\frac{P((E\cap F)\cap G)}{P(G)}

=\frac{\frac{2}{6}}{\frac{4}{6}}+\frac{\frac{2}{6}}{\frac{4}{6}}-\frac{\frac{1}{6}}{\frac{4}{6}}

=\frac{2}{4}+\frac{2}{4}-\frac{1}{4}

=\frac{3}{4}

P((E\cap F)|G)=\frac{P((E\cap F)\cap G)}{P(G)}

P((E\cap F)|G)=\frac{\frac{1}{6}}{\frac{4}{6}}

P((E\cap F)|G)=\frac{1}{4}

Question:12 Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that

(i) the youngest is a girl,

Answer:

Assume that each born child is equally likely to be a boy or a girl.

Let first and second girl are denoted by G1\, \, \, and \, \, \,G2 respectively also first and second boy are denoted by B1\, \, \, and \, \, \,B2

If a family has two children, then total outcomes =2^{2}=4 =\left \{ (B1B2),(G1G2),(G1B2),(G2B1)\right \}

Let A= both are girls =\left \{(G1G2)\right \}

and B= the youngest is a girl = =\left \{(G1G2),(B1G2)\right \}

A\cap B=\left \{(G1G2)\right \}

P(A\cap B)=\frac{1}{4} P( B)=\frac{2}{4}

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{\frac{1}{4}}{\frac{2}{4}}

P(A| B)=\frac{1}{2}

Therefore, the required probability is 1/2

Question:12 Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that

(ii) at least one is a girl?

Answer:

Assume that each born child is equally likely to be a boy or a girl.

Let first and second girl are denoted by G1\, \, \, and \, \, \,G2 respectively also first and second boy are denoted by B1\, \, \, and \, \, \,B2

If a family has two children, then total outcomes =2^{2}=4 =\left \{ (B1B2),(G1G2),(G1B2),(G2B1)\right \}

Let A= both are girls =\left \{(G1G2)\right \}

and C= at least one is a girl = =\left \{(G1G2),(B1G2),(G1B2)\right \}

A\cap B=\left \{(G1G2)\right \}

P(A\cap B)=\frac{1}{4} P( C)=\frac{3}{4}

P(A| C)=\frac{P(A\cap C)}{P(C)}

P(A| C)=\frac{\frac{1}{4}}{\frac{3}{4}}

P(A| C)=\frac{1}{3}

Question:13 An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?

Answer:

An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions.

Total number of questions =300+200+500+400=1400

Let A = question be easy.

n(A)= 300+500=800

P(A)=\frac{800}{1400}=\frac{8}{14}

Let B = multiple choice question

n(B)=500+400=900

P(B)=\frac{900}{1400}=\frac{9}{14}

A\cap B = easy multiple questions

n(A\cap B) =500

P(A\cap B) =\frac{500}{1400}=\frac{5}{14}

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{\frac{5}{14}}{\frac{9}{14}}

P(A| B)=\frac{5}{9}

Therefore, the required probability is 5/9

Question:14 Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.

Answer:

Two dice are thrown.

Total outcomes =6^2=36

Let A be the event ‘the sum of numbers on the dice is 4.

A=\left \{ (13),\left ( 22 \right ),(31) \right \}

Let B be the event that two numbers appearing on throwing two dice are different.

B=\left \{ (12),(13),(14),(15),(16),(21)\left ( 23 \right ),(24),(25),(26,)(31),(32),(34),(35),(36),(41),(42),(43),(45),(46),(51),(52),(53),(54),(56) ,(61),(62),(63),(64),(65)\right \} n(B)=30

P(B)=\frac{30}{36}

A\cap B=\left \{ (13),(31) \right \}

n(A\cap B)=2

P(A\cap B)=\frac{2}{36}

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{\frac{2}{36}}{\frac{30}{36}}

P(A| B)=\frac{2}{30}=\frac{1}{15}

Therefore, the required probability is 1/15

Question:15 Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.

Answer:

Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin.

Total outcomes =\left \{ (1H),(1T),(2H),(2T),(31),(32),(33),(34),(35),(36),(4H),(4T),(5H),(5T),(61),(62),(63),(64),(65),(66)\right \}

Total number of outcomes =20

Let A be a event when coin shows a tail.

A=\left \{ ((1T),(2T),(4T),(5T)\right \}

Let B be a event that ‘at least one die shows a 3’.

B=\left \{ (31),(32),(33),(34),(35),(36),(63)\right \}

n(B)=7

P(B)=\frac{7}{20}

A\cap B= \phi

n(A\cap B)= 0

P(A\cap B)= \frac{0}{20}=0

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{0}{\frac{7}{20}}

P(A| B)=0

Question:16 In the following Exercise 16 choose the correct answer:

If P(A)=\frac{1}{2},P(B)=0, then P(A\mid B) is

(A) 0

(B) \frac{1}{2}

(C) not\; defined

(D) 1

Answer:

It is given that

P(A)=\frac{1}{2},P(B)=0,

P(A| B)=\frac{P(A\cap B)}{P(B)}

P(A| B)=\frac{P(A\cap B)}{0}

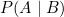Hence, P(A\mid B) is not defined .

Thus, correct option is C.

Question:17 In the following Exercise 17 choose the correct answer:

If A and B are events such that P(A\mid B)=P(B\mid A), then

(A) A\subset B but A\neq B

(B) A=B

(C) A\cap B=\psi

(D) P(A)=P(B)

Answer:

It is given that P(A\mid B)=P(B\mid A),

\Rightarrow \frac{P(A\cap B)}{P(B)} =\frac{P(A\cap B)}{P(A)}

\Rightarrow P(A)=P(B)

Hence, option D is correct.


NCERT solutions for class 12 maths chapter 13 probability-Exercise: 13.2

Question:1 If P(A)=\frac{3}{5} and P(B)=\frac{1}{5}, find P(A\cap B) if A and B are independent events.

Answer:

P(A)=\frac{3}{5} and P(B)=\frac{1}{5},

Given : A and B are independent events.

So we have, P(A\cap B)=P(A).P(B)

\Rightarrow \, \, \, \, P(A\cap B)=\frac{3}{5}\times \frac{1}{5}

\Rightarrow \, \, \, \, P(A\cap B)=\frac{3}{25}

Question: 2 Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.

Answer:

Two cards are drawn at random and without replacement from a pack of 52 playing cards.

There are 26 black cards in a pack of 52.

Let P(A) be the probability that first cards is black.

Then, we have

P(A)= \frac{26}{52}=\frac{1}{2}

Let P(B) be the probability that second cards is black.

Then, we have

P(B)= \frac{25}{51}

The probability that both the cards are black =P(A).P(B)

=\frac{1}{2}\times \frac{25}{51}

=\frac{25}{102}

Question:3 A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.

Answer:

Total oranges = 15

Good oranges = 12

Bad oranges = 3

Let P(A) be the probability that first orange is good.

The, we have

P(A)= \frac{12}{15}=\frac{4}{5}

Let P(B) be the probability that second orange is good.

P(B)=\frac{11}{14}

Let P(C) be the probability that third orange is good.

P(C)=\frac{10}{13}

The probability that a box will be approved for sale =P(A).P(B).P(C)

=\frac{4}{5}.\frac{11}{14}.\frac{10}{13}

=\frac{44}{91}

Question:4 A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B are independent events or not.

Answer:

A fair coin and an unbiased die are tossed,then total outputs are:

= \left \{ (H1),(H2),(H3),(H4),(H5),(H6),(T1),(T2),(T3),(T4),(T5),(T6) \right \}

=12

A is the event ‘head appears on the coin’ .

Total outcomes of A are : = \left \{ (H1),(H2),(H3),(H4),(H5),(H6) \right \}

P(A)=\frac{6}{12}=\frac{1}{2}

B is the event ‘3 on the die’.

Total outcomes of B are : = \left \{ (T3),(H3)\right \}

P(B)=\frac{2}{12}=\frac{1}{6}

\therefore A\cap B = (H3)

P (A\cap B) = \frac{1}{12}

Also, P (A\cap B) = P(A).P(B)

P (A\cap B) = \frac{1}{2}\times \frac{1}{6}=\frac{1}{12}

Hence, A and B are independent events.

Question:5 A die marked 1,2,3 in red and 4,5,6 in green is tossed. Let A be the event, ‘the number is even,’ and B be the event, ‘the number is red’. Are A and B independent?

Answer:

Total outcomes =\left \{ 1,2,3,4,5,6 \right \}=6 .

A is the event, ‘the number is even,’

Outcomes of A =\left \{ 2,4,6 \right \}

n(A)=3.

P(A)=\frac{3}{6}=\frac{1}{2}

B is the event, ‘the number is red’.

Outcomes of B =\left \{ 1,2,3 \right \}

n(B)=3.

P(B)=\frac{3}{6}=\frac{1}{2}

\therefore (A\cap B)=\left \{ 2 \right \}

n(A\cap B)=1

P(A\cap B)=\frac{1}{6}

Also,

P(A\cap B)=P(A).P(B)

P(A\cap B)=\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}\neq \frac{1}{6}

Thus, both the events A and B are not independent.

Question:6 Let E and F be events with P(E)=\frac{3}{5},P(F)=\frac{3}{10} and P(E\cap F)=\frac{1}{5}. Are E and F independent?

Answer:

Given :

P(E)=\frac{3}{5},P(F)=\frac{3}{10} and P(E\cap F)=\frac{1}{5}.

For events E and F to be independent , we need

P(E\cap F)=P(E).P(F)

P(E\cap F)=\frac{3}{5}\times \frac{3}{10}=\frac{9}{50}\neq \frac{1}{5}

Hence, E and F are not indepent events.

Question:7 Given that the events A and B are such that P(A)=\frac{1}{2},P(A\cup B)=\frac{3}{5} and P(B)=p. Find p if they are

(i) mutually exclusive

Answer:

Given,

P(A)=\frac{1}{2},P(A\cup B)=\frac{3}{5}

Also, A and B are mutually exclusive means A\cap B=\phi .

P(A\cup B)=P(A)+P(B)-P(A\cap B)

\frac{3}{5}=\frac{1}{2}+P(B)-0

P(B)=\frac{3}{5}-\frac{1}{2}=\frac{1}{10}

Question:7 Given that the events A and B are such that P(A)=12,P(A\cup B)=\frac{3}{5} and P(B)=p. Find p if they are

(ii) independent

Answer:

Given,

P(A)=\frac{1}{2},P(A\cup B)=\frac{3}{5}

Also, A and B are independent events means

P(A\cap B) = P(A).P(B) . Also P(B)=p.

P(A\cap B) = P(A).P(B)=\frac{p}{2}

P(A\cup B)=P(A)+P(B)-P(A\cap B)

\frac{3}{5}=\frac{1}{2}+p-\frac{p}{2}

\frac{p}{2}=\frac{3}{5}-\frac{1}{2}=\frac{1}{10}

p=\frac{2}{10}=\frac{1}{5}

Question:8 Let A and B be independent events with P(A)=0.3 and P(B)=0.4 Find

(i) P(A\cap B)

Answer:

P(A)=0.3 and P(B)=0.4

Given : A and B be independent events

So, we have

P(A\cap B)=P(A).P(B)

P(A\cap B)=0.3\times 0.4=0.12

Question:8 Let A and B be independent events with P(A)=0.3 and P(B)=0.4 Find

(ii) P(A\cup B)

Answer:

P(A)=0.3 and P(B)=0.4

Given : A and B be independent events

So, we have

P(A\cap B)=P(A).P(B)

P(A\cap B)=0.3\times 0.4=0.12

We have, P(A\cup B)=P(A)+P(B)-P(A\cap B)

P(A\cup B)=0.3+0.4-0.12=0.58

Question:8 Let A and B be independent events with P(A)=0.3 and P(B)=0.4 Find

(iii) P(A\mid B)

Answer:

P(A)=0.3 and P(B)=0.4

Given : A and B be independent events

So, we have P(A\cap B)=0.12

P(A|B)=\frac{P(A\cap B)}{P(B)}

P(A|B)=\frac{0.12}{0.4}= 0.3

Question:8 Let A and B be independent events with P(A)=0.3 and P(B)=0.4 Find

(iv) P(B\mid A)

Answer:

P(A)=0.3 and P(B)=0.4

Given : A and B be independent events

So, we have P(A\cap B)=0.12

P(B|A)=\frac{P(A\cap B)}{P(A)}

P(B|A)=\frac{0.12}{0.3}= 0.4

Question:9 If A and B are two events such that P(A)=\frac{1}{4},P(B)=\frac{1}{2} and P(A\cap B)=\frac{1}{8}, find P(not\; A\; and\; not\; B).

Answer:

If A and B are two events such that P(A)=\frac{1}{4},P(B)=\frac{1}{2} and P(A\cap B)=\frac{1}{8},

P(not\; A\; and\; not\; B)= P(A'\cap B')

P(not\; A\; and\; not\; B)= P(A\cup B)' use, (P(A'\cap B')= P(A\cup B)')

= 1-(P(A)+P(B)-P(A\cap B))

= 1-(\frac{1}{4}+\frac{1}{2}-\frac{1}{8})

= 1-(\frac{6}{8}-\frac{1}{8})

= 1-\frac{5}{8}

= \frac{3}{8}

Question:10 Events A and B are such that P(A)=\frac{1}{2},P(B)=\frac{7}{12} and P(not \; A \; or\; not\; B)=\frac{1}{4}. State whether A and B are independent ?

Answer:

If A and B are two events such that P(A)=\frac{1}{2},P(B)=\frac{7}{12} and P(not \; A \; or\; not\; B)=\frac{1}{4}.

P(A'\cup B')=\frac{1}{4}

P(A\cap B)'=\frac{1}{4} (A'\cup B'=(A\cap B)')

\Rightarrow \, \, 1-P(A\cap B)=\frac{1}{4}

\Rightarrow \, \, \, P(A\cap B)=1-\frac{1}{4}=\frac{3}{4}

Also \, \, \, P(A\cap B)=P(A).P(B)

P(A\cap B)=\frac{1}{2}\times \frac{7}{12}=\frac{7}{24}

As we can see \frac{3}{4}\neq \frac{7}{24}

Hence, A and B are not independent.

Question:11 Given two independent events A and B such that P(A)=0.3,P(B)=0.6, Find

(i) P(A \; and\; B)

Answer:

P(A)=0.3,P(B)=0.6,

Given two independent events A and B .

P(A\cap B)=P(A).P(B)

P(A\cap B)=0.3\times 0.6=0.18

Also , we know P(A \, and \, B)=P(A\cap B)=0.18

Question:11 Given two independent events A and B such that P(A)=0.3,P(B)=0.6, Find

(ii) P(A \; and \; not\; B)

Answer:

P(A)=0.3,P(B)=0.6,

Given two independent events A and B .

P(A \; and \; not\; B) =P(A)-P(A\cap B)

=0.3-0.18=0.12

Question:11 Given two independent events A and B such that P(A)=0.3,P(B)0.6, Find

(iii) P(A\; or \; B)

Answer:

P(A)=0.3,P(B)=0.6,

P(A\cap B)=0.18

P(A\; or \; B)=P(A\cup B)

P(A\cup B)=P(A)+P(B)-P(A\cap B)

=0.3+0.6-0.18

=0.9-0.18

=0.72

Question:11 Given two independent events A and B such that P(A)=0.3,P(B)=0.6, Find

(iv) P(neither\; A\; nor\; B)

Answer:

P(A)=0.3,P(B)=0.6,

P(A\cap B)=0.18

P(A\; or \; B)=P(A\cup B)

P(A\cup B)=P(A)+P(B)-P(A\cap B)

=0.3+0.6-0.18

=0.9-0.18

=0.72

P(neither\; A\; nor\; B) =P(A'\cap B')

= P((A\cup B)')

=1-P(A\cup B)

=1-0.72

=0.28

Question:12 A die is tossed thrice. Find the probability of getting an odd number at least once.

Answer:

A die is tossed thrice.

Outcomes =\left \{ 1,2,3,4,5,6 \right \}

Odd numbers =\left \{ 1,3,5 \right \}

The probability of getting an odd number at first throw

=\frac{3}{6}=\frac{1}{2}

The probability of getting an even number

=\frac{3}{6}=\frac{1}{2}

Probability of getting even number three times

=\frac{1}{2}\times \frac{1}{2}\times \frac{1}{2}=\frac{1}{8}

The probability of getting an odd number at least once = 1 - the probability of getting an odd number in none of throw

= 1 - probability of getting even number three times

=1-\frac{1}{8}

=\frac{7}{8}

Question:13 Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that

(i) both balls are red.

Answer:

Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.

Total balls =18

Black balls = 10

Red balls = 8

The probability of getting a red ball in first draw

=\frac{8}{18}=\frac{4}{9}

The ball is repleced after drawing first ball.

The probability of getting a red ball in second draw

=\frac{8}{18}=\frac{4}{9}

the probability that both balls are red

=\frac{4}{9}\times \frac{4}{9}=\frac{16}{81}

Question:13 Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that

(ii) first ball is black and second is red.

Answer:

Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.

Total balls =18

Black balls = 10

Red balls = 8

The probability of getting a black ball in the first draw

=\frac{10}{18}=\frac{5}{9}

The ball is replaced after drawing the first ball.

The probability of getting a red ball in the second draw

=\frac{8}{18}=\frac{4}{9}

the probability that the first ball is black and the second is red

=\frac{5}{9}\times \frac{4}{9}=\frac{20}{81}

Question:13 Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that

(iii) one of them is black and other is red.

Answer:

Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.

Total balls =18

Black balls = 10

Red balls = 8

Let the first ball is black and the second ball is red.

The probability of getting a black ball in the first draw

=\frac{10}{18}=\frac{5}{9}

The ball is replaced after drawing the first ball.

The probability of getting a red ball in the second draw

=\frac{8}{18}=\frac{4}{9}

the probability that the first ball is black and the second is red

=\frac{5}{9}\times \frac{4}{9}=\frac{20}{81} ...........................1

Let the first ball is red and the second ball is black.

The probability of getting a red ball in the first draw

=\frac{8}{18}=\frac{4}{9}

The probability of getting a black ball in the second draw

=\frac{10}{18}=\frac{5}{9}

the probability that the first ball is red and the second is black

=\frac{4}{9}\times \frac{5}{9}=\frac{20}{81} ...........................2

Thus,

The probability that one of them is black and the other is red = the probability that the first ball is black and the second is red + the probability that the first ball is red and the second is black =\frac{20}{81}+\frac{20}{81}=\frac{40}{81}

Question:14 Probability of solving specific problem independently by A and B are \frac{1}{2} and \frac{1}{3} respectively. If both try to solve the problem independently, find the probability that

(i) the problem is solved

Answer:

P(A)=\frac{1}{2} and P(B)=\frac{1}{3}

Since, problem is solved independently by A and B,

\therefore P(A\cap B)=P(A).P(B)

P(A\cap B)=\frac{1}{2}\times \frac{1}{3}

P(A\cap B)=\frac{1}{6}

probability that the problem is solved = P(A\cup B)

P(A\cup B)=P(A)+P(B)-P(A\cap B)

P(A\cup B)=\frac{1}{2}+\frac{1}{3}-\frac{1}{6}

P(A\cup B)=\frac{5}{6}-\frac{1}{6}

P(A\cup B)=\frac{4}{6}=\frac{2}{3}

Question:14 Probability of solving specific problem independently by A and B are \frac{1}{2} and \frac{1}{3} respectively. If both try to solve the problem independently, find the probability that

(ii) exactly one of them solves the problem

Answer:

P(A)=\frac{1}{2} and P(B)=\frac{1}{3}

P(A')=1-P(A) , P(B')=1-P(B)

P(A')=1-\frac{1}{2}=\frac{1}{2} , P(B')=1-\frac{1}{3}=\frac{2}{3}

probability that exactly one of them solves the problem =P(A\cap B') + P(A'\cap B)

probability that exactly one of them solves the problem =P(A).P(B')+P(A')P(B)

=\frac{1}{2}\times \frac{2}{3}+\frac{1}{2}\times \frac{1}{3}

= \frac{2}{6}+\frac{1}{6}

= \frac{3}{6}=\frac{1}{2}

Question:15 One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent ?

(i) E : ‘the card drawn is a spade’

F : ‘the card drawn is an ace’

Answer:

One card is drawn at random from a well shuffled deck of 52 cards

Total ace = 4

total spades =13

E : ‘the card drawn is a spade

F : ‘the card drawn is an ace’

P(E)=\frac{13}{52}=\frac{1}{4}

P(F)=\frac{4}{52}=\frac{1}{13}

E\cap F : a card which is spade and ace = 1

P(E\cap F)=\frac{1}{52}

P(E).P(F)=\frac{1}{4}\times \frac{1}{13}=\frac{1}{52}

\Rightarrow P(E\cap F)=P(E).P(F)=\frac{1}{52}

Hence, E and F are indepentdent events .

Question:15 One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent ?

(ii) E : ‘the card drawn is

F : ‘the card drawn is a king’

Answer:

One card is drawn at random from a well shuffled deck of 52 cards

Total black card = 26

total king =4

E : ‘the card drawn is black’

F : ‘the card drawn is a king’

P(E)=\frac{26}{52}=\frac{1}{2}

P(F)=\frac{4}{52}=\frac{1}{13}

E\cap F : a card which is black and king = 2

P(E\cap F)=\frac{2}{52}=\frac{1}{26}

P(E).P(F)=\frac{1}{2}\times \frac{1}{13}=\frac{1}{26}

\Rightarrow P(E\cap F)=P(E).P(F)=\frac{1}{26}

Hence, E and F are indepentdent events .

Question:15 One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent ?

(iii) E : ‘the card drawn is a king or queen’

F : ‘the card drawn is a queen or jack’.

Answer:

One card is drawn at random from a well shuffled deck of 52 cards

Total king or queen = 8

total queen or jack = 8

E : ‘the card drawn is a king or queen’

F : ‘the card drawn is a queen or jack’.

P(E)=\frac{8}{52}=\frac{2}{13}

P(F)=\frac{8}{52}=\frac{2}{13}

E\cap F : a card which is queen = 4

P(E\cap F)=\frac{4}{52}=\frac{1}{13}

P(E).P(F)=\frac{2}{13}\times \frac{2}{13}=\frac{4}{169}

\Rightarrow P(E\cap F)\neq P(E).P(F)

Hence, E and F are not indepentdent events

Question:16 In a hostel, 60\; ^{o}/_{o} of the students read Hindi newspaper, 40\; ^{o}/_{o} read English newspaper and 20\; ^{o}/_{o} read both Hindi and English newspapers. A student is selected at random.

(a) Find the probability that she reads neither Hindi nor English newspapers

Answer:

H : 60\; ^{o}/_{o} of the students read Hindi newspaper,

E : 40\; ^{o}/_{o} read English newspaper and

H \cap E : 20\; ^{o}/_{o} read both Hindi and English newspapers.

P(H)=\frac{60}{100}=\frac{6}{10}=\frac{3}{5}

P(E)=\frac{40}{100}=\frac{4}{10}=\frac{2}{5}

P(H\cap E)=\frac{20}{100}=\frac{2}{10}=\frac{1}{5}

the probability that she reads neither Hindi nor English newspapers =1-P(H\cup E)

=1-(P(H)+P(E)-P(H\cap E))

=1-(\frac{3}{5}+\frac{2}{5}-\frac{1}{5})

=1-\frac{4}{5}

=\frac{1}{5}

Question:16 In a hostel, 60\; ^{o}/_{o} of the students read Hindi newspaper, 40\; ^{o}/_{o} read English newspaper and 20\; ^{o}/_{o} read both Hindi and English newspapers. A student is selected at random.

(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.

Answer:

H : 60\; ^{o}/_{o} of the students read Hindi newspaper,

E : 40\; ^{o}/_{o} read English newspaper and

H \cap E : 20\; ^{o}/_{o} read both Hindi and English newspapers.

P(H)=\frac{60}{100}=\frac{6}{10}=\frac{3}{5}

P(E)=\frac{40}{100}=\frac{4}{10}=\frac{2}{5}

P(H\cap E)=\frac{20}{100}=\frac{2}{10}=\frac{1}{5}

The probability that she reads English newspape if she reads Hindi newspaper =P(E|H)

P(E|H)=\frac{P(E\cap H)}{P(H)}

P(E|H)=\frac{\frac{1}{5}}{\frac{3}{5}}

P(E|H)=\frac{1}{3}

Question:16 In a hostel, 60^{o}/_{o} of the students read Hindi newspaper, 40^{o}/_{o} read English newspaper and 20^{o}/_{o} read both Hindi and English newspapers. A student is selected at random.

(c) If she reads English newspaper, find the probability that she reads Hindi newspaper.

Answer:

H : 60\; ^{o}/_{o} of the students read Hindi newspaper,

E : 40\; ^{o}/_{o} read English newspaper and

H \cap E : 20\; ^{o}/_{o} read both Hindi and English newspapers.

P(H)=\frac{60}{100}=\frac{6}{10}=\frac{3}{5}

P(E)=\frac{40}{100}=\frac{4}{10}=\frac{2}{5}

P(H\cap E)=\frac{20}{100}=\frac{2}{10}=\frac{1}{5}

the probability that she reads Hindi newspaper if she reads English newspaper = P(H |E)

P(H |E)=\frac{P(H\cap E)}{P(E)}

P(H |E)=\frac{\frac{1}{5}}{\frac{2}{5}}

P(H |E)=\frac{1}{2}

Question:17 The probability of obtaining an even prime number on each die, when a pair of dice is rolled is

(A) 0

(B) \frac{1}{3}

(C) \frac{1}{12}

(D) \frac{1}{36}

Answer:

when a pair of dice is rolled, total outcomes =6^2=36

Even prime number =\left \{ 2 \right \}

n(even \, \, prime\, \, number)=1

The probability of obtaining an even prime number on each die =P(E)

P(E)=\frac{1}{36}

Option D is correct.

Question:18 Two events A and B will be independent, if

(A) A and B are mutually exclusive

(B) P(A'B')=\left [ 1-P(A) \right ]\left [ 1-P(B) \right ]

(C) P(A)=P(B)

(D) P(A)+P(B)=1

Answer:

Two events A and B will be independent, if

P(A\cap B)=P(A).P(B)

Or P(A'\cap B')=P(A'B')=P(A').P(B')=(1-P(A)).(1-P(B))

Option B is correct.


NCERT solutions for class 12 maths chapter 13 probability-Exercise: 13.3

Question:1 An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red?

Answer:

Black balls = 5

Red balls = 5

Total balls = 10

CASE 1 Let red ball be drawn in first attempt.

P(drawing\, red\, ball)=\frac{5}{10}=\frac{1}{2}

Now two red balls are added in urn .

Now red balls = 7, black balls = 5

Total balls = 12

P(drawing\, red\, ball)=\frac{7}{12}

CASE 2

Let black ball be drawn in first attempt.

P(drawing\, black\, ball)=\frac{5}{10}=\frac{1}{2}

Now two black balls are added in urn .

Now red balls = 5, black balls = 7

Total balls = 12

P(drawing\, red\, ball)=\frac{5}{12}

the probability that the second ball is red =

=\frac{1}{2}\times \frac{7}{12}+\frac{1}{2}\times \frac{5}{12}

= \frac{7}{24}+ \frac{5}{24}

= \frac{12}{24}=\frac{1}{2}

Question:2 A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn frome bag which is found to be red. Find the probability that the ball is drawn from the first bag.

Answer:

BAG 1 : Red balls =4 Black balls=4 Total balls = 8

BAG 2 : Red balls = 2 Black balls = 6 Total balls = 8

B1 : selecting bag 1

B2 : selecting bag 2

P(B1)=P(B2)=\frac{1}{2}

Let R be a event of getting red ball

P(R|B1) = P(drawing\, \, red\, \, ball\, \, from \, first \, \, bag)= \frac{4}{8}=\frac{1}{2}

P(R|B2) = P(drawing\, \, red\, \, ball\, \, from \, second \, \, bag)= \frac{2}{8}=\frac{1}{4}

probability that the ball is drawn from the first bag,

given that it is red is P(B1|R) .

Using Baye's theorem, we have

P(B1|R) = \frac{P(B1).P(R|B1)}{P(B1).P(R|B1)+P(B2).P(R|B2)}

P(B1|R) = \frac{\frac{1}{2}\times \frac{1}{2}}{\frac{1}{2}\times \frac{1}{2}+\frac{1}{2}\times \frac{1}{4}}

P(B1|R) =\frac{\frac{1}{4}}{\frac{1}{4}+\frac{1}{8}}

P(B1|R) =\frac{\frac{1}{4}}{\frac{3}{8}}

P(B1|R) = \frac{2}{3}

Question:3 Of the students in a college, it is known that 60^{o}/_{o} reside in hostel and 40^{o}/_{o} are day scholars (not residing in hostel). Previous year results report that 30^{o}/_{o} of all students who reside in hostel attain A grade and 20^{o}/_{o} of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostlier?

Answer:

H : reside in hostel

D : day scholars

A : students who attain grade A

P(H)=\frac{60}{100}=\frac{6}{10}=\frac{3}{5}

P(D)=\frac{40}{100}=\frac{4}{10}=\frac{2}{5}

P(A|H)=\frac{30}{100}=\frac{3}{10}

P(A|D)=\frac{20}{100}=\frac{2}{10}= \frac{1}{5}

By Bayes theorem :

P(H|A)=\frac{P(H).P(A|H)}{P(H).P(A|H)+P(D).P(A|D)}

P(H|A)=\frac{\frac{3}{5}\times \frac{3}{10}}{\frac{3}{5}\times \frac{3}{10}+\frac{2}{5}\times \frac{1}{5}}

P(H|A)=\frac{\frac{9}{50}}{\frac{9}{50}+\frac{2}{25}}

P(H|A)=\frac{\frac{9}{50}}{\frac{13}{50}}

P(H|A)=\frac{9}{13}

Question:4 In answering a question on a multiple choice test, a student either knows the answer or guesses. Let \frac{3}{4} be the probability that he knows the answer and \frac{1}{4} be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability \frac{1}{4} . What is the probability that the student knows the answer given that he answered it correctly?

Answer:

A : Student knows answer.

B : Student guess the answer

C : Answer is correct

P(A)=\frac{3}{4} P(B)=\frac{1}{4}

P(C|A)=1

P(C|B)=\frac{1}{4}

By Bayes theorem :

P(A|C)=\frac{P(A).P(C|A)}{P(A).P(C|A)+P(B).P(C|B)}

P(A|C)=\frac{\frac{3}{4}\times 1}{\frac{3}{4}\times 1+\frac{1}{4}\times \frac{1}{4}}

=\frac{\frac{3}{4}}{\frac{3}{4}+\frac{1}{16}} =\frac{\frac{3}{4}}{\frac{13}{16}}

P(A|C)=\frac{12}{13}

Question:5 A laboratory blood test is 99^{o}/_{o} effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 0.5^{o}/_{o} of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1^{o}/_{o} of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive ?

Answer:

A : Person selected is having the disease

B : Person selected is not having the disease.

C :Blood result is positive.

P(A)= 0.1 \%=\frac{1}{1000}=0.001

P(B)= 1 -P(A)=1-0.001=0.999

P(C|A)=99\%=0.99

P(C|B)=0.5\%=0.005

By Bayes theorem :

P(A|C)=\frac{P(A).P(C|A)}{P(A).P(C|A)+P(B).P(C|B)}

=\frac{0.001\times 0.99}{0.001\times 0.99+0.999\times 0.005}

=\frac{0.00099}{0.00099+0.004995}

=\frac{0.00099}{0.005985} =\frac{990}{5985}

=\frac{22}{133}

Question:6 There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75^{o}/_{o} of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?

Answer:

Given : A : chossing a two headed coin

B : chossing a biased coin

C : chossing a unbiased coin

P(A)=P(B)=P(C)=\frac{1}{3}

D : event that coin tossed show head.

P(D|A)=1

Biased coin that comes up heads 75^{o}/_{o} of the time.

P(D|B)=\frac{75}{100}=\frac{3}{4}

P(D|C)=\frac{1}{2}

P(B|D)=\frac{P(B).P(D|B)}{P(B).P(D|B)+P(A).P(D|A)+P(C).P(D|C)}

P(B|D)=\frac{\frac{1}{3}\times 1}{\frac{1}{3}\times 1+\frac{1}{3}\times \frac{3}{4}+\frac{1}{3}\times \frac{1}{2}}

P(B|D)=\frac{\frac{1}{3}}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}

P(B|D)=\frac{\frac{1}{3}}{\frac{9}{12}}

P(B|D)={\frac{1\times 12}{3\times 9}}

P(B|D)={\frac{4}{9}}

Question:7 An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01,0.03 , and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?

Answer:

Let A : scooter drivers = 2000

B : car drivers = 4000

C : truck drivers = 6000

Total drivers = 12000

P(A)=\frac{2000}{12000}=\frac{1}{6}=0.16

P(B)=\frac{4000}{12000}=\frac{1}{3}=0.33

P(C)=\frac{6000}{12000}=\frac{1}{2}=0.5

D : the event that person meets with an accident.

P(D|A)= 0.01

P(D|B)= 0.03

P(D|C)= 0.15

P(A|D)=\frac{P(A).P(D|A)}{P(B).P(D|B)+P(A).P(D|A)+P(C).P(D|C)}

P(A|D)= \frac{0.16\times 0.01}{0.16\times 0.01+0.33\times 0.03+0.5\times 0.15}

P(A|D)= \frac{0.0016}{0.0016+0.0099+0.075}

P(A|D)= \frac{0.0016}{0.0865}

P(A|D)= 0.019

Question:8 A factory has two machines A and B. Past record shows that machine A produced 60^{o}/_{o} of the items of output and machine B produced 40^{o}/_{o} of the items. Further, 2^{o}/_{o} of the items produced by machine A and 1^{o}/_{o} produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B ?

Answer:

A : Items produced by machine A =60\%

B : Items produced by machine B =40\%

P(A)= \frac{60}{100}=\frac{3}{5}

P(B)= \frac{40}{100}=\frac{2}{5}

X : Produced item found to be defective.

P(X|A)= \frac{2}{100}=\frac{1}{50}

P(X|B)= \frac{1}{100}

P(B|X)= \frac{P(B).P(X|B)}{P(B).P(X|B)+P(A).P(X|A)}

P(B|X)= \frac{\frac{2}{5}\times \frac{1}{100}}{\frac{2}{5}\times \frac{1}{100}+\frac{3}{5}\times \frac{1}{50}}

P(B|X)= \frac{\frac{1}{250}}{\frac{1}{250}+\frac{3}{250}}

P(B|X)= \frac{\frac{1}{250}}{\frac{4}{250}}

P(B|X)= \frac{1}{4}

Hence, the probability that defective item was produced by machine B =

P(B|X)= \frac{1}{4} .

Question:9 Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.

Answer:

A: the first groups will win

B: the second groups will win

P(A)=0.6

P(B)=0.4

X: Event of introducing a new product.

Probability of introducing a new product if the first group wins : P(X|A)=0.7

Probability of introducing a new product if the second group wins : P(X|B)=0.3

P(B|X)= \frac{P(B).P(X|B)}{P(B).P(X|B)+P(A).P(X|A)}

p(B|X) = \frac{0.4\times 0.3}{0.4\times 0.3+0.6\times 0.7}

p(B|X) = \frac{0.12}{0.12+0.42}

p(B|X) = \frac{0.12}{0.54}

p(B|X) = \frac{12}{54}

p(B|X) = \frac{2}{9}

Hence, the probability that the new product introduced was by the second group :

p(B|X) = \frac{2}{9}

Question:10 Suppose a girl throws a die. If she gets a 5 or 6 , she tosses a coin three times and notes the number of heads. If she gets 1,2,3 or 4 , she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1,2,3 or 4 with the die?

Answer:

Let, A: Outcome on die is 5 or 6.

B: Outcome on die is 1,2,3,4

P(A)=\frac{2}{6}=\frac{1}{3}

P(B)=\frac{4}{6}=\frac{2}{3}

X: Event of getting exactly one head.

Probability of getting exactly one head when she tosses a coin three times : P(X|A)=\frac{3}{8}

Probability of getting exactly one head when she tosses a coin one time : P(X|B)=\frac{1}{2}

P(B|X)= \frac{P(B).P(X|B)}{P(B).P(X|B)+P(A).P(X|A)}

P(B|X)= \frac{\frac{2}{3}\times \frac{1}{2}}{\frac{2}{3}\times \frac{1}{2}+\frac{1}{3}\times \frac{3}{8}}

P(B|X)= \frac{\frac{1}{3}}{\frac{1}{3}+\frac{1}{8}}

P(B|X)= \frac{\frac{1}{3}}{\frac{11}{24}}

P(B|X)= \frac{1\times 24}{3\times 11}=\frac{8}{11}

Hence, the probability that she threw 1,2,3 or 4 with the die =

P(B|X)=\frac{8}{11}

Question:11 A manufacturer has three machine operators A,B and C. The first operator A produces 1^{o}/_{o} defective items, where as the other two operators B and C produce 5^{o}/_{o} and 7^{o}/_{o} defective items respectively. A is on the job for 50^{o}/_{o} of the time, B is on the job for 30^{o}/_{o} of the time and C is on the job for 20^{o}/_{o} of the time. A defective item is produced, what is the probability that it was produced by A ?

Answer:

Let A: time consumed by machine A =50\%

B: time consumed by machine B =30\%

C: time consumed by machine C =20\%

Total drivers = 12000

P(A)=\frac{50}{100}=\frac{1}{2}

P(B)=\frac{30}{100}=\frac{3}{10}

P(C)=\frac{20}{100}=\frac{1}{5}

D: Event of producing defective items

P(D|A)= \frac{1}{100}

P(D|B)= \frac{5}{100}

P(D|C)= \frac{7}{100}

P(A|D)=\frac{P(A).P(D|A)}{P(B).P(D|B)+P(A).P(D|A)+P(C).P(D|C)}

P(A|D)=\frac{\frac{1}{2}\times \frac{1}{100}}{\frac{1}{2}\times \frac{1}{100}+\frac{3}{10}\times \frac{5}{100}+\frac{1}{5}\times \frac{7}{100}}

P(A|D)=\frac{\frac{1}{2}\times \frac{1}{100}}{\frac{1}{100} (\frac{1}{2}+\frac{3}{2}+\frac{7}{5})}

P(A|D)=\frac{\frac{1}{2}}{ (\frac{17}{5})}

P(A|D)= \frac{5}{34}

Hence, the probability that defective item was produced by A =

P(A|D)= \frac{5}{34}

Question:12 A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.

Answer:

Let A : Event of choosing a diamond card.

B : Event of not choosing a diamond card.

P(A)=\frac{13}{52}=\frac{1}{4}

P(B)=\frac{39}{52}=\frac{3}{4}

X : The lost card.

If lost card is diamond then 12 diamond cards are left out of 51 cards.

Two diamond cards are drawn out of 12 diamond cards in ^{12}\textrm{C}_2 ways.

Similarly, two cards are drawn out of 51 cards in ^{51}\textrm{C}_2 ways.

Probablity of getting two diamond cards when one diamond is lost : P(X|A)= \frac{^{12}\textrm{C}_2}{^{51}\textrm{C}_2}

P(X|A)=\frac{12!}{10!\times 2!}\times \frac{49!\times 2!}{51!}

P(X|A)=\frac{11\times 12}{50\times 51}

P(X|A)=\frac{22}{425}

If lost card is not diamond then 13 diamond cards are left out of 51 cards.

Two diamond cards are drawn out of 13 diamond cards in ^{13}\textrm{C}_2 ways.

Similarly, two cards are drawn out of 51 cards in ^{51}\textrm{C}_2 ways.

Probablity of getting two diamond cards when one diamond is not lost : P(X|B)= \frac{^{13}\textrm{C}_2}{^{51}\textrm{C}_2}

P(X|B)=\frac{13!}{11!\times 2!}\times \frac{49!\times 2!}{51!}

P(X|B)=\frac{13\times 12}{50\times 51}

P(X|B)=\frac{26}{425}

The probability of the lost card being a diamond : P(B|X)

P(B|X)= \frac{P(B).P(X|B)}{P(B).P(X|B)+P(A).P(X|A)}

P(B|X)= \frac{\frac{1}{4}\times \frac{22}{425}}{\frac{1}{4}\times \frac{22}{425}+\frac{3}{4}\times \frac{26}{425}}

P(B|X)= \frac{\frac{11}{2}}{25}

P(B|X)= \frac{11}{50}

Hence, the probability of the lost card being a diamond :

P(B|X)= \frac{11}{50}

Question:13 Probability that A speaks truth is \frac{4}{5} . A coin is tossed. A reports that a head appears. The probability that actually there was head is

(A) \frac{4}{5}

(B) \frac{1}{2}

C) \frac{1}{5}

(D) \frac{2}{5}

Answer:

Let A : A speaks truth

B : A speaks false

P(A)=\frac{4}{5}

P(B)=1-\frac{4}{5}=\frac{1}{5}

X : Event that head appears.

A coin is tossed , outcomes are head or tail.

Probability of getting head whether A speaks thruth or not is \frac{1}{2}

P(X|A)=P(X|B)=\frac{1}{2}

P(A|X)= \frac{P(A).P(X|A)}{P(B).P(X|B)+P(A).P(X|A)}

P(A|X)= \frac{\frac{4}{5}\times \frac{1}{2}}{\frac{4}{5}\times \frac{1}{2}+\frac{1}{5}\times \frac{1}{2}}

P(A|X)= \frac{\frac{4}{5}}{\frac{4}{5}+\frac{1}{5}}

P(A|X)= \frac{\frac{4}{5}}{\frac{1}{1}}

P(A|X)={\frac{4}{5}}

The probability that actually there was head is P(A|X)={\frac{4}{5}}

Hence, option A is correct.

Question:14 If A and B are two events such that A\subset B and P(B)\neq 0, then which of the following is correct?

(A) P(A\mid B)=\frac{P(B)}{P(A)}

(B) P(A\mid B)< P(A)

(C) P(A\mid B)\geq P(A)

(D) None of these

Answer:

If A\subset B and P(B)\neq 0, then

\Rightarrow \, \, \, (A\cap B) = A

Also, P(A)< P(B)

P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(A)}{P(B)}

We know that P(B)\leq 1

1\leq \frac{1}{P(B)}

P(A)\leq \frac{P(A)}{P(B)}

P(A)\leq P(A|B)

Hence, we can see option C is correct.


NCERT solutions for class 12 maths chapter 13 probability-Exercise: 13.4

Question:1(i) State which the following are not the probability distributions of a random variable. Give reasons for your answer.

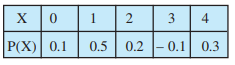
1648016633997

Answer:

As we know the sum of probabilities of a probability distribution is 1.

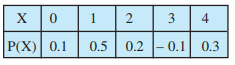
1648016679414

Sum of probabilities =0.4+0.4+0.2=1

\therefore The given table is the probability distributions of a random variable.

Question:1(ii) State which of the following are not the probability distributions of a random variable. Give reasons for your answer.

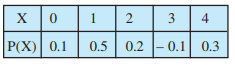
1648016742824

Answer:

As we know probabilities cannot be negative for a probability distribution .

1648016794941

P(3) = -0.1

\therefore The given table is not a the probability distributions of a random variable.

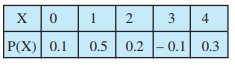
Question:1(iii) State which of the following are not the probability distributions of a random variable. Give reasons for your answer.

1648016848345

Answer:

As we know sum of probabilities of a probability distribution is 1.

1648016877733

Sum of probablities =0.6+0.1+0.2=0.9\neq 1

\therefore The given table is not a the probability distributions of a random variable because sum of probabilities is not 1.

Question:1(iv) State which of the following are not the probability distributions of a random variable. Give reasons for your answer.

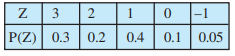
1648016924524

Answer:

As we know sum of probabilities of a probability distribution is 1.

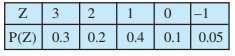
1648016951015

Sum of probablities =0.3+0.2+0.4+0.1+0.05=1.05\neq 1

\therefore The given table is not a the probability distributions of a random variable because sum of probabilities is not 1.

Question:2 An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X? Is X a random variable ?

Answer:

B = black balls

R = red balls

The two balls can be selected as BR,BB,RB,RR.

X = number of black balls.

\therefore X(BB)=2

X(RB)=1

X(BR)=1

X(RR)=0

Hence, possible values of X can be 0, 1 and 2.

Yes, X is a random variable.

Question:3 Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possibl valuess of X ?

Answer:

The difference between the number of heads and the number of tails obtained when a coin is tossed 6 times are :

\therefore X(6H,0T)=\left | 6-0 \right |=6

\Rightarrow \, \, X(5H,1T)=\left | 5-1 \right |=4

\Rightarrow \, \, X(4H,2T)=\left | 4-2 \right |=2

\Rightarrow \, \, X(3H,3T)=\left | 3-3 \right |=0

\Rightarrow \, \, X(2H,4T)=\left | 2-4\right |=2

\Rightarrow \, \, X(1H,5T)=\left | 1-5\right |=4

\Rightarrow \, \, X(0H,6T)=\left |0-6\right |=6

Thus, possible values of X are 0, 2, 4 and 6.

Question:4(i) Find the probability distribution of

number of heads in two tosses of a coin.

Answer:

When coin is tossed twice then sample space =\left \{ HH,HT,TH,TT \right \}

Let X be number of heads.

\therefore X(HH)=2

X(HT)=1

X(TH)=1

X(TT)=0

X can take values of 0,1,2.

P(HH)=P(HT)=P(TH)=P(TT)=\frac{1}{4}

P(X=0)=P(TT)=\frac{1}{4}

P(X=2)=P(HH)=\frac{1}{4}

P(X=1)=P(HT)+P(TH)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}

Table is as shown :

X

0

1

2

P(X)

\frac{1}{4}

\frac{1}{2}

\frac{1}{4}


Question:4(ii) Find the probability distribution of

number of tails in the simultaneous tosses of three coins.

Answer:

When 3 coins are simultaneous tossed then sample space =\left \{ HHH,HHT,TTH,TTT,HTH,THT,THH,HTT \right \}

Let X be number of tails.

\therefore X can be 0,1,2,3

X can take values of 0,1,2.

P(X=0)=P(HHH)=\frac{1}{8}

P(X=1)=P(HHT)+P(HTH)+P(THH)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}

P(X=2)=P(THT)+P(HTT)+P(TTH)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}

P(X=3)=P(TTT)=\frac{1}{8}

Table is as shown :

X

0

1

2

3

P(X)

\frac{1}{8}

\frac{3}{8}

\frac{3}{8}

\frac{1}{8}


Question:4(iii) Find the probability distribution of

number of heads in four tosses of a coin.

Answer:

When coin is tossed 4 times then sample space =\left \{ HHHH,HHHT,TTTH,HTHH,THHT,TTHH,HHTT ,TTTT,HTTH,THTH,HTHT,HTTT,THHH,THTT,HHTH,TTHT\right \}

Let X be number of heads.

\therefore X can be 0,1,2,3,4

P(X=0)=P(TTTT)=\frac{1}{16}

P(X=1)=P(HTTT)+P(TTTH)+P(THTT)=(TTHT)=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{4}{16}=\frac{1}{4}

P(X=2)=P(THHT)+P(HHTT)+P(HTTH)+P(TTHH)+P(HTHT)+P(THTH)=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{6}{16}=\frac{3}{8}

P(X=3)=P(HHHT)+P(THHH)+P(HHTH)+P(HTHH)=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{4}{16}=\frac{1}{4}

P(X=4)=P(HHHH)=\frac{1}{16}

Table is as shown :

X

0

1

2

3

4

P(X)

\frac{1}{16}

\frac{1}{4}

\frac{3}{8}

\frac{1}{4}

\frac{1}{16}


Question:5(i) Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as

number greater than 4

Answer:

When a die is tossed twice , total outcomes = 36

Number less than or equal to 4 in both toss : P(X=0)=\frac{4}{6} \times \frac{4}{6}=\frac{4}{9}

Number less than or equal to 4 in first toss and number more than or equal to 4 in second toss + Number less than or equal to 4 in second toss and number more than or equal to 4 in first toss: P(X=1)=\frac{4}{6} \times \frac{2}{6}+ \frac{2}{6}\times \frac{4}{6}=\frac{4}{9}

Number less than 4 in both tosses : P(X=2)=\frac{2}{6} \times \frac{2}{6}= \frac{1}{9}

Probability distribution is as :

X

0

1

2

P(X)

\frac{4}{9}

\frac{4}{9}

\frac{1}{9}


Question:5(ii) Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as

six appears on at least one die .

Answer:

When a die is tossed twice , total outcomes = 36

Six does not appear on any of the die : P(X=0)=\frac{5}{6} \times \frac{5}{6}=\frac{25}{36}

Six appear on atleast one die : P(X=1)=\frac{1}{6} \times \frac{5}{6}+ \frac{1}{6}\times \frac{5}{6}=\frac{5}{18}

Probability distribution is as :

X

0

1

P(X)

\frac{25}{36}

\frac{5}{18}


Question:6 From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.

Answer:

Total bulbs = 30

defective bulbs = 6

Non defective bulbs =30-6=24

P(defective \, \, \, \, \, bulbs)=\frac{6}{30}=\frac{1}{5}

P(Non \, \, \, \, defective \, \, \, \, \, bulbs)=\frac{24}{30}=\frac{4}{5}

4 bulbs is drawn at random with replacement.

Let X : number of defective bulbs

4 Non defective bulbs and 0 defective bulbs : P(X=0)={4}\textrm{C}_0\frac{4}{5}.\frac{4}{5}.\frac{4}{5}.\frac{4}{5}=\frac{256}{625}

3 Non defective bulbs and 1 defective bulbs : P(X=1)={4}\textrm{C}_1\frac{1}{5}.\frac{4}{5}.\frac{4}{5}.\frac{4}{5}=\frac{256}{625}

2 Non defective bulbs and 2 defective bulbs : P(X=2)={4}\textrm{C}_2\frac{1}{5}.\frac{1}{5}.\frac{4}{5}.\frac{4}{5}=\frac{96}{625}

1 Non defective bulbs and 3 defective bulbs : P(X=3)={4}\textrm{C}_3\frac{1}{5}.\frac{1}{5}.\frac{1}{5}.\frac{4}{5}=\frac{16}{625}

0 Non defective bulbs and 4 defective bulbs : P(X=4)={4}\textrm{C}_4\frac{1}{5}.\frac{1}{5}.\frac{1}{5}.\frac{1}{5}=\frac{1}{625}

the probability distribution of the number of defective bulbs is as :

X

0

1

2

3

4

P(X)

\frac{256}{625}

\frac{256}{625}

\frac{96}{625}

\frac{16}{625}

\frac{1}{625}


Question:7 A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.

Answer:

the coin is tossed twice, total outcomes =4 =\left \{ HH,TT,HT,TH \right \}

probability of getting a tail be x.

i.e. P(T)=x

Then P(H)=3x

P(T)+P(H)=x+3x=1

4x=1

x=\frac{1}{4}

P(T)=\frac{1}{4} and P(H)=\frac{3}{4}

Let X : number of tails

No tail : P(X=0)=P(H).P(H)=\frac{3}{4}\times \frac{3}{4}=\frac{9}{16}

1 tail : P(X=1)=P(HT)+P(TH)=\frac{3}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{3}{4}=\frac{3}{8}

2 tail : P(X=2)=P(TT)=\frac{1}{4}\times \frac{1}{4}=\frac{1}{16}

the probability distribution of number of tails are

X

0

1

2

P(X)

\frac{9}{16}

\frac{3}{8}

\frac{1}{16}


Question:8(i) A random variable X has the following probability distribution:

1648017017487

k

Answer:

1648017033239

Sum of probabilities of probability distribution of random variable is 1.

\therefore \, \, \, \, 0+k+2k+2k+3k+k^{2}+2k^{2}+7k^{2}+k=1

10k^{2}+9k-1=0

(10k-1)(k+1)=0

k=\frac{1}{10}\, \, and\, \, k=-1

Question:8(ii) A random variable X has the following probability distribution:

1648017090278

P(X< 3)

Answer:

P(X< 3)=P(X=0)+P(X=1)+P(X=2)

=0+K+2K

=3K

=3\times \frac{1}{10}

= \frac{3}{10}

Question:8(iii) A random variable X has the following probability distribution:

1648017138534

P(X> 6)

Answer:

P(X> 6)=P(X=7)

=7K^2+K

=7\times (\frac{1}{10})^2+\frac{1}{10}

=\frac{7}{100}+\frac{1}{10}

=\frac{17}{100}

Question:8(iv) A random variable X has the following probability distribution:

P(0< X< 3)

Answer:

1648017209970P(0< X< 3)=P(X=1)+P(X=2)

=k+2k

=3k

=3\times \frac{1}{10}

= \frac{3}{10}

Question:9(a) The random variable X has a probability distribution P(X) of the following form, where k is some number :

P(X)=\left\{\begin{matrix} k, if&i x=0\\ 2k, if& x=1\\ 3k, if& x=2\\ 0,& otherwise \end{matrix}\right.

Determine the value of k.

Answer:

Sum of probabilities of probability distribution of random variable is 1.


\therefore \, \, \, \, k+2k+3k+0=1

6k=1

k=\frac{1}{6}

Question:9(b) The random variable X has a probability distribution P(X) of the following form, where k is some number :

P(X)=\left\{\begin{matrix} k,& if & x=0\\ 2k,& if& x=1\\ 3k,& if& x=2\\ 0,& otherwise& \end{matrix}\right.

Find P\left ( X< 2 \right ),P\left ( X\leq 2 \right ),P\left ( X\geq 2 \right ).

Answer:

P(X< 2)=P(X=0)+P(X=1)

=k+2k

=3k

=3\times \frac{1}{6}

= \frac{1}{2}

P(X\leq 2)=P(X=0)+P(X=1)+p(X=2)

=k+2k+3k

=6k

=6\times \frac{1}{6}

=1

P(X\geq 2)=P(X=2)+P(X> 2)

=3k+0

=3\times \frac{1}{6}=\frac{1}{2}

Question:10 Find the mean number of heads in three tosses of a fair coin.

Answer:

Let X be the success of getting head.

When 3 coins are tossed then sample space =\left \{ HHH,HHT,TTH,TTT,HTH,THT,THH,HTT \right \}

\therefore X can be 0,1,2,3

P(X=0)=P(TTT)=\frac{1}{8}

P(X=1)=P(HTT)+P(TTH)+P(HTH)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}

P(X=2)=P(HHT)+P(HTH)+P(THH)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}

P(X=3)=P(HHH)=\frac{1}{8}

The probability distribution is as

X

0

1

2

3

P(X)

\frac{1}{8}

\frac{3}{8}

\frac{3}{8}

\frac{1}{8}

mean number of heads :

=0\times \frac{1}{8}+1\times \frac{3}{8}+2\times \frac{3}{8}+3\times \frac{1}{8}

= \frac{3}{8}+ \frac{6}{8}+ \frac{3}{8}

=\frac{12}{8}

=\frac{3}{2}=1.5

Question:11 Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X .

Answer:

X denotes the number of sixes, when two dice are thrown simultaneously.

X can be 0,1,2.

\therefore Not getting six on dice P(X)=\frac{25}{36}

Getting six on one time when thrown twice : P(X=1)=2\times \frac{5}{6}\times \frac{1}{6}=\frac{10}{36}

Getting six on both dice : P(X=2)= \frac{1}{36}=\frac{1}{36}

X

0

1

2

P(X)

\frac{25}{36}

\frac{10}{36}

\frac{1}{36}

Expectation of X = E(X)

E(X)=0\times \frac{25}{36}+1\times \frac{10}{36}+2\times \frac{1}{36}

E(X)= \frac{12}{36}

E(X)= \frac{1}{3}

Question:12 Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find E(X).

Answer:

Two numbers are selected at random (without replacement) from the first six positive integers in 6\times 5=30 ways.

X denote the larger of the two numbers obtained.

X can be 2,3,4,5,6.

X=2, obsevations : (1,2),(2,1)

P(X=2)=\frac{2}{30}=\frac{1}{15}

X=3, obsevations : (1,3),(3,1),(2,3),(3,2)

P(X=3)=\frac{4}{30}=\frac{2}{15}

X=4, obsevations : (1,4),(4,1),(2,4),(4,2),(3,4),(4,3)

P(X=4)=\frac{6}{30}=\frac{3}{15}

X=5, obsevations : (1,5),(5,1),(2,5),(5,2),(3,5),(5,3),(4,5),(5,4)

P(X=5)=\frac{8}{30}=\frac{4}{15}

X=6, obsevations : (1,6),(6,1),(2,6),(6,2),(3,6),(6,3),(4,6),(6,4),(5,6),(6,5)

P(X=6)=\frac{10}{30}=\frac{1}{3}

Probability distribution is as follows:

X

2

3

4

5

6

P(X)

\frac{1}{15}

\frac{2}{15}

\frac{3}{15}

\frac{4}{15}

\frac{1}{3}


E(X)=2\times \frac{1}{15}+3\times \frac{2}{15}+4\times \frac{3}{15}+5\times \frac{4}{15}+6\times \frac{1}{3}

E(X)= \frac{2}{15}+ \frac{2}{5}+ \frac{4}{5}+ \frac{4}{3}+ \frac{2}{1}

E(X)= \frac{70}{15}

E(X)= \frac{14}{3}

Question:13 Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X .

Answer:

X denote the sum of the numbers obtained when two fair dice are rolled.

Total observations = 36

X can be 2,3,4,5,6,7,8,9,10,11,12

P(X=2)=P(1,1)=\frac{1}{36}

P(X=3)=P(1,2)+P(2,1)=\frac{2}{36}=\frac{1}{18}

P(X=4)=P(1,3)+P(3,1)+P(2,2)=\frac{3}{36}=\frac{1}{12}

P(X=5)=P(1,4)+P(4,1)+P(2,3)+P(3,2)=\frac{4}{36}=\frac{1}{9}

P(X=6)=P(1,5)+P(5,1)+P(2,4)+P(4,2)+P(3,3)=\frac{5}{36}

P(X=7)=P(1,6)+P(6,1)+P(2,5)+P(5,2)+P(3,4)+P(4,3)=\frac{6}{36}=\frac{1}{6}

P(X=8)=P(2,6)+P(6,2)+P(3,5)+P(5,3)+P(4,4)=\frac{5}{36} P(X=9)=P(3,6)+P(6,3)+P(4,5)+P(5,4)=\frac{4}{36}=\frac{1}{9}

P(X=10)=P(4,6)+P(6,4)+P(5,5)=\frac{3}{36}=\frac{1}{12}

P(X=11)=P(5,6)+P(6,5)=\frac{2}{36}=\frac{1}{18}

P(X=12)=P(6,6)=\frac{1}{36}

Probability distribution is as follows :

X

2

3

4

5

6

7

8

9

10

11

12

P(X)

\frac{1}{36}

\frac{1}{18}

\frac{1}{12}

\frac{1}{9}

\frac{5}{36}

\frac{1}{6}

\frac{5}{36}

\frac{1}{9}

\frac{1}{12}

\frac{1}{18}

\frac{1}{36}

E(X)=2\times \frac{1}{36}+3\times \frac{1}{18}+4\times \frac{1}{12}+5\times \frac{1}{9}+6\times \frac{5}{36}+7\times \frac{1}{6}+8\times \frac{5}{36}+9\times \frac{1}{9}+10\times \frac{1}{12}+11\times \frac{1}{18}+12\times \frac{1}{36}

E(X)=\frac{1}{18}+\frac{1}{6}+\frac{1}{3}+\frac{5}{9}+\frac{5}{6}+\frac{7}{6}+\frac{10}{9}+1+\frac{5}{6}+\frac{11}{18}+\frac{1}{3}

E(X)=7

E(X^2)=4\times \frac{1}{36}+9\times \frac{1}{18}+16\times \frac{1}{12}+25\times \frac{1}{9}+36\times \frac{5}{36}+49\times \frac{1}{6}+64\times \frac{5}{36}+81\times \frac{1}{9}+100\times \frac{1}{12}+121\times \frac{1}{18}+144\times \frac{1}{36}

E(X^2)=\frac{987}{18}=\frac{329}{6}=54.833

Variance = E(X^2)-(E(X))^2

=54.833-7^2

=54.833-49

=5.833

Standard deviation = =\sqrt{5.833}=2.415

Question:14 A class has 15 students whose ages are 14,17,15,14,21,17,19,20,16,18,20,17,16,19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable X? Find mean, variance and standard deviation of X .

Answer:

Total students = 15

probability of selecting a student :

=\frac{1}{15}

The information given can be represented as frequency table :

X

14

15

16

17

18

19

20

21

f

2

1

2

3

1

2

3

1

P(X=14)=\frac{2}{15} P(X=15)=\frac{1}{15} P(X=16)=\frac{2}{15}

P(X=17)=\frac{3}{15}=\frac{1}{5} P(X=18)=\frac{1}{15} P(X=19)=\frac{2}{15}

P(X=20)=\frac{3}{15}=\frac{1}{5} P(X=21)=\frac{1}{15}

Probability distribution is as :

X

14

15

16

17

18

19

20

21

P(X)

\frac{2}{15}

\frac{1}{15}

\frac{2}{15}

\frac{1}{5}

\frac{1}{15}

\frac{2}{15}

\frac{1}{5}

\frac{1}{15}

E(X)=14\times \frac{2}{15}+15\times \frac{1}{15}+16\times \frac{2}{15}+17\times \frac{1}{5}+18\times \frac{1}{15}+19\times \frac{2}{15}+20\times \frac{1}{5}+21\times \frac{1}{15}

E(X)=\frac{263}{15}=17.53

E(X^2)=14^2\times \frac{2}{15}+15^2\times \frac{1}{15}+16^2\times \frac{2}{15}+17^2\times \frac{1}{5}+18^2\times \frac{1}{15}+19^2\times \frac{2}{15}+20^2\times \frac{1}{5}+21^2\times \frac{1}{15}

E(X^2)=\frac{4683}{15}=312.2

Variance =E(X^2)-(E(X))^2

Variance =312.2-(17.53)^2

Variance =312.2-307.42

Variance =4.78

Standard\, \, deviation =\sqrt{4.78}=2.19

Question:15 In a meeting, 70^{o}/_{o} of the members favour and 30^{o}/_{o} oppose a certain proposal. A member is selected at random and we take X=0 . if he opposed, and X=1 if he is in favour. Find E(X) and Var (X) .

Answer:

Given :

P(X=0)=30\%=\frac{30}{100}=0.3

P(X=1)=70\%=\frac{70}{100}=0.7

Probability distribution is as :

X

0

1

P(X)

0.3

0.7

E(X)=0\times 0.3+1\times 0.7

E(X)= 0.7

E(X^2)=0^2\times 0.3+1^2\times 0.7

E(X^2)= 0.7

Variance = E(X^2)-(E(X))^2

Variance = 0.7-(0.7)^2

Variance = 0.7-0.49=0.21

Question:16 The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is, Choose the correct answer in the following:

(A) 1

(B) 2

(C) 5

(D) \frac{8}{3}

Answer:

X is number representing on die.

Total observations = 6

P(X=1)=\frac{3}{6}=\frac{1}{2}

P(X=2)=\frac{2}{6}=\frac{1}{3}

P(X=5)=\frac{1}{6}

X

1

2

5

P(X)

\frac{1}{2}

\frac{1}{3}

\frac{1}{6}

E(X)=1\times \frac{1}{2}+2\times \frac{1}{3}+5\times \frac{1}{6}

E(X)= \frac{1}{2}+ \frac{2}{3}+ \frac{5}{6}

E(X)=\frac{12}{6}=2

Option B is correct.

Question:17 Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is Choose the correct answer in the following:

(A) \frac{37}{221}

(B) \frac{5}{13}

(C) \frac{1}{13}

(D) \frac{2}{13}

Answer:

X be number od aces obtained.

X can be 0,1,2

There 52 cards and 4 aces, 48 are non-ace cards.

P(X=0)=P(0 \, ace\, and\, 2\, non\, ace\, cards)=\frac{^4C_2.^4^8C_2}{^5^2C_2}=\frac{1128}{1326}

P(X=1)=P(1 \, ace\, and\, 1\, non\, ace\, cards)=\frac{^4C_1.^4^8C_1}{^5^2C_2}=\frac{192}{1326}

P(X=2)=P(2 \, ace\, and\, 0\, non\, ace\, cards)=\frac{^4C_2.^4^8C_0}{^5^2C_2}=\frac{6}{1326}

The probability distribution is as :

X

0

1

2

P(X)

\frac{1128}{1326}

\frac{192}{1326}

\frac{6}{1326}


E(X)=0\times \frac{1128}{1326}+1\times \frac{192}{1326}+2\times \frac{6}{1326}

E(X)=\frac{204}{1326}

E(X)=\frac{2}{13}

Option D is correct.


NCERT solutions for class 12 maths chapter 13 probability-Exercise: 13.5

Question:1(i) A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of

5 successes?

Answer:

X be the number of success of getting an odd number.

P(probability\, of\, getting\, odd\, number)=\frac{3}{6}=\frac{1}{2}

\therefore \, \, \, \, q=1-P=1-\frac{1}{2}=\frac{1}{2}

X has a binomial distribution.

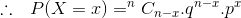
\therefore \, \, \, \, P(X=x)=^nC_n_-_x.q^{n-x}.p^x

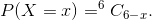
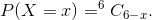
P(X=x)=^6C_6_-_x. (\frac{1}{2})^{6-x} . (\frac{1}{2})^{x}

P(X=x)=^6C_6_-_x. (\frac{1}{2})^{6}

P(5\, \, \, success) =P(x=5)

= ^6C_5 .(\frac{1}{2})^6

= 6 .(\frac{1}{64})

= \frac{3}{32}

Question:1(ii) A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of

at least 5 successes?

Answer:

X be a number of success of getting an odd number.

P(probability\, of\, getting\, odd\, number)=\frac{3}{6}=\frac{1}{2}

\therefore \, \, \, \, q=1-P=1-\frac{1}{2}=\frac{1}{2}

X has a binomial distribution.

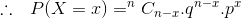
\therefore \, \, \, \, P(X=x)=^nC_n_-_x.q^{n-x}.p^x

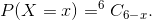
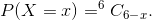
P(X=x)=^6C_6_-_x. (\frac{1}{2})^{6-x} . (\frac{1}{2})^{x}

P(X=x)=^6C_6_-_x. (\frac{1}{2})^{6}

P(At \, \, least \, \, 5\, \, \, success) =P(x\geq 5)

=P(X=5)+P(X=6)

= ^6C_5 .(\frac{1}{2})^6+^6C_6 .(\frac{1}{2})^6

= 6 .(\frac{1}{64}) + (\frac{1}{64})

= \frac{7}{64}

Question:1(iii) A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of

at most 5 successes?

Answer:

X be a number of success of getting an odd number.

P(probability\, of\, getting\, odd\, number)=\frac{3}{6}=\frac{1}{2}

\therefore \, \, \, \, q=1-P=1-\frac{1}{2}=\frac{1}{2}

X has a binomial distribution.

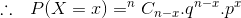
\therefore \, \, \, \, P(X=x)=^nC_n_-_x.q^{n-x}.p^x

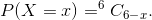
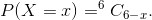
P(X=x)=^6C_6_-_x. (\frac{1}{2})^{6-x} . (\frac{1}{2})^{x}

P(X=x)=^6C_6_-_x.(\frac{1}{2})^{6}

P(atmost\, \, 5\, \, \, success) =P(x\leq 5)

=1-P(X> 5)

=1-P(X= 5)

= 1-^6C_6 .(\frac{1}{2})^6

= 1- (\frac{1}{64})

= \frac{63}{64}

Question:2 A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes

Answer:

A pair of dice is thrown 4 times.X be getting a doublet.

Probability of getting doublet in a throw of pair of dice :

P=\frac{6}{36}=\frac{1}{6}

q=1-P=1-\frac{1}{6}=\frac{5}{6}

X has a binomial distribution,n=4

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^4C_x. (\frac{5}{6})^{4-x} . (\frac{1}{6})^{x}

P(X=x)=^4C_x. \frac{5^{4-x}}{6^4}

Put x = 2

P(X=2)=^4C_2. \frac{5^{4-2}}{6^4}

P(X=2)=6\times \frac{25}{1296}

P(X=2)= \frac{25}{216}

Question:3 There are 5^{o}/_{o} defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?

Answer:

There are 5^{o}/_{o} defective items in a large bulk of items.

X denotes the number of defective items in a sample of 10.

\Rightarrow \, \, P=\frac{5}{100}=\frac{1}{2}

\Rightarrow \, \, q=1-\frac{1}{20}=\frac{19}{20}

X has a binomial distribution, n=10.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^1^0C_x. (\frac{19}{20})^{10-x} . (\frac{1}{20})^{x}

P(not\, more\, than\, one\, defective item)=p(X\leq 1)

=P(X=0)+P(X=1)

=^{10}C_0(\frac{19}{20})^{10} . (\frac{1}{20})^{0}+^{10}C_1(\frac{19}{20})^{9} . (\frac{1}{20})^{1}

=(\frac{19}{20})^{9} . (\frac{29}{20})^{1}

Question:4(i) Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that

all the five cards are spades?

Answer:

Let X represent a number of spade cards among five drawn cards. Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards.

We have 13 spades.

P=\frac{13}{52}=\frac{1}{4}

q=1-P=1-\frac{1}{4}=\frac{3}{4}

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{3}{4})^{5-x} . (\frac{1}{4})^{x}

Put X=5 ,

P(X=5)=^5C_5. (\frac{3}{4})^{0} . (\frac{1}{4})^{5}

=1\times \frac{1}{1024}

= \frac{1}{1024}

Question:4(ii) Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that

only 3 cards are spades?

Answer:

Let X represent a number of spade cards among five drawn cards. Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards.

We have 13 spades.

P=\frac{13}{52}=\frac{1}{4}

q=1-P=1-\frac{1}{4}=\frac{3}{4}

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{3}{4})^{5-x} . (\frac{1}{4})^{x}

Put X=3 ,

P(X=3)=^5C_3. (\frac{3}{4})^{2} . (\frac{1}{4})^{3}

=10\times \frac{9}{16}\times \frac{1}{64}

=\frac{45}{512}

Question:4(iii) Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that

none is a spade?

Answer:

Let X represent number of spade cards among five drawn cards. Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards.

We have 13 spades .

P=\frac{13}{52}=\frac{1}{4}

q=1-P=1-\frac{1}{4}=\frac{3}{4}

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{3}{4})^{5-x} . (\frac{1}{4})^{x}

Put X=0 ,

P(X=0)=^5C_0. (\frac{3}{4})^{5} . (\frac{1}{4})^{0}

=1\times \frac{243}{1024}

= \frac{243}{1024}

Question:5(i) The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. . Find the probability that out of 5 such bulbs

none will fuse after 150 days of use.

Answer:

Let X represent number of bulb that will fuse after 150 days of use .Trials =5

P=0.005

q=1-0.005=1-0.005=0.95

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (0.95)^{5-x} . (0.05)^{x}

Put X=0 ,

P(X=0)=^5C_0. (0.95)^{5} . (0.05)^{0}

=(0.95)^{5}

Question:5(ii) The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs

not more than one will fuse after 150 days of use.

Answer:

Let X represent a number of the bulb that will fuse after 150 days of use. Trials =5

P=0.005

q=1-0.005=1-0.005=0.95

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (0.95)^{5-x} . (0.05)^{x}

Put X\leq 1 ,

P(X\leq 1)=P(X=0)+P(X=1)

=^5C_0. (0.95)^{5} . (0.05)^{0}+^5C_1 (0.95)^{4} . (0.05)^{1}

=(0.95)^{5}+ (0.25)(0.95)^4

=(0.95)^{4}(0.95+ 0.25)

=(0.95)^{4}\times 1.2

Question:5(iii) The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs

more than one will fuse after 150 days of use.

Answer:

Let X represent number of bulb that will fuse after 150 days of use .Trials =5

P=0.005

q=1-0.005=1-0.005=0.95

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (0.95)^{5-x} . (0.05)^{x}

Put X> 1 ,

P(X> 1)=1-(P(X=0)+P(X=1))

=1-(^5C_0. (0.95)^{5} . (0.05)^{0}+^5C_1 (0.95)^{4} . (0.05)^{1})

=1-((0.95)^{5}+ (0.25)(0.95)^4)

=1-((0.95)^{4}(0.95+ 0.25))

=1-(0.95)^{4}\times 1.2

Question:5(iv) The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05 . Find the probability that out of 5 such bulbs

at least one will fuse after 150 days of use.

Answer:

Let X represent number of bulb that will fuse after 150 days of use .Trials =5

P=0.005

q=1-0.005=1-0.005=0.95

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (0.95)^{5-x} . (0.05)^{x}

Put X\geq 1 ,

P(X\geq 1)=1-P(X< 1)

P(X\geq 1)=1-P(X=0)

=1-^5C_0. (0.95)^{5} . (0.05)^{0}

=1-(0.95)^{5}

Question:6 A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0 ?

Answer:

Let X denote a number of balls marked with digit 0 among 4 balls drawn.

Balls are drawn with replacement.

X has a binomial distribution,n=4.

P=\frac{1}{10}

q=1-P=1-\frac{1}{10}=\frac{9}{10}

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^4C_x. (\frac{9}{10})^{4-x} . (\frac{1}{10})^{x}

Put X = 0,

P(X=0)=^4C_0. (\frac{9}{10})^{4} . (\frac{1}{10})^{0}

= 1.(\frac{9}{10})^{4}

= (\frac{9}{10})^4

Question:7 In an examination, 20 questions of true-false type are asked. Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answers 'true'; if it falls tails, he answers 'false'. Find the probability that he answers at least 12 questions correctly.

Answer:

Let X represent the number of correctly answered questions out of 20 questions.

The coin falls heads, he answers 'true'; if it falls tails, he answers 'false'.

P=\frac{1}{2}

q=1-P=1-\frac{1}{2}=\frac{1}{2}

X has a binomial distribution,n=20

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^2^0C_x. (\frac{1}{2})^{20-x} . (\frac{1}{2})^{x}

P(X=x)=^2^0C_x. (\frac{1}{2})^{20}

P(at\, \, least\, 12\, \,questions \, \, answered\, \, correctly)=P(X\geq 12)

=P(X=12)+P(X=13)..................+P(X=20)

=^{20}C_1_2 (\frac{1}{2})^{20}+^{20}C_1_3(\frac{1}{2})^{20}+..........^{20}C_2_0 (\frac{1}{2})^{20}

=(\frac{1}{2})^{20}(^{20}C_1_2 +^{20}C_1_3+..........^{20}C_2_0 )

Question:8 Suppose X has a binomial distribution B\left [ 6,\frac{1}{2} \right ]. Show that X=3 is the most likely outcome.

(Hint : P(X=3) is the maximum among all of P(x_{i}) , x_{i}=0,1,2,3,4,5,6 )

Answer:

X is a random variable whose binomial distribution is B\left [ 6,\frac{1}{2} \right ].

Here , n=6 and P=\frac{1}{2} .

\therefore \, \,q=1-P= 1-\frac{1}{2}= \frac{1}{2}

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

=^{6}C_x .(\frac{1}{2})^{6-x}(\frac{1}{2})^x

=^{6}C_x (\frac{1}{2})^6

P(X=x) is maximum if ^{6}C_x is maximum.

^{6}C_0 =^{6}C_6 =\frac{6!}{0!.6!}=1

^{6}C_1 =^{6}C_5 =\frac{6!}{1!.5!}=6

^{6}C_2 =^{6}C_4 =\frac{6!}{2!.4!}=15

^{6}C_3 =\frac{6!}{3!.3!}=20

^{6}C_3 is maximum so for x=3 , P(X=3) is maximum.

Question:9 On a multiple choice examination with three possible answers for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing ?

Answer:

Let X represent number of correct answers by guessing in set of 5 multiple choice questions.

Probability of getting a correct answer :

P=\frac{1}{3}

\therefore q=1-P=1-\frac{1}{3}=\frac{2}{3}

X has a binomial distribution,n=5.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{2}{3})^{5-x} . (\frac{1}{3})^{x}

P(guessing \, \, more\, \, than \, 4\, correct\, answer)=P(X\geq 1)

=P(X=4)+P(X=5)

=^5C_4. (\frac{2}{3})^{1} . (\frac{1}{3})^{4}+^5C_5(\frac{2}{3})^{0} . (\frac{1}{3})^{5}

=\frac{10}{243}+\frac{1}{243}

=\frac{11}{243}

Question:10(a) A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \frac{1}{100}. What is the probability that he will win a prize

at least once

Answer:

Let X represent number of winning prizes in 50 lotteries .

P=\frac{1}{100}

q=1-P=1-\frac{1}{100}=\frac{99}{100}

X has a binomial distribution,n=50.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^50C_x. (\frac{1}{100})^{50-x} . (\frac{99}{100})^{x}

P(winning \:at\: least\: once)=P(X\geq 1)

=1-P(X< 1)

=1-P(X= 0)

=1- ^{50}C_0 (\frac{99}{100})^{50}

=1- 1. (\frac{99}{100})^{50}

=1- (\frac{99}{100})^{50}

Question:10(b) A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \frac{1}{100} . What is the probability that he will win a prize

exactly once

Answer:

Let X represent number of winning prizes in 50 lotteries .

P=\frac{1}{100}

q=1-P=1-\frac{1}{100}=\frac{99}{100}

X has a binomial distribution,n=50.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^50C_x. (\frac{1}{100})^{50-x} . (\frac{99}{100})^{x}

P(winning\, exactly\, once)=P(X= 1)

=^{50}C_1 (\frac{99}{100})^{49}.\frac{1}{100}

= 50.(\frac{99}{100})^{49}\frac{1}{100}

=\frac{1}{2} (\frac{99}{100})^{50}

Question:10(c) A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \frac{1}{100} . What is the probability that he will win a prize

at least twice?

Answer:

Let X represent number of winning prizes in 50 lotteries.

P=\frac{1}{100}

q=1-P=1-\frac{1}{100}=\frac{99}{100}

X has a binomial distribution,n=50.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^50C_x. (\frac{1}{100})^{50-x} . (\frac{99}{100})^{x}

P(winning \, \, at \, \, least \, \, twice)=P(X\geq 2)

=1-P(X< 2)

=1-P(X\leq 1)

=1-(P(X=0)+P(X=1))

=1- (\frac{99}{100})^{50}-\frac{1}{2}(\frac{99}{100})^{49}

=1- (\frac{99}{100})^{49}(\frac{1}{2}+\frac{99}{100})

=1- (\frac{99}{100})^{49}\frac{149}{100}

Question:11 Find the probability of getting 5 exactly twice in 7 throws of a die.

Answer:

Let X represent number of times getting 5 in 7 throws of a die.

Probability of getting 5 in single throw of die=P

P=\frac{1}{6}

q=1-P=1-\frac{1}{6}=\frac{5}{6}

X has a binomial distribution,n=7

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^7C_x. (\frac{5}{6})^{7-x} . (\frac{1}{6})^{x}

P(getting\, \, exactly\, \, twice)=P(X= 2)

=^{7}C_2 (\frac{5}{6})^{5}\frac{1}{6}^2

=21 (\frac{5}{6})^{5}\frac{1}{36}

= (\frac{5}{6})^{5}\frac{7}{12}

Question:12 Find the probability of throwing at most 2 sixes in 6 throws of a single die.

Answer:

Let X represent number of times getting 2 six in 6 throws of a die.

Probability of getting 6 in single throw of die=P

P=\frac{1}{6}

q=1-P=1-\frac{1}{6}=\frac{5}{6}

X has a binomial distribution,n=6

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^6C_x. (\frac{5}{6})^{6-x} . (\frac{1}{6})^{x}

P(getting\, \, atmost\, \, two\, six)=P(X\leq 2)

=P(X=0)+P(X=1)+P(X=2)

=^{6}C_0 (\frac{5}{6})^{6}\frac{1}{6}^0+^{6}C_1 (\frac{5}{6})^{5}\frac{1}{6}^1+^{6}C_2 (\frac{5}{6})^{4}\frac{1}{6}^2

=1.(\frac{5}{6})^{6}+6. (\frac{5}{6})^{5}\frac{1}{6}+15 (\frac{5}{6})^{4}\frac{1}{36}

=(\frac{5}{6})^{6}+ (\frac{5}{6})^{5}+ (\frac{5}{6})^{4}\frac{5}{12}

=(\frac{5}{6})^{4}( \frac{5}{6}^{2}+ \frac{5}{6}+\frac{5}{12})

=(\frac{5}{6})^{4}( \frac{25}{36}+ \frac{5}{6}+\frac{5}{12})

=(\frac{5}{6})^{4}( \frac{70}{36})

=(\frac{5}{6})^{4}( \frac{35}{18})

Question:13 It is known that 10^{o}/_{o} of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective?

Answer:

Let X represent a number of times selecting defective items out of 12 articles.

Probability of getting a defective item =P

P=10\%=\frac{10}{100}=\frac{1}{10}

q=1-P=1-\frac{1}{10}=\frac{9}{10}

X has a binomial distribution,n=12

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^1^2C_x. (\frac{9}{10})^{12-x} . (\frac{1}{10})^{x}

P(selectting\, \, 9\,defective \, items)=

=^{12}C_9 (\frac{9}{10})^{3}\frac{1}{10}^9

=220 (\frac{9^3}{10^3})\frac{1}{10^9}

=22 \times \frac{9^3}{10^1^1}

Question:14 In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is

(A) 10^{-1}

(B) \left ( \frac{1}{5} \right )^{5}

(C) \left ( \frac{9}{10} \right )^{5}

(D) \frac{9}{10}

Answer:

Let X represent a number of defective bulbs out of 5 bulbs.

Probability of getting a defective bulb =P

P=\frac{10}{100}=\frac{1}{10}

q=1-P=1-\frac{1}{10}=\frac{9}{10}

X has a binomial distribution,n=5

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{9}{10})^{5-x} . (\frac{1}{10})^{x}

P(non\,of \,bulb\,is\, defective \,)=P(X=0)

=^{5}C_0 (\frac{9}{10})^{5}\frac{1}{10}^0

=1.\frac{9}{10}^5

=(\frac{9}{10})^5

The correct answer is C.

Question:15 The probability that a student is not a swimmer is \frac{1}{5}. Then the probability that out of five students, four are swimmers is

In the following, choose the correct answer:

(A) ^{5}C_{4}\left ( \frac{4}{5} \right )^{4}\frac{1}{5}

(B) \left ( \frac{4}{5} \right )^{4}\frac{1}{5}

(C) ^{5}C_{1}\frac{1}{5}\left ( \frac{4}{5} \right )^{4}

(D) None of these

Answer:

Let X represent number students out of 5 who are swimmers.

Probability of student who are not swimmers =q

q=\frac{1}{5}

P=1-q=1-\frac{1}{5}=\frac{4}{5}

X has a binomial distribution,n=5

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X=x)=^5C_x. (\frac{1}{5})^{5-x} . (\frac{4}{5})^{x}

P(4\, \,students\, \, are\, swimmers)=P(X= 4)

=^5C_4(\frac{1}{5})^{1} . (\frac{4}{5})^{4}

Option A is correct.


NCERT solutions for class 12 maths chapter 13 probability-Miscellaneous Exercise

Question:1(i) A and B are two events such that P(A)\neq 0. Find P(B\mid A), if

A is a subset of B

Answer:

A and B are two events such that P(A)\neq 0.

A\subset B

\Rightarrow \, \, \, \, A\cap B=A

P(A\cap B)=P(B\cap A)=P(A)

P(B|A)=\frac{P(B\cap A)}{P(A)}

P(B|A)=\frac{P( A)}{P(A)}

P(B|A)=1

Question:1(ii) A and B are two events such that P(A)\neq 0. Find P(B\mid A), if

A\cap B=\phi

Answer:

A and B are two events such that P(A)\neq 0.

P(A\cap B)=P(B\cap A)=0

P(B|A)=\frac{P(B\cap A)}{P(A)}

P(B|A)=\frac{0}{P(A)}

P(B|A)=0

Question:2(i) A couple has two children,

Find the probability that both children are males, if it is known that at least one of the children is male.

Answer:

A couple has two children,

sample space =\left \{ (b,b),(g,g),(b,g),(g,b) \right \}

Let A be both children are males and B is at least one of the children is male.

(A\cap B)=\left \{ (b,b) \right \}

P(A\cap B)=\frac{1}{4}

P(A)=\frac{1}{4}

P(B)=\frac{3}{4}

P(A|B)=\frac{P(A\cap B)}{P(B)}

P(A|B)=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}

Question:2(ii) A couple has two children,

Find the probability that both children are females, if it is known that the elder child is a female.

Answer:

A couple has two children,

sample space =\left \{ (b,b),(g,g),(b,g),(g,b) \right \}

Let A be both children are females and B be the elder child is a female.

(A\cap B)=\left \{ (g,g) \right \}

P(A\cap B)=\frac{1}{4}

P(A)=\frac{1}{4}

P(B)=\frac{2}{4}

P(A|B)=\frac{P(A\cap B)}{P(B)}

P(A|B)=\frac{\frac{1}{4}}{\frac{2}{4}}=\frac{1}{2}

Question:3 Suppose that 5^{o}/_{o} of men and 0.25^{o}/_{o} of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.

Answer:

We have 5^{o}/_{o} of men and 0.25^{o}/_{o} of women have grey hair.

Percentage of people with grey hairs =(5+0.25)\%=5.25\%

The probability that the selected haired person is male :

=\frac{5}{5.25}=\frac{20}{21}

Question:4 Suppose that 90^{o}/_{o} of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

Answer:

90^{o}/_{o} of people are right-handed.

P(right-handed)=\frac{9}{10}

P(left-handed)=q=1-\frac{9}{10}=\frac{1}{10}

at most 6 of a random sample of 10 people are right-handed.

the probability that more than 6 of a random sample of 10 people are right-handed is given by,

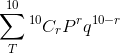
\sum_{T}^{10} ^{10}C_r P^{r} q^{10-r}

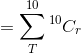
=\sum_{T}^{10} ^{10}C_r \frac{9}{10}^r .(\frac{1}{10})^{10-r}

the probability that at most 6 of a random sample of 10 people are right-handed is given by

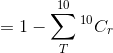=1-\sum_{T}^{10} ^{10}C_r . \frac{9}{10}^r .(\frac{1}{10})^{10-r}

Question:5(i) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y' A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

all will bear 'X' mark.

Answer:

Total balls in urn = 25

Balls bearing mark 'X' =10

Balls bearing mark 'Y' =15

P(ball\, \, bearing\, mark\, 'X')=\frac{10}{25}=\frac{2}{5}

P(ball\, \, bearing\, mark\, 'Y')=\frac{15}{25}=\frac{3}{5}

6 balls are drawn with replacement.

Let Z be a random variable that represents a number of balls with Y mark on them in the trial.

Z has a binomial distribution with n=6.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(Z=0)=^6C_0 (\frac{2}{5})^{6} \frac{3}{5}^0

P(Z=0)=^6C_0 (\frac{2}{5})^{6}

Question:5(ii) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

not more than 2 will bear 'Y' mark.

Answer:

Total balls in urn = 25

Balls bearing mark 'X' =10

Balls bearing mark 'Y' =15

P(ball\, \, bearing\, mark\, 'X')=\frac{10}{25}=\frac{2}{5}

P(ball\, \, bearing\, mark\, 'Y')=\frac{15}{25}=\frac{3}{5}

6 balls are drawn with replacementt.

Let Z be random variable that represents number of balls with Y mark on them in trial.

Z has binomail distribution with n=6.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(not\, more\, than\, 2\, bear\, Y) =P(Z\leq 2)

=P(Z=0)+P(Z=1)+P(Z=2)

=^6C_0 (\frac{2}{5})^{6} (\frac{3}{5})^0+^6C_1 (\frac{2}{5})^{5} (\frac{3}{5})^1+^6C_2 (\frac{2}{5})^{4} (\frac{3}{5})^2

= (\frac{2}{5})^{6} +6 (\frac{2}{5})^{5} (\frac{3}{5})^1+15 (\frac{2}{5})^{4} (\frac{3}{5})^2

= (\frac{2}{5})^{4} [(\frac{2}{5})^{2}+6 (\frac{2}{5}) (\frac{3}{5})+15(\frac{3}{5})^2]

= (\frac{2}{5})^{4} [\frac{4}{25}+\frac{36}{25}+\frac{135}{25}]

= (\frac{2}{5})^{4} [\frac{175}{25}]

= (\frac{2}{5})^{4} [7]

Question:5(iii) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

at least one ball will bear 'Y' mark.

Answer:

P(atleast\, one\, bear\, \, Y\, mark) =P(Z\geq 1)=1-P(Z=0)

=1-(\frac{2}{5})^6

Question:5(iv) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

the number of balls with 'X' mark and 'Y' mark will be equal.

Answer:

P(equal\, to\, the \, number\, of\, balls \, with \, X \, mark \, and\, Y \, mark )=P(Z=3)

P(Z=3)=^6C_3.(\frac{2}{5})^2.(\frac{3}{5})^3

P(Z=3)=\frac{20\times 8\times 27}{15625}

P(Z=3)=\frac{864}{3125}

Question:6 In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is \frac{5}{6} . What is the probability that he will knock down fewer than 2 hurdles?

Answer:

Let p and q respectively be probability that the player will clear and knock down the hurdle.

p=\frac{5}{6}

q=1-p=1-\frac{5}{6}=\frac{1}{6}

Let X represent random variable that represent number of times the player will knock down the hurdle.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(Z< 2)=P(Z=0)+P(Z=1)

=^{10}C_0 .( \frac{5}{6})^{10}.( \frac{1}{6})^{0}+^{10}C_1 .( \frac{5}{6})^{9}.( \frac{1}{6})^{1}

=( \frac{5}{6})^{10}+10.( \frac{5}{6})^{9}.( \frac{1}{6})

=( \frac{5}{6})^{9}( \frac{5}{6}+10\times . \frac{1}{6})

=( \frac{5}{6})^{9} \times \frac{5}{2}

=\frac{5^1^0}{2\times 6^9}

Question:7 A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.

Answer:

Probability of 6 in a throw of die =P

P=\frac{1}{6}

q=1-P=1-\frac{1}{6}=\frac{5}{6}

Probability that 2 sixes come in first five throw of die :

=^5C_2 (\frac{5}{6})^3 (\frac{1}{6})^2

=\frac{10\times 5^3}{6^5}

Probability that third six comes in sixth throw :

=\frac{10\times 5^3}{6^5}\times \frac{1}{6}

=\frac{10\times 125}{6^6}

=\frac{1250}{23328}

Question:8 If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?

Answer:

In a leap year, there are 366 days.

In 52 weeks, there are 52 Tuesdays.

The probability that a leap year will have 53 Tuesday is equal to the probability that the remaining 2 days are Tuesday.

The remaining 2 days can be :

1. Monday and Tuesday

2. Tuesday and Wednesday

3. Wednesday and Thursday

4. Thursday and Friday

5.friday and Saturday

6.saturday and Sunday

7.sunday and Monday

Total cases = 7.

Favorable cases = 2

Probability of having 53 Tuesday in a leap year = P.

P=\frac{2}{7}

Question:9 An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be atleast 4 successes.

Answer:

Probability of success is twice the probability of failure.

Let probability of failure be X

then Probability of success = 2X

Sum of probabilities is 1.

\therefore \, \, \, X+2X=1

\Rightarrow \, \, \, 3X=1

\Rightarrow \, \, \, X=\frac{1}{3}

Let P=\frac{1}{3} and q=\frac{2}{3}

Let X be random variable that represent the number of success in six trials.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X\geq 4)=P(X=4)+P(X=5)+P(X=6)

=^6C_4 \left [ \frac{2}{3} \right ]^4\left [ \frac{1}{3} \right ]^2+^6C_5 \left [ \frac{2}{3} \right ]^5\left [ \frac{1}{3} \right ]^1+^6C_6 \left [ \frac{2}{3} \right ]^6\left [ \frac{1}{3} \right ]^0

=\frac{15\times 2^4}{3^6}+\frac{6\times 2^5}{3^6}+\frac{2^6}{3^6}

=\frac{ 2^6}{3^6}(15+12+4)

=\frac{ 2^6}{3^6}(31)

=\frac{31}{9}\left [ \frac{2}{3} \right ]^4

Question:10 How many times must a man toss a fair coin so that the probability of having at least one head is more than 90^{o}/_{o} ?

Answer:

Let the man toss coin n times.

Probability of getting head in first toss = P

P=\frac{1}{2}

q=\frac{1}{2}

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

=^nC_x.\left ( \frac{1}{2} \right )^{n-x}.\left ( \frac{1}{2} \right )^x

P(getting\, atleast\, one\, head)> \frac{90}{100}

P(X\geq 1)> 0.9

1-P(X=0)> 0.9

1-^nC_0 \frac{1}{2^n}> 0.9

^nC_0 \frac{1}{2^n}< 0.1

\frac{1}{2^n}< 0.1

\frac{1}{0.1}< 2^n

10< 2^n

The minimum value to satisfy the equation is 4.

The man should toss a coin 4 or more times.

Question:11 In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins / loses.

Answer:

In a throw of die,

probability of getting six = P

P=\frac{1}{6}

probability of not getting six = q

q=1-P=1-\frac{1}{6}=\frac{5}{6}

There are three cases :

1. Gets six in the first throw, required probability is \frac{1}{6}

The amount he will receive is Re. 1

2.. Does not gets six in the first throw and gets six in the second throw, then the probability

=\frac{5}{6}\times \frac{1}{6}=\frac{5}{36}

The amount he will receive is - Re.1+ Re.1=0

3. Does not gets six in first 2 throws and gets six in the third throw, then the probability

=\frac{5}{6}\times\frac{5}{6}\times \frac{1}{6}=\frac{25}{216}

Amount he will receive is -Re.1 - Re.1+ Re.1= -1

Expected value he can win :

=1\times \frac{1}{6}+0\times \frac{5}{36}+(-1)\times \frac{25}{216}

= \frac{1}{6}-\frac{25}{216}

= \frac{11}{216}

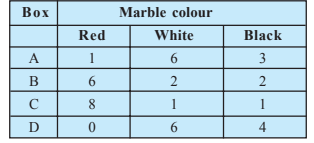
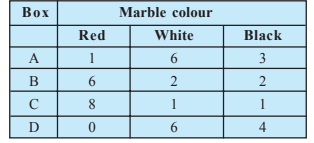
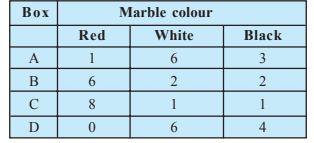
Question:12(i) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

1648018018261

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A ?

Answer:

1648018246557 '

Let R be the event of drawing red marble.

Let E_A,E_B,E_C respectively denote the event of selecting box A, B, C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box A is P(E_A|R)

P(E_A|R)=\frac{P(E_A\cap R)}{P(R)}

=\frac{\frac{1}{40}}{\frac{3}{8}}

=\frac{1}{15}

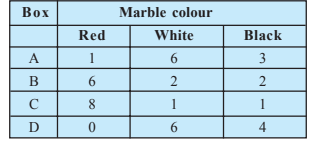
Question:12(ii) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

1648018297681

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box B?

Answer:

1648018367685

Let R be event of drawing red marble.

Let E_A,E_B,E_C respectivly denote event of selecting box A,B,C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box B is P(E_B|R)

P(E_B|R)=\frac{P(E_B\cap R)}{P(R)}

=\frac{\frac{6}{40}}{\frac{3}{8}}

=\frac{2}{5}

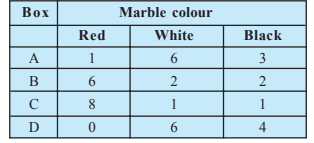
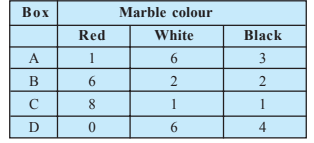
Question:12(iii) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

1648018414746

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box C?

Answer:

1648018436346

Let R be event of drawing red marble.

Let E_A,E_B,E_C respectivly denote event of selecting box A,B,C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box C is P(E_C|R)

P(E_C|R)=\frac{P(E_C\cap R)}{P(R)}

=\frac{\frac{8}{40}}{\frac{3}{8}}

=\frac{8}{15}

Question:13 Assume that the chances of a patient having a heart attack is 40^{o}/_{o}. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30^{o}/_{o} and prescription of certain drug reduces its chances by 25^{o}/_{o}. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?

Answer:

Let A,E1, E2 respectively denote the event that a person has a heart break, selected person followed the course of yoga and meditation , and the person adopted

the drug prescription.

\therefore \, \, \, \, P(A)=0.40

\therefore \, \, \, \, P(E1)=P(E2)=\frac{1}{2}

P(A|E1)=0.40\times 0.70=0.28

P(A|E2)=0.40\times 0.75=0.30

the probability that the patient followed a course of meditation and yoga is P(E1,A)

P(E1,A)=\frac{P(E1).P(E1|A)}{P(E1).P(E1|A)+P(E2).P(E2|A)}

P(E1,A)=\frac{0.5\times 0.28}{0.5\times 0.28 + 0.5\times 0.30}

=\frac{14}{29}

Question:14 If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability \frac{1}{2} ).

Answer:

Total number of determinant of second order with each element being 0 or 1 is 2^4=16

The values of determinant is positive in the following cases \begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}, \begin{bmatrix} 1 & 1\\ 0 & 1\end{bmatrix}, \begin{bmatrix} 1 & 0\\ 1 & 1\end{bmatrix}

Probability is

=\frac{3}{16}

Question:15(i) An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:

P(A fails) = 0.2

P(B fails alone) = 0.15

P(A and B fail) = 0.15

Evaluate the following probabilities

P(A \; fails\mid B\; has\; failed)

Answer:

Let event in which A fails and B fails be E_A,E_B

P(E_A)=0.2

P(E_A\, and \, E_B)=0.15

P(B\, fails\, alone)=P(E_B)-P(E_A\, and\, E_B)

\Rightarrow \, \, \, 0.15=P(E_B)-0.15

\Rightarrow \, \, \, P(E_B)=0.3

P(E_A|E_B)=\frac{P(E_A\cap E_B)}{P(E_B)}

=\frac{0.15}{0.3}=0.5

Question:15(ii) An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:

P(A fails) = 0.2

P(B fails alone) = 0.15

P(A and B fail) = 0.15

Evaluate the following probabilities

P(A\; fails \; alone)

Answer:

Let event in which A fails and B fails be E_A,E_B

P(E_A)=0.2

P(E_A\, and \, E_B)=0.15

P(B\, fails\, alone)=P(E_B)-P(E_A\, and\, E_B)

\Rightarrow \, \, \, 0.15=P(E_B)-0.15

\Rightarrow \, \, \, P(E_B)=0.3

P(A\, fails\, \, alone)=P(E_A)-P(E_A\, and\, E_B)

=0.2-0.15=0.05

Question:16 Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black.

Answer:

Let E1 and E2 respectively denote the event that red ball is transfered from bag 1 to bag 2 and a black ball is transfered from bag 1 to bag2.

P(E1)=\frac{3}{7} and P(E2)=\frac{4}{7}

Let A be the event that ball drawn is red.

When a red ball is transfered from bag 1 to bag 2.

P(A|E1)=\frac{5}{10}=\frac{1}{2}

When a black ball is transfered from bag 1 to bag 2.

P(A|E2)=\frac{4}{10}=\frac{2}{5}

P(E2|A)=\frac{P(E2).P(A|E2)}{P(E2).P(A|E2)+P(E1).P(A|E1)}

=\frac{\frac{4}{7}\times \frac{2}{5}}{\frac{4}{7}\times \frac{2}{5}+\frac{3}{7}\times \frac{1}{2}}

=\frac{16}{31}

Question:17 If A and B are two events such that P(A\neq 0) and P(B\mid A)=1, then

Choose the correct answer of the following:

(A) A\subset B

(B) B\subset A

(C) B=\phi

(D) A=\phi

Answer:

A and B are two events such that P(A\neq 0) and P(B\mid A)=1,

P(B|A)=\frac{P(B\cap A)}{P(A)}

1=\frac{P(B\cap A)}{P(A)}

P(B\cap A)=P(A)

\Rightarrow \, \, \, A\subset B

Option A is correct.

Question:18 If P(A\mid B)> P(A) , then which of the following is correct :

(A) P(B\mid A)< P(B)

(B) P(A\cap B)< P(A).P(B)

(C) P(B\mid A)> P(B)

(D) P(B\mid A)= P(B)

Answer:

P(A\mid B)> P(A)

\Rightarrow \, \, \frac{P(A\cap B)}{P(B)}> P(A)

\Rightarrow \, \, P(A\cap B)> P(A).P(B)

\Rightarrow \, \, \frac{P(A\cap B)}{P(A)}> P(B)

\Rightarrow \, \, P(B|A)> P(B)

Option C is correct.

Question:19 If A and B are any two events such that P(A)+P(B)-P(A \; and\; B)=P(A), then

(A) P(B\mid A)=1

(B) P(A\mid B)=1

(C) P(B\mid A)=0

(D) P(A\mid B)=0

Answer:

P(A)+P(B)-P(A \; and\; B)=P(A),

P(A)+P(B)-P(A\cap B)=P(A)

\Rightarrow \, \, \, P(B)-P(A\cap B)=0

\Rightarrow \, \, \, P(B)=P(A\cap B)

P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(B)}{P(B)}=1

Option B is correct.

The conditional probability of an event E, given the occurrence of the event F is given by

P(E|F)=\frac{Number\:of\:elementary\:events\:favourable\:to \:E\cap F}{Number\:of\:elementary\:events\:which\:are\:favourable\:to \:F}

If you are looking for probability class 12 ncert solutions of exercise then they are listed below.

Class 12 Maths Chapter 13 NCERT solutions: Insight

  • Generally, two questions( 8 marks) are asked from this chapter in 12th board final examination. You can score these 8 marks very easily with the help of probability Class 12 ncert solutions chapter 13.

  • In the NCERT textbook there are 37 solved examples are given, so you can understand the concept easily. In this chapter 13 12 th class, there is a total of 81 questions in 5 exercises. You should try to solve every question given in chapter 13 class 12 maths on your own.

  • If you are not able to do, you can take the help of these NCERT solutions for class 12 maths chapter 13 probability. These probability class 12 NCERT questions are solved and explained in a step-by-step manner, so it can be understood very easily.

  • This chapter 13 12 th class requires lots of practice to understand it better. So, you are advised to solve miscellaneous exercise of probability class 12 ncert solutions.

NCERT class 12 maths chapter 13 Solutions Probability - Topics

13.1 Introduction

13.2 Conditional Probability

13.2.1 Properties of conditional probability

13.3 Multiplication Theorem on Probability

13.4 Independent Events

13.5 Bayes' Theorem

13.5.1 Partition of a sample space

3.5.2 Theorem of total probability

13.6 Random Variables and its Probability Distributions

13.6.1 Probability distribution of a random variable

13.6.2 Mean of a random variable

13.6.3 Variance of a random variable

13.7 Bernoulli Trials and Binomial Distribution

13.7.1 Bernoulli trials

13.7.2 Binomial distribution

NCERT solutions for class 12 maths - Chapter Wise

chapter 1NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
chapter 2NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
chapter 3NCERT solutions for class 12 maths chapter 3 Matrices
chapter 4NCERT solutions for class 12 maths chapter 4 Determinants
chapter 5NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
chapter 6NCERT solutions for class 12 maths chapter 6 Application of Derivatives
chapter 7NCERT solutions for class 12 maths chapter 7 Integrals
chapter 8NCERT solutions for class 12 maths chapter 8 Application of Integrals
chapter 9NCERT solutions for class 12 maths chapter 9 Differential Equations
chapter 10NCERT solutions for class 12 maths chapter 10 Vector Algebra
chapter 11NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
chapter 12NCERT solutions for class 12 maths chapter 12 Linear Programming
chapter 13NCERT solutions for class 12 maths chapter 13 Probability
SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Key Features of NCERT Solutions for Class 12 Maths Chapter 13 Probability

Comprehensive explanations: The probability ncert class 12 solutions provided in NCERT Solutions for Class 12 Maths Chapter 13 Probability are explained in a comprehensive and step-by-step manner. This helps students to understand the concepts better and makes it easy for them to solve similar problems.

Easy to understand: The probability solutions class 12 are written in simple language, making it easy for students to understand and learn the concepts. The solutions are designed to cater to the needs of students of all learning levels.

Covers all the topics: The class 12 probability solutions cover all the topics in Chapter 13 Probability of Class 12 Maths. This helps students to have a comprehensive understanding of the chapter.

Exercise-wise solutions: The class 12 chapter 13 maths solutions are provided exercise-wise, which helps students to focus on specific problems and concepts that they find difficult.

Examples and illustrations: The ch 13 maths class 12 solutions include examples and illustrations to explain the concepts and solutions better. These examples help students to understand the applications of probability in real-life situations.

NCERT solutions for class 12 subject wise

NCERT Solutions class wise

NCERT Books and NCERT Syllabus

Benefits of NCERT solutions

  • As this chapter has 10% weightage in 12th board final exam. NCERT solutions for class 12 maths chapter 13 probability will help you to score good marks in the final exam.

  • NCERT solutions for Class 12 Maths Chapter 13 are very easy to understand as these are prepared and explained in a detailed manner.

  • At the end of every chapter, there is an additional exercise called Miscellaneous exercise which is very important for you if you wish to develop a grip on the concepts. In NCERT solutions for class 12 maths chapter 13 probability, you will get solutions for miscellaneous exercise too.

  • These NCERT solutions for Class 12 Maths Chapter 13 PDF download are prepared with different approaches so it will give you new ways of solving the problems.

  • NCERT solutions for class 12 maths chapter 13 probability are prepared and explained by the experts who know how best to answer the questions in the board exam. So, it will help you to score good marks in the exam.

NCERT Exemplar Class 12 Solutions

Happy Reading !!!

Frequently Asked Question (FAQs)

1. What are the important topics in chapter probability?

Basic probability, conditional probability, properties of conditional probability, multiplication theorem on probability, independent events, Bayes' theorem, random variables, and its probability distributions, Bernoulli trials, and Binomial distribution are important topics of this chapter.

2. Does CBSE provides the solutions of NCERT for class 12 maths Chapter 13?

No, CBSE doesn’t provide NCERT solutions for any class or subject. but there are so many coaching institutions which provide solutions freely. if you are interested then you can download these from careers360 official website.

3. Which are the most difficult chapters of NCERT Class 12 Maths syllabus?

Students consider integration and application of integration as the most difficult chapters in CBSE class 12 maths but with rigorous practice, you will get conceptual clarity and will be able to have a strong grip on them also.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 29 January,2024
i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer
Upasana Barman 24 August,2022
i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.


As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.


Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.


Believe in Yourself! You can make anything happen


All the very best.

Read Complete Answer
Mayankjha.student2007 23 August,2022
if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects  and  we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer
Nuthalapati Vyshnavi 21 August,2022
I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer
Muskan Dhalwal 17 August,2022
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
March 22, 2024 - 08:10 PM IST :
February 02, 2024 - 03:48 PM IST :
January 04, 2024 - 06:06 PM IST :
CBSE Results 2024: Last 9 years’ CBSE Class 10, 12 result date and time; links to check score
May 01, 2024 - 03:34 PM IST
CBSE Board exams twice a year from 2025, no plan for semesters: MoE
April 26, 2024 - 07:45 PM IST
CBSE Class 12 board exams 2025 to have 50% competency-based questions; no change in 10th
April 04, 2024 - 03:43 PM IST
CBSE Class 12 board exams 2024 over; expected result date, trends of last 10 years
April 02, 2024 - 04:40 PM IST
CBSE Class 12 accountancy board exam analysis 2024 out; paper rated easy, balanced
March 23, 2024 - 05:04 PM IST
CBSE Class 12 biology paper 2024 today; know marking scheme, important topics
March 19, 2024 - 07:54 AM IST
CBSE Class 12 Exam 2024 Live: CBSE 12th Biology paper analysis, answer key, passing marks, result updates
March 18, 2024 - 05:29 PM IST

Stay up-to date with CBSE Class 12th News

Back to top