Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • Consider a sphere of radius R with charge density distributed as ρ(r) = kr for r ≤ R = 0 for r >R . a) Find the electric field at all points r.

Consider a sphere of radius R with charge density distributed as

\rho (r) = kr for r \leq R\\ = 0\: f\! or \: r >R .
a) Find the electric field at all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero? Assume that the introduction of the proton does not alter the negative charge distribution.

Answers (1)

a) The charge density distribution expression in the sphere tells that the electric field is radial.

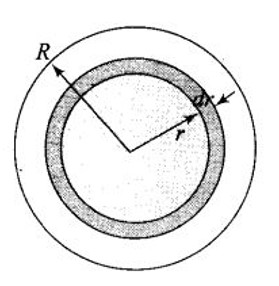
Let us consider a sphere S of radius R and two hypothetic spheres of radius r< R and r> R.
Let us first consider for point r< R, electric field intensity will be given by,

\oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho \: dV

Here dV =4\pi r^2\:dr

\Rightarrow \oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}4 \pi K \int_{0}^{r}r^3dr\left ( \because \rho \left ( r \right )=Kr \right )

\Rightarrow \left ( E \right )4 \pi r^2= \frac{4 \pi K}{\varepsilon _0}\frac{r^4}{4}

We get  

E= \frac{1}{4\varepsilon _0}Kr^2

As charge density is positive, it means the direction of E is radially outwards.
 

Now consider points r>R , electric field intensity will be given by

                \oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho dV

            \Rightarrow E(4 \pi r^2)= \frac{4 \pi K}{\varepsilon _0}\int_{0}^{R}r^3dr=\frac{4 \pi K}{\varepsilon _0}\frac{R^4}{4}

Which gives     E=\frac{K}{4 \varepsilon _0}\frac{R^4}{r^2}

Here also the charge density is again positive. So, the direction of E is radially outward.

(b) The two proton must be placed symmetrically on the opposite sides of the centre along a diameter. This can be shown by
the figure given below. Charge on the sphere,

\\q=\int_{0}^{R}\rho dV= \int_{0}^{R}\left ( Kr \right )4 \pi r^2dr\\ \\ q=4 \pi K\frac{R^4}{4}2e\\ \\\because K=\frac{2e}{\pi R^4}

 

The proton 1 and 2 are embedded at distance r from the centre of the sphere as shown, then attractive force on proton 1 due to charge
distribution is

F_1=eE=\frac{-eKr^2}{4\varepsilon _0}
and repulsive force on proton 1 due to proton 2 is

F_2=\frac{e^2}{4 \pi\varepsilon _0 (2r)^2}

Net force on proton 1, F=F_1+F_2

F=\frac{-eKr^2}{4\varepsilon _0}+\frac{e^2}{16 \pi \varepsilon _0r^2}

Thus, net force on proton 1 will be zero, when

        \frac{er^22e}{4\varepsilon _0 \pi R^4}= \frac{e^2}{16 \pi \varepsilon _0r^2}

\Rightarrow r^4= \frac{R^4}{8}

Hence the protons must be at a distance r=\frac{R}{(8)^{1/4}} from the centre.

 

Posted by

infoexpert21

View full answer

Similar Questions

Latest Question