Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.

Total charge –Q is uniformly spread along the length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.

(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.

Answers (1)

Let the charge q is displaced slightly by z\left ( z< < R \right ) along the axis of ring. Let force on the charge q will be towards O. The motion of charge q will be simple harmonic, it the force on charge q must be proportion to z and is directed towards O.

Electric field at axis of the ring at a distance z from the centre of ring

E=\frac{1}{4\pi \varepsilon _0}\frac{Q_z}{\left ( R^2+Z^2 \right )^{3/2}};towords O
the net force on the charge F_{net}=qE                    

                    F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{\left ( R^2+Z^2 \right )^{3/2}};
\Rightarrow                F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}}

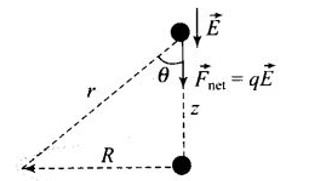
As z<<R\: then,

\Rightarrow                F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}} or \vec{F}_{net}=-K\vec{z}

Where K=\frac{Qq}{4\pi \varepsilon _{0}R^{3}}=constant

Clearly, the force on q is proportional to the negative of its displacement. Therefore the motion of q is simple harmonic.

\\\omega \sqrt{\frac{K}{m}}\: and\: T=\frac{2\pi}{\omega }=2\pi\sqrt{\frac{m}{K}}\\T=2\pi\sqrt{\frac{m4\pi \varepsilon _0\: R^3}{Qq}} \\T=2\pi\sqrt{\frac{4\pi \varepsilon _0\: m\: R^3}{Qq}} \\

 

 

Posted by

infoexpert21

View full answer

Similar Questions

Latest Question