NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations

Q: How the NCERT solutions are helpful in the board exam ?

As CBSE board exam paper is designed entirely based on NCERT textbooks and most of the questions in CBSE board exam are directly asked from NCERT textbook, students must know the NCERT very well to perform well in the exam. Only knowing the answer it not enough to perform well in the exam. In the NCERT solutions students will get know how best to write answer in the board exam in order to get good marks.

Q: What is the weightage of the chapter Differential Equations for CBSE board exam ?

Generally, one question of 5 marks is asked from this chapter in the 12 th board final exam. you should refer NCER syllabus for it. NCERT textbook and NCERT Notes are recommended if you want to obtain meritious marks in the Board exam.

Q: What are the important topics in chapter Differential Equations ?

Basic concepts of differential equation, o rder and degree of the differential equation, gen eral and particular solutions of a differential equation, f ormation of a differential equation, m ethods of solving first order,first degree differential equations, ho mogeneous differential equations and l inear differential equations are the important topics of this chapter.

Q: Are the answers to all the textbook questions available in the differential equations ncert solutions maths class 12 chapter 9?

The NCERT class 12 maths differential equations are available in PDF format and have been created by subject experts in line with the textbook questions. These solutions for ch 9 maths class 12 adhere to the latest CBSE Syllabus for 2023 and encompass all the significant concepts for the board exam. The problems in the textbook are solved step by step in accordance with the marks weightage in the CBSE Board exams. Careers360 website offers both chapter-wise and exercise-wise PDF links that can be used by students to instantly clarify their doubts.

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations

Edited By Ramraj Saini | Updated on Sep 14, 2023 10:22 PM IST | #CBSE Class 12th

NCERT Differential Equations Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations are provided here. In class 11th, you have already learned how to differentiate a given function (f) with respect to an independent variable. In this article, you will get NCERT solutions for class 12 maths chapter 9 for all major topics of NCERT Class 12 maths syllabus. The equation of function and its one or more derivatives is called a differential equation.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Differential Equations Class 12 Questions And Answers
NCERT Differential Equations Class 12 Questions And Answers PDF Free Download
NCERT Differential Equations Class 12 Questions And Answers - Important Formulae
NCERT Differential Equations Class 12 Questions And Answers (Intext Questions and Exercise)
More About NCERT Solutions for Class 12 Maths Chapter 9
Differential Equations Class 12 - Topics
NCERT Exemplar Class 12 Solutions - Subject Wise
NCERT solutions for class 12 maths - Chapter Wise
NCERT solutions for class 12 subject wise
NCERT Solutions class wise
NCERT Books and NCERT Syllabus

In this differential equations class 12 questions and answers, some basic concepts related to the differential equations solutions, particular solutions, and general solutions of differential equations class 12 will be comprehensively discussed. In NCERT solutions for chapter 9 class 12 maths, questions from all these topics are covered in this article. If you are interested in other subjects then you can refer to NCERT solutions for class 12

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.

Apply Now

You will also learn some methods to find the differential equations solutions, the formation of differential equations class 12, and applications of differential equations in different areas in this NCERT class 12 maths chapter 9 question answer are also explained in details. Questions related to these topics are also covered in the NCERT solutions for class 12 maths ch 9 differential equations article. You can refer to NCERT solutions from classes 6 to 12 to learn CBSE maths and science.

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Also read :

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

NCERT Differential Equations Class 12 Questions And Answers PDF Free Download

Download PDF

NCERT Differential Equations Class 12 Questions And Answers - Important Formulae

>> Ordinary Differential Equations (ODEs): Ordinary Differential Equations involve derivatives of a function concerning a single independent variable. They are commonly used to model dynamic systems and phenomena.

>> Partial Differential Equations (PDEs): Partial Differential Equations involve derivatives of a function concerning multiple independent variables. They are frequently used in physics to describe phenomena like heat diffusion, wave propagation, and fluid dynamics.

>> Types of Differential Equations: Differential equations can be categorised based on their order, linearity, and specific properties. Common types include:

First-Order Differential Equations
Second-Order Differential Equations
Linear Differential Equations
Nonlinear Differential Equations
Homogeneous Differential Equations
Non-Homogeneous Differential Equations

SAT® | CollegeBoard

Apply

TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

>> Methods for Solving Differential Equations: Various techniques can be employed to solve differential equations, including:

Separation of Variables
Integrating Factors
Exact Differential Equations
Linear Differential Equations with Constant Coefficients
Method of Undetermined Coefficients
Variation of Parameters
Laplace Transforms

>> Applications of Differential Equations: Differential equations have widespread applications in science and engineering. Some examples include modelling population growth, describing electrical circuits, predicting radioactive decay, and simulating fluid flow.

Free download NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations for CBSE Exam.

NCERT Differential Equations Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT differential equations class 12 solutions - Exercise: 9.1

Question:1 Determine order and degree (if defined) of differential equation $\frac{\mathrm{d} ^4y}{\mathrm{d} x^4} +\sin(y''')=0$

Answer:

Given function is
$\frac{\mathrm{d} ^4y}{\mathrm{d} x^4} +\sin(y''')=0$
We can rewrite it as
$y^{''''}+\sin(y''') =0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''''}$

Therefore, the order of the given differential equation $\frac{\mathrm{d} ^4y}{\mathrm{d} x^4} +\sin(y''')=0$ is 4
Now, the given differential equation is not a polynomial equation in its derivatives
Therefore, it's a degree is not defined

Question:2 Determine order and degree (if defined) of differential equation $y' + 5y = 0$

Answer:

Given function is
$y' + 5y = 0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{'}$
Therefore, the order of the given differential equation $y' + 5y = 0$ is 1
Now, the given differential equation is a polynomial equation in its derivatives and its highest power raised to y ' is 1
Therefore, it's a degree is 1.

Question:3 Determine order and degree (if defined) of differential equation $\left(\frac{\mathrm{d} s}{\mathrm{d} t} \right )^4 + 3s \frac{\mathrm{d}^2 s}{\mathrm{d} t^2} = 0$

Answer:

Given function is
$\left(\frac{\mathrm{d} s}{\mathrm{d} t} \right )^4 + 3s \frac{\mathrm{d}^2 s}{\mathrm{d} t^2} = 0$
We can rewrite it as
$(s^{'})^4+3s.s^{''} =0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $s^{''}$

Therefore, the order of the given differential equation $\left(\frac{\mathrm{d} s}{\mathrm{d} t} \right )^4 + 3s \frac{\mathrm{d}^2 s}{\mathrm{d} t^2} = 0$ is 2
Now, the given differential equation is a polynomial equation in its derivatives and power raised to s '' is 1
Therefore, it's a degree is 1

Question:4 Determine order and degree (if defined) of differential equation.

$\left(\frac{d^2y}{dx^2} \right )^2 + \cos\left(\frac{dy}{dx} \right )= 0$

Answer:

Given function is
$\left(\frac{d^2y}{dx^2} \right )^2 + \cos\left(\frac{dy}{dx} \right )= 0$
We can rewrite it as
$(y^{''})^2+\cos y^{''} =0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}$

Therefore, the order of the given differential equation $\left(\frac{d^2y}{dx^2} \right )^2 + \cos\left(\frac{dy}{dx} \right )= 0$ is 2
Now, the given differential equation is not a polynomial equation in its derivatives
Therefore, it's a degree is not defined

Question:5 Determine order and degree (if defined) of differential equation.

$\frac{d^2y}{dx^2} = \cos 3x + \sin 3x$

Answer:

Given function is
$\frac{d^2y}{dx^2} = \cos 3x + \sin 3x$
$\Rightarrow \frac{d^2y}{dx^2}- \cos 3x - \sin 3x = 0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}\left ( \frac{d^2y}{dx^2} \right )$

Therefore, order of given differential equation $\frac{d^2y}{dx^2}- \cos 3x - \sin 3x = 0$ is 2
Now, the given differential equation is a polynomial equation in it's dervatives $\frac{d^2y}{dx^2}$ and power raised to $\frac{d^2y}{dx^2}$ is 1
Therefore, it's degree is 1

Question:6 Determine order and degree (if defined) of differential equation $(y''')^2 + (y'')^3 + (y')^4 + y^5= 0$

Answer:

Given function is
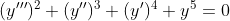(y''')^2 + (y'')^3 + (y')^4 + y^5= 0 Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{'''}$

Therefore, order of given differential equation 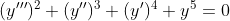is 3 Now, the given differential equation is a polynomial equation in it's dervatives $y^{'''} , y^{''} \ and \ y^{'}$ and power raised to $y^{'''}$ is 2
Therefore, it's degree is 2

Question:7 Determine order and degree (if defined) of differential equation

$y''' + 2y'' + y' =0$

Answer:

Given function is
$y''' + 2y'' + y' =0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{'''}$

Therefore, order of given differential equation $y''' + 2y'' + y' =0$ is 3
Now, the given differential equation is a polynomial equation in it's dervatives $y^{'''} , y^{''} \ and \ y^{'}$ and power raised to $y^{'''}$ is 1
Therefore, it's degree is 1

Question:8 Determine order and degree (if defined) of differential equation

$y' + y = e^x$

Answer:

Given function is
$y' + y = e^x$
$\Rightarrow$ $y^{'}+y-e^x=0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{'}$

Therefore, order of given differential equation $y^{'}+y-e^x=0$ is 1
Now, the given differential equation is a polynomial equation in it's dervatives $y^{'}$ and power raised to $y^{'}$ is 1
Therefore, it's degree is 1

Question:9 Determine order and degree (if defined) of differential equation

$y'' + (y')^2 + 2y = 0$

Answer:

Given function is
$y'' + (y')^2 + 2y = 0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}$

Therefore, order of given differential equation $y'' + (y')^2 + 2y = 0$ is 2
Now, the given differential equation is a polynomial equation in it's dervatives $y^{''} \ and \ y^{'}$ and power raised to $y^{''}$ is 1
Therefore, it's degree is 1

Question:10 Determine order and degree (if defined) of differential equation

$y'' + 2y' + \sin y = 0$

Answer:

Given function is
$y'' + 2y' + \sin y = 0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}$

Therefore, order of given differential equation $y'' + 2y' + \sin y = 0$ is 2
Now, the given differential equation is a polynomial equation in it's dervatives $y^{''} \ and \ y^{'}$ and power raised to $y^{''}$ is 1
Therefore, it's degree is 1

Question:11 The degree of the differential equation $\left(\frac{d^2y}{dx^2} \right )^3 + \left(\frac{dy}{dx} \right )^2 + \sin\left(\frac{dy}{dx}\right ) + 1= 0$ is

(A) 3

(B) 2

(D) not defined

Answer:

Given function is
$\left(\frac{d^2y}{dx^2} \right )^3 + \left(\frac{dy}{dx} \right )^2 + \sin\left(\frac{dy}{dx}\right ) + 1= 0$
We can rewrite it as
$(y^{''})^3+(y^{'})^2+\sin y^{'}+1=0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}$

Therefore, order of given differential equation $\left(\frac{d^2y}{dx^2} \right )^3 + \left(\frac{dy}{dx} \right )^2 + \sin\left(\frac{dy}{dx}\right ) + 1= 0$ is 2
Now, the given differential equation is a not polynomial equation in it's dervatives
Therefore, it's degree is not defined

Therefore, answer is (D)

Question:12 The order of the differential equation $2x^2\frac{d^2y}{dx^2} - 3\frac{dy}{dx} + y = 0$ is

(A) 2

(B) 1

(D) Not Defined

Answer:

Given function is
$2x^2\frac{d^2y}{dx^2} - 3\frac{dy}{dx} + y = 0$
We can rewrite it as
$2x.y^{''}-3y^{'}+y=0$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y^{''}$

Therefore, order of given differential equation $2x^2\frac{d^2y}{dx^2} - 3\frac{dy}{dx} + y = 0$ is 2

Therefore, answer is (A)

NCERT differential equations class 12 solutions - Exercise: 9.2

Question:1 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = e^x + 1 \qquad :\ y'' -y'=0$

Answer:

Given,

$y = e^x + 1$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d}e^x }{\mathrm{d} x} = e^x$

Again, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y' }{\mathrm{d} x} = \frac{\mathrm{d}e^x }{\mathrm{d} x} = e^x$

$\implies y'' = e^x$

Substituting the values of y’ and y'' in the given differential equations,

y'' - y' = e ^x - e ^x = 0 = RHS.

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = x^2 + 2x + C\qquad:\ y' -2x - 2 =0$

Answer:

Given,

$y = x^2 + 2x + C$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(x^2 + 2x + C) = 2x + 2$

Substituting the values of y’ in the given differential equations,

$y' -2x - 2 =2x + 2 - 2x - 2 = 0= RHS$ .

Therefore, the given function is the solution of the corresponding differential equation.

Question:3. Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = \cos x + C\qquad :\ y' + \sin x = 0$

Answer:

Given,

$y = \cos x + C$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(cosx + C) = -sinx$

Substituting the values of y’ in the given differential equations,

$y' - \sin x = -sinx -sinx = -2sinx \neq RHS$ .

Therefore, the given function is not the solution of the corresponding differential equation.

Question:4. Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = \sqrt{1 + x^2}\qquad :\ y' = \frac{xy}{1 + x^2}$

Answer:

Given,

$y = \sqrt{1 + x^2}$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(\sqrt{1 + x^2}) = \frac{2x}{2\sqrt{1 + x^2}} = \frac{x}{\sqrt{1 + x^2}}$

Substituting the values of y in RHS,

$\frac{x\sqrt{1+x^2}}{1 + x^2} = \frac{x}{\sqrt{1+x^2}} = LHS$ .

Therefore, the given function is a solution of the corresponding differential equation.

Question:5 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = Ax\qquad :\ xy' = y\;(x\neq 0)$

Answer:

Given,

$y = Ax$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(Ax) = A$

Substituting the values of y' in LHS,

$xy' = x(A) = Ax = y = RHS$ .

Therefore, the given function is a solution of the corresponding differential equation.

Question:6. Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = x\sin x\qquad :\ xy' = y + x\sqrt{x^2 - y^2}\ (x\neq 0\ \textup{and} \ x > y\ or \ x < -y)$

Answer:

Given,

$y = x\sin x$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(xsinx) = sinx + xcosx$

Substituting the values of y' in LHS,

$xy' = x(sinx + xcosx)$

Substituting the values of y in RHS.

$\\xsinx + x\sqrt{x^2 - x^2sin^2x} = xsinx + x^2\sqrt{1-sinx^2} = x(sinx+xcosx) = LHS$

Therefore, the given function is a solution of the corresponding differential equation.

Question:7 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$xy = \log y + C\qquad :\ y' = \frac{y^2}{1 - xy}\ (xy\neq 1)$

Answer:

Given,

$xy = \log y + C$

Now, differentiating both sides w.r.t. x,

$\\ y + x\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(logy) = \frac{1}{y}\frac{\mathrm{d}y }{\mathrm{d} x}\\ \\ \implies y^2 + xyy' = y' \\ \\ \implies y^2 = y'(1-xy) \\ \\ \implies y' = \frac{y^2}{1-xy}$

Substituting the values of y' in LHS,

$y' = \frac{y^2}{1-xy} = RHS$

Therefore, the given function is a solution of the corresponding differential equation.

Question:8 In each of the Exercises 1 to 10 verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y - cos y = x \qquad :(\ y\sin y + \cos y + x) y' = y$

Answer:

Given,

$y - cos y = x$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d}y }{\mathrm{d} x} +siny\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x}(x) = 1$

$\implies$ y' + siny.y' = 1

$\implies$ y'(1 + siny) = 1

$\implies y' = \frac{1}{1+siny}$

Substituting the values of y and y' in LHS,

$(\ (x+cosy)\sin y + \cos y + x) (\frac{1}{1+siny})$

$= [x(1+siny) + cosy(1+siny)]\frac{1}{1+siny}$

= (x + cosy) = y = RHS

Therefore, the given function is a solution of the corresponding differential equation.

Question:9 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$x + y = \tan^{-1}y\qquad :\ y^2y' + y^2 + 1 = 0$

Answer:

Given,

$x + y = \tan^{-1}y$

Now, differentiating both sides w.r.t. x,

$\\ 1 + \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{1}{1 + y^2}\frac{\mathrm{d} y}{\mathrm{d} x}\\ \\ \implies1+y^2 = y'(1-(1+y^2)) = -y^2y' \\ \implies y' = -\frac{1+y^2}{y^2}$

Substituting the values of y' in LHS,

$y^2(-\frac{1+y^2}{y^2}) + y^2 + 1 = -1- y^2+ y^2 +1 = 0 = RHS$

Therefore, the given function is a solution of the corresponding differential equation.

Question:10 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

$y = \sqrt{a^2 - x^2}\ x\in (-a,a)\qquad : \ x + y \frac{dy}{dx} = 0\ (y\neq 0)$

Answer:

Given,

$y = \sqrt{a^2 - x^2}$

Now, differentiating both sides w.r.t. x,

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{\mathrm{d}}{\mathrm{d} x}(\sqrt{a^2 - x^2}) = \frac{-2x}{2\sqrt{a^2 - x^2}} = \frac{-x}{\sqrt{a^2 - x^2}}$

Substituting the values of y and y' in LHS,

$x + y \frac{dy}{dx} = x + (\sqrt{a^2 - x^2})(\frac{-x}{\sqrt{a^2 - x^2}}) = 0 = RHS$

Therefore, the given function is a solution of the corresponding differential equation.

Question:11 The number of arbitrary constants in the general solution of a differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4

Answer:

(D) 4

The number of constants in the general solution of a differential equation of order n is equal to its order.

Question:12 The number of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3
(B) 2
(C) 1
(D) 0

Answer:

(D) 0

In a particular solution of a differential equation, there is no arbitrary constant.

Differential Equations Class 12 NCERT Solutions - Exercise: 9.3

Question:1 Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.

$\frac{x}{a} + \frac{y}{b} = 1$

Answer:

Given equation is

$\frac{x}{a} + \frac{y}{b} = 1$
Differentiate both the sides w.r.t x
$\frac{d\left ( \frac{x}{a}+\frac{y}{b} \right )}{dx}=\frac{d(1)}{dx}$
$\frac{1}{a}+\frac{1}{b}.\frac{dy}{dx} = 0\\ \frac{dy}{dx} = -\frac{b}{a}$
Now, again differentiate it w.r.t x
$\frac{d^2y}{dx^2} =0$
Therefore, the required differential equation is $\frac{d^2y}{dx^2} =0$ or $y^{''} =0$

Question:2 Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.

$y^2 = a(b^2 - x^2)$

Answer:

Given equation is
$y^2 = a(b^2 - x^2)$
Differentiate both the sides w.r.t x
$\frac{d\left ( y^2 \right )}{dx}=\frac{d(a(b^2-x^2))}{dx}$
$2y\frac{dy}{dx}= -2ax\\ \\ y.\frac{dy}{dx}= -ax\\ \\ y.y^{'}=-ax$ -(i)
Now, again differentiate it w.r.t x
$y^{'}.y^{'}+y.y^{''}= -a\\ (y^{'})^2+y.y^{''}=-a$ -(ii)
Now, divide equation (i) and (ii)
$\frac{(y^{'})^2+y.y^{''}}{y.y^{'}}= \frac{-a}{-ax}\\ \\ x(y^{'})^2+x.y.y^{''}=y.y^{'}\\ \\ x(y^{'})^2+x.y.y^{''}-y.y^{'}=0$
Therefore, the required differential equation is $x(y^{'})^2+x.y.y^{''}-y.y^{'}=0$

Question:3 Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b. $y = ae^{3x} + b e^{-2x}$

Answer:

Given equation is
$y = ae^{3x} + b e^{-2x}$ -(i)
Differentiate both the sides w.r.t x
$\frac{d\left ( y \right )}{dx}=\frac{d(ae^{3x}+be^{-2x})}{dx}$
$y^{'}=\frac{dy}{dx}= 3ae^{3x}-2be^{-2x}\\ \\$ -(ii)
Now, again differentiate w.r.t. x
$y^{''}= \frac{d^2y}{dx^2} = 9ae^{3x}+4be^{-2x}$ -(iii)
Now, multiply equation (i) with 2 and add equation (ii)
$2(ae^{3x}+be^{-2x})+(3a-2be^{-x}) = 2y+y^{'}\\ 5ae^{3x} = 2y+y^{'}\\ ae^{3x}= \frac{2y+y^{'}}{5}$ -(iv)
Now, multiply equation (i) with 3 and subtract from equation (ii)
$3(ae^{3x}+be^{-2x})-(3a-2be^{-x}) = 3y-y^{'}\\ 5be^{-2x} = 3y-y^{'}\\ be^{-2x}= \frac{3y-y^{'}}{5}$ -(v)
Now, put values from (iv) and (v) in equation (iii)
$y^{''}= 9.\frac{2y+y^{'}}{5}+4.\frac{3y-y^{'}}{5}\\ \\ y^{''}= \frac{18y+9y^{'}+12y-4y^{'}}{5}\\ \\ y^{''}= \frac{5(6y-y^{'})}{5}=6y-y^{'}\\ \\ y^{''}+y^{'}-6y=0$

Therefore, the required differential equation is $y^{''}+y^{'}-6y=0$

Question:4 Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b. $y = e^{2x}(a+bx)$

Answer:

Given equation is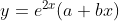
$y = e^{2x}(a+bx)$ -(i)
Now, differentiate w.r.t x
$\frac{dy}{dx}= \frac{d(e^{2x}(a+bx))}{dx}= 2e^{2x}(a+bx)+e^{2x}.b$ -(ii)
Now, again differentiate w.r.t x
$y^{''}= \frac{d^2y}{dx^2}= \frac{d}{dx}\frac{dy}{dx} = 4e^{2x}(a+bx)+2be^{2x}+2be^{2x}= 4e^{2x}(a+bx)+4be^{2x}$ -(iii)
Now, multiply equation (ii) with 2 and subtract from equation (iii)
$4e^{2x}(a+bx)+4be^{2x}-2\left ( 2e^{2x}(a+bx)+be^{2x} \right )=y^{''}-2y^{'}\\ \\ 2be^{2x} = y^{''}-2y^{'}\\ \\ be^{2x}= \frac{y^{''}-2y^{'}}{2}$ -(iv)
Now,put the value in equation (iii)
$y^{''}=4y+4.\frac{y^{''}-2y^{'}}{2}\\ \\ y^{''}= 4y+2y^{''}-4y^{'}\\ \\ y^{''}-4y^{'}+4y=0$
Therefore, the required equation is $y^{''}-4y^{'}+4y=0$

Question:5 Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.

$y=e^x(a\cos x + b\sin x)$

Answer:

Given equation is
$y=e^x(a\cos x + b\sin x)$ -(i)
Now, differentiate w.r.t x
$\frac{dy}{dx}= \frac{d(e^{x}(a\cos x+b\sin x))}{dx}= e^{x}(a\cos x+b\sin x)+e^x(-a\sin x+b\cos x )$ -(ii)
Now, again differentiate w.r.t x
$y^{''}= \frac{d^2y}{dx^2}= \frac{d}{dx}\frac{dy}{dx} =e^{x}(a\cos x+b\sin x)+e^x(-a\sin x+b\cos x )$ $+e^x(-a\sin x+b\cos x )+e^x(-a\cos x-b\sin x)$
$=2e^x(-a\sin x+b\cos x )$ -(iii)
Now, multiply equation (i) with 2 and multiply equation (ii) with 2 and add and subtract from equation (iii) respectively
we will get

$y^{''}-2y^{'}+2y = 0$
Therefore, the required equation is $y^{''}-2y^{'}+2y = 0$

Question:6 Form the differential equation of the family of circles touching the y-axis at origin.

Answer:

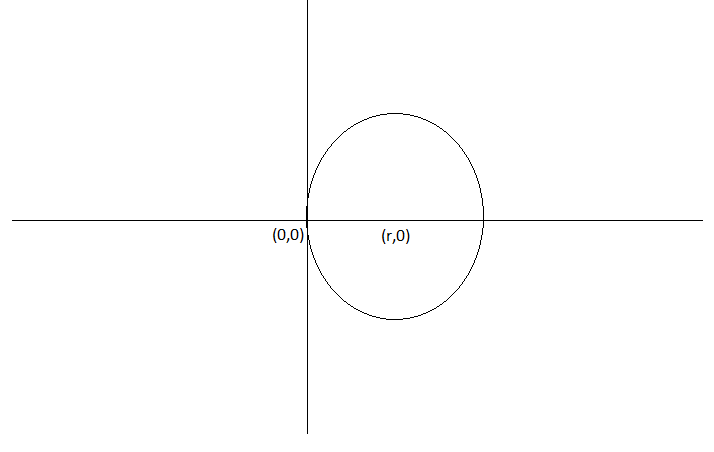1628484808301 If the circle touches y-axis at the origin then the centre of the circle lies at the x-axis
Let r be the radius of the circle
Then, the equation of a circle with centre at (r,0) is
$(x-r)^2+(y-0)^2 = r^2$
$x^2+r^2-2xr+y^2=r^2\\ x^2+y^2-2xr=0$ -(i)
Now, differentiate w.r.t x
$2x+2y\frac{dy}{dx}-2r=0\\ y\frac{dy}{dx}\Rightarrow yy^{'}+x-r=0$
$yy^{'}+x=r$ -(ii)
Put equation (ii) in equation (i)
$x^2+y^2=2x(yy^{'}+x)\\ y^2=2xyy^{'}+x^2$
Therefore, the required equation is $y^2=2xyy^{'}+x^2$

Question:7 Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.

Answer:

Equation of perabola having vertex at origin and axis along positive y-axis is
$x^2= 4ay$ (i)
Now, differentiate w.r.t. c
$2x= 4a\frac{dy}{dx}\\ \\ \frac{dy}{dx} =y^{'}= \frac{x}{2a}$
$a=\frac{x}{2y^{'}}$ -(ii)
Put value from equation (ii) in (i)
$x^2= 4y.\frac{x}{2y^{'}}\\ xy^{'}-2y = 0$
Therefore, the required equation is $xy^{'}-2y = 0$

Question:8 Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.

Answer:

Equation of ellipses having foci on y-axis and centre at origin is
$\frac{x^2}{b^2}+\frac{y^2}{a^2} = 1$ -
Now, differentiate w..r.t. x
$\frac{2x}{b^2}+\frac{2y}{a^2}.\frac{dy}{dx}=0\\$ -(i)
Now, again differentiate w.r.t. x
$\frac{2}{b^2}+\frac{2}{a^2}.y^{'}.y^{'}+\frac{2y}{a^2}.y^{''}=0\\ \\ \frac{1}{b^2}=-\frac{1}{a^2}\left ( (y^{'})^2+yy^{''} \right )$ -(ii)
Put value from equation (ii) in (i)
Our equation becomes
$\frac{2y}{a^2}y^{'}-\frac{2x}{a^2}\left ( (y^{'})^2+yy^{''} \right )=0\\ \\ 2yy^{'}-2(y^{'})^2x+2yy^{''}x=0\\ \\ xyy^{''}-x(y^{'})^2+yy^{'}= 0$
Therefore, the required equation is $xyy^{''}-x(y^{'})^2+yy^{'}= 0$

Question:9 Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.

Answer:

Equation of hyperbolas having foci on x-axis and centre at the origin
$\frac{x^2}{b^2}+\frac{y^2}{a^2} = 1$
Now, differentiate w..r.t. x
$\frac{2x}{b^2}+\frac{2y}{a^2}.\frac{dy}{dx}=0\\$ -(i)
Now, again differentiate w.r.t. x
$\frac{2}{b^2}+\frac{2}{a^2}.y^{'}.y^{'}+\frac{2y}{a^2}.y^{''}=0\\ \\ \frac{1}{b^2}=-\frac{1}{a^2}\left ( (y^{'})^2+yy^{''} \right )$ -(ii)
Put value from equation (ii) in (i)
Our equation becomes
$\frac{2y}{a^2}y^{'}-\frac{2x}{a^2}\left ( (y^{'})^2+yy^{''} \right )=0\\ \\ 2yy^{'}-2(y^{'})^2x+2yy^{''}x=0\\ \\ xyy^{''}-x(y^{'})^2+yy^{'}= 0$
Therefore, the required equation is $xyy^{''}-x(y^{'})^2+yy^{'}= 0$

Question:10 Form the differential equation of the family of circles having centre on y-axis and radius 3 units.

Answer:

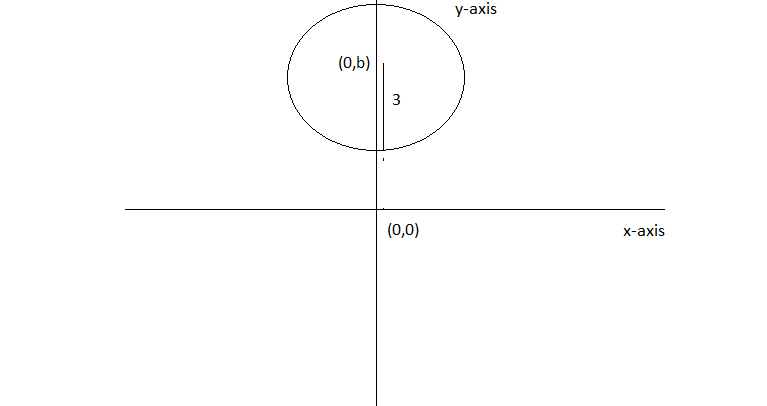1628484856150 Equation of the family of circles having centre on y-axis and radius 3 units
Let suppose centre is at (0,b)
Now, equation of circle with center (0,b) an radius = 3 units
$(x-0)^2+(y-b)^2=3^2 \ \ \ \ \ \ \ \ \ \ \ -(i)\\ x^2+y^2+b^2-2yb = 9$
Now, differentiate w.r.t x
we get,
$2x+2yy^{'}-2by^{'}= 0\\ 2x+2y(y-b)= 0\\ (y-b)=\frac{-x}{y^{'}} \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
Put value fro equation (ii) in (i)
$(x-0)^2+(\frac{-x}{y^{'}})^2=3^2 \\ x^2+\frac{x^2}{(y^{'})^2}=9\\ x^2(y^{'})^2+x^2=9(y^{'})^2\\ \\ (x^2-9)(y^{'})^2+x^2 = 0$
Therefore, the required differential equation is $(x^2-9)(y^{'})^2+x^2 = 0$

Question:11 Which of the following differential equations has $y = c_1e^x + c_2e^{-x}$ as the general solution?

(A) $\frac{d^2y}{dx^2} + y = 0$

(B) $\frac{d^2y}{dx^2} - y = 0$

(D) $\frac{d^2y}{dx^2} -1 = 0$

Answer:

Given general solution is
$y = c_1e^x + c_2e^{-x}$
Differentiate it w.r.t x
we will get
$\frac{dy}{dx} = c_1e^x-c_2e^{-x}$
Again, Differentiate it w.r.t x
$\frac{d^2y}{dx^2} = c_1e^x+c_2e^{x}=y\\ \frac{d^2y}{dx^2} - y = 0$
Therefore, (B) is the correct answer

Question:12 Which of the following differential equations has $y = x$ as one of its particular solution?

(A) $\frac{d^2y}{dx^2} - x^2\frac{dy}{dx} + xy =x$

(B) $\frac{d^2y}{dx^2} + x\frac{dy}{dx} + xy =x$

(D) $\frac{d^2y}{dx^2} + x\frac{dy}{dx} + xy =0$

Answer:

Given equation is
$y = x$
Now, on differentiating it w.r.t x
we get,
$\frac{dy}{dx} = 1$
and again on differentiating it w.r.t x
we get,

$\frac{d^2y}{dx^2} = 0$
Now, on substituting the values of $\frac{d^2y}{dx^2} , \frac{dy}{dx} \ and \ y$ in all the options we will find that only option c which is $\frac{d^2y}{dx^2} - x^2\frac{dy}{dx} + xy =0$ satisfies
Therefore, the correct answer is (C)

NCERT class 12 maths chapter 9 question answer - Exercise: 9.4

Question:1 Find the general solution: $\frac{dy}{dx} = \frac{1-\cos x}{1 + \cos x}$

Answer:

Given,

$\frac{dy}{dx} = \frac{1-\cos x}{1 + \cos x}$

$\\ \implies\frac{dy}{dx} = \frac{2sin^2\frac{x}{2}}{2cos^2\frac{x}{2}} = tan^2\frac{x}{2} \\ \implies dy = (sec^2\frac{x}{2} - 1)dx$

$\\ \implies \int dy = \int sec^2\frac{x}{2}dx - \int dx \\ \implies y = 2tan^{-1}\frac{x}{2} - x + C$

Question:2 Find the general solution: $\frac{dy}{dx} = \sqrt{4-y^2}\ (-2 < y < 2)$

Answer:

Given, in the question

$\frac{dy}{dx} = \sqrt{4-y^2}$

$\\ \implies \frac{dy}{\sqrt{4-y^2}} = dx \\ \implies \int \frac{dy}{\sqrt{4-y^2}} = \int dx$

$\\ (\int \frac{dy}{\sqrt{a^2-y^2}} = sin^{-1}\frac{y}{a})\\$

The required general solution:

$\\ \implies sin^{-1}\frac{y}{2} = x + C$

Question:3 Find the general solution: $\frac{dy}{dx} + y = 1 (y\neq 1)$

Answer:

Given, in the question

$\frac{dy}{dx} + y = 1$

$\\ \implies \frac{dy}{dx} = 1- y \\ \implies \int\frac{dy}{1-y} = \int dx$

$(\int\frac{dx}{x} = lnx)$

$\\ \implies -log(1-y) = x + C\ \ (We\ can\ write\ C= log k) \\ \implies log k(1-y) = -x \\ \implies 1- y = \frac{1}{k}e^{-x} \\$

The required general equation

$\implies y = 1 -\frac{1}{k}e^{-x}$

Question:4 Find the general solution: $\sec^2 x \tan y dx + \sec^2 y \tan x dy = 0$

Answer:

Given,

$\sec^2 x \tan y dx + \sec^2 y \tan x dy = 0$

$\\ \implies \frac{sec^2 y}{tan y}dy = -\frac{sec^2 x}{tan x}dx \\ \implies \int \frac{sec^2 y}{tan y}dy = - \int \frac{sec^2 x}{tan x}dx$

Now, let tany = t and tanx = u

$sec^2 y dy = dt\ and\ sec^2 x dx = du$

$\\ \implies \int \frac{dt}{t} = -\int \frac{du}{u} \\ \implies log t = -log u +logk \\ \implies t = \frac{1}{ku} \\ \implies tany = \frac{1}{ktanx}$

Question:5 Find the general solution:

$(e^x + e^{-x})dy - (e^x - e^{-x})dx = 0$

Answer:

Given, in the question

$(e^x + e^{-x})dy - (e^x - e^{-x})dx = 0$

$\\ \implies dy = \frac{(e^x - e^{-x})}{(e^x + e^{-x})}dx$

Let,

$\\ (e^x + e^{-x}) = t \\ \implies (e^x - e^{-x})dx = dt$

$\\ \implies \int dy = \int \frac{dt}{t} \\ \implies y = log t + C \\ \implies y = log(e^x + e^{-x}) + C$

This is the general solution

Question:6 Find the general solution: $\frac{dy}{dx} = (1+x^2)(1+y^2)$

Answer:

Given, in the question

$\frac{dy}{dx} = (1+x^2)(1+y^2)$

$\\ \implies \int \frac{dy}{(1+y^2)} = \int (1+x^2)dx$

$(\int \frac{dx}{(1+x^2)} =tan^{-1}x +c)$

$\\ \implies tan^{-1}y = x+\frac{x^3}{3} + C$

Question:7 Find the general solution: $y\log y dx - x dy = 0$

Answer:

Given,

$y\log y dx - x dy = 0$

$\\ \implies \frac{1}{ylog y}dy = \frac{1}{x}dx$

let logy = t

=> 1/ydy = dt

$\\ \implies \int \frac{dt}{t} = \int \frac{1}{x}dx \\ \implies \log t = \log x + \log k \\ \implies t = kx \\ \implies \log y = kx$

This is the general solution

Question:8 Find the general solution: $x^5\frac{dy}{dx} = - y^5$

Answer:

Given, in the question

$x^5\frac{dy}{dx} = - y^5$

$\\ \implies \int \frac{dy}{y^5} = - \int \frac{dx}{x^5} \\ \implies \frac{y^{-4}}{-4} = -\frac{x^{-4}}{-4} + C \\ \implies \frac{1}{y^4} + \frac{1}{x^4} = C$

This is the required general equation.

Question:9 Find the general solution: $\frac{dy}{dx} = \sin^{-1}x$

Answer:

Given, in the question

$\frac{dy}{dx} = \sin^{-1}x$

$\implies \int dy = \int \sin^{-1}xdx$

Now,

$\int (u.v)dx = u\int vdx - \int(\frac{du}{dx}.\int vdx)dx$

Here, u = $\sin^{-1}x$ and v = 1

$\implies y = \sin^{-1}x .x - \int(\frac{1}{\sqrt{1-x^2}}.x)dx$

$\\ Let\ 1- x^2 = t \\ \implies -2xdx = dt \implies xdx = -dt/2$

$\\ \implies y = x\sin^{-1}x+ \int(\frac{dt}{2\sqrt{t}}) \\ \implies y = x\sin^{-1}x + \frac{1}{2}.2\sqrt{t} + C \\ \implies y = x\sin^{-1}x + \sqrt{1-x^2} + C$

Question:10 Find the general solution $e^x\tan y dx + (1-e^x)\sec^2 y dy = 0$

Answer:

Given,

$e^x\tan y dx + (1-e^x)\sec^2 y dy = 0$

$\\ \implies e^x\tan y dx = - (1-e^x)\sec^2 y dy \\ \implies \int \frac{\sec^2 y }{\tan y}dy = -\int \frac{e^x }{(1-e^x)}dx$

$\\ let\ tany = t \ and \ 1-e^x = u \\ \implies \sec^2 ydy = dt\ and \ -e^xdx = du$

$\\ \therefore \int \frac{dt }{t} = \int \frac{du }{u} \\ \implies \log t = \log u + \log k \\ \implies t = ku \\ \implies \tan y= k (1-e^x)$

Question:11 Find a particular solution satisfying the given condition:

$(x^3 + x^2 + x + 1)\frac{dy}{dx} = 2x^2 + x; \ y = 1\ \textup{when}\ x = 0$

Answer:

Given, in the question

$(x^3 + x^2 + x + 1)\frac{dy}{dx} = 2x^2 + x$

$\\ \implies \int dy = \int\frac{2x^2 + x}{(x^3 + x^2 + x + 1)}dx$

$(x^3 + x^2 + x + 1) = (x +1)(x^2+1)$

Now,

Now comparing the coefficients

A + B = 2; B + C = 1; A + C = 0

Solving these:

Putting the values of A,B,C:

Therefore,

Now, y= 1 when x = 0

c = 1

Putting the value of c, we get:

Question:12 Find a particular solution satisfying the given condition:

$x(x^2 -1)\frac{dy}{dx} =1;\ y = 0\ \textup{when} \ x = 2$

Answer:

Given, in the question

$x(x^2 -1)\frac{dy}{dx} =1$

$\\ \implies \int dy=\int \frac{dx}{x(x^2 -1)} \\ \implies \int dy=\int \frac{dx}{x(x -1)(x+1)}$

Let,

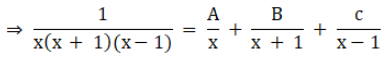
1628485409903

Now comparing the values of A,B,C

A + B + C = 0; B-C = 0; A = -1

Solving these:

Now putting the values of A,B,C

1517900488152880

Given, y =0 when x =2

1517900489745379

Therefore,

$\\ \implies y = \frac{1}{2}\log[\frac{4(x-1)(x+1)}{3x^2}]$

$\\ \implies y = \frac{1}{2}\log[\frac{4(x^2-1)}{3x^2}]$

Question:13 Find a particular solution satisfying the given condition:

$\cos\left(\frac{dy}{dx} \right ) = a\ (a\in R);\ y = 1\ \textup{when}\ x = 0$

Answer:

Given,

$\cos\left(\frac{dy}{dx} \right ) = a$

$\\ \implies \frac{dy}{dx} = \cos^{-1}a \\ \implies \int dy = \int\cos^{-1}a\ dx \\ \implies y = x\cos^{-1}a + c$

Now, y =1 when x =0

1 = 0 + c

Therefore, c = 1

Putting the value of c:

$\implies y = x\cos^{-1}a + 1$

Question:14 Find a particular solution satisfying the given condition:

$\frac{dy}{dx} = y\tan x; \ y =1\ \textup{when}\ x = 0$

Answer:

Given,

$\frac{dy}{dx} = y\tan x$

$\\ \implies \int \frac{dy}{y} = \int \tan x\ dx \\ \implies \log y = \log \sec x + \log k \\ \implies y = k\sec x$

Now, y=1 when x =0

1 = ksec0

$\implies$ k = 1

Putting the vlue of k:

y = sec x

Question:15 Find the equation of a curve passing through the point (0, 0) and whose differential equation is $y' = e^x\sin x$ .

Answer:

We first find the general solution of the given differential equation

Given,

$y' = e^x\sin x$

$\\ \implies \int dy = \int e^x\sin xdx$

$\\ Let I = \int e^x\sin xdx \\ \implies I = \sin x.e^x - \int(\cos x. e^x)dx \\ \implies I = e^x\sin x - [e^x\cos x - \int(-\sin x.e^x)dx] \\ \implies 2I = e^x(\sin x - \cos x) \\ \implies I = \frac{1}{2}e^x(\sin x - \cos x)$

$\\ \therefore y = \frac{1}{2}e^x(\sin x - \cos x) + c$

Now, Since the curve passes through (0,0)

y = 0 when x =0

$\\ \therefore 0 = \frac{1}{2}e^0(\sin 0 - \cos 0) + c \\ \implies c = \frac{1}{2}$

Putting the value of c, we get:

$\\ \therefore y = \frac{1}{2}e^x(\sin x - \cos x) + \frac{1}{2} \\ \implies 2y -1 = e^x(\sin x - \cos x)$

Question:16 For the differential equation $xy\frac{dy}{dx} = (x+2)(y+2)$ , find the solution curve passing through the point (1, –1).

Answer:

We first find the general solution of the given differential equation

Given,

$xy\frac{dy}{dx} = (x+2)(y+2)$

$\\ \implies \int \frac{y}{y+2}dy = \int \frac{x+2}{x}dx \\ \implies \int \frac{(y+2)-2}{y+2}dy = \int (1 + \frac{2}{x})dx \\ \implies \int (1 - \frac{2}{y+2})dy = \int (1 + \frac{2}{x})dx \\ \implies y - 2\log (y+2) = x + 2\log x + C$

Now, Since the curve passes through (1,-1)

y = -1 when x = 1

$\\ \therefore -1 - 2\log (-1+2) = 1 + 2\log 1 + C \\ \implies -1 -0 = 1 + 0 +C \\ \implies C = -2$

Putting the value of C:

$\\ y - 2\log (y+2) = x + 2\log x + -2 \\ \implies y -x + 2 = 2\log x(y+2)$

Question:17 Find the equation of a curve passing through the point $( 0 ,-2)$ given that at any point $(x,y)$ on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.

Answer:

According to the question,

$y\frac{dy}{dx} =x$

$\\ \implies \int ydy =\int xdx \\ \implies \frac{y^2}{2} = \frac{x^2}{2} + c$

Now, Since the curve passes through (0,-2).

x =0 and y = -2

$\\ \implies \frac{(-2)^2}{2} = \frac{0^2}{2} + c \\ \implies c = 2$

Putting the value of c, we get

$\\ \frac{y^2}{2} = \frac{x^2}{2} + 2 \\ \implies y^2 = x^2 + 4$

Question:18 At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).

Answer:

Slope m of line joining (x,y) and (-4,-3) is $\frac{y+3}{x+4}$

According to the question,

$\\ \frac{dy}{dx} = 2(\frac{y+3}{x+4}) \\ \implies \int \frac{dy}{y+3} = 2\int \frac{dx}{x+4} \\ \implies \log (y+3) = 2\log (x+4) + \log k \\ \implies (y+3) = k(x+4)^2$

Now, Since the curve passes through (-2,1)

x = -2 , y =1

$\\ \implies (1+3) = k(-2+4)^2 \\ \implies k =1$

Putting the value of k, we get

$\\ \implies y+3 = (x+4)^2$

Question:19 The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.

Answer:

Volume of a sphere, $V = \frac{4}{3}\pi r ^3$

Given, Rate of change is constant.

$\\ \therefore \frac{dV}{dt} = c \\ \implies \frac{d}{dt} (\frac{4}{3}\pi r ^3) = c \\ \implies \int d(\frac{4}{3}\pi r ^3) = c\int dt \\ \implies \frac{4}{3}\pi r ^3 = ct + k$

Now, at t=0, r=3 and at t=3 , r =6

Putting these value:

$\frac{4}{3}\pi (3) ^3 = c(0) + k \\ \implies k = 36\pi$

Also,

$\frac{4}{3}\pi (6) ^3 = c(3) + 36\pi \\ \implies 3c = 252\pi \\ \implies c = 84\pi$

Putting the value of c and k:

$\\ \frac{4}{3}\pi r ^3 = 84\pi t + 36\pi \\ \implies r ^3 = (21 t + 9)(3) = 62t + 27 \\ \implies r = \sqrt[3]{62t + 27}$

Question:20 In a bank, principal increases continuously at the rate of r % per year. Find the value of r if Rs 100 double itself in 10 years (log _e 2 = 0.6931).

Answer:

Let p be the principal amount and t be the time.

According to question,

$\frac{dp}{dt} = (\frac{r}{100})p$

$\\ \implies \int\frac{dp}{p} = \int (\frac{r}{100})dt \\ \implies \log p = \frac{r}{100}t + C$

$\\ \implies p = e^{\frac{rt}{100} + C}$

Now, at t =0 , p = 100

and at t =10, p = 200

Putting these values,

$\\ \implies 100 = e^{\frac{r(0)}{100} + C} = e^C$

Also,

, $\\ \implies 200 = e^{\frac{r(10)}{100} + C} = e^{\frac{r}{10}}.e^C = e^{\frac{r}{10}}.100 \\ \implies e^{\frac{r}{10}} = 2 \\ \implies \frac{r}{10} = \ln 2 = 0.6931 \\ \implies r = 6.93$

So value of r = 6.93%

Question:21 In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years (e ^0.5 = 1.648).

Answer:

Let p be the principal amount and t be the time.

According to question,

$\frac{dp}{dt} = (\frac{5}{100})p$

$\\ \implies \int\frac{dp}{p} = \int (\frac{1}{20})dt \\ \implies \log p = \frac{1}{20}t + C$

$\\ \implies p = e^{\frac{t}{20} + C}$

Now, at t =0 , p = 1000

Putting these values,

$\\ \implies 1000 = e^{\frac{(0)}{20} + C} = e^C$

Also, At t=10

, $\\ \implies p = e^{\frac{(10)}{20} + C} = e^{\frac{1}{2}}.e^C = e^{\frac{1}{2}}.1000 \\ \implies p =(1.648)(1000) = 1648$

After 10 years, the total amount would be Rs.1648

Question:22 In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?

Answer:

Let n be the number of bacteria at any time t.

According to question,

$\frac{dn}{dt} = kn\ \ (k\ is\ a\ constant)$

$\\ \implies \int \frac{dn}{n} = \int kdt \\ \implies \log n = kt + C$

Now, at t=0, n = 100000

$\\ \implies \log (100000) = k(0) + C \\ \implies C = 5$

Again, at t=2, n= 110000

$\\ \implies \log (110000) = k(2) + 5 \\ \implies \log 11 + 4 = 2k + 5 \\ \implies 2k = \log 11 -1 =\log \frac{11}{10} \\ \implies k = \frac{1}{2}\log \frac{11}{10}$

Using these values, for n= 200000

$\\ \implies \log (200000) = kt + C \\ \implies \log 2 +5 = kt + 5 \\ \implies (\frac{1}{2}\log \frac{11}{10})t = \log 2 \\ \implies t = \frac{2\log 2}{ \log \frac{11}{10}}$

Question:23 The general solution of the differential equation $\frac{dy}{dx} = e^{x+y}$ is

(A) $e^x + e^{-y} = C$

(B) $e^{x }+ e^{y} = C$

(D) $e^{-x }+ e^{-y} = C$

Answer:

Given,

$\frac{dy}{dx} = e^{x+y}$

$\\ \implies\frac{dy}{dx} = e^x.e^y \\ \implies\int \frac{dy}{e^y} = \int e^x.dx \\ \implies -e^{-y} = e^x + C \\ \implies e^x + e^{-y} = K\ \ \ \ (Option A)$

NCERT class 12 maths chapter 9 question answer - Exercise: 9.5

Question:1 Show that the given differential equation is homogeneous and solve each of them. $(x^2 + xy)dy = (x^2 + y^2)dx$

Answer:

The given diffrential eq can be written as
$\frac{dy}{dx}=\frac{x^{2}+y^{2}}{x^{2}+xy}$
Let $F(x,y)=\frac{x^{2}+y^{2}}{x^{2}+xy}$
Now, $F(\lambda x,\lambda y)=\frac{(\lambda x)^{2}+(\lambda y)^{2}}{(\lambda x)^{2}+(\lambda x)(\lambda y)}$
$=\frac{x^{2}+y^{2}}{x^{2}+xy} = \lambda ^{0}F(x,y)$ Hence, it is a homogeneous equation.

To solve it put y = vx
Diff erentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\v +x\frac{dv}{dx} = \frac{x^{2}+(vx)^{2}}{x^{2}+x(vx)}\\ v +x\frac{dv}{dx} = \frac{1+v^{2}}{1+v}$

$x\frac{dv}{dx} = \frac{(1+v^{2})-v(1+v)}{1+v} = \frac{1-v}{1+v}$

$( \frac{1+v}{1-v})dv = \frac{dx}{x}$

$( \frac{2}{1-v}-1)dv = \frac{dx}{x}$
Integrating on both side, we get;
$\\-2\log(1-v)-v=\log x -\log k\\ v= -2\log (1-v)-\log x+\log k\\ v= \log\frac{k}{x(1-v)^{2}}\\$
Again substitute the value $y = \frac{v}{x}$ ,we get;

$\\\frac{y}{x}= \log\frac{kx}{(x-y)^{2}}\\ \frac{kx}{(x-y)^{2}}=e^{y/x}\\ (x-y)^{2}=kxe^{-y/x}$
This is the required solution of given diff. equation

Question:2 Show that the given differential equation is homogeneousand solve each of them. $y' = \frac{x+y}{x}$

Answer:

the above differential eq can be written as,

$\frac{dy}{dx} = F(x,y)=\frac{x+y}{x}$ ............................(i)

Now, $F(\lambda x,\lambda y)=\frac{\lambda x+\lambda y}{\lambda x} = \lambda ^{0}F(x,y)$
Thus the given differential eq is a homogeneous equaion
Now, to solve substitute y = vx
Diff erentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$v+x\frac{dv}{dx}= \frac{x+vx}{x} = 1+v$
$\\x\frac{dv}{dx}= 1\\ dv = \frac{dx}{x}$
Integrating on both sides, we get; (and substitute the value of $v =\frac{y}{x}$ )

$\\v =\log x+C\\ \frac{y}{x}=\log x+C\\ y = x\log x +Cx$
this is the required solution

Question:3 Show that the given differential equation is homogeneous and solve each of them.

$(x-y)dy - (x+y)dx = 0$

Answer:

The given differential eq can be written as;

$\frac{dy}{dx}=\frac{x+y}{x-y} = F(x,y)(let\ say)$ ....................................(i)

$F(\lambda x,\lambda y)=\frac{\lambda x+\lambda y}{\lambda x-\lambda y}= \lambda ^{0}F(x,y)$
Hence it is a homogeneous equation.

Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\v+x\frac{dv}{dx}= \frac{1+v}{1-v}\\ x\frac{dv}{dx} = \frac{1+v}{1-v}-v =\frac{1+v^{2}}{1-v}$

$\frac{1-v}{1+v^{2}}dv = (\frac{1}{1+v^{2}}-\frac{v}{1-v^{2}})dv=\frac{dx}{x}$
Integrating on both sides, we get;

$\tan^{-1}v-1/2 \log(1+v^{2})=\log x+C$
again substitute the value of $v=y/x$
$\\\tan^{-1}(y/x)-1/2 \log(1+(y/x)^{2})=\log x+C\\ \tan^{-1}(y/x)-1/2 [\log(x^{2}+y^{2})-\log x^{2}]=\log x+C\\ tan^{-1}(y/x) = 1/2[\log (x^{2}+y^{2})]+C$

This is the required solution.

Question:4 Show that the given differential equation is homogeneous and solve each of them.

$(x^2 - y^2)dx + 2xydy = 0$

Answer:

we can write it as;

$\frac{dy}{dx}= -\frac{(x^{2}-y^{2})}{2xy} = F(x,y)\ (let\ say)$ ...................................(i)

$F(\lambda x,\lambda y) = \frac{(\lambda x)^{2}-(\lambda y)^{2}}{2(\lambda x)(\lambda y)} = \lambda ^{0}.F(x,y)$
Hence it is a homogeneous equation

Now, to solve substitute y = vx
Diff erentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$v+x\frac{dv}{dx} = \frac{ x^{2}-(vx)^{2}}{2x(vx)} =\frac{v^{2}-1}{2v}$
$\\x\frac{dv}{dx} =\frac{v^{2}+1}{2v}\\ \frac{2v}{1+v^{2}}dv=\frac{dx}{x}$
integrating on both sides, we get

$\log (1+v^{2})= -\log x +\log C = \log C/x$
$\\= 1+v^{2} = C/x\\ = x^2+y^{2}=Cx$ .............[ $v =y/x$ ]
This is the required solution.

Question:5 Show that the given differential equation is homogeneous and solve it.

$x^2\frac{dy}{dx} = x^2 - 2y^2 +xy$

Answer:

$\frac{dy}{dx}= \frac{x^{2}-2y^{2}+xy}{x^{2}} = F(x,y)\ (let\ say)$

$F(\lambda x,\lambda y)= \frac{(\lambda x)^{2}-2(\lambda y)^{2}+(\lambda .\lambda )xy}{(\lambda x)^{2}} = \lambda ^{0}.F(x,y)$ ............(i)
Hence it is a homogeneous eq

Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\v+x\frac{dv}{dx}= 1-2v^{2}+v\\ x\frac{dv}{dx} = 1-2v^{2}\\ \frac{dv}{1-2v^{2}}=\frac{dx}{x}$

$1/2[\frac{dv}{(1/\sqrt{2})^{2}-v^{2}}] = \frac{dx}{x}$

On integrating both sides, we get;

$\frac{1}{2\sqrt{2}}\log (\frac{1/\sqrt{2}+v}{1/\sqrt{2}-v}) = \log x +C$
after substituting the value of $v= y/x$

$\frac{1}{2\sqrt{2}}\log (\frac{x+\sqrt{2}y}{x-\sqrt{2}y}) = \log \left | x \right | +C$

This is the required solution

Question:6 Show that the given differential equation is homogeneous and solve it.

$xdy - ydx = \sqrt{x^2 + y^2}dx$

Answer:

$\frac{dy}{dx}=\frac{y+\sqrt{x^{2}+y^{2}}}{x} = F(x,y)$ .................................(i)

$F(\mu x,\mu y)=\frac{\mu y+\sqrt{(\mu x)^{2}+(\mu y)^{2}}}{\mu x} =\mu^{0}.F(x,y)$
henxe it is a homogeneous equation

Now, to solve substitute y = vx

Diff erentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$v+x\frac{dv}{dx}= v+\sqrt{1+v^{2}}=\sqrt{1+v^{2}}$

$=\frac{dv}{\sqrt{1+v^{2}}} =\frac{dx}{x}$

On integrating both sides,

$\Rightarrow \log \left | v+\sqrt{1+v^{2}} \right | = \log \left | x \right |+\log C$
Substitute the value of v=y/x , we get

$\\\Rightarrow \log \left | \frac{y+\sqrt{x^{2}+y^{2}}}{x} \right | = \log \left | Cx \right |\\ y+\sqrt{x^{2}+y^{2}} = Cx^{2}$

Required solution

Question:7 Solve.

$\left\{x\cos\left(\frac{y}{x} \right ) + y\sin\left(\frac{y}{x} \right ) \right \}ydx = \left\{y\sin\left(\frac{y}{x} \right ) - x\cos\left(\frac{y}{x} \right ) \right \}xdy$

Answer:

$\frac{dy}{dx} =\frac{x \cos(y/x)+y\sin(y/x)}{y\sin(y/x)-x\cos(y/x)}.\frac{y}{x} = F(x,y)$ ......................(i)
By looking at the equation we can directly say that it is a homogenous equation.

Now, to solve substitute y = vx

Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\=v+x\frac{dv}{dx} =\frac{v \cos v+v^{2}\sin v}{v\sin v-\cos v}\\ =x\frac{dv}{dx} = \frac{2v\cos v}{v\sin v-\cos v}\\ =(\tan v-1/v)dv = \frac{2dx}{x}$

integrating on both sides, we get

$\\=\log(\frac{\sec v}{v})= \log (Cx^{2})\\=\sec v/v =Cx^{2}$
substitute the value of v= y/x , we get

$\\\sec(y/x) =Cxy \\ xy \cos (y/x) = k$

Required solution

Question:8 Solve.

$x\frac{dy}{dx} - y + x\sin\left(\frac{y}{x}\right ) = 0$

Answer:

$\frac{dy}{dx}=\frac{y-x \sin(y/x)}{x} = F(x,y)$ ...............................(i)

$F(\mu x, \mu y)=\frac{\mu y-\mu x \sin(\mu y/\mu x)}{\mu x} = \mu^{0}.F(x,y)$
it is a homogeneous equation

Now, to solve substitute y = vx

Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$v+x\frac{dv}{dx}= v- \sin v = -\sin v$
$\Rightarrow -\frac{dv}{\sin v} = -(cosec\ v)dv=\frac{dx}{x}$

On integrating both sides we get;

$\\\Rightarrow \log \left | cosec\ v-\cot v \right |=-\log x+ \log C\\ \Rightarrow cosec (y/x) - \cot (y/x) = C/x$

$= x[1-\cos (y/x)] = C \sin (y/x)$ Required solution

Question:9 Solve.

$ydx + x\log\left(\frac{y}{x} \right ) -2xdy = 0$

Answer:

$\frac{dy}{dx}= \frac{y}{2x-x \log(y/x)} = F(x,y)$ ..................(i)

$\frac{\mu y}{2\mu x-\mu x \log(\mu y/\mu x)} = F(\mu x,\mu y) = \mu^{0}.F(x,y)$

hence it is a homogeneous eq

Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\=v+x\frac{dv}{dx}= \frac{v}{2-\log v}\\ =x\frac{dv}{dx} = \frac{v\log v-v}{2-\log v}\\ =[\frac{1}{v(\log v-1)}-\frac{1}{v}]dv=\frac{dx}{x}$
integrating on both sides, we get; ( substituting v =y/x)

$\\\Rightarrow \log[\log(y/x)-1]-\log(y/x)=\log(Cx)\\\Rightarrow \frac{x}{y}[\log(y/x)-1]=Cx\\ \Rightarrow \log (y/x)-1=Cy$

This is the required solution of the given differential eq

Question:10 Solve.

$\left(1 + e^{\frac{x}{y}} \right )dx + e^\frac{x}{y}\left(1-\frac{x}{y}\right )dy = 0$

Answer:

$\frac{dx}{dy}=\frac{-e^{x/y}(1-x/y)}{1+e^{x/y}} = F(x,y)$ .......................................(i)

$= F(\mu x,\mu y)=\frac{-e^{\mu x/\mu y}(1-\mu x/\mu y)}{1+e^{\mu x/\mu y}} =\mu^{0}.F(x,y)$
Hence it is a homogeneous equation.

Now, to solve substitute x = yv

Diff erentiating on both sides wrt $x$
$\frac{dx}{dy}= v +y\frac{dv}{dy}$

Substitute this value in equation (i)

$\\=v+y\frac{dv}{dy} = \frac{-e^{v}(1-v)}{1+e^{v}} \\ =y\frac{dv}{dy} = -\frac{v+e^{v}}{1+e^{v}}\\ =\frac{1+e^{v}}{v+e^{v}}dv=-\frac{dy}{y}$

Integrating on both sides, we get;

$\dpi{100} \log(v+e^{v})=-\log y+ \log c =\log (c/y)\\ =[\frac{x}{y}+e^{x/y}]= \frac{c}{y}\\\Rightarrow x+ye^{x/y}=c$
This is the required solution of the diff equation.

Question:11 Solve for particular solution.

$(x + y)dy + (x -y)dx = 0;\ y =1\ when \ x =1$

Answer:

$\frac{dy}{dx}=\frac{-(x-y)}{x+y} =F(x,y)$ ..........................(i)

We can clearly say that it is a homogeneous equation.

Now, to solve substitute y = vx

Diff erentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\v+x\frac{dv}{dx}=\frac{v-1}{v+1}\\ \Rightarrow x\frac{dv}{dx} = -\frac{(1+v^{2})}{1+v}$

$\frac{1+v}{1+v^{2}}dv = [\frac{v}{1+v^{2}}+\frac{1}{1+v^{2}}]dv=-\frac{dx}{x}$

On integrating both sides

$\\=\frac{1}{2}[\log (1+v^{2})]+\tan^{-1}v = -\log x +k\\ =\log(1+v^{2})+2\tan^{-1}v=-2\log x +2k\\ =\log[(1+(y/x)^{2}).x^{2}]+2\tan^{-1}(y/x)=2k\\ =\log(x^{2}+y^{2})+2\tan^{-1}(y/x) = 2k$ ......................(ii)

Now, y=1 and x= 1

$\\=\log 2 +2\tan^{-1}1=2k\\ =\pi/2+\log 2 = 2k\\$

After substituting the value of 2k in eq. (ii)

$\log(x^{2}+y^2)+2\tan^{-1}(y/x)=\pi/2+\log 2$

This is the required solution.

Question:12 Solve for particular solution.

$x^2dy + (xy + y^2)dx = 0; y =1\ \textup{when}\ x = 1$

Answer:

$\frac{dy}{dx}= \frac{-(xy+y^{2})}{x^{2}} = F(x,y)$ ...............................(i)

$F(\mu x, \mu y)=\frac{-\mu^{2}(xy+(\mu y)^{2})}{(\mu x)^{2}} =\mu ^{0}. F(x,y)$
Hence it is a homogeneous equation

Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i), we get

$\\=v+\frac{xdv}{dx}= -v- v^{2}\\ =\frac{xdv}{dx}=-v(v+2)\\ =\frac{dv}{v+2}=-\frac{dx}{x}\\ =1/2[\frac{1}{v}-\frac{1}{v+2}]dv=-\frac{dx}{x}$

Integrating on both sides, we get;

$\\=\frac{1}{2}[\log v -\log(v+2)]= -\log x+\log C\\ =\frac{v}{v+2}=(C/x)^{2}$

replace the value of v=y/x

$\frac{x^{2}y}{y+2x}=C^{2}$ .............................(ii)

Now y =1 and x = 1

$C = 1/\sqrt{3}$
therefore,

$\frac{x^{2}y}{y+2x}=1/3$

Required solution

Question:13 Solve for particular solution.

$\left [x\sin^2\left(\frac{y}{x} \right ) - y \right ]dx + xdy = 0;\ y =\frac{\pi}{4}\ when \ x = 1$

Answer:

$\frac{dy}{dx}=\frac{-[x\sin^{2}(y/x)-y]}{x} = F(x,y)$ ..................(i)

$F(\mu x,\mu y)=\frac{-[\mu x\sin^{2}(\mu y/\mu x)-\mu y]}{\mu x}=\mu ^{0}.F(x,y)$

Hence it is a homogeneous eq

Now, to solve substitute y = vx

Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

on integrating both sides, we get;

$\\-\cot v =\log\left | x \right | -C\\ =\cot v = \log\left | x \right |+\log C$

On substituting v =y/x

$=\cot (y/x) = \log\left | Cx \right |$ ............................(ii)

Now, $y = \pi/4\ @ x=1$

$\\\cot (\pi/4) = \log C \\ =C=e^{1}$

put this value of C in eq (ii)

$\cot (y/x)=\log\left | ex \right |$

Required solution.

Question:14 Solve for particular solution.

$\frac{dy}{dx} - \frac{y}{x} + \textup{cosec}\left (\frac{y}{x} \right ) = 0;\ y = 0 \ \textup{when}\ x = 1$

Answer:

$\frac{dy}{dx} = \frac{y}{x} -cosec(y/x) =F(x,y)$ ....................................(i)

the above eq is homogeneous. So,
Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\=v+x\frac{dv}{dx}=v- cosec\ v\\ =x\frac{dv}{dx} = -cosec\ v\\ =-\frac{dv}{cosec\ v}= \frac{dx}{x}\\ =-\sin v dv = \frac{dx}{x}$

on integrating both sides, we get;

$\\=cos\ v = \log x +\log C =\log Cx\\ =\cos(y/x)= \log Cx$ .................................(ii)

now y = 0 and x =1 , we get

$C =e^{1}$

put the value of C in eq 2

$\cos(y/x)=\log \left | ex \right |$

Question:15 Solve for particular solution.

$2xy + y^2 - 2x^2\frac{dy}{dx} = 0 ;\ y = 2\ \textup{when}\ x = 1$

Answer:

The above eq can be written as;

$\frac{dy}{dx}=\frac{2xy+y^{2}}{2x^{2}} = F(x,y)$
By looking, we can say that it is a homogeneous equation.

Now, to solve substitute y = vx
Differentiating on both sides wrt $x$
$\frac{dy}{dx}= v +x\frac{dv}{dx}$

Substitute this value in equation (i)

$\\=v+x\frac{dv}{dx}= \frac{2v+v^{2}}{2}\\ =x\frac{dv}{dx} = v^{2}/2\\ = \frac{2dv}{v^{2}}=\frac{dx}{x}$

integrating on both sides, we get;

$\\=-2/v=\log \left | x \right |+C\\ =-\frac{2x}{y}=\log \left | x \right |+C$ .............................(ii)

Now, y = 2 and x =1, we get

C =-1
put this value in equation(ii)

$\\=-\frac{2x}{y}=\log \left | x \right |-1\\ \Rightarrow y = \frac{2x}{1- \log x}$

Question:16 A homogeneous differential equation of the from $\frac{dx}{dy}= h\left(\frac{x}{y} \right )$ can be solved by making the substitution.

(A) $y = vx$

(B) $v = yx$

(D) $x =v$

Answer:

$\frac{dx}{dy}= h\left(\frac{x}{y} \right )$
for solving this type of equation put x/y = v
x = vy

option C is correct

Question:17 Which of the following is a homogeneous differential equation?

(A) $(4x + 6x +5)dy - (3y + 2x +4)dx = 0$

(B) $(xy)dx - (x^3 + y^3)dy = 0$

(D) $y^2dx + (x^2 -xy -y^2)dy = 0$

Answer:

Option D is the right answer.

$y^2dx + (x^2 -xy -y^2)dy = 0$
$\frac{dy}{dx}=\frac{y^{2}}{x^{2}-xy-y^{2}} = F(x,y)$
we can take out lambda as a common factor and it can be cancelled out

NCERT class 12 maths chapter 9 question answer - Exercise: 9.6

Question:1 Find the general solution:

$\frac{dy}{dx} + 2y = \sin x$

Answer:

Given equation is
$\frac{dy}{dx} + 2y = \sin x$
This is $\frac{dy}{dx} + py = Q$ type where p = 2 and Q = sin x
Now,
$I.F. = e^{\int pdx}= e^{\int 2dx}= e^{2x}$
Now, the solution of given differential equation is given by relation
$Y(I.F.) =\int (Q\times I.F.)dx +C$
$Y(e^{\int 2x }) =\int (\sin x\times e^{\int 2x })dx +C$
Let $I =\int (\sin x\times e^{\int 2x })$
$I = \sin x \int e^{2x}dx- \int \left ( \frac{d(\sin x)}{dx}.\int e^{2x}dx \right )dx\\ \\ I = \sin x.\frac{e^{2x}}{2}- \int \left ( \cos x.\frac{e^{2x}}{2} \right )\\ \\ I = \sin x. \frac{e^{2x}}{2}-\frac{1}{2}\left ( \cos x\int e^{2x}dx- \left ( \frac{d(\cos x)}{dx}.\int e^{2x}dx \right ) \right )dx\\ \\ I = \sin x\frac{e^{2x}}{2}-\frac{1}{2}\left ( \cos x.\frac{e^{2x}}{2}+ \int \left ( \sin x.\frac{e^{2x}}{2} \right ) \right )\\ \\ I = \sin x\frac{e^{2x}}{2}-\frac{1}{2}\left ( \cos x.\frac{e^{2x}}{2}+\frac{I}{2} \right ) \ \ \ \ \ \ \ \ \ \ \ (\because I = \int \sin xe^{2x})\\ \\ \frac{5I}{4}= \frac{e^{2x}}{4}\left ( 2\sin x-\cos x \right )\\ \\ I = \frac{e^{2x}}{5}\left ( 2\sin x-\cos x \right )$
Put the value of I in our equation
Now, our equation become
$Y.e^{x^2 }= \frac{e^{2x}}{5}\left (2 \sin x-\cos x \right )+C$
$Y= \frac{1}{5}\left (2 \sin x-\cos x \right )+C.e^{-2x}$
Therefore, the general solution is $Y= \frac{1}{5}\left (2 \sin x-\cos x \right )+C.e^{-2x}$

Question:2 Solve for general solution:

$\frac{dy}{dx} + 3y = e^{-2x}$

Answer:

Given equation is
$\frac{dy}{dx} + 3y = e^{-2x}$
This is $\frac{dy}{dx} + py = Q$ type where p = 3 and $Q = e^{-2x}$
Now,
$I.F. = e^{\int pdx}= e^{\int 3dx}= e^{3x}$
Now, the solution of given differential equation is given by the relation
$Y(I.F.) =\int (Q\times I.F.)dx +C$
$Y(e^{ 3x }) =\int (e^{-2x}\times e^{ 3x })dx +C$
$Y(e^{ 3x }) =\int (e^{x})dx +C\\ Y(e^{3x})= e^x+C\\ Y = e^{-2x}+Ce^{-3x}$
Therefore, the general solution is $Y = e^{-2x}+Ce^{-3x}$

Question:3 Find the general solution

$\frac{dy}{dx} + \frac{y}{x} = x^2$

Answer:

Given equation is
$\frac{dy}{dx} + \frac{y}{x} = x^2$
This is $\frac{dy}{dx} + py = Q$ type where $p = \frac{1}{x}$ and $Q = x^2$
Now,
$I.F. = e^{\int pdx}= e^{\int \frac{1}{x}dx}= e^{\log x}= x$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(x) =\int (x^2\times x)dx +C$
$y(x) =\int (x^3)dx +C\\ y.x= \frac{x^4}{4}+C\\$
Therefore, the general solution is $yx =\frac{x^4}{4}+C$

Question:4 Solve for General Solution.

$\frac{dy}{dx} + (\sec x)y = \tan x \ \left(0\leq x < \frac{\pi}{2} \right )$

Answer:

Given equation is
$\frac{dy}{dx} + (\sec x)y = \tan x \ \left(0\leq x < \frac{\pi}{2} \right )$
This is $\frac{dy}{dx} + py = Q$ type where $p = \sec x$ and $Q = \tan x$
Now,
$I.F. = e^{\int pdx}= e^{\int \sec xdx}= e^{\log |\sec x+ \tan x|}= \sec x+\tan x$ $(\because 0\leq x\leq \frac{\pi}{2} \sec x > 0,\tan x > 0)$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(\sec x+\tan x) =\int ((\sec x+\tan x)\times \tan x)dx +C$
$y(\sec x+ \tan x) =\int (\sec x\tan x+\tan^2 x)dx +C\\y(\sec x+ \tan x) =\sec x+\int (\sec^2x-1)dx +C\\ y(\sec x+ \tan x) = \sec x +\tan x - x+C$
Therefore, the general solution is $y(\sec x+ \tan x) = \sec x +\tan x - x+C$

Question:5 Find the general solution.

$\cos^2 x\frac{dy}{dx} + y = \tan x\left(0\leq x < \frac{\pi}{2} \right )$

Answer:

Given equation is
$\cos^2 x\frac{dy}{dx} + y = \tan x\left(0\leq x < \frac{\pi}{2} \right )$
we can rewrite it as
$\frac{dy}{dx}+\sec^2x y= \sec^2x\tan x$
This is $\frac{dy}{dx} + py = Q$ where $p = \sec ^2x$ and $Q =\sec^2x \tan x$
Now,
$I.F. = e^{\int pdx}= e^{\int \sec^2 xdx}= e^{\tan x}$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(e^{\tan x}) =\int ((\sec^2 x\tan x)\times e^{\tan x})dx +C$
$ye^{\tan x} =\int \sec^2 x\tan xe^{\tan x}dx+C\\$
take
$e^{\tan x } = t\\ \Rightarrow \sec^2x.e^{\tan x}dx = dt$
$\int t.\log t dt = \log t.\int tdt-\int \left ( \frac{d(\log t)}{dt}.\int tdt \right )dt \\ \\ \int t.\log t dt = \log t . \frac{t^2}{2}- \int (\frac{1}{t}.\frac{t^2}{2})dt\\ \\ \int t.\log t dt = \log t.\frac{t^2}{2}- \int \frac{t}{2}dt\\ \\ \int t.\log t dt = \log t.\frac{t^2}{2}- \frac{t^2}{4}\\ \\ \int t.\log t dt = \frac{t^2}{4}(2\log t -1)$
Now put again $t = e^{\tan x}$
$\int \sec^2x\tan xe^{\tan x}dx = \frac{e^{2\tan x}}{4}(2\tan x-1)$
Put this value in our equation

$ye^{\tan x} =\frac{e^{2\tan x}}{4}(2\tan x-1)+C\\ \\$
Therefore, the general solution is $y =\frac{e^{\tan x}}{4}(2\tan x-1)+Ce^{-\tan x }\\$

Question:6 Solve for General Solution.

$x\frac{dy}{dx} + 2y = x^2\log x$

Answer:

Given equation is
$x\frac{dy}{dx} + 2y = x^2\log x$
Wr can rewrite it as
$\frac{dy}{dx} +2.\frac{y}{x}= x\log x$
This is $\frac{dy}{dx} + py = Q$ type where $p = \frac{2}{x}$ and $Q = x\log x$
Now,
$I.F. = e^{\int pdx}= e^{\int \frac{2}{x}dx}= e^{2\log x}=e^{\log x^2} = x^2$ $(\because 0\leq x\leq \frac{\pi}{2} \sec x > 0,\tan x > 0)$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(x^2) =\int (x\log x\times x^2)dx +C$
$x^2y = \int x^3\log x+ C$
Let
$I = \int x^3\log x\\ \\ I = \log x\int x^3dx-\int \left ( \frac{d(\log x)}{dx}.\int x^3dx \right )dx\\ \\ I = \log x.\frac{x^4}{4}- \int \left ( \frac{1}{x}.\frac{x^4}{4} \right )dx\\ \\ I = \log x.\frac{x^4}{4}- \int \left ( \frac{x^3}{4} \right )dx\\ \\ I = \log x.\frac{x^4}{4}-\frac{x^4}{16}$
Put this value in our equation
$x^2y =\log x.\frac{x^4}{4}-\frac{x^4}{16}+ C\\ \\ y = \frac{x^2}{16}(4\log x-1)+C.x^{-2}$
Therefore, the general solution is $y = \frac{x^2}{16}(4\log x-1)+C.x^{-2}$

Question:7 Solve for general solutions.

$x\log x\frac{dy}{dx} + y = \frac{2}{x}\log x$

Answer:

Given equation is
$x\log x\frac{dy}{dx} + y = \frac{2}{x}\log x$
we can rewrite it as
$\frac{dy}{dx}+\frac{y}{x\log x}= \frac{2}{x^2}$
This is $\frac{dy}{dx} + py = Q$ type where $p = \frac{1}{x\log x}$ and $Q =\frac{2}{x^2}$
Now,
$I.F. = e^{\int pdx}= e^{\int \frac{1}{x\log x} dx}= e^{\log(\log x)} = \log x$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(\log x) =\int ((\frac{2}{x^2})\times \log x)dx +C$

take
$I=\int ((\frac{2}{x^2})\times \log x)dx$
$I = \log x.\int \frac{2}{x^2}dx-\int \left ( \frac{d(\log x)}{dt}.\int \frac{x^2}{2}dx \right )dx \\ \\ I= -\log x . \frac{2}{x}+ \int (\frac{1}{x}.\frac{2}{x})dx\\ \\ I = -\log x.\frac{2}{x}+ \int \frac{2}{x^2}dx\\ \\I = -\log x.\frac{2}{x}- \frac{2}{x}\\ \\$
Put this value in our equation

$y\log x =-\frac{2}{x}(\log x+1)+C\\ \\$
Therefore, the general solution is $y\log x =-\frac{2}{x}(\log x+1)+C\\ \\$

Question:8 Find the general solution.

$(1 + x^2)dy + 2xydx = \cot x dx\ (x\neq 0)$

Answer:

Given equation is
$(1 + x^2)dy + 2xydx = \cot x dx\ (x\neq 0)$
we can rewrite it as
$\frac{dy}{dx}+\frac{2xy}{(1+x^2)}= \frac{\cot x}{1+x^2}$
This is $\frac{dy}{dx} + py = Q$ type where $p = \frac{2x}{1+ x^2}$ and $Q =\frac{\cot x}{1+x^2}$
Now,
$I.F. = e^{\int pdx}= e^{\int \frac{2x}{1+ x^2} dx}= e^{\log(1+ x^2)} = 1+x^2$
Now, the solution of the given differential equation is given by the relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(1+x^2) =\int ((\frac{\cot x}{1+x^2})\times (1+ x^2))dx +C$
$y(1+x^2) =\int \cot x dx+C\\ \\ y(1+x^2)= \log |\sin x|+ C\\ \\ y = (1+x^2)^{-1}\log |\sin x|+C(1+x^2)^{-1}$
Therefore, the general solution is $y = (1+x^2)^{-1}\log |\sin x|+C(1+x^2)^{-1}$

Question:9 Solve for general solution.

$x\frac{dy}{dx} + y -x +xy \cot x = 0\ (x \neq 0)$

Answer:

Given equation is
$x\frac{dy}{dx} + y -x +xy \cot x = 0\ (x \neq 0)$
we can rewrite it as
$\frac{dy}{dx}+y.\left ( \frac{1}{x}+\cot x \right )= 1$
This is $\frac{dy}{dx} + py = Q$ type where $p =\left ( \frac{1}{x}+\cot x \right )$ and $Q =1$
Now,
$I.F. = e^{\int pdx}= e^{\int \left ( \frac{1}{x}+\cot x \right ) dx}= e^{\log x +\log |\sin x|} = x.\sin x$
Now, the solution of the given differential equation is given by the relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(x.\sin x) =\int 1\times x\sin xdx +C$
$y(x.\sin x) =\int x\sin xdx +C$
Lets take
$I=\int x\sin xdx \\ \\ I = x .\int \sin xdx-\int \left ( \frac{d(x)}{dx}.\int \sin xdx \right )dx\\ \\ I =- x.\cos x+ \int (\cos x)dx\\ \\ I = -x\cos x+\sin x$
Put this value in our equation
$y(x.\sin x)= -x\cos x+\sin x + C\\ y = -\cot x+\frac{1}{x}+\frac{C}{x\sin x}$
Therefore, the general solution is $y = -\cot x+\frac{1}{x}+\frac{C}{x\sin x}$

Question:10 Find the general solution.

$(x+y)\frac{dy}{dx} = 1$

Answer:

Given equation is
$(x+y)\frac{dy}{dx} = 1$
we can rewrite it as
$\frac{dy}{dx} = \frac{1}{x+y}\\ \\ x+ y =\frac{dx}{dy}\\ \\ \frac{dx}{dy}-x=y$
This is $\frac{dx}{dy} + px = Q$ type where $p =-1$ and $Q =y$
Now,
$I.F. = e^{\int pdy}= e^{\int -1 dy}= e^{-y}$
Now, the solution of given differential equation is given by relation
$x(I.F.) =\int (Q\times I.F.)dy +C$
$x(e^{-y}) =\int y\times e^{-y}dy +C$
$xe^{-y}= \int y.e^{-y}dy + C$
Lets take
$I=\int ye^{-y}dy \\ \\ I = y .\int e^{-y}dy-\int \left ( \frac{d(y)}{dy}.\int e^{-y}dy \right )dy\\ \\ I =- y.e^{-y}+ \int e^{-y}dy\\ \\ I = - ye^{-y}-e^{-y}$
Put this value in our equation
$x.e^{-y} = -e^{-y}(y+1)+C\\ x = -(y+1)+Ce^{y}\\ x+y+1=Ce^y$
Therefore, the general solution is $x+y+1=Ce^y$

Question:11 Solve for general solution.

$y dx + (x - y^2)dy = 0$

Answer:

Given equation is
$y dx + (x - y^2)dy = 0$
we can rewrite it as
$\frac{dx}{dy}+\frac{x}{y}=y$
This is $\frac{dx}{dy} + px = Q$ type where $p =\frac{1}{y}$ and $Q =y$
Now,
$I.F. = e^{\int pdy}= e^{\int \frac{1}{y} dy}= e^{\log y } = y$
Now, the solution of given differential equation is given by relation
$x(I.F.) =\int (Q\times I.F.)dy +C$
$x(y) =\int y\times ydy +C$
$xy= \int y^2dy + C$
$xy = \frac{y^3}{3}+C$
$x = \frac{y^2}{3}+\frac{C}{y}$
Therefore, the general solution is $x = \frac{y^2}{3}+\frac{C}{y}$

Question:12 Find the general solution.

$(x+3y^2)\frac{dy}{dx} = y\ (y > 0)$

Answer:

Given equation is
$(x+3y^2)\frac{dy}{dx} = y\ (y > 0)$
we can rewrite it as
$\frac{dx}{dy}-\frac{x}{y}= 3y$
This is $\frac{dx}{dy} + px = Q$ type where $p =\frac{-1}{y}$ and $Q =3y$
Now,
$I.F. = e^{\int pdy}= e^{\int \frac{-1}{y} dy}= e^{-\log y } =y^{-1}= \frac{1}{y}$
Now, the solution of given differential equation is given by relation
$x(I.F.) =\int (Q\times I.F.)dy +C$
$x(\frac{1}{y}) =\int 3y\times \frac{1}{y}dy +C$
$\frac{x}{y}= \int 3dy + C$
$\frac{x}{y}= 3y+ C$
$x = 3y^2+Cy$
Therefore, the general solution is $x = 3y^2+Cy$

Question:13 Solve for particular solution.

$\frac{dy}{dx} + 2y \tan x = \sin x; \ y = 0 \ when \ x =\frac{\pi}{3}$

Answer:

Given equation is
$\frac{dy}{dx} + 2y \tan x = \sin x; \ y = 0 \ when \ x =\frac{\pi}{3}$
This is $\frac{dy}{dx} + py = Q$ type where $p = 2\tan x$ and $Q = \sin x$
Now,
$I.F. = e^{\int pdx}= e^{\int 2\tan xdx}= e^{2\log |\sec x|}= \sec^2 x$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(\sec^2 x) =\int ((\sin x)\times \sec^2 x)dx +C$
$y(\sec^2 x) =\int (\sin \times \frac{1}{\cos x}\times \sec x)dx +C\\ \\ y(\sec^2 x) = \int \tan x\sec xdx+ C\\ \\ y.\sec^2 x= \sec x+C$
Now, by using boundary conditions we will find the value of C
It is given that y = 0 when $x= \frac{\pi}{3}$
at $x= \frac{\pi}{3}$
$0.\sec \frac{\pi}{3} = \sec \frac{\pi}{3}+C\\ \\ C = - 2$
Now,

$y.\sec^2 x= \sec x - 2\\ \frac{y}{\cos ^2x}= \frac{1}{\cos x}- 2\\ y = \cos x- 2\cos ^2 x$
Therefore, the particular solution is $y = \cos x- 2\cos ^2 x$

Question:14 Solve for particular solution.

$(1 + x^2)\frac{dy}{dx} + 2xy =\frac{1}{1 + x^2}; \ y = 0 \ when \ x = 1$

Answer:

Given equation is
$(1 + x^2)\frac{dy}{dx} + 2xy =\frac{1}{1 + x^2}; \ y = 0 \ when \ x = 1$
we can rewrite it as
$\frac{dy}{dx}+\frac{2xy}{1+x^2}=\frac{1}{(1+x^2)^2}$
This is $\frac{dy}{dx} + py = Q$ type where $p =\frac{2x}{1+x^2}$ and $Q = \frac{1}{(1+x^2)^2}$
Now,
$I.F. = e^{\int pdx}= e^{\int \frac{2x}{1+x^2}dx}= e^{\log |1+x^2|}= 1+x^2$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(1+ x^2) =\int (\frac{1}{(1+x^2)^2}\times (1+x^2))dx +C$
$y(1+x^2) =\int \frac{1}{(1+x^2)}dx +C\\ \\ y(1+x^2) = \tan^{-1}x+ C\\ \\$
Now, by using boundary conditions we will find the value of C
It is given that y = 0 when x = 1
at x = 1
$0.(1+1^2) = \tan^{-1}1+ C\\ \\ C =- \frac{\pi}{4}$
Now,
$y(1+x^2)= \tan^{-1}x- \frac{\pi}{4}$
Therefore, the particular solution is $y(1+x^2)= \tan^{-1}x- \frac{\pi}{4}$

Question:15 Find the particular solution.

$\frac{dy}{dx} - 3y \cot x = \sin 2x;\ y = 2\ when \ x = \frac{\pi}{2}$

Answer:

Given equation is
$\frac{dy}{dx} - 3y \cot x = \sin 2x;\ y = 2\ when \ x = \frac{\pi}{2}$
This is $\frac{dy}{dx} + py = Q$ type where $p =-3\cot x$ and $Q =\sin 2x$
Now,
$I.F. = e^{\int pdx}= e^{-3\cot xdx}= e^{-3\log|\sin x|}= \sin ^{-3}x= \frac{1}{\sin^3x}$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(\frac{1}{\sin^3 x}) =\int (\sin 2x\times\frac{1}{\sin^3 x})dx +C$
$\frac{y}{\sin^3 x} =\int (2\sin x\cos x\times\frac{1}{\sin^3 x})dx +C$
$\frac{y}{\sin^3 x} =\int (2\times \frac{\cos x}{\sin x}\times\frac{1}{\sin x})dx +C$
$\frac{y}{\sin^3 x} =\int (2\times\cot x\times cosec x)dx +C$
$\frac{y}{\sin^3 x} =-2cosec x +C$
Now, by using boundary conditions we will find the value of C
It is given that y = 2 when $x= \frac{\pi}{2}$
at $x= \frac{\pi}{2}$
$\frac{2}{\sin^3\frac{\pi}{2}} = -2cosec \frac{\pi}{2}+C\\ \\ 2 = -2 +C\\ C = 4$
Now,
$y= 4\sin^3 x-2\sin^2x\\$
Therefore, the particular solution is $y= 4\sin^3 x-2\sin^2x\\$

Question:16 Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.

Answer:

Let f(x , y) is the curve passing through origin
Then, the slope of tangent to the curve at point (x , y) is given by $\frac{dy}{dx}$
Now, it is given that
$\frac{dy}{dx} = y + x\\ \\ \frac{dy}{dx}-y=x$
It is $\frac{dy}{dx}+py=Q$ type of equation where $p = -1 \ and \ Q = x$
Now,
$I.F. = e^{\int pdx}= e^{\int -1dx }= e^{-x}$
Now,
$y(I.F.)= \int (Q \times I.F. )dx+ C$
$y(e^{-x})= \int (x \times e^{-x} )dx+ C$
Now, Let
$I= \int (x \times e^{-x} )dx \\ \\ I = x.\int e^{-x}dx-\int \left ( \frac{d(x)}{dx}.\int e^{-x}dx \right )dx\\ \\ I = -xe^{-x}+\int e^{-x}dx\\ \\ I = -xe^{-x}-e^{-x}\\ \\ I = -e^{-x}(x+1)$
Put this value in our equation
$ye^{-x}= -e^{-x}(x+1)+C$
Now, by using boundary conditions we will find the value of C
It is given that curve passing through origin i.e. (x , y) = (0 , 0)
$0.e^{-0}= -e^{-0}(0+1)+C\\ \\ C = 1$
Our final equation becomes
$ye^{-x}= -e^{-x}(x+1)+1\\ y+x+1=e^x$
Therefore, the required equation of the curve is $y+x+1=e^x$

Question:17 Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.

Answer:

Let f(x , y) is the curve passing through point (0 , 2)
Then, the slope of tangent to the curve at point (x , y) is given by $\frac{dy}{dx}$
Now, it is given that
$\frac{dy}{dx} +5= y + x \\ \\ \frac{dy}{dx}-y=x-5$
It is $\frac{dy}{dx}+py=Q$ type of equation where $p = -1 \ and \ Q = x- 5$
Now,
$I.F. = e^{\int pdx}= e^{\int -1dx }= e^{-x}$
Now,
$y(I.F.)= \int (Q \times I.F. )dx+ C$
$y(e^{-x})= \int ((x-5) \times e^{-x} )dx+ C$
Now, Let
$I= \int ((x-5) \times e^{-x} )dx \\ \\ I = (x-5).\int e^{-x}dx-\int \left ( \frac{d(x-5)}{dx}.\int e^{-x}dx \right )dx\\ \\ I = -(x-5)e^{-x}+\int e^{-x}dx\\ \\ I = -xe^{-x}-e^{-x}+5e^{-x}\\ \\ I = -e^{-x}(x-4)$
Put this value in our equation
$ye^{-x}= -e^{-x}(x-4)+C$
Now, by using boundary conditions we will find the value of C
It is given that curve passing through point (0 , 2)
$2.e^{-0}= -e^{-0}(0-4)+C\\ \\ C = -2$
Our final equation becomes
$ye^{-x}= -e^{-x}(x-4)-2\\ y=4-x-2e^x$
Therefore, the required equation of curve is $y=4-x-2e^x$

Question:18 The Integrating Factor of the differential equation $x\frac{dy}{dx} - y = 2x^2$ is

(A) $e^{-x}$

(B) $e^{-y}$

(D) $x$

Answer:

Given equation is
$x\frac{dy}{dx} - y = 2x^2$
we can rewrite it as
$\frac{dy}{dx}-\frac{y}{x}= 2x$
Now,
It is $\frac{dy}{dx}+py=Q$ type of equation where $p = \frac{-1}{x} \ and \ Q = 2x$
Now,
$I.F. = e^{\int pdx} = e^{\int \frac{-1}{x}dx}= e^{\int -\log x }= x^{-1}= \frac{1}{x}$
Therefore, the correct answer is (C)

Question:19 The Integrating Factor of the differential equation $(1 - y^2)\frac{dx}{dy} + yx = ay \ \ (-1<y<1)$ is

(A) $\frac{1}{{y^2 -1}}$

(B) $\frac{1}{\sqrt{y^2 -1}}$

(D) $\frac{1}{\sqrt{1 - y^2 }}$

Answer:

Given equation is
$(1 - y^2)\frac{dx}{dy} + yx = ay \ \ (-1<y<1)$
we can rewrite it as
$\frac{dx}{dy}+\frac{yx}{1-y^2}= \frac{ay}{1-y^2}$
It is $\frac{dx}{dy}+px= Q$ type of equation where $p = \frac{y}{1-y^2}\ and \ Q = \frac{ay}{1-y^2}$
Now,
$I.F. = e^{\int pdy}= e^{\int \frac{y}{1-y^2}dy}= e^{\frac{\log |1 - y^2|}{-2}}= (1-y^2)^{\frac{-1}{2}}= \frac{1}{\sqrt{1-y^2}}$
Therefore, the correct answer is (D)

Class 12 Maths Chapter 9 NCERT solutions - Miscellaneous Exercise

Question:1 Indicate Order and Degree.

(i) $\frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x$

Answer:

Given function is
$\frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x$
We can rewrite it as
$y''+5x(y')^2-6y = \log x$
Now, it is clear from the above that, the highest order derivative present in differential equation is $y''$

Therefore, the order of the given differential equation $\frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x$ is 2
Now, the given differential equation is a polynomial equation in its derivative y '' and y 'and power raised to y '' is 1
Therefore, it's degree is 1

Question:1 Indicate Order and Degree.

(ii) $\left(\frac{dy}{dx} \right )^3 - 4\left(\frac{dy}{dx} \right )^2 + 7y = \sin x$

Answer:

Given function is
$\left(\frac{dy}{dx} \right )^3 - 4\left(\frac{dy}{dx} \right )^2 + 7y = \sin x$
We can rewrite it as
$(y')^3-4(y')^2+7y=\sin x$
Now, it is clear from the above that, the highest order derivative present in differential equation is y'

Therefore, order of given differential equation is 1
Now, the given differential equation is a polynomial equation in it's dervatives y 'and power raised to y ' is 3
Therefore, it's degree is 3

Question:1 Indicate Order and Degree.

(iii) $\frac{d^4 y}{dx^4} - \sin\left(\frac{d^3y}{dx^3} \right ) = 0$

Answer:

Given function is
$\frac{d^4 y}{dx^4} - \sin\left(\frac{d^3y}{dx^3} \right ) = 0$
We can rewrite it as
$y''''-\sin y''' = 0$
Now, it is clear from the above that, the highest order derivative present in differential equation is y''''

Therefore, order of given differential equation is 4
Now, the given differential equation is not a polynomial equation in it's dervatives
Therefore, it's degree is not defined

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(i) $xy = ae^x + be^{-x} + x^2\qquad :\ x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} - xy +x^2 -2 =0$

Answer:

Given,

$xy = ae^x + be^{-x} + x^2$

Now, differentiating both sides w.r.t. x,

$x\frac{dy}{dx} + y = ae^x - be^{-x} + 2x$

Again, differentiating both sides w.r.t. x,

$\\ (x\frac{d^2y}{dx^2} + \frac{dy}{dx}) + \frac{dy}{dx} = ae^x + be^{-x} + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} = ae^x + be^{-x} + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} = xy -x^2 + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} - xy + x^2 + 2$

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(ii) $y = e^x(a\cos x + b \sin x )\qquad : \ \frac{d^2y}{dx^2} - 2\frac{dy}{dx} + 2y = 0$

Answer:

Given,

$y = e^x(a\cos x + b \sin x )$

Now, differentiating both sides w.r.t. x,

$\frac{dy}{dx} = e^x(-a\sin x + b \cos x ) + e^x(a\cos x + b \sin x ) =e^x(-a\sin x + b \cos x ) +y$

Again, differentiating both sides w.r.t. x,

$\\ \frac{d^2y}{dx^2} = e^x(-a\cos x - b \sin x ) + e^x(-a\sin x + b \cos x ) + \frac{dy}{dx} \\ = -y + (\frac{dy}{dx} -y) + \frac{dy}{dx} \\ \implies \frac{d^2y}{dx^2} - 2\frac{dy}{dx} + 2y = 0$

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(iii) $y= x\sin 3x \qquad : \ \frac{d^2y}{dx^2} + 9y - 6\cos 3x = 0$

Answer:

Given,

$y= x\sin 3x$

Now, differentiating both sides w.r.t. x,

$y= x\sin 3x \frac{dy}{dx} = x(3\cos 3x) + \sin 3x$

Again, differentiating both sides w.r.t. x,

$\\ \frac{d^2y}{dx^2} = 3x(-3\sin 3x) + 3\cos 3x + 3\cos 3x \\ = -9y + 6\cos 3x \\ \implies \frac{d^2y}{dx^2} + 9y - 6\cos 3x = 0$

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(iv) $x^2 = 2y^2\log y\qquad : \ (x^2 + y^2)\frac{dy}{dx} - xy = 0$

Answer:

Given,

$x^2 = 2y^2\log y$

Now, differentiating both sides w.r.t. x,

$\\ 2x = (2y^2.\frac{1}{y} + 2(2y)\log y)\frac{dy}{dx} = 2(y + 2y\log y)\frac{dy}{dx} \\ \implies \frac{dy}{dx} = \frac{x}{y(1+ 2\log y)}$

Putting $\frac{dy}{dx}\ and \ x^2$ values in LHS

$\\ (2y^2\log y + y^2)\frac{dy}{dx} - xy = y^2(2\log y + 1)\frac{x}{y(1+ 2\log y)} -xy \\ = xy - xy = 0 = RHS$

Therefore, the given function is the solution of the corresponding differential equation.

Question:3 Form the differential equation representing the family of curves given by $(x-a)^2 + 2y^2 = a^2$ , where a is an arbitrary constant.

Answer:

Given equation is
$(x-a)^2 + 2y^2 = a^2$
we can rewrite it as
$2y^2 = a^2-(x-a)^2$ -(i)
Differentiate both the sides w.r.t x
$\frac{d\left ( 2y^2 \right )}{dx}=\frac{d(a^2-(x-a)^2)}{dx}$
$4yy^{'}=4y\frac{dy}{dx}=-2(x-a)\\ \\$
$(x-a)= -2yy'\Rightarrow a = x+2yy'$ -(ii)
Put value from equation (ii) in (i)
$(-2yy')^2+2y^2= (x+2yy')^2\\ 4y^2(y')^2+2y^2= x^2+4y^2(y')^2+4xyy'\\ y' = \frac{2y^2-x^2}{4xy}$
Therefore, the required differential equation is $y' = \frac{2y^2-x^2}{4xy}$

Question:4 Prove that $x^2 - y^2 = c (x^2 + y^2 )^2$ is the general solution of differential equation $(x^3 - 3x y^2 ) dx = (y^3 - 3x^2 y) dy$ , where c is a parameter.

Answer:

Given,

$(x^3 - 3x y^2 ) dx = (y^3 - 3x^2 y) dy$

$\implies \frac{ dy}{dx} = \frac{(x^3 - 3x y^2 )}{(y^3 - 3x^2 y)}$

Now, let y = vx

$\implies \frac{ dy}{dx} = \frac{ d(vx)}{dx} = v + x\frac{dv}{dx}$

Substituting the values of y and y' in the equation,

$v + x\frac{dv}{dx} = \frac{(x^3 - 3x (vx)^2 )}{((vx)^3 - 3x^2 (vx))}$

$\\\implies v + x\frac{dv}{dx} = \frac{1 - 3v^2 }{v^3 - 3v}\\ \implies x\frac{dv}{dx} = \frac{1 - 3v^2 }{v^3 - 3v} -v = \frac{1 - v^4 }{v^3 - 3v}$

$\implies (\frac{v^3 - 3v }{1 - v^4})dv = \frac{dx}{x}$

Integrating both sides we get,

Now,

Let

$\implies$

Now,

Let v ² = p

1517901128803851

Now, substituting the values of I ₁ and I ₂ in the above equation, we get,

1517901129585614

Thus,

1517901130366853

1517901131127676

1517901132764415

$\\ (x^2 - y^2)^2 = C'^4(x^2 + y^2 )^4 \\ \implies (x^2 - y^2) = C'^2(x^2 + y^2 )^2 \\ \implies (x^2 - y^2) = K(x^2 + y^2 )^2, where\ K = C'^2$

Question:5 Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.

Answer:

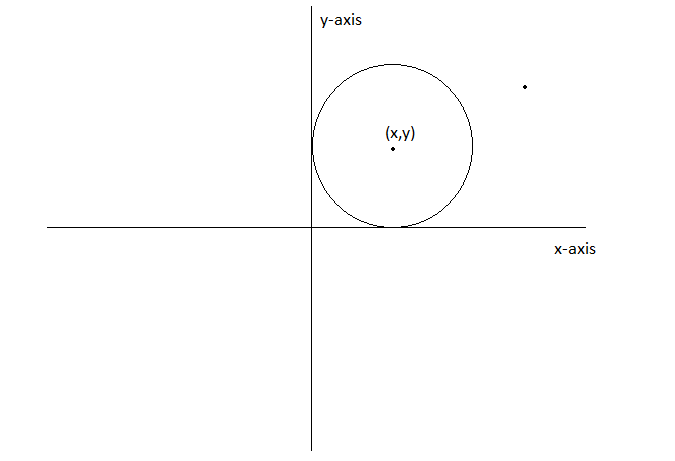1646973511355 Now, equation of the circle with center at (x,y) and radius r is
$(x-a)^2+(y-b)^2 = r^2$
Since, it touch the coordinate axes in first quadrant
Therefore, x = y = r
$(x-a)^2+(y-a)^2 = a^2$ -(i)
Differentiate it w.r.t x
we will get
$2(x-a)+2(y-a)y'= 0\\ \\ 2x-2a+2yy'-2ay' = 0\\ a=\frac{x+yy'}{1+y'}$ -(ii)
Put value from equation (ii) in equation (i)
$(x-\frac{x+yy'}{1+y'})^2+(y-\frac{x+yy'}{1+y'})^2=\left ( \frac{x+yy'}{1+y'} \right )^2\\ \\ (x+xy'-x-yy')^2+(y+yy'-x-yy')^2=(x+yy')^2\\ \\ (y')^2(x-y)^2+(x-y)^2=(x+yy')^2\\ \\ (x-y)^2\left ( (y')^2+1 \right )=(x+yy')^2$
Therefore, the differential equation of the family of circles in the first quadrant which touches the coordinate axes is $(x-y)^2\left ( (y')^2+1 \right )=(x+yy')^2$

Question:6 Find the general solution of the differential equation $\frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0$

Answer:

Given equation is
$\frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0$
we can rewrite it as
$\frac{dy}{dx } =- \sqrt{\frac{1-y^2}{1-x^2}}\\ \\ \frac{dy}{\sqrt{1-y^2}}= \frac{-dx}{\sqrt{1-x^2}}$
Now, integrate on both the sides
$\sin^{-1}y + C =- \sin ^{-1}x + C'\\ \\ \sin^{-1}y+\sin^{-1}x= C$
Therefore, the general solution of the differential equation $\frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0$ is $\sin^{-1}y+\sin^{-1}x= C$

Question:7 Show that the general solution of the differential equation $\frac{dy}{dx} + \frac{y^2 + y + 1}{x^2 + x + 1} = 0$ is given by $(x + y + 1) = A (1 - x - y - 2xy)$ , where A is parameter.

Answer:

Given,

$\frac{dy}{dx} + \frac{y^2 + y + 1}{x^2 + x + 1} = 0$

1517901142938688

Integrating both sides,

1517901146296446

1517901147071246

1517901148634163

1517901149451944

1517901150235484

1517901151028875

1517901151812195

Let

Let A = ,

Hence proved.

Question:8 Find the equation of the curve passing through the point $\left(0,\frac{\pi}{4} \right )$ whose differential equation is $\sin x \cos y dx + \cos x \sin y dy = 0.$

Answer:

Given equation is
$\sin x \cos y dx + \cos x \sin y dy = 0.$
we can rewrite it as
$\frac{dy}{dx}= -\tan x\cot y\\ \\ \frac{dy}{\cot y}= -\tan xdx\\ \\ \tan y dy =- \tan x dx$
Integrate both the sides
$\log |\sec y|+C' = -\log|sec x|- C''\\ \\ \log|\sec y | +\log|\sec x| = C\\ \\ \sec y .\sec x = e^{C}$
Now by using boundary conditiond, we will find the value of C
It is given that the curve passing through the point $\left(0,\frac{\pi}{4} \right )$
So,
$\sec \frac{\pi}{4} .\sec 0 = e^{C}\\ \\ \sqrt2.1= e^C\\ \\ C = \log \sqrt2$
Now,
$\sec y.\sec x= e^{\log \sqrt 2}\\ \\ \frac{\sec x}{\cos y} = \sqrt 2\\ \\ \cos y = \frac{\sec x}{\sqrt 2}$
Therefore, the equation of the curve passing through the point $\left(0,\frac{\pi}{4} \right )$ whose differential equation is $\sin x \cos y dx + \cos x \sin y dy = 0.$ is $\cos y = \frac{\sec x}{\sqrt 2}$

Question:9 Find the particular solution of the differential equation $(1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0$ , given that $y = 1$ when $x = 0$ .

Answer:

Given equation is
$(1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0$
we can rewrite it as
$\frac{dy}{dx}= -\frac{(1+y^2)e^x}{(1+e^{2x})}\\ \\ \frac{dy}{1+y^2}= \frac{-e^xdx}{1+e^{2x}}$
Now, integrate both the sides
$\tan^{-1}y + C' =\int \frac{-e^{x}dx}{1+e^{2x}}$
$\int \frac{-e^{x}dx}{1+e^{2x}}\\$
Put
$e^x = t \\ e^xdx = dt$
$\int \frac{dt}{1+t^2}= \tan^{-1}t + C''$
Put $t = e^x$ again
$\int \frac{-e^{x}dx}{1+e^{2x}} = -\tan ^{-1}e^x+C''$
Put this in our equation
$\tan^{-1}y = -\tan ^{-1}e^x+C\\ \tan^{-1}y +\tan ^{-1}e^x=C$
Now, by using boundary conditions we will find the value of C
It is given that
y = 1 when x = 0
$\\ \tan^{-1}1 +\tan ^{-1}e^0=C\\ \\ \frac{\pi}{4}+\frac{\pi}{4}= C\\ C = \frac{\pi}{2}$
Now, put the value of C

$\tan^{-1}y +\tan ^{-1}e^x=\frac{\pi}{2}$
Therefore, the particular solution of the differential equation $(1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0$ is $\tan^{-1}y +\tan ^{-1}e^x=\frac{\pi}{2}$

Question:10 Solve the differential equation $ye^\frac{x}{y}dx = \left(xe^\frac{x}{y} + y^2 \right )dy\ (y \neq 0)$

Answer:

Given,

$ye^\frac{x}{y}dx = (xe^\frac{x}{y} + y^2)dy$

$\\ ye^\frac{x}{y}\frac{dx}{dy} = xe^\frac{x}{y} + y^2 \\ \implies e^\frac{x}{y}[y\frac{dx}{dy} -x] = y^2 \\ \implies \frac{e^\frac{x}{y}[y\frac{dx}{dy} -x]}{y^2} = 1$

Let $\large e^\frac{x}{y} = t$

Differentiating it w.r.t. y, we get,

$\\ \frac{d}{dy}e^\frac{x}{y} = \frac{dt}{dy} \\ \implies e^\frac{x}{y}.\frac{d}{dy}(\frac{x}{y}) = \frac{dt}{dy} \\ \implies \frac{e^\frac{x}{y}[y\frac{dx}{dy} -x]}{y^2} =\frac{dt}{dy}$

Thus from these two equations,we get,

$\\ \frac{dt}{dy} = 1 \\ \implies \int dt = \int dy \\ \implies t = y + C$

Question:11 Find a particular solution of the differential equation $(x - y) (dx + dy) = dx - dy,$ , given that $y = -1$ , when $x = 0$ . (Hint: put $x - y = t$ )

Answer:

Given equation is
$(x - y) (dx + dy) = dx - dy,$
Now, integrate both the sides
Put
$(x-y ) = t\\ dx - dy = dt$
Now, given equation become
$dx+dy= \frac{dt}{t}$
Now, integrate both the sides
$x+ y + C '= \log t + C''$
Put $t = x- y$ again
$x+y = \log (x-y)+ C$
Now, by using boundary conditions we will find the value of C
It is given that
y = -1 when x = 0
$0+(-1) = \log (0-(-1))+ C\\ C = -1$
Now, put the value of C

$x+y = \log |x-y|-1\\ \log|x-y|= x+y+1$
Therefore, the particular solution of the differential equation $(x - y) (dx + dy) = dx - dy,$ is $\log|x-y|= x+y+1$

Question:12 Solve the differential equation $\left[\frac{e^{-2\sqrt x}}{\sqrt x} - \frac{y}{\sqrt x} \right ]\frac{dx}{dy} = 1\; \ (x\neq 0)$ .

Answer:

Given,

$\left[\frac{e^{-2\sqrt x}}{\sqrt x} - \frac{y}{\sqrt x} \right ]\frac{dx}{dy} = 1$

1517901190189935

1517901190951594

This is equation is in the form of

p = and Q =

Now, I.F. =

We know that the solution of the given differential equation is:

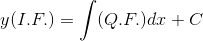
$y(I.F.) = \int(Q\timesI.F.)dx + C$

151790119561795

Question:13 Find a particular solution of the differential equation $\frac{dy}{dx} + y \cot x = 4x \textup{cosec} x\ (x\neq 0)$ , given that $y = 0 \ \textup{when}\ x = \frac{\pi}{2}$ .

Answer:

Given equation is
$\frac{dy}{dx} + y \cot x = 4x \textup{cosec} x\ (x\neq 0)$
This is $\frac{dy}{dx} + py = Q$ type where $p =\cot x$ and $Q = 4xcosec x$ $Q = 4x \ cosec x$
Now,
$I.F. = e^{\int pdx}= e^{\int \cot xdx}= e^{\log |\sin x|}= \sin x$
Now, the solution of given differential equation is given by relation
$y(I.F.) =\int (Q\times I.F.)dx +C$
$y(\sin x ) =\int (\sin x\times 4x \ cosec x)dx +C$
$y(\sin x) =\int(\sin x\times \frac{4x}{\sin x}) +C\\ \\ y(\sin x) = \int 4x + C\\ y\sin x= 2x^2+C$
Now, by using boundary conditions we will find the value of C
It is given that y = 0 when $x= \frac{\pi}{2}$
at $x= \frac{\pi}{2}$
$0.\sin \frac{\pi}{2 } = 2.\left ( \frac{\pi}{2} \right )^2+C\\ \\ C = - \frac{\pi^2}{2}$
Now, put the value of C
$y\sin x= 2x^2-\frac{\pi^2}{2}$
Therefore, the particular solution is $y\sin x= 2x^2-\frac{\pi^2}{2}, (sinx\neq0)$

Question:14 Find a particular solution of the differential equation $(x+1)\frac{dy}{dx} = 2e^{-y} -1$ , given that $y = 0$ when $x = 0$

Answer:

Given equation is
$(x+1)\frac{dy}{dx} = 2e^{-y} -1$
we can rewrite it as
$\frac{e^ydy}{2-e^y}= \frac{dx}{x+1}\\$
Integrate both the sides
$\int \frac{e^ydy}{2-e^y}= \log |x+1|\\$
$\int \frac{e^ydy}{2-e^y}$
Put
$2-e^y = t\\ -e^y dy = dt$
$\int \frac{-dt}{t}=- \log |t|$
put $t = 2- e^y$ again
$\int \frac{e^ydy}{2-e^y} =- \log |2-e^y|$
Put this in our equation
$\log |2-e^y| + C'= \log|1+x| + C''\\ \log (2-e^y)^{-1}= \log (1+x)+\log C\\ \frac{1}{2-e^y}= C(1+x)$

Now, by using boundary conditions we will find the value of C
It is given that y = 0 when x = 0
at x = 0
$\frac{1}{2-e^0}= C(1+0)\\ C = \frac{1}{2}$
Now, put the value of C
$\frac{1}{2-e^y} = \frac{1}{2}(1+x)\\ \\ \frac{2}{1+x}= 2-e^y\\ \frac{2}{1+x}-2= -e^y\\ -\frac{2x-1}{1+x} = -e^y\\ y = \log \frac{2x-1}{1+x}$
Therefore, the particular solution is $y = \log \frac{2x-1}{1+x}, x\neq-1$

Question:15 The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20, 000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?

Answer:

Let n be the population of the village at any time t.

According to question,

$\frac{dn}{dt} = kn\ \ (k\ is\ a\ constant)$

$\\ \implies \int \frac{dn}{n} = \int kdt \\ \implies \log n = kt + C$

Now, at t=0, n = 20000 (Year 1999)

$\\ \implies \log (20000) = k(0) + C \\ \implies C = \log2 + 4$

Again, at t=5, n= 25000 (Year 2004)

$\\ \implies \log (25000) = k(5) + \log2 + 4 \\ \implies \log 25 + 3 = 5k + \log2 +4 \\ \implies 5k = \log 25 - \log2 -1 =\log \frac{25}{20} \\ \implies k = \frac{1}{5}\log \frac{5}{4}$

Using these values, at t =10 (Year 2009)

$\\ \implies \log n = k(10)+ C \\ \implies \log n = \frac{1}{5}\log \frac{5}{4}(10) + \log2 + 4 \\ \implies \log n = \log(\frac{25.2.10000}{16}) = \log(31250) \\ \therefore n = 31250$

Therefore, the population of the village in 2009 will be 31250.

Question:16 The general solution of the differential equation $\frac{ydx - xdy}{y} = 0$ is

(A) $xy = C$

(B) $x = Cy^2$

(D) $y = Cx^2$

Answer:

Given equation is
$\frac{ydx - xdy}{y} = 0$
we can rewrite it as
$dx = \frac{x}{y}dy\\ \frac{dy}{y}=\frac{dx}{x}$
Integrate both the sides
we will get
$\log |y| = \log |x| + C\\ \log \frac{y}{x} = C \\ \frac{y}{x} = e^C\\ \frac{y}{x} = C\\ y = Cx$
Therefore, answer is (C)

Question:17 The general solution of a differential equation of the type $\frac{dx}{dy} + P_1 x = Q_1$ is

(A) $ye^{\int P_1 dy} = \int \left(Q_1 e^{\int P_1 dy} \right )dy +C$

(B) $ye^{\int P_1 dx} = \int \left(Q_1 e^{\int P_1 dx} \right )dx +C$

(D) $xe^{\int P_1 dx} = \int \left(Q_1 e^{\int P_1 dx} \right )dx +C$

Answer:

Given equation is
$\frac{dx}{dy} + P_1 x = Q_1$
and we know that the general equation of such type of differential equation is

$xe^{\int p_1dy} = \int (Q_1e^{\int p_1dy})dy+ C$
Therefore, the correct answer is (C)

Question:18 The general solution of the differential equation $e^x dy + (y e^x + 2x) dx = 0$ is

(A) $xe^y + x^2 = C$

(B) $xe^y + y^2 = C$

(D) $ye^y + x^2 = C$

Answer:

Given equation is
$e^x dy + (y e^x + 2x) dx = 0$
we can rewrite it as
$\frac{dy}{dx}+y=-2xe^{-x}$
It is $\frac{dy}{dx}+py=Q$ type of equation where $p = 1 \ and \ Q = -2xe^{-x}$
Now,
$I.F. = e^{\int p dx }= e^{\int 1dx}= e^x$
Now, the general solution is
$y(I.F.) = \int (Q\times I.F.)dx+C$
$y(e^x) = \int (-2xe^{-x}\times e^x)dx+C\\ ye^x= \int -2xdx + C\\ ye^x=- x^2 + C\\ ye^x+x^2 = C$
Therefore, (C) is the correct answer

If you want to get command on concepts then differential equations solutions of NCERT exercise are listed below

Differential Equations Class 12 - Topics

9.1 Introduction

9.2 Basic Concepts

9.2.1. Order of a differential equation

9.2.2 Degree of a differential equation

9.3. General and Particular Solutions of a Differential Equation

9.4 Formation of a Differential Equation whose General Solution is given

9.4.1 Procedure to form a differential equation that will represent a given family of curves

9.5. Methods of Solving First Order, First Degree Differential Equations

9.5.1 Differential equations with variables separable

9.5.2 Homogeneous differential equations

9.5.3 Linear differential equations

NCERT Exemplar Class 12 Solutions - Subject Wise

So, what is basically a differential equation? A differential equation is an equation in which derivatives of the dependent variable with respect to independent variables involved. Let's understand it with an example from NCERT chapter 9 differential equations-

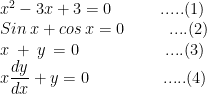
$\\x^2-3x+3=0\;\:\:\:\:\:\:\:\:\:\:\:\:.....(1)\\ Sin\:x+cos\:x=0\:\:\:\:\:\:\:\:\:\:\:\:....(2)\\x\:+\:y\:=0\;\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....(3)\\x\frac{dy}{dx}+y=0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....(4)$

From the above equations, we notice that equations (1), (2) and (3) involve dependent variable(variables) and/or independent only but equation (4) involves variables as well as derivative of the dependent variable (y) with respect to the independent variable (x). That type of equation is known as the differential equation.

Important terms used in class 12 chapter 9 differential equations-

Order of a differential equation - It is the order of the highest order derivative present in the equation.
Degree of a differential equation - It is the power of the highest order derivative in the differential equation.
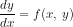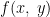Homogeneous differential equation - A differential equation that can be expressed in the form $\frac{dy}{dx}=f(x,\:y)$ where $f(x,\:y)$ is a homogeneous function of degree zero.
First order linear differential equation - A differential equation of the form 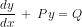$\dpi{80} \frac{dy}{dx}\:+\:Py=Q$ where P and Q are constants or functions of x only.

NCERT solutions for class 12 maths - Chapter Wise

chapter 1	NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
chapter 2	NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
chapter 3	NCERT solutions for class 12 maths chapter 3 Matrices
chapter 4	NCERT solutions for class 12 maths chapter 4 Determinants
chapter 5	NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
chapter 6	NCERT solutions for class 12 maths chapter 6 Application of Derivatives
chapter 7	NCERT solutions for class 12 maths chapter 7 Integrals
chapter 8	NCERT solutions for class 12 maths chapter 8 Application of Integrals
chapter 9	NCERT solutions for class 12 maths chapter 9 Differential Equations
chapter 10	NCERT solutions for class 12 maths chapter 10 Vector Algebra
chapter 11	NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
chapter 12	NCERT solutions for class 12 maths chapter 12 Linear Programming
chapter 13	NCERT solutions for class 12 maths chapter 13 Probability

Key Features of Class 12 Differential Equations NCERT Solutions – Differential Equations

Differential equations class 12 ncert solutions are designed to help students understand the various concepts and techniques involved in solving differential equations. Some of the key features of these solutions are:

Comprehensive coverage: The class 12 maths ch 9 question answer cover all the topics included in the Class 12 Maths syllabus, ensuring that students are well-prepared for their exams.
Simple language: The class 12 maths ch 9 question answer are written in simple language, making it easy for students to understand the concepts and techniques involved in solving differential equations.
Step-by-step approach: The class 12 differential equations solutions follow a step-by-step approach, which helps students to understand the solution process in a structured way.
Well-illustrated solutions: The maths chapter 9 class 12 solutions are accompanied by diagrams and illustrations, which help students to visualize the solution process and understand the concepts better.
Conceptual clarity: The maths chapter 9 class 12 solutions aim to develop the conceptual clarity of students, rather than just providing them with the final answers. This helps students to build a strong foundation in the subject.

NCERT solutions for class 12 subject wise

NCERT Solutions class wise

Tips to use NCERT Class 12 Maths Chapter 9 Solutions

NCERT solutions for class 12 maths chapter 9 differential equations are very helpful for the preparation of this chapter. Here are some tips to get command on it.

Differential equations are the easiest part of the class 12 calculus. If your concepts of integration are clear then it won't take much effort to get command on this chapter.
First, solve all NCERT problems including examples and miscellaneous exercise on your own. If you are not able to solve you can take the help of NCERT solutions for ch 9 maths class 12 differential equations which are provided here
If you have solved NCERT problems, you can solve previous years paper. It gives you an idea about the type of questions and difficulty levels of questions that have been asked in previous years

NCERT Books and NCERT Syllabus

Happy learning !!!

Frequently Asked Question (FAQs)

1. How the NCERT solutions are helpful in the board exam ?

As CBSE board exam paper is designed entirely based on NCERT textbooks and most of the questions in CBSE board exam are directly asked from NCERT textbook, students must know the NCERT very well to perform well in the exam. Only knowing the answer it not enough to perform well in the exam. In the NCERT solutions students will get know how best to write answer in the board exam in order to get good marks.

2. What is the weightage of the chapter Differential Equations for CBSE board exam ?

Generally, one question of 5 marks is asked from this chapter in the 12^thboard final exam. you should refer NCER syllabus for it. NCERT textbook and NCERT Notes are recommended if you want to obtain meritious marks in the Board exam.

3. What are the important topics in chapter Differential Equations ?

Basic concepts of differential equation, order and degree of the differential equation, general and particular solutions of a differential equation, formation of a differential equation, methods of solving first order,first degree differential equations, homogeneous differential equations and linear differential equations are the important topics of this chapter.

4. Are the answers to all the textbook questions available in the differential equations ncert solutions maths class 12 chapter 9?

The NCERT class 12 maths differential equations are available in PDF format and have been created by subject experts in line with the textbook questions. These solutions for ch 9 maths class 12 adhere to the latest CBSE Syllabus for 2023 and encompass all the significant concepts for the board exam. The problems in the textbook are solved step by step in accordance with the marks weightage in the CBSE Board exams. Careers360 website offers both chapter-wise and exercise-wise PDF links that can be used by students to instantly clarify their doubts.

Also Read

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism - Download PDF

NCERT Books for Class 12 Hindi 2024 - Download chapter wise PDFs here

NCERT Books for Class 12 Biology 2024 - Download Free PDF

NCERT Books for Class 12 Chemistry 2024 - Download Free Pdf

NCERT Book for Class 12 Maths 2024 - Download Free PDF

NCERT Book for Class 12 Physics 2024 - Download Free PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Syllabus for Class 12 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 12 2024 (All Subjects) - Download PDF Here

NCERT Syllabus for Class 6 to 12 (2023-24) - All Subjects PDF Download

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions for Class 12 Maths (Updated 2023-24)

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

CBSE Class 12 Result Verification & Revaluation 2024

May 04, 2024

GSEB HSC Marksheet 2024, Gujarat Board Class 12 Marksheet @gseb.org

May 04, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Certifications By Top Providers

Artificial Intelligence Projects

Via Great Learning

Introduction to Web Development with HTML CSS JavaScript

Via IBM

Introduction to Watson AI

Via IBM

Full-Stack Web Development

Via Masai School

Introduction to Data Science

Via IBM

Digital Banking Business Model

Via State Bank of India

1111 courses

788 courses

327 courses

141 courses

Harvard University, Cambridge

98 courses

IBM

85 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

History

Environmental Studies

Psychology

Data Science

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Lancaster University, Lancaster

Bailrigg, Lancaster LA1 4YW

Top Universities in Australia for International Students 2024 - QS Ranking

11 min ⋆ May 02, 2024 12:05 PM IST

SAT Exam Fees 2024 - Registration, Late, Cancellation, Score Services Fee

4 min ⋆ Mar 11, 2024 07:03 AM IST

SAT Sample Papers 2024 - Question Papers PDF for SAT Practice Test

7 min ⋆ May 02, 2024 11:05 AM IST

Top Universities in Canada for International Students 2024 - QS Ranking

9 min ⋆ May 02, 2024 10:05 AM IST

Study MBBS in USA for Indian and International Students 2024

14 min ⋆ Feb 01, 2024 04:02 AM IST

How to Apply for Eligibility Certificate for Studying MBBS Abroad?

6 min ⋆ May 02, 2024 09:05 AM IST

Related E-books & Sample Papers

CBSE Class 11, 12 Physics Syllabus 2024-25

240+ Downloads

CBSE Class 11, 12 Economics Syllabus 2024-25

87+ Downloads

CBSE Class 11, 12 Sociology Syllabus 2024-25

108+ Downloads

CBSE Class 11, 12 Sanskrit (Elective) Syllabus 2024-25

31+ Downloads

CBSE Class 11, 12 Sanskrit (Core) Syllabus 2024-25

9+ Downloads

CBSE Class 11, 12 Psychology Syllabus 2024-25

35+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer

Sajal Trivedi 29 January,2024

i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer

Upasana Barman 24 August,2022

i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.

As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.

Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.

Believe in Yourself! You can make anything happen

All the very best.

Read Complete Answer

Mayankjha.student2007 23 August,2022

if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer

Nuthalapati Vyshnavi 21 August,2022

I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer

Muskan Dhalwal 17 August,2022

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

300M+
Students
36,000+
Colleges
550+
Exams
1500+
E-Books
16000+
Certifications

We Appeared in

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations

NCERT Differential Equations Class 12 Questions And Answers

Applications for Admissions are open.

ALLEN NEET Coaching

Aakash iACST Scholarship Test 2024

NCERT Differential Equations Class 12 Questions And Answers PDF Free Download

NCERT Differential Equations Class 12 Questions And Answers - Important Formulae

SAT® | CollegeBoard

TOEFL ® Registrations 2024

NCERT Differential Equations Class 12 Questions And Answers (Intext Questions and Exercise)

More About NCERT Solutions for Class 12 Maths Chapter 9

Differential Equations Class 12 - Topics

NCERT Exemplar Class 12 Solutions - Subject Wise

NCERT solutions for class 12 maths - Chapter Wise

Key Features of Class 12 Differential Equations NCERT Solutions – Differential Equations

NCERT solutions for class 12 subject wise

NCERT Solutions class wise

Tips to use NCERT Class 12 Maths Chapter 9 Solutions