Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • School
  • Provide Solution for RD Sharma Class 12 Chapter 29 Linear Programming Exercise 29.4 Question 37

Provide Solution for RD Sharma Class 12 Chapter 29 Linear Programming Exercise 29.4 Question 37

Answers (1)

Answer:

 The minimum transportation cost is 4400.

Hint:

Assuming that the transportation cost of 50 liters of oil is Rs.1 per km.

Given:

 

Distance

(in km)

To/From

A

B

D

7

3

E

6

4

F

3

2

Solution:                   

Let x and y liters of oil be supplied from A to the petrol pumps, D and E. Then, (7000-x-y) will be supplied from A to petrol pump F. The requirement at petrol pump D is 4500l since xl are transported from depot A, the remaining (7000-x) will be transported from petrol pump B.

Similarly, (3000-y)l and 35000-(7000-x-y)=(x+y-3500)l will be transported from depot B to petrol pump E and F respectively. The given problem can be represented diagrammatically as follows.

                     

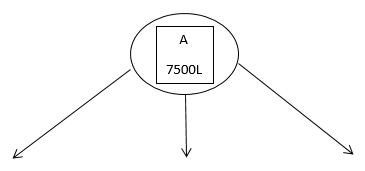
\begin{aligned} & x \geq 0, y \geq 0, \text { and }(7000-x-y) \geq 0 \\ \Rightarrow \quad & x \geq 0, y \geq 0 \text { and } x+y \leq 7000 \\ & 4500-x \geq 0,3000-y \geq 0, \text { and } x+y-3500 \geq 0 \\ \Rightarrow & x \leq 4500, y \leq 3000 \text { and } x+y \geq 3500 \end{aligned}

 

Cost of transporting 10 litres of petrol = Rs.1

 

Cost of transporting 1 litre of petrol = \frac{1}{10} \mathrm{Rs}

Therefore, total transportation cost is given by,

\! \! \! \! \! \! \! \! z=\! \frac{1}{10}, x+\frac{6}{10} y+\frac{3}{10}(7000-\! x-y)+\frac{3}{10}(4500-x)+\! \frac{4}{10}(3000-\! y)+\frac{2}{10}(x+y-3500) 

 = 0.3x + 0.1y + 3950

The problem can be formulated as follows.

Minimize Z=0.3x + 0.1y + 3950                                            …(i)

Subject to the constraints

x+y \leq 7000                                                                              … (ii)

\begin{aligned} &\\ &x \leq 4500 \end{aligned}                                                                                     … (iii)

\begin{aligned} &y \leq 3000 \\ & \end{aligned}                                                                                     … (iv)

x+y \geq 3500 \\                                                                              … (v)

x \geq 0, y \geq 0                                                                                 … (vi)

The feasible region determined by the constraints as follows

The corner points of the feasible region are A(3500,0), B(4500,0), C(4500,2500), D(4000,3000) and E(500,3000)

The values at the corner points as follows:

Corner Points

Z=0.3x+0.1y+3950

 

A(3500,0)

5000

 

B(4500,0)

5300

 

C(4500,2500)

5550

 

D(4000,3000)

0+20=20

 

E(500,3000)

4400

Minimum

 

The minimum value of Z is 4400 at (500, 3000)

Thus the oil supplied from depot A is 500L, 3000L and 3500L and from depot B is 400L, 0L and 0L petrol pumps D,E and F respectively.

The minimum transportation cost is Rs.4400.

 

Posted by

infoexpert27

View full answer

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

Similar Questions

Trending Articles/News

anam-khan

CBSE Class 12 result verification 2024 application out at cbse.gov.in; last date, fees
anam-khan

CBSE results 2024 later for 102 students over fake certificates; board issues show cause notice
anam-khan

What after CBSE Class 12 results 2024? From CUET UG to JEE Advanced, all you need to know

Latest Question