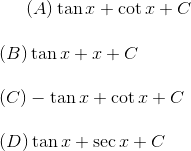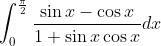Apply to Aakash iACST Scholarship Test 2024
NCERT Solutions for Class 12 Maths Chapter 7 Integrals
NCERT Integrals Class 12 Questions And Answers
NCERT Solutions for Class 12 Maths Chapter 7 Integrals are discussed here. This chapter deals with definite and indefinite integrals. Integration class 12 also includes elementary properties of integration including basic techniques of integration. NCERT Class 12 maths chapter 7 solutions will be very helpful when you are solving the questions from NCERT books for Class 12 Maths. These NCERT Class 12 Maths solutions chapter 7 are prepared by subject matter experts that are very easy to understand. students can practice integrals class 12 ncert solutions to get good hold on the concepts.
- NCERT Integrals Class 12 Questions And Answers
- NCERT Integrals Class 12 Questions And Answers PDF Free Download
- Class 12 maths chapter 7 NCERT Solutions - Important Formulae
- NCERT Integrals Class 12 Questions And Answers (Intext Questions and Exercise)
- NCERT Solutions for Class 12 Maths Chapter 7 Integrals - Topics
- NCERT solutions for class 12 maths - Chapter wise
- Key Features of NCERT Solutions for Class 12 Maths Chapter 7 Integrals
- NCERT solutions for class 12 - subject wise
- NCERT Books and NCERT Syllabus

NCERT solutions for class 12 math chapter 7 integrals are important for board exams as well as for competitive examinations like JEE Main, VITEEE, BITSAT, etc but without command, on the concepts of integrals ncert solutions meritorious marks cant be scoured. Therefore chapter 7 maths class 12 is recommended to students. Also, you can check the NCERT solutions for other Classes here.
Also read:
- Class 12 Maths Chapter 7 Integrals Notes
- Ncert Exemplar Solutions For Class 12 Maths Chapter 7 Integrals
NCERT Integrals Class 12 Questions And Answers PDF Free Download
Class 12 maths chapter 7 NCERT Solutions - Important Formulae
>> Integration as Inverse of Differentiation: Integration is the inverse process of differentiation.
In differential calculus, we find the derivative of a given function, while in integral calculus, we find a function whose derivative is given.
Indefinite Integrals:
∫f(x) dx = F(x) + C
These integrals are called indefinite integrals or general integrals.
C is an arbitrary constant that leads to different anti-derivatives of the given function.
Multiple Anti-Derivatives:
A derivative of a function is unique, but a function can have infinite anti-derivatives or integrals.
Properties of Indefinite Integral:
∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx
For any real number k, ∫k f(x) dx = k∫f(x)dx.
In general, if f1, f2, …, fn are functions and k1, k2, …, kn are real numbers, then ∫[k1f1(x) + k2f2(x) + … + knfn(x)] dx = k1 ∫f1(x) dx + k2 ∫f2(x) dx + … + kn ∫fn(x) dx
First Fundamental Theorem of Integral Calculus:
Define the area function A(x) = ∫[a, x]f(t)dt for x ≥ a, where f is continuous on [a, b].
Then A'(x) = f(x) for every x ∈ [a, b].
Second Fundamental Theorem of Integral Calculus:
If f is a continuous function on [a, b], then ∫[a, b]f(x)dx = F(b) - F(a), where F(x) is an antiderivative of f(x).
Standard Integral Formulas:
∫xn dx = xn+1/(n+1) + C (n ≠ -1)
∫cos x dx = sin x + C
∫sin x dx = -cos x + C
∫sec2 x dx = tan x + C
∫cosec2 x dx = -cot x + C
∫sec x tan x dx = sec x + C
∫cosec x cot x dx = -cosec x + C
∫ex dx = ex + C
∫ax dx = (ax)/ln(a) + C
∫(1/x) dx = ln|x| + C
Other Integral Formulas:
∫tan x dx = ln|sec x| + C
∫cot x dx = ln|sin x| + C
∫sec x dx = ln|sec x + tan x| + C
∫cosec x dx = ln|cosec x - cot x| + C
Free download Class 12 Maths Chapter 7 Question Answer for CBSE Exam.
NCERT Integrals Class 12 Questions And Answers (Intext Questions and Exercise)
Class 12 Integrals NCERT solutions Exercise: 7.1
Question:1 Find an anti derivative (or integral) of the following functions by the method of inspection.
Answer:
GIven ;
So, the anti derivative of is a function of x whose derivative is
.
Therefore, we have
Or, antiderivative of is
.
Question:2 Find an anti derivative (or integral) of the following functions by the method of inspection. 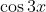
Answer:
GIven ;
So, the antiderivative of is a function of x whose derivative is
.
Therefore, we have the anti derivative of is
.
Question:3 Find an anti derivative (or integral) of the following functions by the method of inspection. 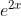
Answer:
GIven ;
So, the anti derivative of is a function of x whose derivative is
.
Therefore, we have the anti derivative of is
.
Question:4 Find an anti derivative (or integral) of the following functions by the method of inspection. 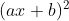
Answer:
GIven ;
So, the anti derivative of is a function of x whose derivative is
.
Therefore, we have the anti derivative of is
.
Question:5 Find an anti derivative (or integral) of the following functions by the method of inspection. 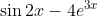
Answer:
GIven ;
So, the anti derivative of is a function of x whose derivative is
.
Therefore, we have the anti derivative of is
.
Question:6 Find the following integrals
Answer:
Given intergral ;
or , where C is any constant value.
Question:7 Find the following integrals 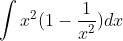
Answer:
Given intergral ;
or , where C is any constant value.
Question:8 Find the following integrals 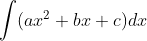
Answer:
Given intergral ;
or , where C is any constant value.
Question:9 Find the following integrals intergration of 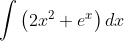
Answer:
Given intergral ;
or , where C is any constant value.
Question:10 Find the following integrals 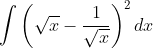
Answer:
Given integral ;
or
, where C is any constant value.
Question:11 Find the following integrals intergration of 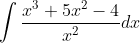
Answer:
Given intergral ;
or
Or, , where C is any constant value.
Question:12 Find the following integrals 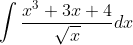
Answer:
Given intergral ;
or
Or, , where C is any constant value.
Question:13 Find the following integrals intergration of 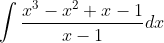
Answer:
Given integral
It can be written as
Taking common out
Now, cancelling out the term from both numerator and denominator.
Splitting the terms inside the brackets
Question:14 Find the following integrals 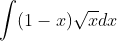
Answer:
Given intergral ;
or
, where C is any constant value.
Question:15 Find the following integrals 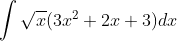
Answer:
Given intergral ;
or
, where C is any constant value.
Question:16 Find the following integrals 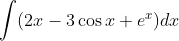
Answer:
Given integral ;
splitting the integral as the sum of three integrals
, where C is any constant value.
Question:18 Find the following integrals 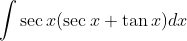
Answer:
Given integral ;
Using the integral of trigonometric functions
, where C is any constant value.
Question:19 Find the following integrals intergration of 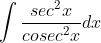
Answer:
Given integral ;
, where C is any constant value.
Question:20 Find the following integrals 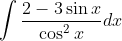
Answer:
Given integral ;
Using antiderivative of trigonometric functions
, where C is any constant value.
Question:21 Choose the correct answer
The anti derivative of 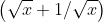 equals
equals
Answer:
Given to find the anti derivative or integral of ;
, where C is any constant value.
Hence the correct option is (C).
Question:22 Choose the correct answer The anti derivative of
If such that f (2) = 0. Then f (x) is
Answer:
Given that the anti derivative of
So,
Now, to find the constant C;
we will put the condition given, f (2) = 0
or
Therefore the correct answer is A .
Class 12 Integrals NCERT solutions Exercise: 7.2
Question:1 Integrate the functions 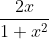
Answer:
Given to integrate function,
Let us assume
we get,
now back substituting the value of
as is positive we can write
Question:2 Integrate the functions 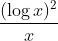
Answer:
Given to integrate function,
Let us assume
we get,
Question:4 Integrate the functions 
Answer:
Given to integrate function,
Let us assume
we get,
Back substituting the value of t we get,
Question:5 Integrate the functions 
Answer:
Given to integrate function,
Let us assume
we get,
Now, by back substituting the value of t,
Question:6 Integrate the functions 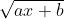
Answer:
Given to integrate function,
Let us assume
we get,
Now, by back substituting the value of t,
Question:7 Integrate the functions 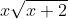
Answer:
Given function ,
Assume the 19634
Back substituting the value of t in the above equation.
or, , where C is any constant value.
Question:8 Integrate the functions 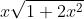
Answer:
Given function ,
Assume the
Or
, where C is any constant value.
Question:9 Integrate the functions 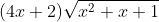
Answer:
Given function ,
Assume the
Now, back substituting the value of t in the above equation,
, where C is any constant value.
Question:10 Integrate the functions 
Answer:
Given function ,
Can be written in the form:
Assume the
, where C is any constant value.
Question:11 Integrate the functions 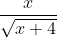 , x > 0
, x > 0
Answer:
Given function ,
Assume the so,
, where C is any constant value.
Question:12 Integrate the functions 
Answer:
Given function ,
Assume the
, where C is any constant value.
Question:13 Integrate the functions 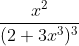
Answer:
Given function ,
Assume the
, where C is any constant value.
Question:14 Integrate the functions 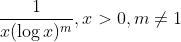
Answer:
Given function ,
Assume the
, where C is any constant value.
Question:15 Integrate the functions 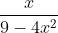
Answer:
Given function ,
Assume the
Now back substituting the value of t ;
, where C is any constant value.
Question:16 Integrate the functions 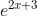
Answer:
Given function ,
Assume the
Now back substituting the value of t ;
, where C is any constant value.
Question:17 Integrate the functions 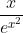
Answer:
Given function ,
Assume the
, where C is any constant value.
Question:19 Integrate the functions 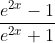
Answer:
Given function ,
Simplifying it by dividing both numerator and denominator by , we obtain
Assume the
Now, back substituting the value of t,
, where C is any constant value.
Question:20 Integrate the functions 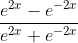
Answer:
Given function ,
Assume the
Now, back substituting the value of t,
, where C is any constant value.
Question:21 Integrate the functions 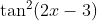
Answer:
Given function ,
Assume the
Now, back substituting the value of t,
or , where C is any constant value.
Question:22 Integrate the functions 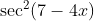
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:23 Integrate the functions 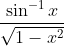
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:24 Integrate the functions 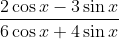
Answer:
Given function ,
or simplified as
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:25 Integrate the functions 
Answer:
Given function ,
or simplified as
Assume the
Now, back substituted the value of t.
where C is any constant value.
Question:26 Integrate the functions 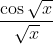
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:27 Integrate the functions 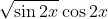
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:28 Integrate the functions 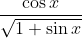
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:29 Integrate the functions 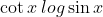
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:30 Integrate the functions 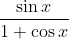
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:31 Integrate the functions 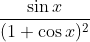
Answer:
Given function ,
Assume the
Now, back substituted the value of t.
, where C is any constant value.
Question:32 Integrate the functions 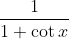
Answer:
Given function
Assume that
Now solving the assumed integral;
Now, to solve further we will assume
Or,
Now, back substituting the value of t,
Question:33 Integrate the functions 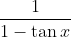
Answer:
Given function
Assume that
Now solving the assumed integral;
Now, to solve further we will assume
Or,
Now, back substituting the value of t,
Question:34 Integrate the functions 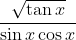
Answer:
Given function
Assume that
Now solving the assumed integral;
Multiplying numerator and denominator by ;
Now, to solve further we will assume
Or,
Now, back substituting the value of t,
Question:35 Integrate the functions 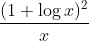
Answer:
Given function
Assume that
Now, back substituting the value of t,
Question:36 Integrate the functions 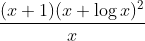
Answer:
Given function
Simplifying to solve easier;
Assume that
Now, back substituting the value of t,
Question:37 Integrate the functions 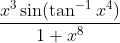
Answer:
Given function
Assume that
......................(1)
Now to solve further we take
So, from the equation (1), we will get
Now back substitute the value of u,
and then back substituting the value of t,
Question:38 Choose the correct answer 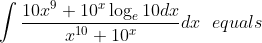
Answer:
Given integral
Taking the denominator
Now differentiating both sides we get
Back substituting the value of t,
Therefore the correct answer is D.
Class 12 Integrals NCERT Solutions Exercise: 7.3
Question:1 Find the integrals of the functions 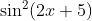
Answer:
using the trigonometric identity
we can write the given question as
=
Question:2 Find the integrals of the functions 
Answer:
Using identity
, therefore the given integral can be written as
Question:3 Find the integrals of the functions 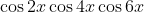
Answer:
Using identity
Again use the same identity mentioned in the first line
Question:4 Find the integrals of the functions 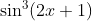
Answer:
The integral can be written as
Let
Now, replace the value of t, we get;
Question:5 Find the integrals of the functions 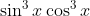
Answer:
rewrite the integral as follows
Let
......(replace the value of t as
)
Question:6 Find the integrals of the functions 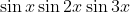
Answer:
Using the formula
we can write the integral as follows
Question:7 Find the integrals of the functions 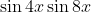
Answer:
Using identity
we can write the following integral as
=
Question:8 Find the integrals of the functions 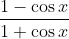
Answer:
We know the identities
Using the above relations we can write
Question:9 Find the integrals of the functions 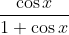
Answer:
The integral is rewritten using trigonometric identities
Question:10 Find the integrals of the functions 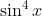
Answer:
can be written as follows using trigonometric identities
Therefore,
Question:11 Find the integrals of the functions 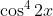
Answer:
now using the identity
now using the below two identities
the value
.
the integral of the given function can be written as
Question:12 Find the integrals of the functions 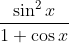
Answer:
Using trigonometric identities we can write the given integral as follows.
Question:13 Find the integrals of the functions 
Answer:
We know that,
Using this identity we can rewrite the given integral as
Question:15 Find the integrals of the functions 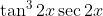
Answer:
Therefore integration of =
.....................(i)
Let assume
So, that
Now, the equation (i) becomes,
Question:16 Find the integrals of the functions 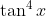
Answer:
the given question can be rearranged using trigonometric identities
Therefore, the integration of =
...................(i)
Considering only
let
now the final solution is,
Question:17 Find the integrals of the functions 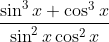
Answer:
now splitting the terms we can write
Therefore, the integration of
Question:18 Find the integrals of the functions 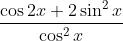
Answer:
The integral of the above equation is
Thus after evaluation, the value of integral is tanx+ c
Question:19 Find the integrals of the functions 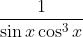
Answer:
Let
We can write 1 =
Then, the equation can be written as
put the value of tan = t
So, that
Question:20 Find the integrals of the functions 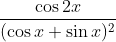
Answer:
we know that
therefore,
let
Now the given integral can be written as
Question:21 Find the integrals of the functions 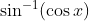
Answer:
using the trigonometric identities we can evaluate the following integral as follows
Question:22 Find the integrals of the functions 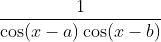
Answer:
Using the trigonometric identities following integrals can be simplified as follows
Question:23 Choose the correct answer
Answer:
The correct option is (A)
On reducing the above integral becomes
NCERT solutions for maths chapter 7 class 12 Integrals Exercise: 7.4
Question:1 Integrate the functions 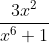
Answer:
The given integral can be calculated as follows
Let
, therefore,
Question:2 Integrate the functions 
Answer:
let suppose 2x = t
therefore 2dx = dt
.................using formula
Question:4 Integrate the functions 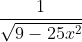
Answer:
Let assume 5x =t,
then 5dx = dt
The above result is obtained using the identity
Question:6 Integrate the functions 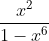
Answer:
let
then
using the special identities we can simplify the integral as follows
Question:7 Integrate the functions 
Answer:
We can write above eq as
............................................(i)
for let
Now, by using eq (i)
Question:8 Integrate the functions 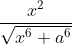
Answer:
The integration can be down as follows
let
........................using
Question:10 Integrate the functions 
Answer:
the above equation can be also written as,
let 1+x = t
then dx = dt
therefore,
Question:11 Integrate the functions 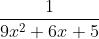
Answer:
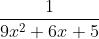
this denominator can be written as
![9x^2+6x+5=9[x^2+\frac{2}{3}x+\frac{5}{9}]\\=9[(x+\frac{1}{3})^2+(\frac{2}{3})^2]](https://entrancecorner.oncodecogs.com/gif.latex?9x%5E2+6x+5%3D9%5Bx%5E2+%5Cfrac%7B2%7D%7B3%7Dx+%5Cfrac%7B5%7D%7B9%7D%5D%5C%5C%3D9%5B%28x+%5Cfrac%7B1%7D%7B3%7D%29%5E2+%28%5Cfrac%7B2%7D%7B3%7D%29%5E2%5D) Now,
Now,
![\frac{1}{9}\int \frac{1}{(x+\frac{1}{3})^2+(\frac{2}{3})^2}dx =\frac{1}{9} [\frac{3}{2}\tan^{-1}(\frac{(x+1/3)}{2/3})] +C\\=\frac{1}{6} \tan^{-1}(\frac{3x+1}{2})] +C](https://entrancecorner.oncodecogs.com/gif.latex?%5Cfrac%7B1%7D%7B9%7D%5Cint%20%5Cfrac%7B1%7D%7B%28x+%5Cfrac%7B1%7D%7B3%7D%29%5E2+%28%5Cfrac%7B2%7D%7B3%7D%29%5E2%7Ddx%20%3D%5Cfrac%7B1%7D%7B9%7D%20%5B%5Cfrac%7B3%7D%7B2%7D%5Ctan%5E%7B-1%7D%28%5Cfrac%7B%28x+1/3%29%7D%7B2/3%7D%29%5D%20+C%5C%5C%3D%5Cfrac%7B1%7D%7B6%7D%20%5Ctan%5E%7B-1%7D%28%5Cfrac%7B3x+1%7D%7B2%7D%29%5D%20+C)
......................................by using the form 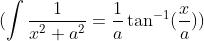
Question:12 Integrate the functions 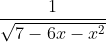
Answer:
the denominator can be also written as,
therefore
Let x+3 = t
then dx =dt
......................................using formula
Question:13 Integrate the functions 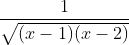
Answer:
(x-1)(x-2) can be also written as
=
=
therefore
let suppose
Now,
.............by using formula
Question:16 Integrate the functions 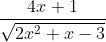
Answer:
let
By equating the coefficient of x and constant term on each side, we get
A = 1 and B=0
Let
Question:17 Integrate the functions 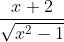
Answer:
let
By comparing the coefficients and constant term on both sides, we get;
A=1/2 and B=2
then
Question:18 Integrate the functions 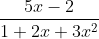
Answer:
let
By comparing the coefficients and constants we get the value of A and B
A = and B =
NOW,
...........................(i)
put
Thus
Question:19 Integrate the functions 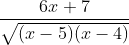
Answer:
let
By comparing the coefficients and constants on both sides, we get
A =3 and B =34
....................................(i)
Considering
let
Now consider
here the denominator can be also written as
Dr =
Now put the values of and
in eq (i)
Question:20 Integrate the functions 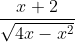
Answer:
let
By equating the coefficients and constant term on both sides we get
A = -1/2 and B = 4
(x+2) = -1/2(4-2x)+4
....................(i)
Considering
let
now,
put the value of and
Question:21 Integrate the functions 
Answer:
...........(i)
take
let
considering
putting the values in equation (i)
Question:22 Integrate the functions 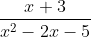
Answer:
Let
By comparing the coefficients and constant term, we get;
A = 1/2 and B =4
..............(i)
put
Question:23 Integrate the functions 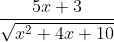
Answer:
let
On comparing, we get
A =5/2 and B = -7
...........................................(i)
put
Question:24 Choose the correct answer
Answer:
The correct option is (B)
the denominator can be written as
now,
Question:25 Choose the correct answer 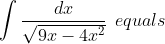
Answer:
The following integration can be done as
The correct option is (B)
NCERT solutions for maths chapter 7 class 12 Integrals Exercise: 7.5
Question:1 Integrate the rational functions
Answer:
Given function
Partial function of this function:
Now, equating the coefficients of x and constant term, we obtain
On solving, we get
Question:2 Integrate the rational functions 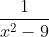
Answer:
Given function
The partial function of this function:
Now, equating the coefficients of x and constant term, we obtain
On solving, we get
Question:3 Integrate the rational functions 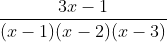
Answer:
Given function
Partial function of this function:
.(1)
Now, substituting respectively in equation (1), we get
That implies
Question:4 Integrate the rational functions 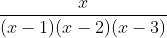
Answer:
Given function
Partial function of this function:
.....(1)
Now, substituting respectively in equation (1), we get
That implies
Question:5 Integrate the rational functions 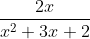
Answer:
Given function
Partial function of this function:
...........(1)
Now, substituting respectively in equation (1), we get
That implies
Question:6 Integrate the rational functions 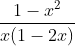
Answer:
Given function
Integral is not a proper fraction so,
Therefore, on dividing by
, we get
Partial function of this function:
...........(1)
Now, substituting respectively in equation (1), we get
No, substituting in equation (1) we get
Question:7 Integrate the rational functions 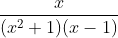
Answer:
Given function
Partial function of this function:
Now, equating the coefficients of and the constant term, we get
and
On solving these equations, we get
From equation (1), we get
Now, consider ,
and we will assume
So,
or
Question:8 Integrate the rational functions 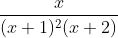
Answer:
Given function
Partial function of this function:
Now, putting in the above equation, we get
By equating the coefficients of and constant term, we get
then after solving, we get
Therefore,
Question:9 Integrate the rational functions 
Answer:
Given function
can be rewritten as
Partial function of this function:
................(1)
Now, putting in the above equation, we get
By equating the coefficients of and
, we get
then after solving, we get
Therefore,
Question:10 Integrate the rational functions 
Answer:
Given function
can be rewritten as
The partial function of this function:
Equating the coefficients of , we get
Therefore,
Question:11 Integrate the rational functions 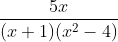
Answer:
Given function
can be rewritten as
The partial function of this function:
Now, substituting the value of respectively in the equation above, we get
Therefore,
Question:12 Integrate the rational functions 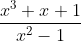
Answer:
Given function
As the given integral is not a proper fraction.
So, we divide by
, we get
can be rewritten as
....................(1)
Now, substituting in equation (1), we get
Therefore,
Question:13 Integrate the rational functions 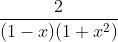
Answer:
Given function
can be rewritten as
....................(1)
Now, equating the coefficient of and constant term, we get
,
, and
Solving these equations, we get
Therefore,
Question:14 Integrate the rational functions 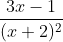
Answer:
Given function
can be rewritten as
Now, equating the coefficient of and constant term, we get
and
,
Solving these equations, we get
Therefore,
Question:15 Integrate the rational functions 
Answer:
Given function
can be rewritten as
The partial fraction of above equation,
Now, equating the coefficient of and constant term, we get
and
and
Solving these equations, we get
Therefore,
Question:16 Integrate the rational functions 
[Hint: multiply numerator and denominator by and put
]
Answer:
Given function
Applying Hint multiplying numerator and denominator by and putting
Putting
can be rewritten as
Partial fraction of above equation,
................(1)
Now, substituting in equation (1), we get
Question:17 Integrate the rational functions 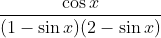
Answer:
Given function
Applying the given hint: putting
We get,
Partial fraction of above equation,
................(1)
Now, substituting in equation (1), we get
Back substituting the value of t in the above equation, we get
Question:18 Integrate the rational functions 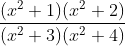
Answer:
Given function
We can rewrite it as:
Partial fraction of above equation,
Now, equating the coefficients of and constant term, we get
,
,
,
After solving these equations, we get
Question:19 Integrate the rational functions 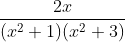
Answer:
Given function
Taking
The partial fraction of above equation,
..............(1)
Now, substituting in equation (1), we get
Question:20 Integrate the rational functions 
Answer:
Given function
So, we multiply numerator and denominator by , to obtain
Now, putting
we get,
Taking
Partial fraction of above equation,
..............(1)
Now, substituting in equation (1), we get
Back substituting the value of t,
Question:21 Integrate the rational functions 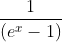 [Hint : Put
[Hint : Put 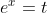 ]
]
Answer:
Given function
So, applying the hint: Putting
Then
Partial fraction of above equation,
..............(1)
Now, substituting in equation (1), we get
Now, back substituting the value of t,
Question:22 Choose the correct answer 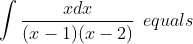
Answer:
Given integral
Partial fraction of above equation,
..............(1)
Now, substituting in equation (1), we get
Therefore, the correct answer is B.
Question:23 Choose the correct answer 
Answer:
Given integral
Partial fraction of above equation,
Now, equating the coefficients of and the constant term, we get
,
,
We have the values,
Therefore, the correct answer is A.
NCERT solutions for maths chapter 7 class 12 Integrals Exercise: 7.6
Question:1 Integrate the functions
Answer:
Given function is
We will use integrate by parts method
Therefore, the answer is
Question:2 Integrate the functions 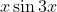
Answer:
Given function is
We will use integration by parts method
Therefore, the answer is
Question:3 Integrate the functions 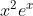
Answer:
Given function is
We will use integration by parts method
Again use integration by parts in
Put this value in our equation
we will get,
Therefore, answer is
Question:4 Integrate the functions 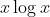
Answer:
Given function is
We will use integration by parts method
Therefore, the answer is
Question:5 Integrate the functions 
Answer:
Given function is
We will use integration by parts method
Therefore, the answer is
Question:6 Integrate the functions 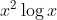
Answer:
Given function is
We will use integration by parts method
Therefore, the answer is
Question:7 Integrate the functions 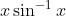
Answer:
Given function is
We will use integration by parts method
Now, we need to integrate
Put this value in our equation
Therefore, the answer is
Question:8 Integrate the functions 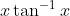
Answer:
Given function is
We will use integration by parts method
Put this value in our equation
Therefore, the answer is
Question:9 Integrate the functions 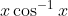
Answer:
Given function is
We will use integration by parts method
Now, we need to integrate
Put this value in our equation
Therefore, the answer is
Question:10 Integrate the functions 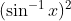
Answer:
Given function is
we will use integration by parts method
Therefore, answer is
Question:11 Integrate the functions 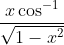
Answer:
Consider
So, we have then:
After taking as a first function and
as second function and integrating by parts, we get
Or, 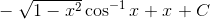
Question:12 Integrate the functions 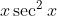
Answer:
Consider
So, we have then:
After taking as a first function and
as second function and integrating by parts, we get
Question:13 Integrate the functions 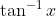
Answer:
Consider
So, we have then:
After taking as a first function and
as second function and integrating by parts, we get
Question:14 Integrate the functions 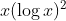
Answer:
Consider
So, we have then:
After taking as a first function and
as second function and integrating by parts, we get
Question:15 Integrate the functions 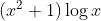
Answer:
Consider
So, we have then:
Let us take ....................(1)
Where, and
So,
After taking as a first function and
as second function and integrating by parts, we get
....................(2)
After taking as a first function and
as second function and integrating by parts, we get
................(3)
Now, using the two equations (2) and (3) in (1) we get,
Question:16 Integrate the functions 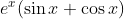
Answer:
Let suppose
we know that,
Thus, the solution of the given integral is given by
Question:17 Integrate the functions 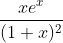
Answer:
Let suppose
by rearranging the equation, we get
let
It is known that
therefore the solution of the given integral is
Question:18 Integrate the functions 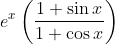
Answer:
Let
substitute and
let
It is known that
Therefore the solution of the given integral is
Question:19 Integrate the functions 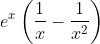
Answer:
It is known that
let
Therefore the required solution of the given above integral is
Question:20 Integrate the functions 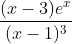
Answer:
It is known that
So, By adjusting the given equation, we get
to let
Therefore the required solution of the given integral is
Question:22 Integrate the functions 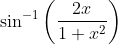
Answer:
let
Taking as a first function and
as a second function, by using by parts method
Question:24 Choose the correct answer
Answer:
we know that,
from above integral
let
thus, the solution of the above integral is
NCERT class 12 maths ch 7 question answer Exercise: 7.7
Question:1 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
Then it is known that,
Therefore,
Question:2 Integrate the functions in Exercises 1 to 9.
Answer:
Given function to integrate
Now we can rewrite as
As we know the integration of this form is
Question:3 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:4 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:5 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:6 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
a
And we know that,
Question:7 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:8 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:9 Integrate the functions in Exercises 1 to 9.
Answer:
Given function ,
So, let us consider the function to be;
And we know that,
Question:10 Choose the correct answer in Exercises 10 to 11.
(A)
(B)
(C)
(D)
Answer:
As we know that,
So,
Therefore the correct answer is A.
Question:11 Choose the correct answer in Exercises 10 to 11.
(A)
(B)
(C)
(D)
Answer:
Given integral
So, let us consider the function to be;
And we know that,
Therefore the correct answer is D.
NCERT class 12 maths ch 7 question answer - Exercise:7.8
Question:1 Evaluate the following definite integrals as a limit of sums.
Answer:
We know that,
This is how the integral is evaluated using limit of a sum
Question:2 Evaluate the following definite integrals as limit of sums.
Answer:
We know that
let
Here a = 0, b = 5 and
therefore
Question:3 Evaluate the following definite integrals as limit of sums.
Answer:
We know that
here a = 2 and b = 3 , so h = 1/n
Question:4 Evaluate the following definite integrals as limit of sums.
Answer:
Let
for the second part, we already know the general solution of
So, here a = 1 and b = 4
therefore
So,
Question:5 Evaluate the following definite integrals as limit of sums.
Answer:
let
We know that
Here a =-1, b = 1 and
therefore h = 2/n
By using sum of n terms of GP ....where a = 1st term and r = ratio
.........using
Question:6 Evaluate the following definite integrals as limit of sums.
Answer:
It is known that,
..........................(
)
NCERT class 12 maths ch 7 question answer - Exercise:7.9
Question:1 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:2 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:3 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:4 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:5 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:6 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:7 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:8 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:9 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:10 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:11 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:12 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:13 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:14 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
Multiplying by 5 both in numerator and denominator:
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:15 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
Putting which gives,
As, and as
.
So, we have now:
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:16 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
So, we can rewrite the integral as;
where
. ................(1)
Now, consider
Take numerator
We now equate the coefficients of x and constant term, we get
Now take denominator
Then we have
Then substituting the value of in equation (1), we get
Question:17 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:18 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
can be rewritten as:
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:19 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
can be rewritten as:
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
or we have
Question:20 Evaluate the definite integrals in Exercises 1 to 20.
Answer:
Given integral:
Consider the integral
can be rewritten as:
So, we have the function of ,
Now, by Second fundamental theorem of calculus, we have
Question:21 Choose the correct answer in Exercises 20 and 21.
Answer:
Given definite integral
Consider
we have then the function of x, as
By applying the second fundamental theorem of calculus, we will get
Therefore the correct answer is D.
Question:22 Choose the correct answer in Exercises 21 and 22.
(A)
(B)
(C)
(D)
Answer:
Given definite integral
Consider
Now, putting
we get,
Therefore we have,
we have the function of x , as
So, by applying the second fundamental theorem of calculus, we get
Therefore the correct answer is C.
NCERT solutions for class 12 maths chapter 7 Integrals - Exercise:7.10
Question:1 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
let
when x = 0 then t = 1 and when x =1 then t = 2
Question:2 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
let
when and
using the above substitution we can evaluate the integral as
Question:3 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
let
when x = 0 then and when x = 1 then
Taking as a first function and
as a second function, by using by parts method
Question:4 Evaluate the integrals in Exercises 1 to 8 using substitution.
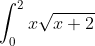 . (Put
. (Put 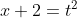 )
)
Answer:
Let
when x = 0 then t = and when x=2 then t = 2
Question:5 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
let
when x=0 then t = 1 and when x= then t = 0
Question:6 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
By adjusting, the denominator can also be written as
Now,
let
when x= 0 then t =-1/2 and when x =2 then t = 3/2
On rationalisation, we get
Question:7 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
the Dr can be written as
and put x+1 = t then dx =dt
when x= -1 then t = 0 and when x = 1 then t = 2
Question:8 Evaluate the integrals in Exercises 1 to 8 using substitution.
Answer:
let
when x = 1 then t = 2 and when x = 2 then t= 4
let
Question:9 Choose the correct answer in Exercises 9 and 10.
(A) 6
(B) 0
(C) 3
(D) 4
Answer:
The value of integral is (A) = 6
let
now, when x = 1/3, t = 8 and when x = 1 , t = 0
therefore
Question:10 Choose the correct answer in Exercises 9 and 10.
(A)
(B)
(C)
(D)
Answer:
The correct answer is (B) =
by using by parts method,
So,
NCERT solutions for class 12 maths chapter 7 Integrals - Exercise:7.11
Question:1 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ............................................................. (i)
By using
We get :-
or
................................................................ (ii)
Adding both (i) and (ii), we get :-
or
or
or
or
Question:2 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have .......................................................................... (i)
By using ,
We get,
or .......................................................(ii)
Adding (i) and (ii), we get,
or
or
Thus
Question:3 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ..................................................................(i)
By using :
We get,
or . ............................................................(ii)
Adding (i) and (ii), we get :
or
or
Thus
Question:4 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ..................................................................(i)
By using :
We get,
or . ............................................................(ii)
Adding (i) and (ii), we get :
or
or
Thus
Question:5 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have,
For opening the modulas we need to define the bracket :
If (x + 2) < 0 then x belongs to (-5, -2). And if (x + 2) > 0 then x belongs to (-2, 5).
So the integral becomes :-
or
This gives
Question:6 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have,
For opening the modulas we need to define the bracket :
If (x - 5) < 0 then x belongs to (2, 5). And if (x - 5) > 0 then x belongs to (5, 8).
So the integral becomes:-
or
This gives
Question:7 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
U sing the property : -
We get : -
or
or
or
or
or
Question:8 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
By using the identity
We get,
or
or
or
or
or
or
Question:9 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
By using the identity
We get :
or
or
or
or
or
Question:10 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
or
or ..............................................................(i)
By using the identity :
We get :
or ....................................................................(ii)
Adding (i) and (ii) we get :-
or
or
Question:11 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
We know that sin 2 x is an even function. i.e., sin 2 (-x) = (-sinx) 2 = sin 2 x.
Also,
So,
or
or
Question:12 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ..........................................................................(i)
By using the identity :-
We get,
or ............................................................................(ii)
Adding both (i) and (ii) we get,
or
or
or
Question:13 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
We know that is an odd function.
So the following property holds here:-
Hence
Question:14 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have
I t is known that :-
If f (2a - x) = f(x)
If f (2a - x) = - f(x)
Now, using the above property
Therefore,
Question:15 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ................................................................(i)
By using the property :-
We get ,
or ......................................................................(ii)
Adding both (i) and (ii), we get
Thus I = 0
Question:16 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have .....................................................................................(i)
By using the property:-
We get,
or
....................................................................(ii)
Adding both (i) and (ii) we get,
or
or
or ........................................................................(iii)
or ........................................................................(iv)
or .....................................................................(v)
Adding (iv) and (v) we get,
Question:17 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have ................................................................................(i)
By using, we get
We get,
.................................................................(ii)
Adding (i) and (ii) we get :
or
or
Question:18 By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.
Answer:
We have,
For opening the modulas we need to define the bracket :
If (x - 1) < 0 then x belongs to (0, 1). And if (x - 1) > 0 then x belongs to (1, 4).
So the integral becomes:-
or
This gives
Question:19 Show that 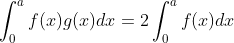 if
if 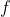 and
and 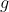 are defined as
are defined as 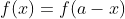 and
and 
Answer:
Let ........................................................(i)
This can also be written as :
or ................................................................(ii)
Adding (i) and (ii), we get,
or
Question:20 Choose the correct answer in Exercises 20 and 21.
(A) 0
(B) 2
(C)
(D) 1
Answer:
We have
This can be written as :
Also if a function is even function then
And if the function is an odd function then :
Using the above property I become:-
or
or
Question:21 Choose the correct answer in Exercises 20 and 21.
Answer:
We have
.................................................................................(i)
By using :
We get,
or .............................................................................(ii)
Adding (i) and (ii), we get:
or
Thus
NCERT solutions for class 12 maths chapter 7 Integrals-Miscellaneous Exercise
Question:1 Integrate the functions in Exercises 1 to 24.
Answer:
Firstly we will simplify the given equation :-
Let
By solving the equation and equating the coefficients of x 2 , x and the constant term, we get
Thus the integral can be written as :
or
Question:2 Integrate the functions in Exercises 1 to 24.
Answer:
At first we will simplify the given expression,
or
Now taking its integral we get,
or
or
Question:3 Integrate the functions in Exercises 1 to 24.
Answer:
Let
Using the above substitution we can write the integral is
or
or
or
or
Question:4 Integrate the functions in Exercises 1 to 24.
Answer:
For the simplifying the expression, we will multiply and dividing it by x -3 .
We then have,
Now, let
Thus,
or
Question:5 Integrate the functions in Exercises 1 to 24.
[Hint:
, put
]
Answer:
Put
We get,
or
or
or
Now put in the above result :
Question:6 Integrate the functions in Exercises 1 to 24.
Answer:
Let us assume that :
Solving the equation and comparing coefficients of x 2 , x and the constant term.
We get,
Thus the equation becomes :
or
or
or
or
Question:7 Integrate the functions in Exercises 1 to 24.
Answer:
We have,
Assume :-
Putting this in above integral :
or
or
or
or
Question:9 Integrate the functions in Exercises 1 to 24.
Answer:
We have the given integral
Assume
So, this substitution gives,
or
Question:10 Integrate the functions in Exercises 1 to 24.
Answer:
We have
Simplifying the given expression, we get :
or
or
or
Thus,
and
Question:11 Integrate the functions in Exercises 1 to 24.
Answer:
For simplifying the given equation, we need to multiply and divide the expression by .
Thus we obtain :
or
or
or
Thus integral becomes :
or
or
Question:12 Integrate the functions in Exercises 1 to 24.
Answer:
Given that to integrate
Let
the required solution is
Question:13 Integrate the functions in Exercises 1 to 24.
Answer:
we have to integrate the following function
Let
using this we can write the integral as
Question:14 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
Let
Now, Using partial differentiation,
Equating the coefficients of and constant value,
A + C = 0 C = -A
B + D = 0 B = -D
4A + C =0 4A = -C
4A = A
A = 0 = C
4B + D = 1 4B – B = 1
B = 1/3 = -D
Putting these values in equation, we have




Question:15 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
(let)
Let
using the above substitution the integral is written as




Question:16Integrate the functions in Exercises 1 to 24.
Answer:
Given the function to be integrated as
Let
Let


Question:17 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
Let
Let f(ax +b) = t ⇒ a .f ' (ax + b)dx = dt
Now we can write the ntegral as
Question:18 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
Let
We know the identity that
sin (A+B) = sin A cos B + cos A sin B










Question:19 Integrate the functions in Exercises 1 to 24.
Answer:
We have
or
or
or
or
or
Thus
Now we will solve I'.
Put x = t 2 .
Differentiating the equation wrt x, we get
Thus
or
Using integration by parts, we get :
or
We know that
Thus it becomes :
So I come to be :-
Question:20 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
= I (let)
Let
using the above substitution we can write the integral as










Question:21 Integrate the functions in Exercises 1 to 24.
Answer:
Given to evaluate





now the integral becomes

Let tan x = f(x)



Question:22 Integrate the functions in Exercises 1 to 24.
Answer:
Given,
using partial fraction we can simplify the integral as
Let
Equating the coefficients of x, x 2 and constant value, we get:
A + C = 1
3A + B + 2C = 1
2A+2B+C =1
Solving these:
A= -2, B=1 and C=3
Question:23 Integrate the functions in Exercises 1 to 24.
Answer:
We have
Let us assume that :
Differentiating wrt x,
Substituting this in the original equation, we get
or
or
Using integration by parts , we get
or
or
Putting all the assumed values back in the expression,
or
Question:24 Integrate the functions in Exercises 1 to 24.
Answer:
Here let's first reduce the log function.
Now, let
So our function in terms if new variable t is :
now let's solve this By using integration by parts
Question:25 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Since, we have multiplied by some function, let's try to make that function in any function and its derivative.Basically we want to use the property,
So,
Here let's use the property
so,
Question:26 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
First, let's convert sin and cos into tan and sec. (because we have a good relation in tan and square of sec,)
Let' divide both numerator and denominator by
Now lets change the variable
the limits will also change since the variable is changing
So, the integration becomes:
Question:27 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Lets first simplify the function.
As we have a good relation in between squares of the tan and square of sec lets try to take our equation there,
AS we can write square of sec in term of tan,
Now let's calculate the integral of the second function, (we already have calculated the first function)
let
here we are changing the variable so we have to calculate the limits of the new variable
when x = 0, t = 2tanx = 2tan(0)=0
when
our function in terms of t is
Hence our total solution of the function is
Question:28 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Here first let convert sin2x as the angle of x ( sinx, and cosx)
Now let's remove the square root form function by making a perfect square inside the square root
Now let
,
since we are changing the variable, limit of integration will change
our function in terms of t :
Question:29 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
First, let's get rid of the square roots from the denominator,
Question:30 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
First let's assume t = cosx - sin x so that (sinx +cosx)dx=dt
So,
Now since we are changing the variable, the new limit of the integration will be,
when x = 0, t = cos0-sin0=1-0=1
when
Now,
Hence our function in terms of t becomes,
Question:31 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Let I =
Here, we can see that if we put sinx = t, then the whole function will convert in term of t with dx being changed to dt.so
Now the important step here is to change the limit of the integration as we are changing the variable.so,
So our function becomes,
Now, let's integrate this by using integration by parts method,
Question:32 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Let I = -(i)
Replacing x with ( -x),
- (ii)
Adding (i) and (ii)
Question:33 Evaluate the definite integrals in Exercises 25 to 33.
Answer:
Given integral
So, we split it in according to intervals they are positive or negative.
Now,
as
is positive in the given x -range
Therefore,
as
is in the given x -range
and
in the range
Therefore,
as
is in the given x -range
and
in the range
Therefore,
So, We have the sum
Question:34 Prove the following (Exercises 34 to 39)
.
Answer:
L.H.S =
We can write the numerator as [(x+1) -x]
= RHS
Hence proved.
Question:35 Prove the following (Exercises 34 to 39)
Answer:
Integrating I by parts
Applying Limits from 0 to 1
Hence proved I = 1
Question:36 Prove the following (Exercises 34 to 39)
Answer:
The Integrand g(x) therefore is an odd function and therefore
Question:37 Prove the following (Exercises 34 to 39)
Answer:
For I 2 let cosx=t, -sinxdx=dt
The limits change to 0 and 1
I 1 -I 2 =2/3
Hence proved.
Question:38 Prove the following (Exercises 34 to 39)
Answer:
The integral is written as
Hence Proved
Question:39 Prove the following (Exercises 34 to 39)\
Answer:
Integrating by parts we get
For I 2 take 1-x 2 = t 2 , -xdx=tdt
Hence Proved
Question:40 Evaluate as a limit of a sum.
Answer:
As we know
where b-a=hn
In the given problem b=1, a=0 and
Question:41 Choose the correct answers in Exercises 41 to 44.
(A)
(B)
(C)
(D)
Answer:
the above integral can be re arranged as
let e x =t, e x dx=dt
(A) is correct
Question:42âââââââ Choose the correct answers in Exercises 41 to 44.
(A)
(B)
(C)
(D)
Answer:
cos2x=cos 2 x-sin 2 x
let sinx+cosx=t,(cosx-sinx)dx=dt
hence the given integral can be written as
B is correct
Question:43âââââââ Choose the correct answers in Exercises 41 to 44.
(A)
(B)
(C)
(D)
Answer:
As we know
Using the above property we can write the integral as
Answer (D) is correct
Question:44 Choose the correct answers in Exercises 41 to 44.
(A) 1
(B) 0
(C) -1
(D)
Answer:
as
Now the integral can be written as
(B) is correct.
If you are looking for integrals class 12 NCERT solutions of exercises then they are listed below.
- Integration Class 12 Exercise 7.1
- Integration Class 12 Exercise 7.2
- Integration Class 12 Exercise 7.3
- Integration Class 12 Exercise 7.4
- Integration Class 12 Exercise 7.5
- Integration Class 12 Exercise 7.6
- Integration Class 12 Exercise 7.7
- Integration Class 12 Exercise 7.8
- Integration Class 12 Exercise 7.9
- Integration Class 12 Exercise 7.10
- Integration Class 12 Exercise 7.11
- Integration Class 12 Miscellaneous Exercise
About NCERT solutions for class 12 maths chapter 7 integrals
The word integration literally means summation. When you have to find the sum of finite numbers you can do by simply adding these numbers. But when you are finding the sum of a certain number of elements as the number of elements tends to infinity and at the same time each term becomes infinitesimally small, you can use a prosses to find its limit called integration.
Integrals has 13 % weightage in 12 board final examinations. Next chapter "applications of integrals" is also dependent on this chapter. So you should try to solve every problem of this chapter on your own. If you are not able to do, you can take the help of these NCERT solutions for class 12 maths chapter 7 integrals. In this chapter, there are 11 exercises with 227 questions and also 44 questions are there in miscellaneous exercise. Here, the NCERT solutions for class 12 maths chapter 7 integrals are solved and explained in detail to develop a grip on the topic. Here, you will learn two types of integrals: Definite integral and Indefinite integral and also learn their properties and formulas.
Definite Integral | Indefinite Integral | |
Definition | A definite Integral has upper and lower limits if 'a' and 'b' are the limits or boundaries. The definite integral of f(x) is a number, not function . | An integral without upper limit and lower limit. It is also an antiderivative. The indefinite integral of f(x) is a function not number. |
Expression | |
NCERT Solutions for Class 12 Maths Chapter 7 Integrals - Topics
7.1 Introduction
7.2 Integration as an Inverse Process of Differentiation
7.2.1 Geometrical interpretation of indefinite integral
7.2.2 Some properties of indefinite integral
7.2.3 Comparison between differentiation and integration
7.3 Methods of Integration
7.3.1 Integration by substitution
7.3.2 Integration using trigonometric identities
7.4 Integrals of Some Particular Functions
7.5 Integration by Partial Fractions
7.6 Integration by Parts
7.7 Definite Integral
7.7.1 Definite integral as the limit of a sum
7.8 Fundamental Theorem of Calculus
7.8.1 Area function
7.8.2 First fundamental theorem of integral calculus
7.8.3 Second fundamental theorem of integral calculus
7.9 Evaluation of Definite Integrals by Substitution
7.10 Some Properties of Definite Integral
NCERT solutions for class 12 maths - Chapter wise
| Chapter 1 | Relations and Functions |
| Chapter 2 | Inverse Trigonometric Functions |
| Chapter 3 | Matrices |
| Chapter 4 | Determinants |
| Chapter 5 | Continuity and Differentiability |
| Chapter 6 | Application of Derivatives |
| Chapter 7 | Integrals |
| Chapter 8 | Application of Integrals |
| Chapter 9 | Differential Equations |
| Chapter 10 | Vector Algebra |
| Chapter 11 | Three Dimensional Geometry |
| Chapter 12 | Linear Programming |
| Chapter 13 | Probability |
Key Features of NCERT Solutions for Class 12 Maths Chapter 7 Integrals
The NCERT chapter 7 class 12 maths offers several key features to aid students in their understanding and mastery of this topic. Some of these features include
Detailed explanation: The chapter 7 class 12th maths solutions provide a comprehensive and in-depth explanation of the concepts of integrals, making it easier for students to grasp the subject.
Step-by-Step Solutions: The integration class 12 ncert solutions break down complex problems into simpler steps, making it easier for students to follow and understand the process.
Clear Diagrams: The integrals class 12 solutions make use of clear and informative diagrams to help students visualize the concepts, making it easier for them to comprehend the material.
Plenty of Practice Problems: The ch 7 maths class 12 include a large number of practice problems to help students strengthen their knowledge and skills.
Accurate answers: The class 12 ch 7 maths ncert solutions are checked and verified by experts to ensure accuracy, helping students avoid mistakes and improve their grades.
Also read,
- NCERT Exemplar Class 12 Chemistry Solutions
- NCERT Exemplar Class 12 Mathematics Solutions
- NCERT Exemplar Class 12 Biology Solutions
- NCERT Exemplar Class 12 Physics Solutions
SAT® | CollegeBoard
Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing
TOEFL ® Registrations 2024
Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!
More about NCERT Solutions for Class 12 Maths Chapter 7 Integrals
The word integration literally means summation. When you have to find the sum of finite numbers you can do by simply adding these numbers. But when you are finding the sum of a certain number of elements as the number of elements tends to infinity and at the same time each term becomes infinitesimally small, you can use a prosses to find its limit called integration.
Integrals have 13 % weightage in 12 board final examinations. Next chapter "applications of integrals" is also dependent on this chapter. So you should try to solve every problem of this chapter on your own.
If you are not able to, you can take the help of these NCERT solutions for class 12 maths chapter 7 integrals.
In this NCERT Class 12 Maths solutions chapter 7, there are 11 exercises with 227 questions and also 44 questions are there in miscellaneous exercises. Here, the Class 12 Maths Chapter 7 NCERT solutions are solved and explained in detail to develop a grip on the topic.
NCERT solutions for class 12 - subject wise
- NCERT solutions for class 12 mathematics
- NCERT solutions class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
How to use NCERT solutions for class 12 maths chapter 7 Integrals
You are expected to remember all formulas of differentiation, and then can start with basic integration
Try to relate differentiation formulas with integrations formulas because it will help you to remember all the integration formulas
When you are done with basic integration, you should learn different methods of integration for different types of functions. If you find difficulties in learning the method you should learn one method at a time to solve a particular type of problem
After learning the different methods of integration, you should be able to determine which method will be used to solve a particular type of problem
When you become good with indefinite integrals, move to the definite integrals and learn some properties to solve definite integrals. NCERT Class 12 Maths solutions chapter 7 integrals will help you for the same
This chapter requires a lot of practice. First, solve all the NCERT textbook questions, then, you can take the help of NCERT solutions for class 12 maths chapter 7 integrals.
If you have solved all NCERT questions, you can solve CBSE previous year papers also to get familiar with the type of questions which are asked in previous years.
NCERT solutions class 12 maths chapter 12 pdf download will be made available soon. Till then you can save the webpage and practice these solutions offline.
NCERT Books and NCERT Syllabus
Frequently Asked Question (FAQs)
Students consider Integration which is integrals and applications of integration are the most difficult chapter in CBSE class 12 maths but with the regular practice of NCERT problems you will be able to have a strong grip on this chapter also. it's true that there is no substitute for hard work but the right strategy and quality study material are also essential to get command of this chapter, therefore, NCERT exercises are recommended for practice.
NCERT solutions are created by the expert team of careers360 who know how best to write answers in the board exam in order to get good marks. Integrating their techniques can benefit in obtaining meritorious marks. Sometimes students do not understand where s/he are making a mistake, NCERT solutions can help them to understand that. the practice of a lot of questions and their solution make you confident and help you in getting an in-depth understanding of concepts. Therefore NCERT solutions are very helpful for students.
Integrals have 13 % weightage in CBSE class 12th board final examination. having 13% weightage, Integral become very students for CBSE aspirant but it demand lot of practice. Interested students can refer to integrals class 12 solutions.
The NCERT Solutions for maths ch 7 maths class 12 is not complicated to understand. It is a fascinating topic in Class 12 that is also relevant at higher education levels. A solid understanding of integral formulas will enable students to solve integration problems effectively. A thorough knowledge of derivatives is crucial for comprehending the concepts of integral calculus with ease. For ease, students can study integrals class 12 ncert solutions pdf both online and offline.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
Hello aspirant,
The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.
There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.
https://www.careers360.com/courses/graphic-designing-course
Thank you
Hope this information helps you.
hello,
Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.
I hope this was helpful!
Good Luck
Hello dear,
If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.
As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.
Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.
Believe in Yourself! You can make anything happen
All the very best.
Hello Student,
I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.
You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.
All the best.
Hi,
You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.
Popular CBSE Class 12th Questions
Colleges After 12th
Also Read
Applications for Admissions are open.

JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
ApplyRanked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
ApplyEnrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ApplyStart your JEE preparation with ALLEN